基于模拟退火的粒子群算法的船舶空调系统能耗优化研究

曾 建，杨祥国，刘自然，荣晨光

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

船舶在不同海域航行时，为了保证船员工作生活环境的舒适性，都会设有空调系统，以维持舱室内空气温湿度的稳定[1]，但同时也为船舶带来了较大的能耗问题，因此对于中央空调系统开展性能优化研究对船舶实现节能减排具有非常重要的意义。文献[2]通过对不同分区的空调设备启停控制来达到节能的效果，但未对系统的运行参数进行优化；文献[3]以系统总能耗为优化目标，得到不同负荷下的最佳工况点，但是仅考虑了部件的物理约束；文献[4]仅对水系统各个部件的节能特性进行了研究，没有考虑风系统对空调系统能耗的影响。针对中央空调系统强耦合性的特点，要实现中央空调系统总能耗最低的目标，必须统一考虑系统与各部件之间的关联与耦合。因此本文提出一种基于模拟退火的粒子群优化算法，对系统的运行参数进行优化，保证系统的最佳运行。

1 基于模拟退火的粒子群优化算法

1.1 粒子群算法

粒子群算法是一种基于群体的智能优化算法。在粒子群算法中，每个粒子(Particle)看作优化问题的解，在迭代过程中根据适应度(Fitness Value)来更新个体最优位置点pXibest与种群最优位置点gXbest，然后粒子更新自己的速度与位置，进行下一次迭代寻优。

粒子的速度和位置信息根据公式(1)、(2)来更新：

pvi,j(t+1)=ωvi,j(t)+c1r1[pxi,jbest-pxi,j(t)]+c2r2[gxi,jbest-pxi,j(t)]，

(1)

pxi,j(t+1)=pxi,j(t)+pvi,j(t) ,

(2)

式中，t为迭代次数，r1、r2为均匀分布在[0，1]之间的随机数，c1、c2为算法学习因子，ω为惯性权重参数，pxi,j、pvi,j分别为粒子当前的位置与速度，pxi,jbest、gxi,jbest分别为粒子与种群当前的最优位置 。

本文采用一种非线性调整惯性权重的粒子群算法(ULωPSO)，该算法利用指数函数y=ex，其中x∈[-∞,0]，来非线性地调整惯性权重的下降。惯性权重参数ω的计算如公式(3)所示：

(3)

式中，tmax为最大迭代次数，ωmax和ωmin分别为惯性权重参数的最大值与最小值。

粒子群算法主要依靠群体间的竞争与合作，所以在运行的初始阶段，算法的收敛速度较快，但粒子群算法存在易陷入局部最优、精度较低等缺点。

1.2 模拟退火算法

模拟退火算法是根据固体退火的热力学原理，并广泛应用于解决组合优化问题的算法。算法在优化过程中，首先确定初始温度，随机选择一个初始状态并进行评估；对当前状态添加一个小扰动，重新评估该状态的目标函数值，以1的概率接收较好的值，以概率k接受一个较差的值并更新状态，通过迭代直到算法冷却。

模拟退火算法具有渐进收敛性，只要初始温度T0足够高，退火流程足够慢，该算法理论上会以100%的概率收敛到全局最优解。但是搜索空间较大时，需要花费较长的迭代时间才能够收敛得到一个高质量的近似最优解，收敛速度慢，不满足大规模实际问题的应用需求。

1.3 基于模拟退火的粒子群优化算法

针对粒子群算法与模拟退火算法各自的特点，本文提出了一种基于模拟退火的粒子群算法(SA-ULωPSO)，其将Metropolis准则中的粒子取舍机制引入到非线性惯性权重粒子群算法(ULωPSO)中，不仅保持了粒子群算法收敛速度快的优点，同时还改善了算法早熟收敛问题，增加了搜索的多样性。

基于模拟退火的粒子群算法的寻优步骤如下。

1)设定粒子的个数N，初始化粒子的位置pXi和速度pVi、设定最大迭代次数tmax、惯性权重参数ω、初始温度T0、降温系数φ以及允许变坏的范围β。

2)初始化个体最优位置pXibest、种群最优位置gXbest、个体最优值pFibest以及种群最优值gFbest。

3)计算微粒的适应度，通过比较更新pXibest、gXbest、pFibest以及gFbest。

4)根据公式(1)～(2)，更新粒子的速度与位置。

5)计算粒子位置更新后的适应度变化量Δf=f(pNxi,j)-f(pxi,j)，pNxi,j为更新后的粒子位置，如果Δf<β，则更新种群最优位置;否则，计算k=exp(-Δf/T)，T为退火温度，若k大于在[0,1]中选取的任何一个随机数，则更新种群最优位置；否则，保持原先的位置与速度不变。

6)如果迭代达到最大次数tmax或者达到预期精度，算法收敛，当前gXbest和gFbest就是最终结果；否则更新惯性权重参数ω、退火温度T以及迭代次数t，返回步骤3)，算法继续，直到满足终止条件。

2 中央空调系统优化模型的建立

本文以某海洋平台工作区中央空调系统为研究对象，空调面积844 m2，冷水机组2台(一用一备)，额定制冷量为210 kW 。中央空调系统结构示意图如图1所示。

2.1 优化目标函数的建立

中央空调系统的主要能耗设备包括冷水机组、冷冻水泵、冷却水泵、空调机组风机，即：

Ptotal=Pchiller+Pchwp+Pcwp+Pcfan，

(4)

式中，Ptotal为中央空调系统总能耗，Pchiller为冷水机组能耗，Pchwp为冷冻水泵能耗，Pcwp为冷却水泵能耗，Pcfan为空调机组能耗。

各设备的能耗表示如下：

(5)

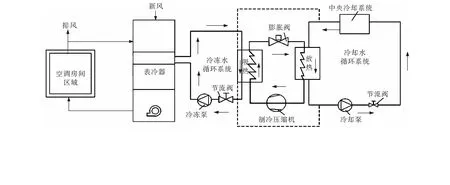
图1 中央空调系统结构示意图

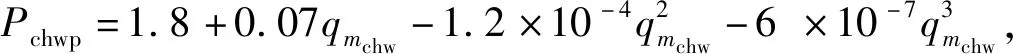
(6)

(7)

(8)

式中，Tchwo为冷冻水供水温度，Tcwi为冷却水供水温度，qmchw、qmcw分别为冷冻水和冷却水流量，qvf为风机流量 。

综合考虑各设备运行特性和设备间耦合关系，确定中央空调系统的优化变量，包括冷冻水供水温度、冷冻水流量、冷却水流量、空调机组风量、空气湿球温度和冷负荷。

2.2 约束条件的确定

中央空调系统具有强耦合性，因此优化模型的约束条件不仅包括设备本身的物理约束，还包括设备之间的相互约束。

1)冷水机组的进出水温约束。

Tchwo,min≤Tchwo≤Tchwo,max。

(9)

2)冷冻水与冷却水流量的约束。

qmchw,min≤qmchw≤qmchw,max，

(10)

qmcw,min≤qmcw≤qmcw,max。

(11)

3)空调机组风机流量的约束。

qvf,min≤qvf≤qvf,max。

(12)

4)空调机组与冷冻水泵之间的约束。

(13)

式中，Qa为空调机组实际供冷量，Qa,0为空调机组额定供冷量，Twb为实际空气湿球温度，Twb,0为额定空气湿球温度，Tchwo,0为冷冻水额定供水温度，qmchw,0为冷冻水额定流量，qvf,0为空调机组额定风机流量。

5)冷水机组与冷冻水泵，冷却水泵相互之间的约束。

Qchiller=qmchwcw(Tchwo-Tcwi)，

(14)

Pchiller+Qchiller=qmcwcw(Tcwi-Tchwo)，

(15)

式中，Qchiller为冷水机组供冷量，cw为水的比热容。

由此得到中央空调系统优化的约束条件如下：

(16)

3 仿真与分析

基于前文建立的中央空调系统能耗优化模型，运用基于模拟退火的粒子群算法和非线性惯性权重粒子群算法分别对系统进行参数优化，比较分析不同工况下2种算法的节能效果。

3.1 不同负荷情况下的优化分析

设定冷负荷为额定负荷的70%，空气湿球温度为25 ℃，分别运用2种算法对中央空调系统参数进行优化，并对比结果。SA-ULωPSO算法的设定参数如表1所示,ULωPSO算法除缺少β、T0、φ这3个参数外，其余参数与SA-ULωPSO算法参数一致。

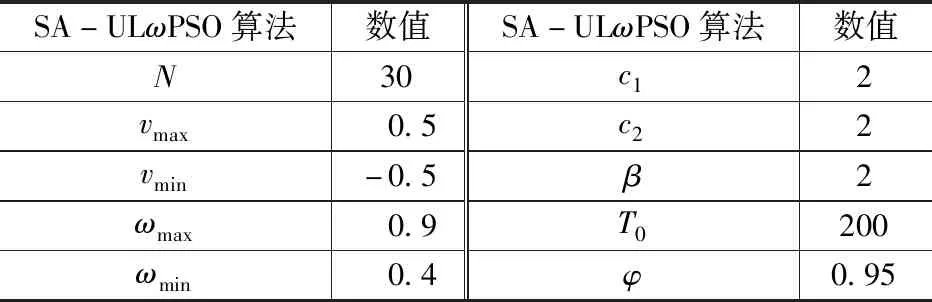
表1 SA-ULωPSO算法的设定参数

设定最大迭代次数为200次，得到负荷率70%时，2种算法对空调系统参数的优化对比如图2所示。由图2可知，利用SA-ULωPSO算法进行优化时，当迭代次数达到39时算法收敛，此时的能耗为52.15 kW;利用ULωPSO算法进行优化时，当迭代次数达到61时算法收敛，此时的能耗为54.04 kW，因此可知SA-ULωPSO算法的收敛速度和收敛精度都优于ULωPSO算法。

图2 负荷率70%时，2种算法对空调系统参数的优化对比

设定负荷为90%时，2种算法对空调系统参数的优化对比如图3所示。由图3可知，利用SA-ULωPSO算法进行优化时，当迭代次数达到42次时，算法收敛，此时的能耗为66.44 kW;利用ULωPSO算法进行优化时，当迭代次数达到63次时，算法收敛，此时的能耗为70.23 kW。

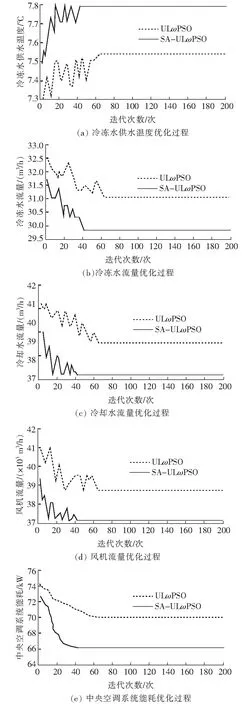
图3 负荷率90%时，2种算法对空调系统参数优化对比

3.2 一个制冷周期的优化分析

本文选取7月份某日的空调系统运行数据，对提出的算法进行仿真验证，当日冷负荷与空气湿球温度变化曲线如图4、图5所示，并将其作为优化模型的输入。

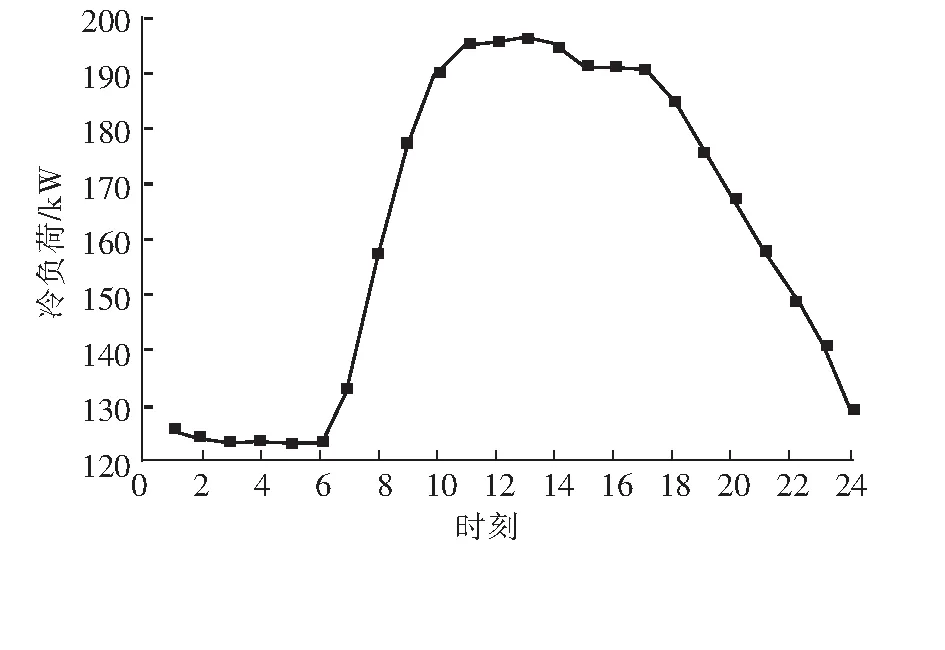
图4 冷负荷变化曲线

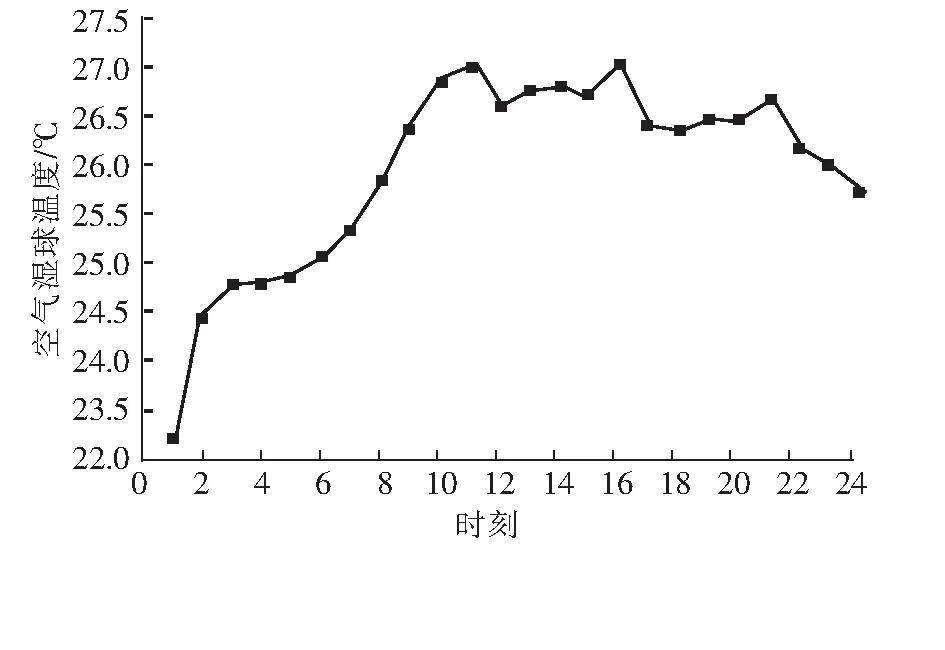
图5 空气湿球温度变化曲线

在一个制冷周期内，房间的冷负荷是不断变化的，因此空调系统的工况点也会随之不断变化，分别采用2种算法对空调参数进行优化，得到优化后的中央空调系统总能耗对比如图6所示。由图6可知，8时之前与19时之后，系统冷负荷较小，因此空调优化前后总能耗相差较大，而在8时到19时之间，由于室外温度与湿度的提高，使得系统的负荷增大，优化前后能耗差别不大，说明算法优化的系统节能率随着负荷的变大而减小。表2为空调系统各设备的能耗对比，其中冷水机组和空调机组的节能率较大，这是因为冷冻水供水温度提升后，使得冷水机组的蒸发效率提高，因而提高了机组的能耗比，最终系统总节能率为9.07%，优化节能效果良好。

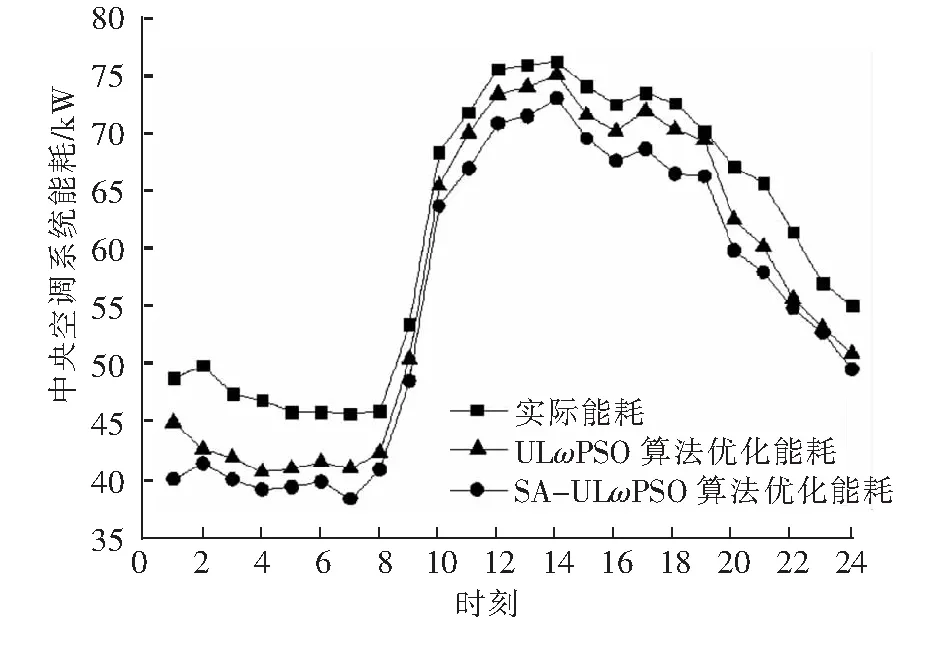
图6 优化后的中央空调系统总能耗对比

表2 空调系统各设备能耗对比 kW

4 结束语

本文提出一种基于模拟退火的粒子群算法，以中央空调系统总能耗为目标函数，建立中央空调系统的优化模型，分别运用基于模拟退火的粒子群算法和非线性惯性权重粒子群算法对中央空调系统优化模型进行参数优化，通过对不同工况下2种算法的收敛速度与能耗比较，表明本文设计的基于模拟退火算法的粒子群算法在收敛速度和节能效果上都有明显优势。