压缩气流灭弧条件下配网线路雷击跳闸率计算

张奇星，李籽剑，张强

(1.广西大学 电气工程学院，南宁 530000； 2.国网湖北省电力有限公司电力科学研究院，武汉 430000；3.武汉地铁资源经营有限公司，武汉 430000)

0 引 言

随着我国电网的系统化规模化，电网停电事故将严重影响国民经济，甚至造成人身安全，秩序混乱的现象。根据电网故障数据统计显示，我国电网雷击事故高达40%～70%，因此如何有效降低雷击跳闸率成为电力系统安全的重大研究课题[1-4]。

传统的防雷方法是以抑制绝缘子闪络为目的，具体有架设避雷线、加强绝缘、降低接地电阻等方法。但是由于受雷击强度、雷击类型、地形气候等自然不可控因素的影响，导致耐雷水平不达标，雷击跳闸率居高不下的现状[5-8]。

压缩灭弧防雷技术是一种全新的防雷方法，它以抑制电力系统系统在雷击条件下绝缘子旁路闪络通道里形成的工频短路电弧为目的，在泄放巨大雷电能量的同时又阻断了工频建弧通道，实现了防雷效果与雷击强度、雷击方式、雷击部位、地形气候等自然因素无关[9]。其基本原理是利用灭弧结构的特殊排列形式，将电弧分为多个断点，并在每个灭弧单元中将电弧冷却压缩形成轴向压力梯度，进而产生自膨胀气流。气流与电弧完成瞬时传热，最终通过温升爆炸的方式向外喷射电弧与气流的混合体。研究表明这种伴随性的熄弧过程将实现电弧建立与熄灭的同步性，且在多断点的特殊结构下，电弧的发展得到了进一步抑制。文献[10-14]中详细介绍了压缩灭弧防雷器的原理并进行了仿真，结果表明冲击电弧电流在灭弧管道内受到了深度抑制，在冲击电弧与工频电弧解耦时后，工频电弧难以发展，最终熄灭[10-14]。本文以压缩气流灭弧防雷间隙的灭弧实验数据为基础，通过搭建雷击跳闸率数学计算模型，分析了压缩气流灭弧防雷间隙对雷击跳闸率的影响。最后通过算例和实际运行情况验证了压缩气流灭弧防雷间隙的有效降低雷击跳闸率。

1 压缩气流灭弧防雷间隙对绝缘子的有效保护系数

压缩气流灭弧防雷间隙是一种带有灭弧功能的并联间隙，因此其本质上仍然属于安装在绝缘子旁路的并联保护间隙。当绝缘子两侧出现雷击过电压波时，必须保证并联间隙的击穿放电电压小于绝缘子串闪络电压，因此可定义灭弧防雷间隙的有效保护系数为出现在线路电压时，并联间隙被击穿且绝缘子不发生闪络的概率。

由于间隙击穿与电压波形与间隙结构等因素有关，因此，气体击穿具有分散性和统计性，根据研究表明空气间隙的击穿放电电压服从正态分布[12]，其击穿电压概率密度函数为：

(1)

式中u50%为间隙击穿概率为50%时的峰值电压；σ0为标准偏差。为了便于计算，可设：

(2)

式中σ被称为击穿概率的变异系数，其值与电压波形和间隙类型有关。实验表明，雷击冲击电压的变异系数可取3%。因此设绝缘子沿面闪络电压为Ua，灭弧装置空气主间隙击穿电压为Ub，则两者分别满足正态分布：

(3)

式中Ua50%和Ub50%分别表示绝缘子和灭弧装置空气间隙的50%击穿放电电压。实验表明雷电冲击电压作用下空气间隙的击穿电压与间隙保持较好的线性关系，因此设灭弧装置空气主间隙长度占绝缘子绝缘距离的λ倍，该值同时也为灭弧装置的绝缘配合比，可得：

Ub=λUa

(4)

为了保证绝缘子得到有效保护，则需保证灭弧装置空气主间隙击穿电压为Ub小于绝缘子沿面闪络电压为Ua。令U=Ua-Ub，根据概率与数理统计知识可知，U仍然满足正态分布，其期望为Ua50%-Ub50%，方差为(0.03Ua50%)2+(0.03Ub50%)2。联立式(4)，经标准化后可得：

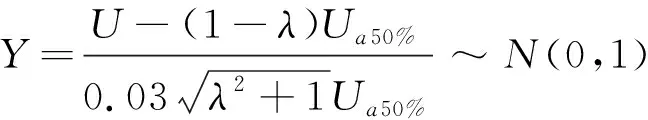
(5)

因此，可知灭弧装置有效保护绝缘子的保护系数Pm为：

(6)

通过查询标准正态分布表可知，在λ小于等于0.85时，保护系数Pm为99.993%，几乎可实现雷击过电压波百分之百优先击穿防雷间隙，由于雷击过电压击穿间隙的分散性较大，为了有效保护绝缘子，理应留有一定的裕度，但考虑系统可能出现的内部过电压导致间隙击穿的现象，裕度不易取过大，因此λ取值可在0.75～0.85之间，此时的保护系数Pm大于等于99.993%。

2 压缩气流灭弧防雷间隙下的建弧率计算

2.1 无灭弧装置下的建弧率

当绝缘子两侧出现雷击过电压波时，绝缘子旁路会形成闪络通道，系统将借此通道形成工频电弧的概率即为建弧率，其值可表示为：

η0=(4.5E0.75-14)%

(7)

式中E为绝缘子两端的平均工作场强。在配网系统中，在变压器端常采用中性点非有效接地，因此其工作场强可表示为：

(8)

式中Un为系统标称电压；l为绝缘子串长度。

2.2 含灭弧装置下的建弧率

根据式(7)、式(8)可得配网线路在常规情况不做其他处理时的建弧率，当配网系统某处建弧成功，则会引起工频短路故障，引起线路跳闸。对于输配网系统而言，继电保护最快动作时间为10 ms～20 ms[13]，如果压缩气流灭弧防雷间隙在继电保护最快动作时间内完成有效熄弧可认为灭弧成功，线路不建弧。因此可定义灭弧系数为灭弧装置在继电保护最快动作时间内熄灭电弧的概率。将灭弧系数修正原有线路的建弧率则可得含灭弧装置下的建弧率。

灭弧装置的灭弧性能与灭弧管道结构和工频电弧电流大小等因素有关，导致灭弧时间具有一定的分散性，因此可利用统计学知识计算灭弧时间的概率分布。假设在同一工频电弧电流幅值下灭弧时间满足高斯分布，其概率分布函数为：

(9)

式中t0为灭弧时间的期望值;σ为灭弧时间的标准差，此二值均为未知参数，因此我们可通过数理统计方式求解此二值，从而求得灭弧时间的概率分布函数。假设多次重复实验中灭弧时间所有可能的观察值为总体，总体所对应的随机变量T，则有T～N(t0，σ2)，可利用最大似然估计法对t0及σ进行参数估计。取随机样本t1，t2，…，tn，它们均来自随机变量T且相互独立，建立似然函数为:

(10)

根据求解似然函数，令：

(11)

由式(11)可解得t0与σ的估计值：

(12)

基于上述理论计算灭弧时间的概率分布，需要对总体进行多次重复性试验，选取试验样本。实验中分别选定了三组不同工频电流幅值的情况下进行重复试验，其灭弧实验效果图如图1所示。

图1 高速摄像机拍摄记录的灭弧过程Fig.1 Arc extinction process of high speed camera recording

每组实验各100次，并记录了对应灭弧时间出现的次数，其实验数据如表1所示。

在每组工频电流幅值的实验中随机选取的100个样本代入式(12)即可以求得t0和σ的估计值，如表2所示。

表2 不同工频电弧电流下参数估计值Tab.2 Parameter estimates for different power frequency arc currents

由此便可得到指定工频电弧电流下的灭弧时间的概率分布函数。如前所述，当灭弧时间小于继电保护时间时，可认为建弧失败，因此灭弧系数为：

(13)

根据式(13)可通过查表确定灭弧系数，表3记录了每组实验的灭弧系数。

表3 不同工频电弧电流下灭弧系数Tab.3 Arc extinguishing coefficient under different power frequency arc currents

由此可以得出压缩气流灭弧防雷间隙保护下的配网建弧率为：

η=(1-M)η0

(14)

3 压缩气流灭弧防雷间隙下的雷击跳闸率计算

3.1 反击时的雷击跳闸率计算

为评估配网防雷效果，需要把线路长度和雷暴日数换算到同一条件下进行分析比较，因此引入雷击跳闸率这一概念，它是指在40个雷暴日下，100 km线路每年因遭受雷击而引起的跳闸次数[14]。设N为每100 km线路遭受雷击次数，则有：

(15)

式中b为两避雷线间的距离；hb为避雷线的平均高度；γ为落雷密度，其值与雷暴日Td有关，经换算后可化简式(15)得：

N=0.28(b+4hb)

(16)

当雷击杆塔时对线路形成反击，则含灭弧装置的反击耐雷水平为：

(17)

式中k0为避雷线与输电线的几何耦合系数；k为乘以电晕影响后的修正系数；β为避雷线的分流系数；R为冲击接地电阻；Lgt为杆塔总电感；hd、ha、hgt代表导线平均高度、横搭高度、杆塔高度。

设P1为出现超过反击耐雷水平的雷电流的概率，其表达式根据国家标准有：

(18)

当雷击杆塔(设击杆率为g)且雷电流幅值大于反击耐雷水平，则在灭弧装置主间隙上就会形成闪络通道，如若灭弧装置未在继电保护最快动作时间内熄弧，则会引起则会发生雷击跳闸，因此反击时的雷击跳闸率为：

n1=NgηP1Pm

(19)

3.2 绕击时的雷击跳闸率计算

由于失去了避雷线的耦合分流作用，绕击时的耐雷水平将远小于反击，其表达式为：

(20)

目前分析绕击闪络率的方法有很多，包括有规程法、电气几何模型法、先导发展模型发和绕击概率模型法[15-18]。本文运用电气几何模型法中的暴露距离[19]计算绕击闪络率。根据Glode提出的击距公式[20]为：

r=3.3I0.78

(21)

且由于配网线路电压等级低，其击距系数可取1(大地的击距与导线或避雷线的击距相等)，根据电气几何模型可求出最大击距为：

(22)

式中α为避雷线保护角；F=1-sin2α，G=F[(hd-hb)/cosα]2。再根据杆塔类型等建立电气几何模型，其绕击闪络率公式为：

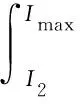
(23)

式中γ取0.07；Z为暴露距离；f(I)为雷电流幅值的概率密度函数，其表达式可根据式(18)求得：

(24)

由于此处绕击闪络率代表在雷暴日为40 d下，每年每100 km的闪络次数。因此其绕击跳闸率应为：

(25)

因此安装压缩气流灭弧装置下的雷击跳闸率为：

n=n1+n2

(26)

4 算例分析

如图2为某地双电源的配网系统图。

图2 某地配网系统图Fig.2 Distribution network system

图2中左侧为发电机为G1，其输送容量为90 MV·A，负序阻抗与次暂态电抗均为0.15。图右侧右发电机为G2，输送容量为50 MV·A，次暂态电抗为0.27，负序阻抗为0.45。母线BUS1、BUS4的电压等级为10 kV，BUS2、BUS3电压等级为35 kV。图左变压器为T1，其接线方式为Δ/Y接法，二次端中性点接地阻抗为26 Ω，其输送容量为100 MV·A，短路电压为10.5。右图变压器T2接线方式Y/Δ，其为其输送容量为60 MV·A，短路电压为10.5。母线BUS2到BUS3由双回输电线路连接，其长度为50 km，且其阻抗为0.4 Ω/km，零序阻抗为正序阻抗的三倍。在35 kV母线附近的杆塔模型如图3所示，由于该线路处在变电所进线段，因此采取假设单根避雷线的方式，避雷线半径为2 mm，其弧垂为1.8 m，杆塔上的冲击接地电阻为10 Ω。线路绝缘子采用3片XWP-7型，其每片长度为146 mm，百分之五十放电电压为350 kV，绝缘子旁路装设压缩气流灭弧防雷装置，绝缘子下方导线的弧垂为3 m。试计算变压器G1进线段的母线BUS2附近的雷击跳闸率。

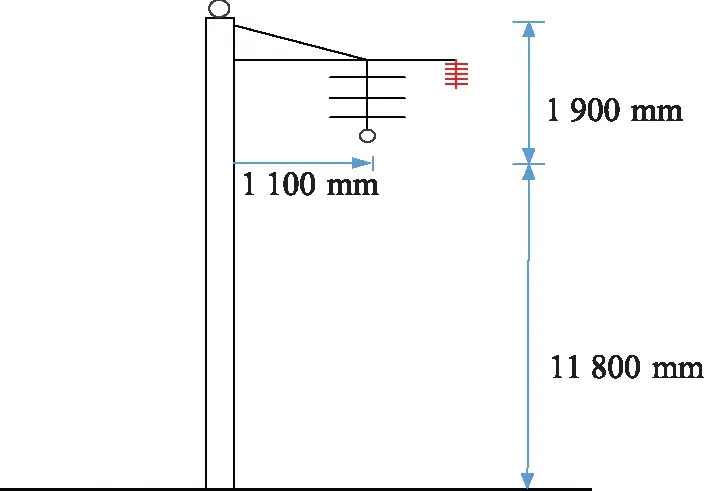
图3 杆塔示意图Fig.3 Tower schematic diagram

4.1 工频电弧电流值及灭弧系数的计算

为了计算线路上的建弧率，首先要计算工频短路电流，假设母线BUS2附近的杆塔因雷击发生单相短路故障，取系统基准容量SB=100 MV·A，35 kV、10 kV电压等级的线路及母线上的平均电压Vav为37 kV、10.5 kV，取系统基准电压VB=Vav。

(1)元件参数的标幺值计算。

发电机：

变压器：

输电线路：

(2)序网络的绘制。

由于正序和负序网络不包含中性点接地阻抗，因此可根据上面计算所得各元件的阻抗值绘制网络图。而零序网络中，从短路点左侧看的T1为Y型中性点经接地阻抗Xn接地，因此3倍的接地阻抗Xn应串连入回路中；短路点右侧看T2为Y型中性点不接地，因此可作开路处理。由此可得到序网络如图4所示。

图4 序网络图Fig.4 Sequence network diagram

根据图4可得各序组合阻抗为：

X1∑=(0.167+0.105)//(0.73+0.175+0.54)=0.229

X2∑=(0.167+0.105)//(0.73+0.175+0.9)=0.236

X0∑=0.105+5.697=5.802

(3)单相接地短路计算。

故障相的正序电流为：

短路点短路电流的有名值：

由此可得短路点的工频电弧电流幅值为0.749 kA。根据第二章的实验计算数据可知此时的灭弧系数为0.999 2。

4.2 建弧率计算

本文选定的线路电压等级为35 kV，其变电所变压器中性点一般采取非有效接地的方式，则绝缘子附近电场强度可根据式(8)得：

则根据式(7)和式(14)可得：

η=(1-0.9992)×(4.5×400.75-14)%=0.05%

4.3 耐雷水平计算

(1)反击耐雷水平计算。

根据图3的杆塔模型可计算出导线及避雷线的平均高度hd、hb为：

单根避雷线对导线的几何耦合系数k0为：

取电晕后的耦合修正系数k1为1.15，则修正后的耦合系数为k为0.141 3。杆塔电感Lgt经计算为11.508 μH，分流系数β为0.9，冲击接地电阻R为10 Ω，则根据式(17)得反击耐雷水平I1为21.399 5 kA。根据式(18)可计算超过反击耐雷水平的概率P1为0.571 2。

(2)绕击耐雷水平计算。

根据式(20)可得出绕击的耐雷水平I2等于2.975 kA。

4.4 电气几何模型法分析绕击闪络率

利用暴露距离的方法计算绕击闪络率。根据式(22)可求得临界击距rmax等于9.510 1 m，再根据式(21)可得临界击距下的雷电流幅值Imax为4.101 1 kA。由电气几何模型的原理可知，暴露距离与避雷线、导线、大地三者的引雷曲线相关，假设幅值为I(I2≤I≤Imax)的雷电流在三者上产生的击距均为r，设A点为避雷线引雷段与导线引雷段的交线，B点为导线引雷段与大地引雷段的交线，设避雷线所在处为原点O，导线坐标为(a，b)，其值可通过导线、避雷线高度和保护角求得[21]。根据两圆相交可建立A点坐标方程为：

(27)

根据杆塔模型可得：

(28)

式中d为避雷线与导线间的距离为2.915 5 m，避雷线保护角α为22.166 3°。根据初步估计推算可知I在I2≤I≤Imax范围内的yA均大于0，且击距r小于hd，由此可绘制电气几何模型图如图5所示[22]。

图5 电气几何模型图Fig.5 Electrical geometry model

且暴露距离的计算式为：

Z=dsinα+r-xA

(29)

联立式(21)、式(23)、式(24)、式(28)、式(29)可求得绕击闪络率为0.26。

4.5 雷击跳闸率计算

安装压缩气流灭弧防雷间隙后，反击情况下的雷击跳闸率可由式(16)、式(19)求得，由于采取单根避雷线的方式，因此b可令为0，假设计算杆塔处在平原路段，击杆率g可取0.25，由此可得n1=0.001。绕击情况下的雷击跳闸率可由式(25)得n2=0.001，因此可根据式(26)得雷击跳闸率n为0.002次/(100 km·a)。此外，可求得未安装灭弧装置的雷击跳闸率为0.424 9 次/(100 km·a)，对比可知压缩气流灭弧防雷间隙大幅度降低了雷击跳闸率，并致使雷击跳闸率趋于零。

5 运行情况

压缩气流灭弧防雷间隙目前已在各地运行。广西某市某线路年雷暴日达到120以上，属于强雷区，线路经过区域雷电活动频繁，极易发生雷击事故，年平均雷击跳闸率到40次以上。2015年该线路进行改造安装，经过一年多的运行统计，该线路未发生雷击跳闸，其实际安装照片如图6所示。

图6 压缩气流防雷间隙在某市的安装运行图Fig.6 Installation and operation of CDPD in a city

6 结束语

本文利用实验与理论结合的方式搭建了配网线路在安装压缩气流灭弧防雷间隙后的雷击跳闸率数学计算模型，得到如下结论：

(1)根据气体放电理论得出了防雷间隙对绝缘子串的保护系数为99.993%，基于数理统计方法并依据工频电流灭弧实验数据得出了三段不同范围工频短路电流幅值的灭弧系数为0.993 6、0.999 2、0.999 9，从而改善了原有线路的建弧率；

(2)通过实际算例详细介绍了计算方法，并在该算例中得出在该35 kV配网线路上的雷击跳闸率为0.424 9 次/(100 km·a))，利用压缩气流灭弧防雷间隙安装改造后的跳闸率为0.002次/(100 km·a)，使得改造后下降幅度为99.5%；

(3)理论计算的结果与实际情况存在一定的差异，但根据现场具体运行情况验证了该灭弧设备能大幅度降低雷击跳闸率并趋于零。