调整接触网避雷线保护角降低雷电绕击概率的研究

刘继永，李威龙

（1.朔黄铁路发展有限责任公司，河北 肃宁 062350；2.北京交通大学电气工程学院，北京 100044；3.西南交通大学电气工程学院，四川 成都 611756）

常见的接触网雷害类型主要为直击雷和感应雷造成的过电压[1-5]。 无论何种雷击造成的过电压都会远远超过接触网设备的绝缘所能承受的数值，是造成接触网绝缘故障和跳闸事故的主要原因之一[6]，同时雷电放电所产生的大电流，有可能使被击物炸毁、燃烧、使导体熔断或通过电动力引起机械损坏，影响接触网的健康及使用寿命[7]。 为了保护接触网沿线设备[8-9]，提升接触网耐雷水平，一般会采用加装避雷线的方法对线路进行保护， 同等条件下，接触网线路架设避雷线后，雷电引起的感应过电压可降低20%左右[10]，对AF 线和T 线保护效果良好[11]。

在避雷线架设施工中核心的问题是确定避雷线的架设高度，避雷线架设高度的选择将直接影响避雷线保护范围的大小[12]，架设高度过低会导致保护范围不够， 架设高度过高又会使工程投资增加，因此确定合理的避雷线高度是避雷线架设过程中重要的环节。

林卫[13]利用滚球法计算了单线情况下的准朔铁路最小避雷线架设高度， 并比较了架设避雷线前后线路耐雷水平的变化；鲁相来等[14]针对武广高铁单线和复线两种情况分别进行了滚球法的高度计算，给出了参考的架设高度；赵紫辉等[15]基于电气几何模型分别推导出了单线和复线铁路的接触网避雷线架设高度的计算公式， 根据广深铁路接触网的结构特点及参数， 计算得出了其3 种形式线路的避雷线架设高度的建议值； 这些文献中计算校验后的避雷线高度能够确保将范围内的接触网设备保护在内， 但是在进行计算的过程中一般默认避雷线架设在支柱正上方对支柱两侧的设备进行保护，这样就忽略了避雷线保护角的问题，避雷线的保护角指的是避雷线与外侧导线的连接线和避雷线对地垂直线的夹角， 如果牵引供电采用AT 供电等方式，避雷线需要能同时保护支柱两侧的正馈线和承力索， 由于两侧设备到支柱的距离不同导致一侧保护角偏大， 保护角越大发生雷电绕击的概率也就越大， 一旦发生雷电绕击会对接触网设备造成巨大的危害。 针对这一点本文在滚球法计算公式中加入了避雷线安装位置到支柱距离参数， 该参数的加入可以改变避雷线的架设位置， 通过调整避雷线架设位置改变避雷线两侧保护角的大小，使两侧保护角大小相等，避免出现一侧保护角过大的情况。

1 未考虑保护角因素的避雷线架设一般高度校验计算

避雷针的高度计算方法一般有折线法和滚球法[16-17]，由于滚球法相对折线法更切合雷击的实际情况，并能科学地解释防止侧击雷问题，现在国际上大多采用滚球法作为避雷针高度计算方法，我国《建筑物防雷设计规范》[18]中也推荐使用滚球法，利用该方法可以计算出避雷线的架设高度，避免出现保护范围不足等情况，本文将采用滚球法进行避雷线高度计算。 滚球法是利用一个半径为的球体，沿着需要防直击雷的物体进行滚动，滚动过程中只触及避雷设备和地面而不触及被保护的物体，则球体所不能触碰的空间就是避雷设备防护的有效范围。

一般的高度校验计算中避雷线默认安装在支柱正上方，不考虑两侧保护角大小。在AT 供电等方式中支柱两侧都有接触网设备存在，即校验的标准是判断在该高度下避雷线能否同时保护支柱两侧的正馈线和承力索等设备，这里着重考虑单线区段利用一根避雷线进行保护的情况，保护范围的确定如图1 所示。

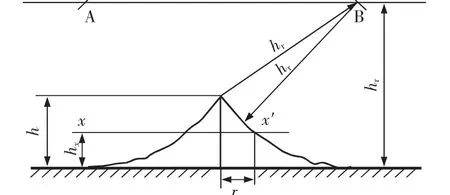
图1 滚球法确定避雷针保护范围Fig.1 Determination of lightning rod protection range by rolling ball method

图1 为单根避雷针的保护范围，避雷线可视作连续排列的避雷针，避雷线上一点即为一个避雷针针尖，要求架设的避雷线能同时保护承力索和正馈线, 参照单根避雷针的保护范围计算方法进行避雷线保护范围计算，根据滚球法的定义，要利用该方法进行计算首先要制造一个滚球圆令避雷针针尖位于圆上，且圆与地面相切，以A，B 两点为圆心作圆，两圆相切与地面，且避雷针针尖位于圆上，两圆圆弧与地面所围成的区域即为保护范围。 避雷针在hx高度的xx′平面的保护半径可以由式（1）计算

式中：rx为避雷针在hx高度的xx′平面上的保护半径，m；hr为滚球半径，按照《建筑物防雷设计规范》中的规定，接触网为一类建筑，hr取值30 m；hx为被保护物的高度，m；h 为避雷针针尖高度，m。

保护角α 的大小可以由式（2）计算

代入相关的避雷线高度等参数即可计算出相应的保护范围，由此可以判断被保护设备是否在保护范围内，从而确定避雷线高度选择是否合理。

2 考虑避雷线保护角因素的改进高度校验计算

利用滚球法对避雷线高度进行计算校验时，默认避雷线架设在支柱正上方，如式（1）中rx为避雷针在ηx高度的xx′平面上的保护半径， 实际上rx取值为被保护设备到支柱的距离，即以支柱作为保护半径的圆心，将避雷针置于此处。 避雷线默认架设于支柱正上方时， 如果要同时保护支柱两侧设备，例如正馈线和承力索， 由于两侧线路到支柱的距离不等，必然会导致一侧的保护角偏大，提高雷电绕击发生的概率。 因此对rx参数进行调整，将式（1）中避雷线架设位置由原来的支柱正上方改为使两侧保护角相等处。

1） 令新的避雷线架设位置到支柱即原避雷线架设位置距离为a，若rx1＜rx2，则有

式中：rx1为左侧设备到原避雷线垂直面的距离，即到支柱的距离，m；rx2为右侧设备到原避雷线垂直面的距离，m。

2） r′x1，r′x2为被保护设备到新的避雷线所在垂直面的距离，通过调整a 的大小使此时避雷线两侧保护角大小相等。 由几何关系可得

3）将式（3）、式（4）代入式（5）中可得a 与h 的关系如式（6）

式中：hx1为左侧被保护物的高度，m；hx2为右侧被保护物的高度，m。

4） 利用参数a 调整被保护设备到支柱的距离rx， 既可以得到避雷线两侧保护角大小相等条件下的高度计算式（7）

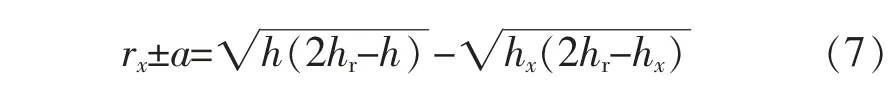
5） 对调整后的避雷线两侧保护角大小β 可由式（8）进行计算

当对利用该方法对避雷线保护角大小进行调整后，不会出现一侧保护角过大的情况，这对降低线路整体的雷电绕击概率是有益的。

3 改进前后雷电绕击概率试验比较

3.1 保护角大小对雷电绕击概率的影响

避雷线的保护不是绝对的，用避雷线来保护线路时，存在一定的雷电绕击概率，即雷电绕过避雷线击中被保护线路。 保护角和杆塔高度是影响绕击的重要参数，根据规程法的经验公式[19]，绕击率在平原和山区可分别由式（9）、式（10）计算

式中：P 为绕击概率；α 为避雷线对导线的保护角，（°）；hT为杆塔高度，m。

接触网支柱高度为9.2 m， 保护角在0°～40°范围内时，平原与山区地区的保护角与雷电绕击率关系如图2 所示。

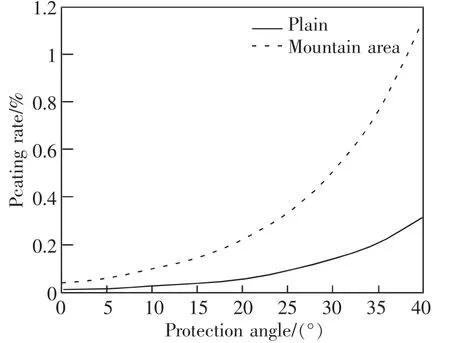
图2 平原与山区地区的保护角与雷电绕击率关系Fig.2 Relationship between protection angle and lightning shielding rate in plain and mountainous areas

由图2 可知雷电绕击率与保护角大小的关系，可见保护角越大发生雷电绕击的概率也越大，如果发生绕击，将会引起雷击事故，因此保护角不宜过大，一般在0°～40°范围内，平原地区雷电绕击率不超过0.4%，山区地区雷电绕击率不超过1.2%。

对于一根避雷线保护两侧设备的情况，两侧的保护角大小存在一侧偏大一侧偏小的情况，较大侧的保护角会使线路整体的雷电绕击概率偏大，不利于防雷保护，因此需要通过改变避雷线架设位置来调整避雷线两侧的保护角大小，使两侧保护角大小相近或相等，从而降低线路整体的雷电绕击概率。

3.2 改进前的雷电绕击概率计算

在平原与山区地区，保护角对雷电绕击概率的影响程度不同， 由于山区的雷击环境更加恶劣，这里以山区条件为例进行后续计算，式（10）可以分别计算出调整避雷线位置前后承力索侧和正馈线侧的雷电绕击率。

利用准朔铁路[13]实际接触网数据进行计算，支柱一侧正馈线高8.15 m，距离支柱1.35 m，支柱另一侧承力索高8.2 m，距离支柱3.1 m；接触网支柱高9.2 m，避雷线安装于距离接触网支柱顶端2.5 m处，即避雷线的安装高度为11.7 m，要求对该高度进行校验计算，判断能否同时保护支柱两侧的正馈线和承力索，完成校验后计算在该位置的避雷线保护角大小，并以此计算雷电绕击概率。

1） 避雷线保护角调整前的高度校验计算。

对正馈线进行保护范围校验：正馈线高hx=8.15 m，距离支柱1.35 m，由式（1）可得避雷线在该高度下保护范围rx=3.22 m，因此正馈线在保护范围内。

对承力索进行保护范围校验： 承力索高8.2 m,距离支柱3.1 m，由式（1）可得避雷线在该高度下的保护范围rx=3.16 m， 因此承力索也在保护范围内。由以上校验结果可知，避雷线安装高度11.7 m 能满足对下方接触网设备的保护要求。

以上均是关于混凝土结构抗碳化的研究成果，结果表明混凝土抗碳化受到多个因素影响，包括具体的涂层的材料、涂层的类别、涂刷遍数、涂层的封闭性等。

2） 由式（2）计算避雷线两侧保护角大小。正馈线测保护角为

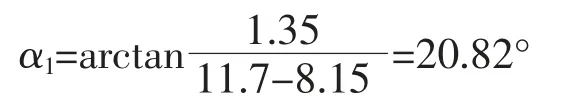
承力索测保护角为

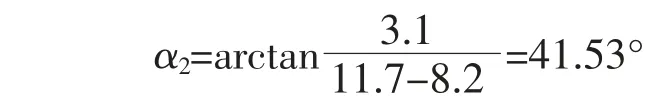
由以上计算发现， 承力索侧保护角明显偏大，一般要求接触网避雷线保护角大小在0 到40°之间，承力索侧保护角大小以及超出了这个值。

3） 由式（10）计算避雷线位置调整前的雷电绕击率。

正馈线侧的雷电绕击率为

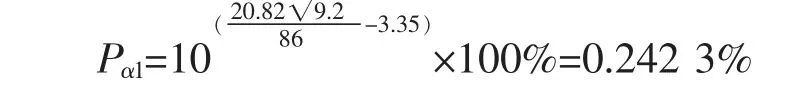
承力索侧的雷电绕击率为

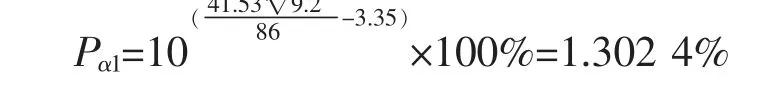
由承力索侧和正馈线侧分别的雷电绕击率可以求出整个避雷线保护范围内的雷电绕击的概率

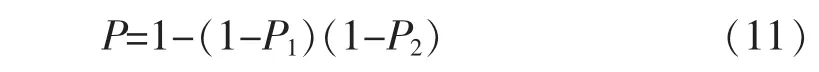
式（11）中P1，P2为避雷线两侧的雷电绕击概率。

由式（11）可得避雷线位置调整前整个线路的雷电绕击的概率为

3.3 改进后的雷电绕击概率计算

由前一节的方法可以计算出调整后的避雷线架设位置，在此基础上对调整后的避雷线高度进行校验，计算保护角大小和雷电绕击概率。

1） 避雷线保护角调整后的高度校验计算。

rx1，hx1为正馈线到支柱距离及正馈线距地面高度，rx2，hx2为承力索到支柱距离及承力索距地面高度，将参数代入式（6）可得a=0.891 m，即新的避雷线位置距离支柱0.891 m 位于承力索侧，r′x1=2.241 m，r′x2=2.09 m，由式（7）校验，确定避雷线调整后两侧设备仍在其保护范围内。

2） 由式（8）计算避雷线两侧保护角大小。调整后正馈线测保护角为

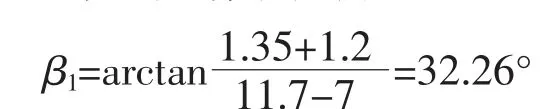
调整后承力索测保护角为

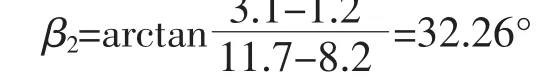
调整后两侧保护角大小相等，且原先偏大的承力索侧保护角由之前的41.53°减小到了32.26°，角度明显减小并且处于要求的0°～40°范围之内。

3） 由式（10）计算避雷线保护角大小调整后的雷电绕击率。

正馈线侧和承力索侧的雷电绕击率为

由式（11）可得避雷线位置调整后整个线路的雷电绕击的概率，即

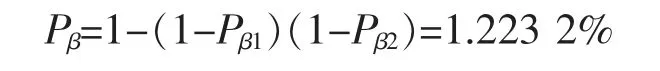
避雷线调整后，线路整体的雷电绕击概率降低了0.318 3%，为了确定该调整方法是否能较大程度的降低线路雷电绕击的概率，将它与理论计算的最小雷电绕击概率相比较。

为了计算最小雷电绕击概率，将式（11）P1，P2中保护角γ1，γ2用一个与避雷线调整距离a 有关的函数表示，即

上式中有rx1＜rx2，将式（12）、式（13）与式（10）代入式（11）中可得雷电绕击概率P 与避雷线调整距离a 的函数关系

式（14）中借助Matlab 软件绘制相同接触网设备参数下的最小雷电绕击概率与此时的避雷线调整距离大小关系曲线，如图3 所示。 由图3 可知，整体雷电绕击概率是先单调递减经过拐点后单调递增，是存在一个最小值的， 当避雷线调整距离a 取值0.9 m时，有最小雷电绕击概率1.223 1%，几乎与保护角相等情况的雷电绕击概率相等，此时的避雷线两侧保护角大小可由式（12），式（13）计算，正馈线侧保护角大小γ1=32.37°，承力索侧保护角大小γ2=32.15°。

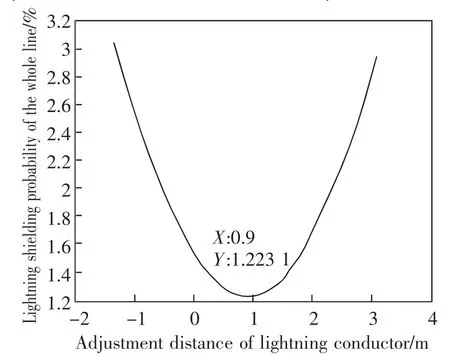
图3 避雷线调整距离与绕击概率的关系曲线Fig.3 Relation curve between adjustment distance of lightning conductor and winding probability

避雷线保护角调整前后雷电绕击概率如表1 所示。 由表1 可知，避雷线位置调整后的雷电绕击概率比避雷线直接架设于支柱正上方时的雷电绕击概率减少了0.318 3%，该方法将雷电绕击概率从之前很低的水平1.541 5%进一步减小到了1.223 2%，降低了20.65%，调整后的雷电绕击概率已经接近理论计算的最小值，可见令两侧保护角相等的调整方法有非常好的效果。

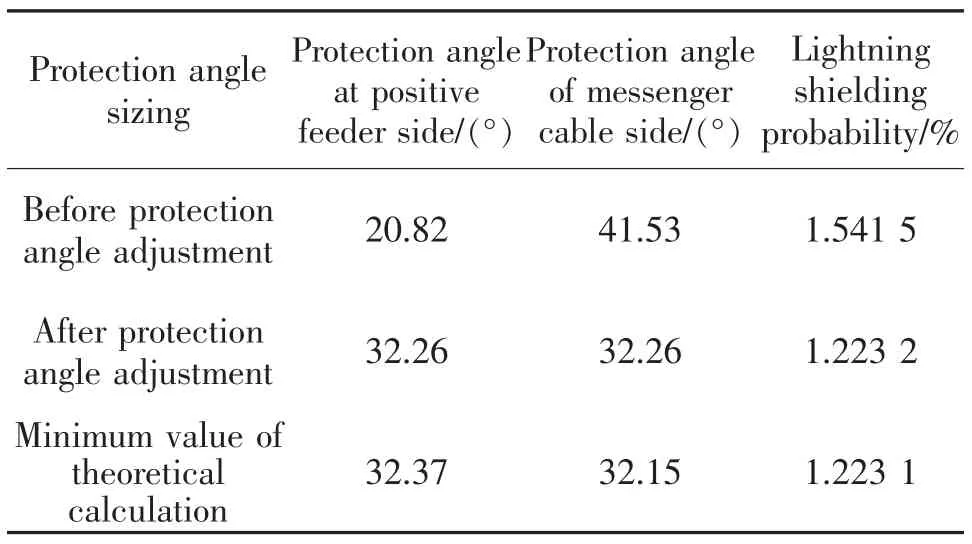
表1 避雷线保护角调整前后雷电绕击概率比较Tab.1 Comparison of lightning shielding probability before and after lightning protection angle adjustment

4 结论

考虑保护角大小对雷电绕击概率的影响，提出一种考虑保护角大小因素的避雷线高度计算方法，通过调整避雷线架设位置与支柱之间的距离改变避雷线两侧保护角的大小， 降低线路整体的雷电绕击概率。 通过实际接触网线路的参数计算与理论仿真结果比较对方法的有效性进行了研究，得到如下结论：

1） 该方法能有效降低线路整体的雷电绕击概率，参照准朔铁路接触网数据，利用该方法调整后线路雷电绕击概率降低了20.65%。

2） 理论仿真计算发现雷电绕击概率大小与避雷线调整距离近似一个开口向上的二次函数抛物线，即雷电绕击概率理论上存在一个最小值，雷电绕击概率随着偏大侧的保护角减小、偏小侧的保护角增大而向着雷电绕击概率理论最小值移动，由于不是标准抛物线，在两侧保护角大小接近的时候就已经取得最小值，而在两侧保护角相等的情况下非常接近最小值。

3） 仿真中雷电绕击概率随两侧保护角大小的变化情况说明考虑保护角因素的避雷线改进计算方法中令两侧保护角大小相等从而求取近似的雷电绕击概率最小值的思路是正确的。 利用避雷线改进计算方法得到的线路雷电绕击概率近似理论计算得出的最小值，说明了方法的有效性。

4） 在实际的工程中，通过调整避雷线架设位置即可改变保护角大小，从而可以有效的降低雷电绕击概率且不需要额外的成本。