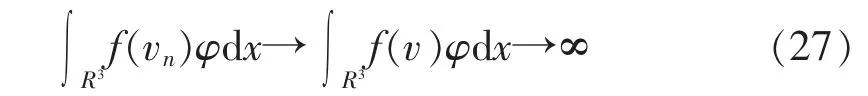双临界项的分数阶薛定谔-泊松方程组非平凡解

冯胜豪，王 莉，黄 玲

（华东交通大学理学院，江西 南昌 330013）

讨论了以下非线性分数阶薛定谔-泊松方程组的一个非平凡解的存在性。

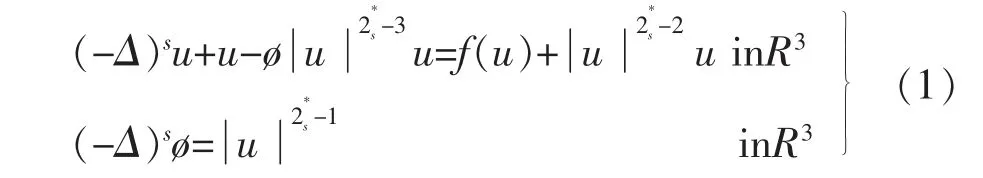
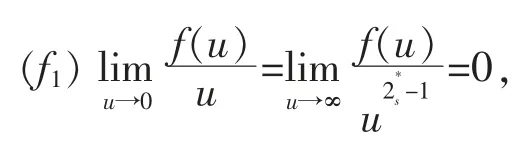
（f2） 存在u∈（2，2）使得

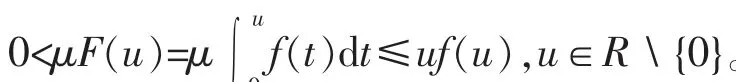
方程（1）更一般的形式为下列薛定谔-泊松方程组：

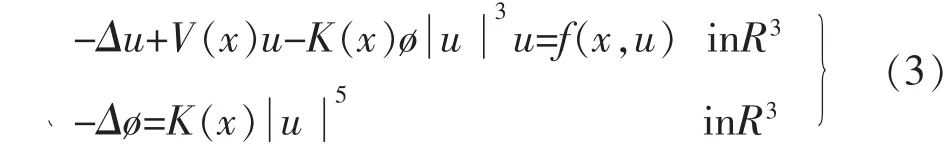
并利用山路引理和集中紧原理得到了方程（3）正解的存在性。 而涉及两个或多个非局部项的方程组问题研究较少。 Zhang 等[7]研究了分数阶非线性薛定谔-泊松方程组

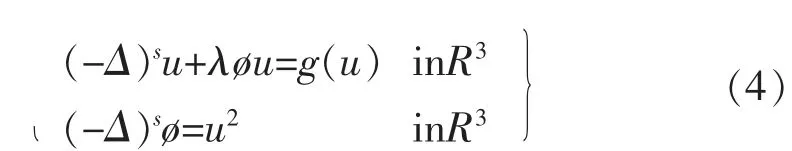
通过扰动法证明了方程（4）正解的存在性，并研究了含有参数λ 时方程解的渐近性。文献[8-9]有关于分数阶更多的薛定谔-泊松方程组的研究结果。

基于上述工作，本文通过变分法，也就是把方程的解转化为相应能量泛函临界点的问题， 即在寻找函数的极大和极小值。 主要目的是通过集中紧原理和山路定理证明具有双临界增长分数阶薛定谔-泊松方程（1）的非平凡解的存在性。

定理1.1假设（f1）和（f2）成立，则方程组（1）至少有一个非平凡解。

1 定义

在本节中我们将给出相关函数空间的定义和非局部项φ 的一些性质。 分数阶Sobolev 空间Hs（R3）描述如下

定义其内积和范数为

齐次分数阶Sobolev 空间

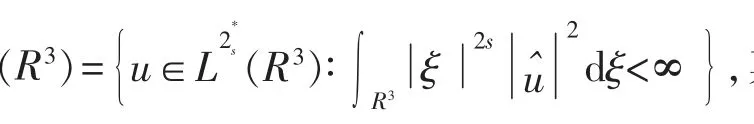
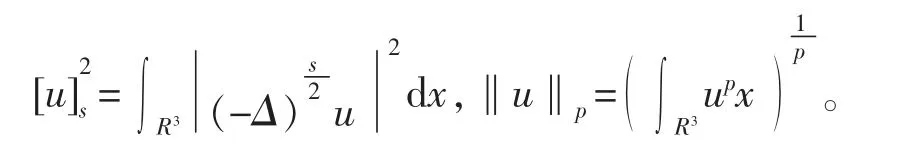
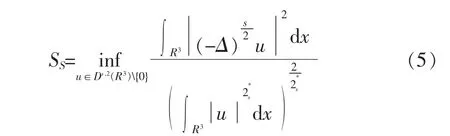
对于u∈Hs（R3），我们定义

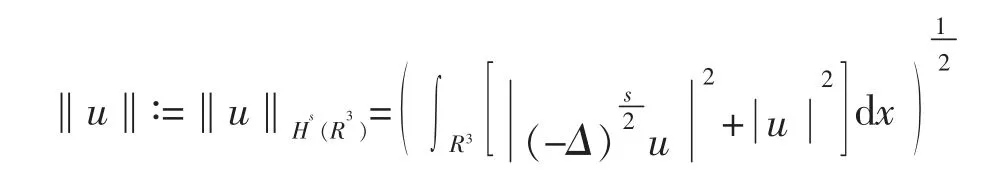
作为在Hs（R3）的范数，其内积为

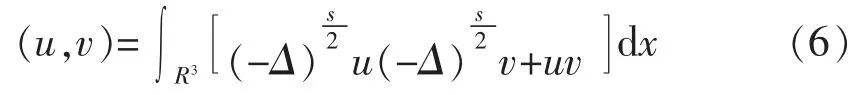
根据Lax-Milgram 定理，对∀u∈Hs（R3），存在唯一的φus∈Ds，2（R3）使得

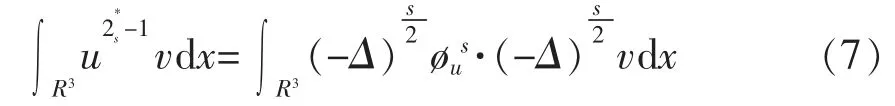
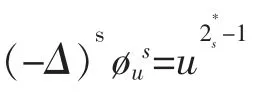
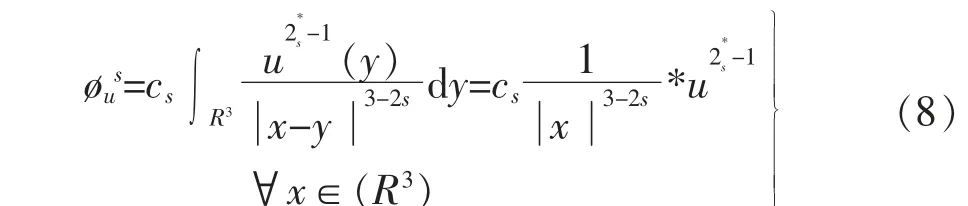
这叫做s-Riesz 势[12], 其中

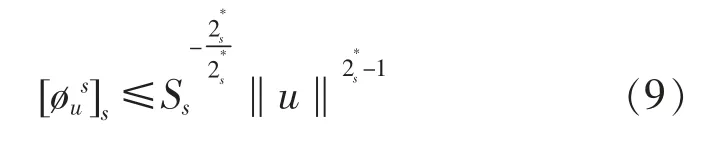
那么

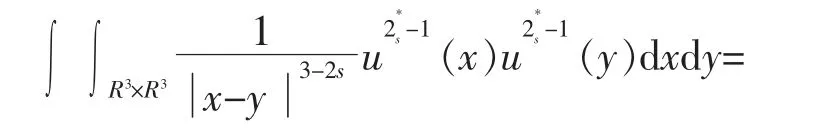
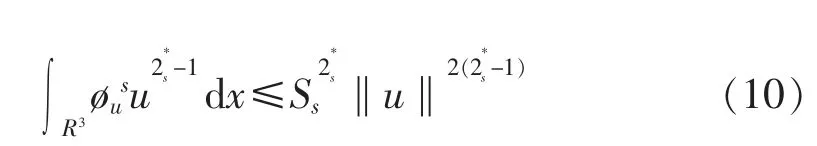
将φus替代φ 到方程（1），得到下面的分数阶薛定谔方程

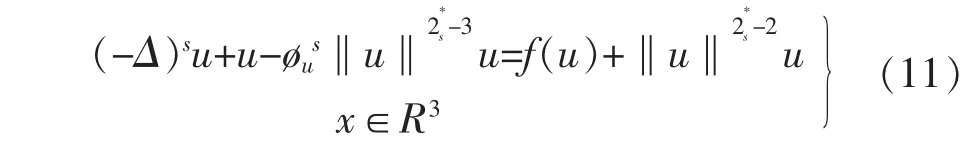
其能量泛函为

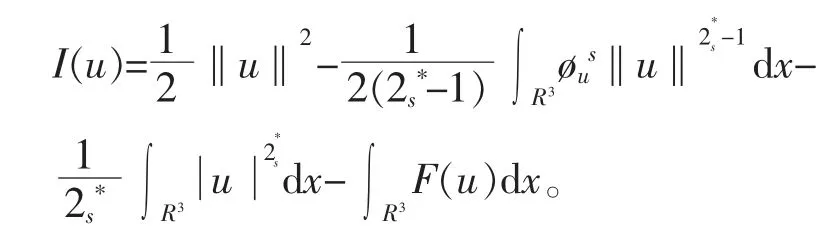
此外，由式（9）和式（10）知I（u）是C1泛函。对于任何v∈Hs（R3），可得

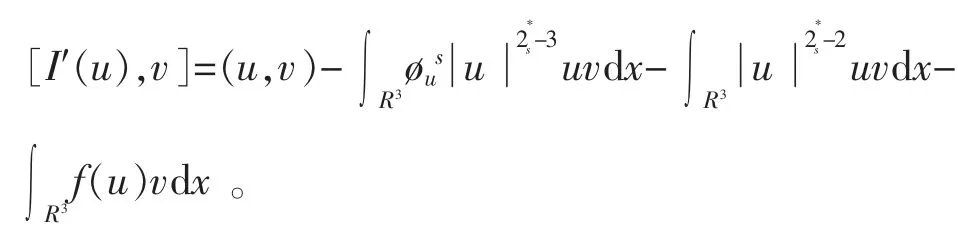
如果v∈Hs（R3）是一个临界点，则存在一对（u，φus）是方程（1）的解。

2 主要引理及其证明

引理2.1假设（f1）和（f2）成立，则存在ρ＞0，η＞0 使得当∀u∈Hs（R3）满足‖u‖=ρ 时有inf I（u）＞η＞0。

证明对任何ε＞0，根据（f1），（f2）和Sobolev 不等式知，存在Cε＞0 使得

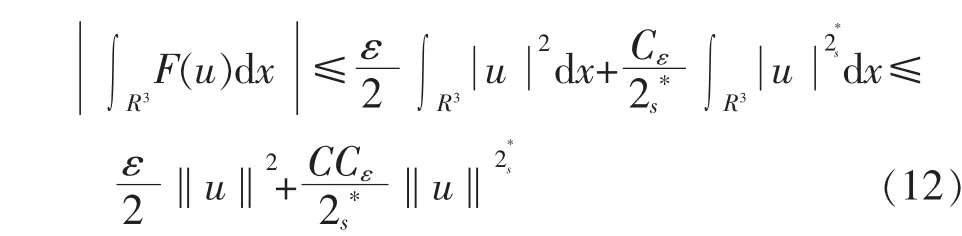
其中C 是一个正常数。 比较式（5），式（10），式（12），对于u∈∂Ωρ和C＞0，有

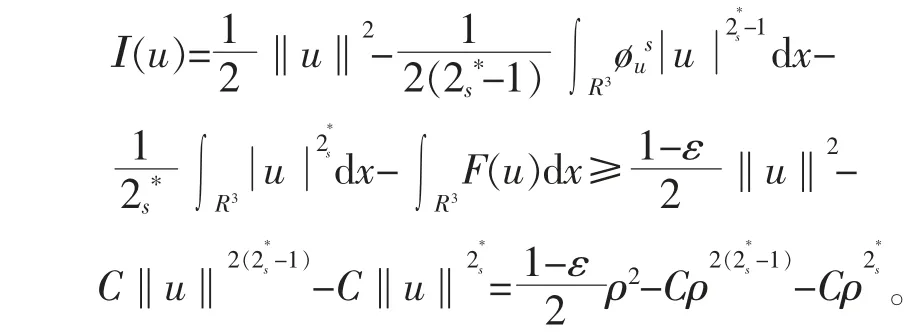
因为2＜min｛2s*，2（2s*－1）｝，选取ε∈（0，1），所以一定存在ρ＞0 足够小使得inf I（u）＝η＞0。

引理2.2假设（f1）和（f2）成立，则存在e∈Hs（R3）使得当‖e‖≥ρ 时有I（e）＜0，其中ρ 是引理2.1 给出的。

证明利用（f1）和（f2），可得存在M，L＞0，μ∈（2，2s*）使得

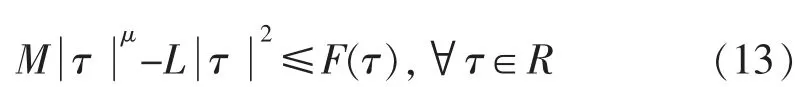
选择μ0∈C0∞（R3）｛0｝，通过引理2.1，当t→+∞，有

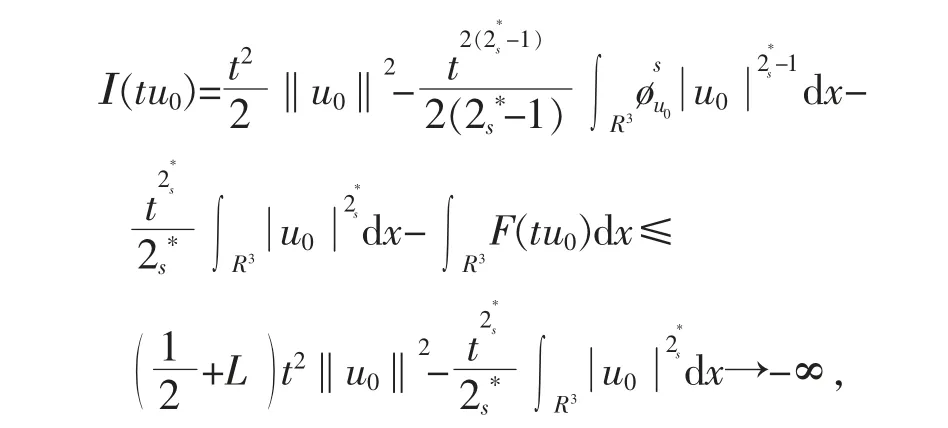
让T≥1 足够大使‖Tu0‖＞ρ，取e=Tu0，则有I（Tu0）＜0。

根据2.1，2.2 两个引理，可定义

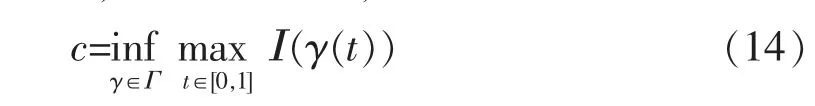
式中：Γ=｛γ∈C（［0，1］；Hs（R3））｜γ（0）＝0；I（γ（1））＜0｝。

引理2.3假设（f1）和（f2）成立，如果｛un｝⊂Hs（R3）是一个Cerami 序列，即

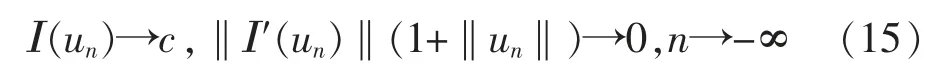
则｛un｝是有界的。

证明当n 足够大时，根据（f2）有

从而｛un｝在Hs（R3）是有界的。

引理2.4假设｛un｝⊂Hs（R3）且满足当n→∞时，有

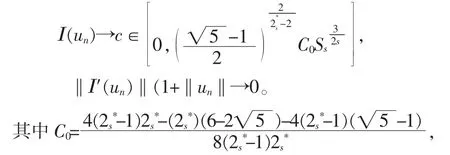
则存在｛yn｝⊂R3和R，σ＞0 使得

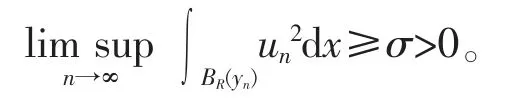
证明我们用反证法证明。 假设结论不成立，通过（f1）和（f2）可知

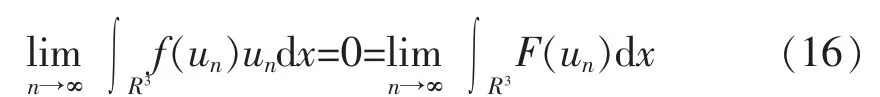
然后根据式（17）和［Ι′（un），un］＝On（1），当n→∞时，有

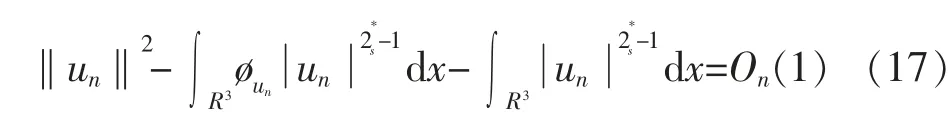
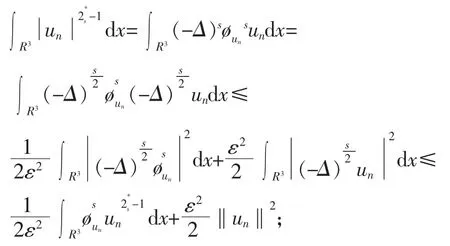
引理2.5设A，B，C＞0，定义h∶［0，∞）→R，其中

则有

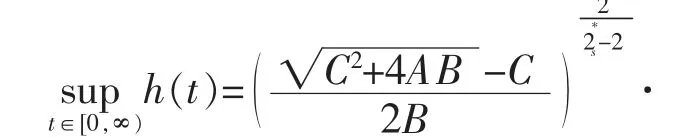
证明对于t≥0，有

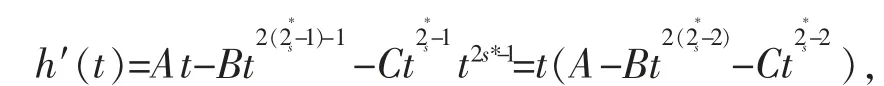
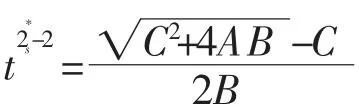
其中κ∈R｛0｝，τ＞0，x0∈R3。 根据文献[13－14]可以得到

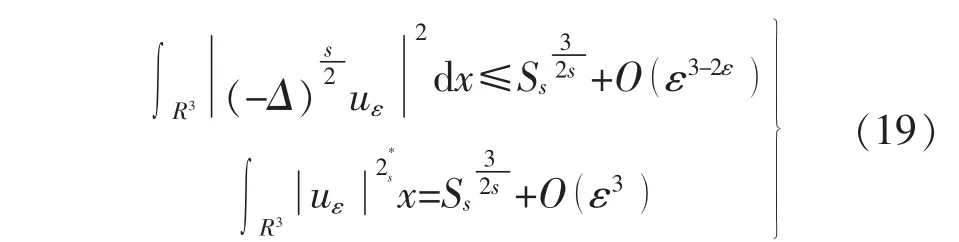
且

引理2.6令

则当ε→0+时，有

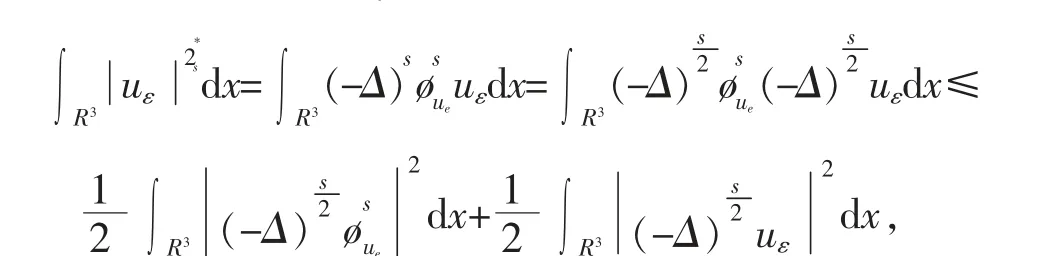
由式（19）可得，当ε＞0 足够小时，

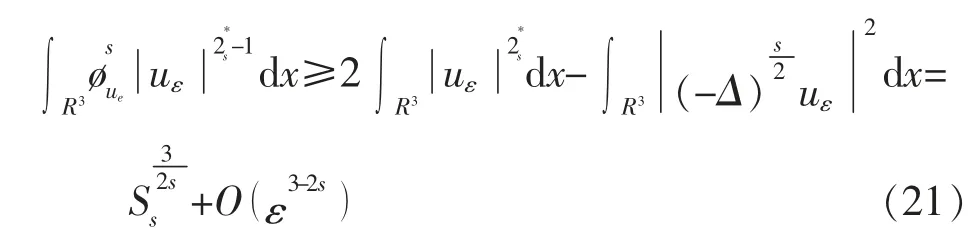
联合引理2.5 即得

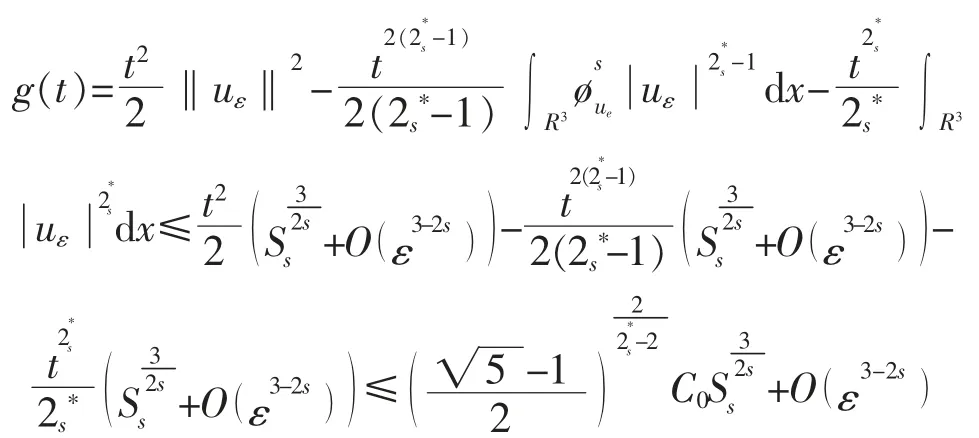
引理2.7式（14）所定义的c 满足

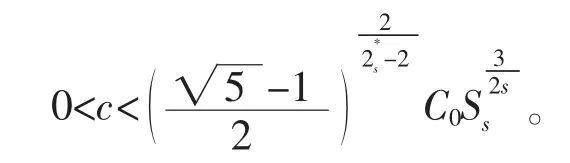
证明根据引理2.1 和引理2.2 知，存在tε＞0 使得

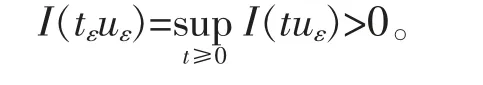
并且

由（f1）有

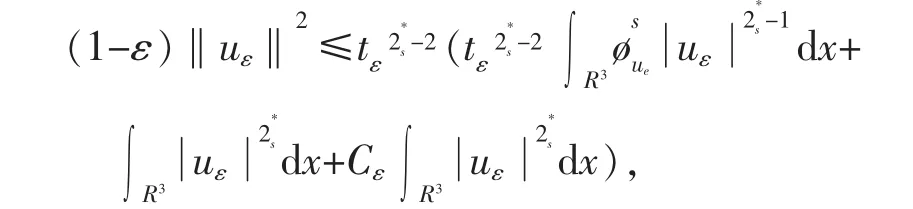
由I 的连续性， 存在ε1＞0，T1＞0 使得对任意的ε∈（0，ε1），有tε≥T1。

由（f2）有

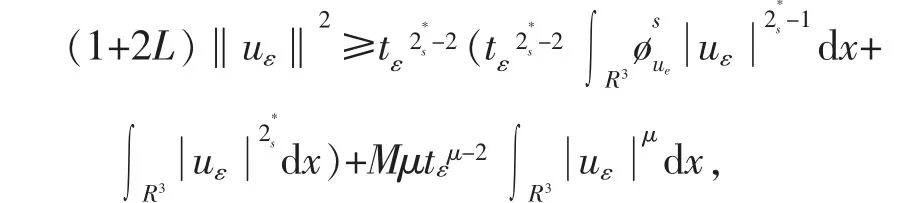
可知存在ε2＞0 和T2＞0 使得对任意的ε∈（0，ε2），有tε≤T2。

根据（f1）和（f2），存在M1，L1＞0 使得

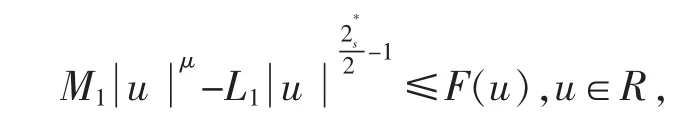
结合引理2.6，可以得到当ε＞0 足够小时，有

取ε＞0 足够小，由μ∈（2，2s*），有

3 主要结果的证明

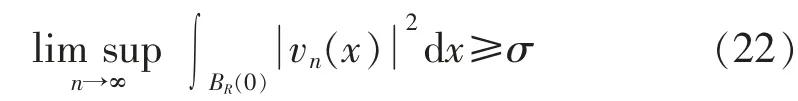
注意‖un‖=‖vn‖，则存在子序列，仍记为vn，vn∈Hs（R3）使得vn（x）→v，并且在R 内vn→v 几乎处处成立。 根据式（22）知v≠0。 选取φ∈C0∞（R3），可得

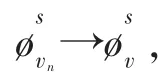
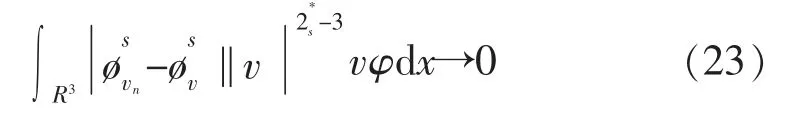
又因为

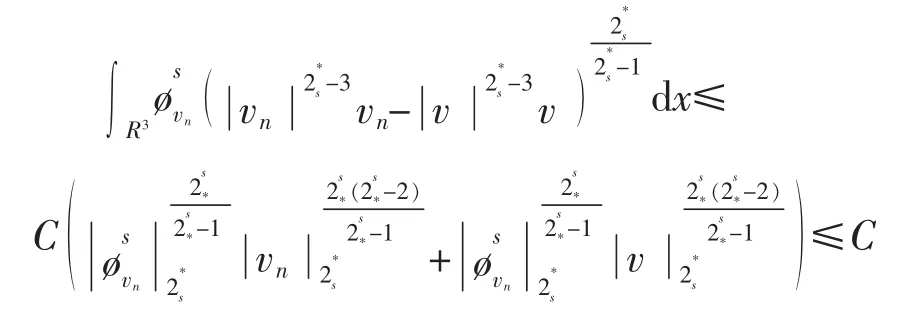
则当n→∞时，有

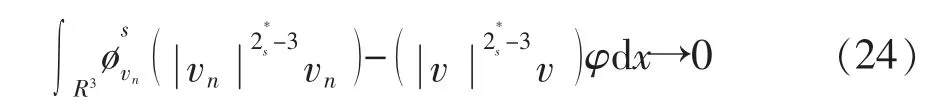
通过式（23）和式（24），发现当n→∞时，

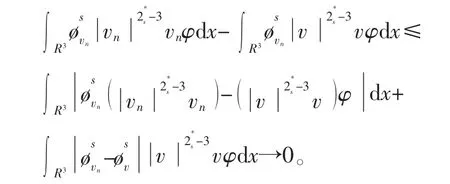
从而当n→∞时，有