车辆荷载作用下双工字钢-混凝土组合梁桥主梁动力分析

■李琼慧 尹栋佳

（湖北省交通规划设计院股份有限公司，武汉 430050）

随着交通量的不断增大， 城市桥梁得以快速发展。钢-混组合结构因能充分利用钢材和混凝土的优点，且便于施工，而被广泛应用。双工字钢-混组合梁桥作为钢-混组合梁桥的一种，在美国、日本、欧洲等国较为流行且学者们进行了大量深入研究，在我国则应用较晚，尚未形成完整的设计指导体系。荆国强等[1]对双工字钢-混组合梁桥的动力特性进行了研究分析；李彦伟[2]研究分析了钢梁的高度对双工字钢板组合梁的力学性能影响，给出了梁高的建议取值；江林松等[3]对双工字钢-混组合连续弯梁桥的有效宽度进行了研究分析，认为桥面板横断面正应力分布受弯扭耦合效应的影响较大，从而导致内、外侧主梁对应的桥面板正应力分布失去对称性。 综上可知，对于双工字钢-混组合梁桥的研究主要集中在截面形式、设计参数等方面，对双工字钢-混组合梁桥动力性能的研究较少[4-5]。 双工字钢-混组合梁桥由双主梁、剪力连接件、混凝土板组成。 主梁是桥梁的主要承重结构， 因此有必要研究分析双工字钢-混组合梁桥主梁的振动特性。本文依托ANSYS有限元软件，以三跨连续双工字钢-混组合梁桥为背景，建立了车-桥有限元模型，分析桥面不平顺、车速、车距等因素对主梁动力特性的影响。

1 车桥耦合分析模型

1.1 桥梁模型

我国某座三跨连续双工字钢-混凝土组合梁桥，跨径组合为30 m+30 m+30 m。 混凝土面板厚25 cm，选用C50 混凝土。 两纵梁梁高为150 cm，纵梁间距为750 cm，横隔梁标准间距为350 cm，钢梁采用Q345qD 工字钢。 钢梁和混凝土板通过剪力连接件连接。

利用ANSYS 软件建立三跨连续双工字钢-混组合梁桥整体模型（图1）。 混凝土桥面板采用实体单元建立，钢梁采用梁单元建立，剪力连接件采用弹簧单元建立。 桥梁动力平衡方程[6]如式（1）所示：

图1 双工字钢-混组合梁桥有限元模型

式中：Mb、Cb、Kb分别为桥梁的质量矩阵、 阻尼矩阵、刚度矩阵；δ、δ˙、δ¨分别为桥梁的位移向量、速度向量、加速度向量；Pb为桥梁受到的外力向量。

1.2 车辆模型

常用的车辆模型有单轮模型、1/4 模型、1/2 模型、三维空间模型。 三维空间模型由车体、悬架和车轮等组成。 假定三维空间模型的车身、悬架和车轮为刚体，3 种刚体之间通过弹簧阻尼器进行连接。车辆参数详见文献[7]，三维空间车辆模型如图2 所示。车辆振动方程如式（2）所示：

图2 车辆模型

式中：Mv、Cv、Kv分别为车辆的质量矩阵、 阻尼矩阵、刚度矩阵；Zv、Z˙v、Z¨v分别为车辆的位移向量、速度向量、加速度向量；Pv为车辆受到的外力向量。

1.3 车桥模型

假定车辆在行驶过程中不会发生跳车现象，并且考虑路面不平顺的影响，位移协调条件关系式如式（3）所示：

式中：Cw、Kw分别为轮组阻尼和刚度矩阵；Z˙r、Zr分别为轮组的相对位移向量和相对速度向量。

2 桥面不平顺生成

桥面不平顺服从高斯概率分布的随机过程，可采用桥面功率谱密度函数的傅里叶逆转换得到桥面不平整度[8]。

式中，f(nk)为功率谱密度函数；θk为0-2π 之间服从均匀分布的随机相位角；nk为空间频率。

图3 为桥面等级为A、B、C、D 级的样本曲线图。

图3 桥面不平顺样本曲线

3 主梁动力分析

3.1 桥面不平顺的影响

桥面不平顺对桥梁的动力响应有着重要影响，参数设置如下：车速为60 km/h，桥面等级为A、B、C、D 级，加载车道为2#车道。 中跨跨中的钢梁竖向位移时程曲线如图4 所示。

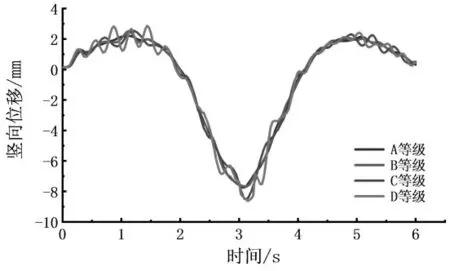
图4 钢梁竖向位移时程曲线

由图4 可知，随着桥面不平顺的退化，钢梁竖向位移时程曲线波动加剧。当桥面等级从A 等级退化到D 等级时，工字钢梁的竖向位移绝对最大值由7.37 mm 增大到8.43 mm，位移值增加了14.4%。

3.2 行车间距的影响

车间距是影响车桥耦合振动的另一个因素。 对车间距进行研究，采用2 辆加载车，以90 km/h 的车速通过B 等级的路面， 车间距分别为5、10、20 m。中跨跨中钢梁竖向位移时程曲线如图5 所示。

图5 钢梁竖向位移时程曲线

根据图5 可知， 车辆从桥头行驶到中跨跨中时，桥梁产生的振动大于车辆从中跨跨中行驶到桥尾时桥梁产生的振动。 当车辆间距由5 m 增加到20 m 时，位移时程曲线发生轻微波动，说明车距的不同虽会影响桥梁的振动，但影响程度较小。

3.3 车速的影响

为研究车辆行驶速度对钢-混组合桥梁动力响应的影响，设置如下参数：车重为35 t，车辆数为2 辆，车间距为5 m，路面不平顺等级为B 级，车辆行驶速度分别为30、60、90 km/h。 分析3 种车速下钢梁的动力响应，工字钢的中跨跨中竖向位移时程曲线如图6 所示。

图6 钢梁竖向位移时程曲线

根据图6 可知，当车速由30 km/h 增加到90 km/h 时，钢梁中跨跨中的竖向位移绝对最大值从7.79 mm 增加到10.35 mm，位移值增加了32.8%。

3.4 车辆数的影响

单幅双工字钢-混组合梁桥由单向两车道组成，单车以60 km/h 的速度分别通过路面等级为B的1# 车道、2# 车道，及双车同时以60 km/h 的速度通过路面等级为B 的2 个车道。车辆加载方式如图7所示，中跨跨中工字钢竖向位移时程曲线如图8所示。

图7 车辆加载数

图8 钢梁竖向位移时程曲线

根据图8 可知，车辆在1# 车道、2# 车道、双车道加载时，钢梁竖向位移绝对最大值分别为2.61、7.5、10.67 mm。

3.5 车辆按最不利加载与标准车道加载影响分析

考虑到桥梁横向的不确定性，选取车辆按最不利工况行驶及按标准车道行驶的2 种加载进行研究分析。工况一（偏载），车辆在距路边缘0.5 m 处行驶时为最不利位置行驶；工况二（中载），车辆按标准车道沿着道路中心线行驶。 车辆以60 km/h 速度通过路面不平顺等级为B 级的桥面。车辆加载工况如图9 所示，中跨跨中处钢梁竖向位移时程曲线如图10 所示。

图9 车辆加载工况

图10 钢梁竖向位移时程曲线

由图10 可知，偏载和中载作用下，工字钢的竖向位移差值为2.59 mm， 中载下钢梁跨中竖向位移大于偏载下钢梁跨中竖向位移值。 车辆在不同位置加载对结构影响不同，因此为准确研究结构的性能需要基于车辆实际的加载方式。

3.6 混凝土强度的影响

为研究混凝土强度对主梁动力特性的影响，设置如下参数：B 等级的路面，80 km/h 的速度， 混凝土强度为C40、C50、C60。中跨跨中钢梁竖向位移时程曲线如图11 所示。

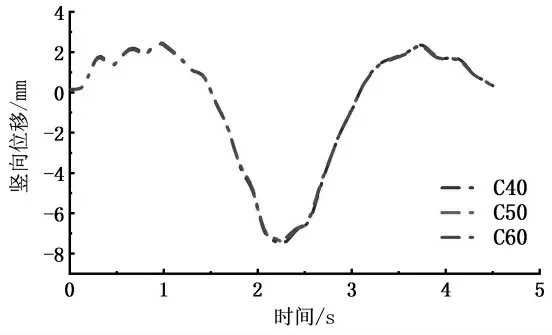
图11 钢梁竖向位移时程曲线

由图11 可知， 混凝土强度对主梁竖向位移的影响很小。

4 结论

（1）随着桥面的退化，主梁位移时程曲线波动加剧。 当桥面不平顺等级从A 级退化到D 级，钢梁的竖向位移绝对最大值由7.37 mm 增大到8.43 mm，位移值增加了14.4%。 因此，要及时加强路面的养护工作，不仅可以提高行车舒适性，而且可以有效减轻结构的振动。 （2）随着车速的增大，钢梁中跨跨中的竖向位移绝对最大值从7.79 mm 增加到10.35 mm，增加了32.8%。 因此，有必要限值行车速度，不仅能保证行车安全，而且可以有效缓解主梁的振动。 （3）车辆分布不同对结构影响存在差异，为准确研究结构的性能需要基于车辆实际的加载方式。 （4）混凝土强度的改变对主梁振动影响很小。