基于模糊蚁群算法的城轨交通网络节点分配优化策略

邵东波，杨春林，钱 平，王 芳

(1．中南大学 自动化学院，湖南 长沙410083；2．成都地铁运营有限公司 维保分公司，四川 成都610017)

0 引言

伴随着我国经济水平的发展，城轨交通规模也呈现指数型增长．北上广深、南京、西安、成都等全国一线城市的城轨交通网络覆盖范围越来越广，城轨交通网络布局和优化成为一个新的研究方向[1]．

城轨交通网络是一个复杂的网络拓扑结构，文献[2]从网络拓扑建模出发，研究动态网络路由调度分配策略．文献[3-4]从网络中心性角度出发，评估网络拓扑中节点的重要性，识别网络中的核心节点，从而对节点进行排序实现最优分配．此外，文献[5-6]分别利用K-means聚类和模拟退火方法，在复杂网络环境下确定核心节点，评估网络的鲁棒性．为了最大化网络效率和容量，文献[7-10]分别利用多目标调度与K-最短路径方法对网络节点的属性进行分配．此类算法针对节点自身属性进行分配，虽然可以取得局部最优解，但是无法最优化网络配置．

针对复杂网络优化问题，文献[11]提出利用蚁群算法实现电网的节点优化．而文献[12-13]将蚁群算法应用于列车调度和公交网络模型优化问题．文献[14]进一步将蚁群算法与K-最短路径方法相结合研究突发状况下的路径选择问题．文献[15]提出利用BFO细菌觅食优化算法进行交通调度优化．虽然上述方法均能在一定程度上实现多目标动态优化问题，但并未考虑节点自身属性，因此可能存在局部节点辐射能力不足的问题．

针对现有算法无法兼顾节点属性分配和全局网络最优化匹配的问题，为了实现网络多节点优化分配，本文提出利用模糊蚁群算法的城轨交通网络节点分配策略．首先构建目标函数，将多目标优化问题转化为节点模糊判决与蚁群优化两个问题．并通过模糊映射对节点属性进行模糊判决，最后利用蚁群算法搜索目标函数最优解．仿真结果表明，本文所提算法相对于现有算法具有更优的节点分配效果，且能够快速收敛到最优解．

1 系统模型

为了满足城市化需求，城轨交通发展成为必然趋势．据不完全统计，中国城轨交通已批复总长度超过7 000 km．其中，北上广深和成都等城市建设条数均超过十条，并形成了复杂的城轨交通网络．为了有效提高交通网络的效率，需要对城轨交通进行网络节点优化分配．

如图1所示，城轨交通网络中的节点主要分为3类，即核心节点、中间节点和边缘节点．核心节点是不同线路间的换乘节点，其选址以及换乘线路的数量决定整个交通网络的效率．中间节点是在核心节点之间的连接节点，其覆盖周围流量，且实现双向联通．边缘节点是每条线路的末端节点，实现单向联通．

在3类节点中，边缘节点是根据城市发展规划确定，一般处于城市边缘地区．而提高城轨交通网络效率主要是确定核心节点的数量及规模结构．

如图2所示，城轨交通网络拓扑结构主要分为3类，分别为方格式、放射式和环状式．拓扑结构中的交汇点为不同线路之间的换乘节点．在城轨交通网络中，规划和分配网络中心节点，能够有效提高交通网络效率．

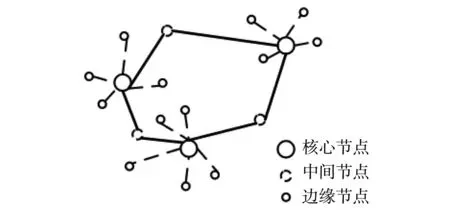
图1 城轨交通网络示意图

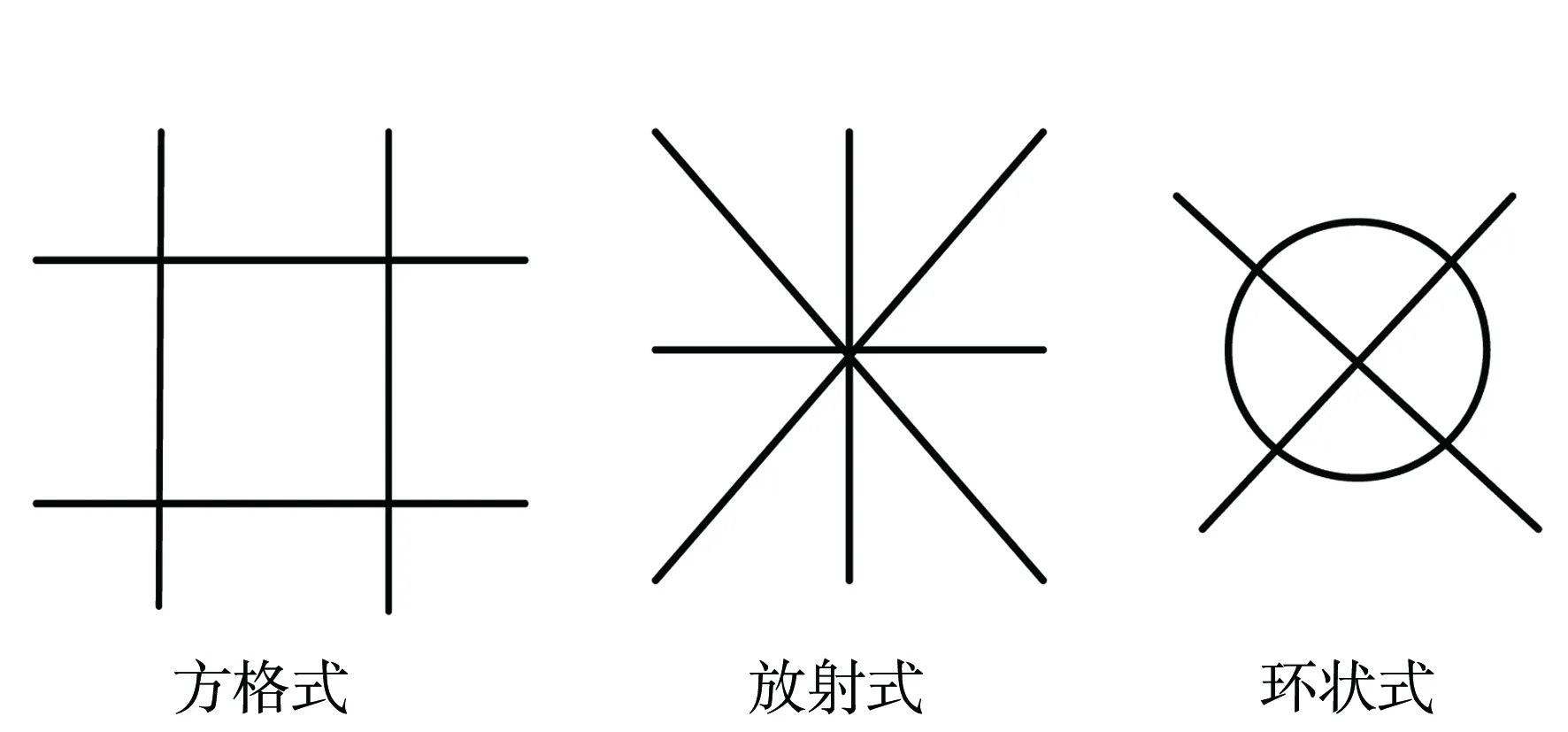
图2 城规交通网络拓扑结构

2 优化指标

城轨交通网络规划需要综合考虑各个因素．从图3可以看出，城轨交通网络规划是一个混合网络规划问题．其既要考虑静态网络中的网络拓扑结构和网络规模，同时又要针对动态网络中的客流特征与分布进行规划，从而最终确定整个交通网络的承载能力和网络效率[16-17]．

城轨交通网络要实现优化分配，并提高承载能力和网络效率，则需要分为静态网络评估与动态网络评估两部分进行评估．动态网络评估是根据人流量和周围产业分布情况等综合因素来评估节点设置的需求．而静态网络评估指标主要分为3大类，包含网络节点局部属性，节点的全局属性以及节点的连通属性，如图4所示．

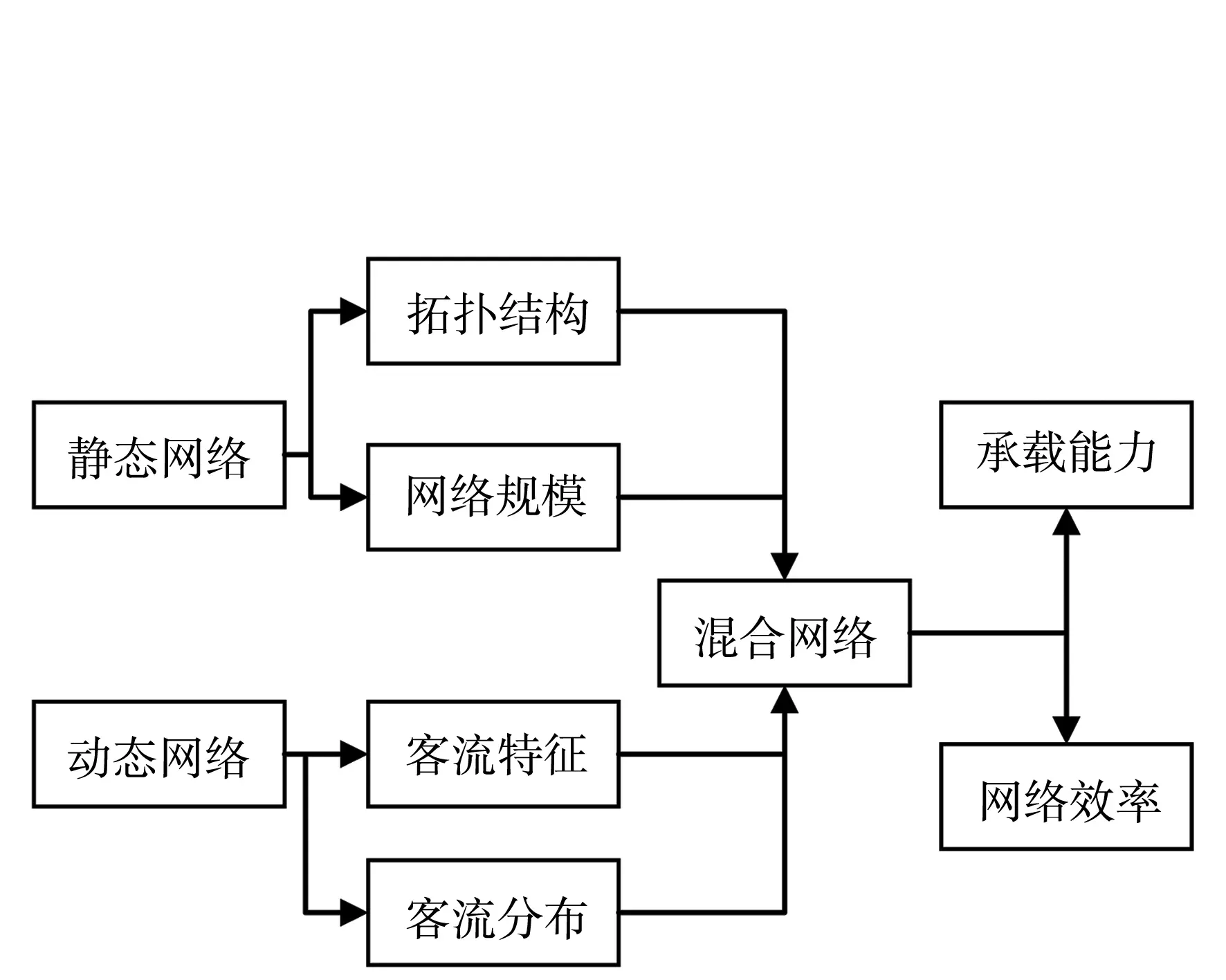
图3 城轨交通规划策略

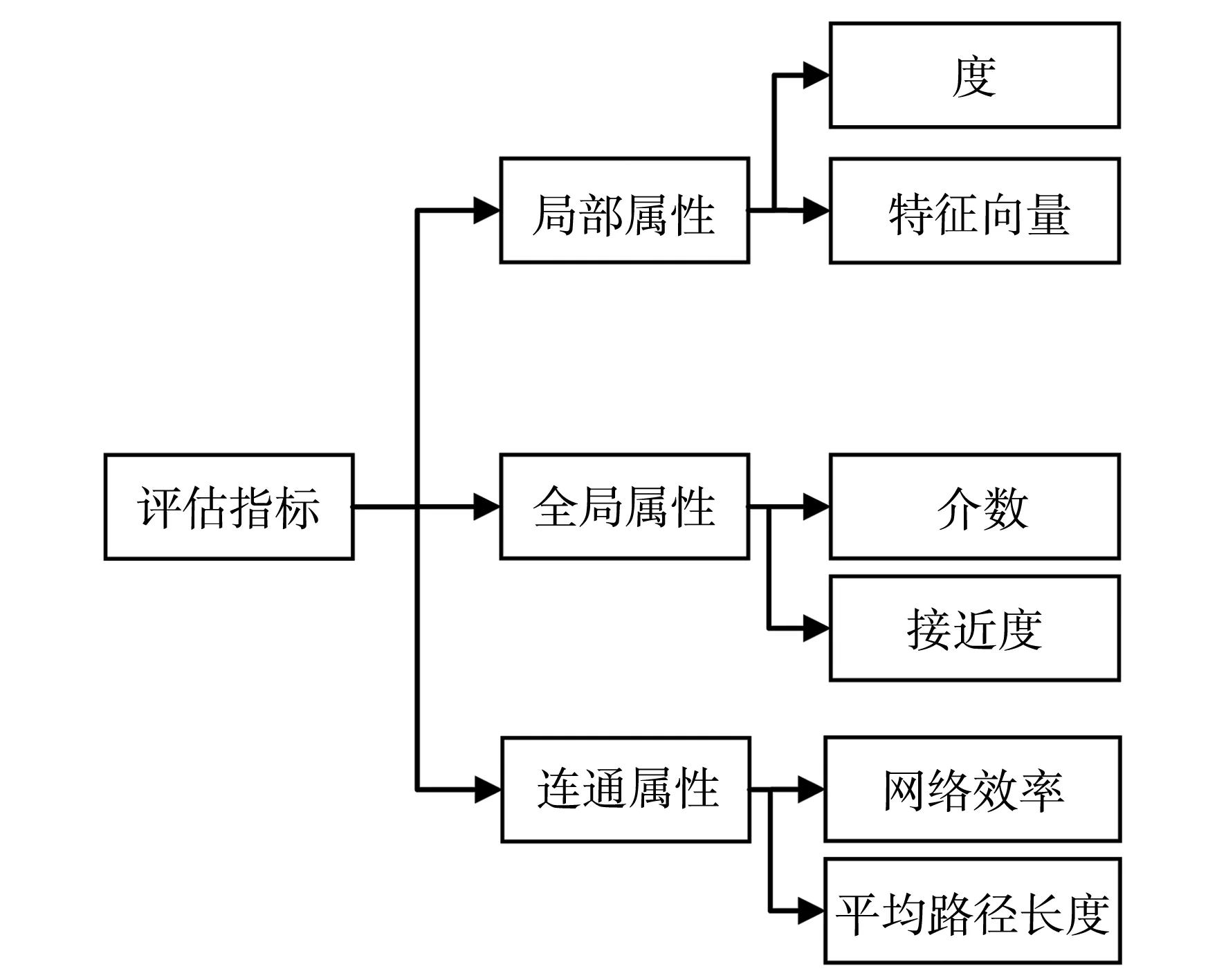
图4 静态网络评估指标

度表示某一节点的邻边数，即与该节点连通的节点数量．节点的度表示为：

(1)

式中，ki表示第i个节点的度，aij表示交通网络邻接矩阵中第i行j列的参数，N表示节点总数．

特征向量是对度的补充，即虽然某些节点的度不高，但其连接节点可能是一个具有高度值的核心节点．此时，该节点也相对较为重要，特征向量定义为：

(2)

式中，λ表示邻接矩阵的特征值，ej为邻接矩阵特征向量的第j列．

介数定义为经过该节点的最短路径数量与网络中最短路径总数之比，能够表征节点在网络中的重要程度：

(3)

式中，σi表示通过节点i的最短路径数，σij表示节点i和j之间的最短路径数．

接近度定义为节点到其他节点最短距离之和的倒数，表征到其他节点的难易程度：

(4)

式中，dij表示节点i和j之间的最短距离．

节点的局部属性和全局属性是评估节点设置合理性的指标．对网络进行评估需要使用连通属性[18]，即评估网络效率与平均路径长度．网络效率定义为：

(5)

平均路径长度定义为：

(6)

动态评估主要定义节点辐射容量参数，即某一节点对周边的辐射能力：

(7)

式中，μ表示调节参数，pi和P分别表示第i个区域及核心区域的人口．wi和W分别表示第i个区域与核心区域的就业岗位．di表示第i个区域到核心区域的距离．

3 算法架构

为了实现交通网络节点优化分配，需要确定最优化目标．根据第2节分析，交通网络主要包含静态拓扑结构和动态辐射容量两个参数，并以此确定节点的选定与分配．

根据定义，交通网络最优化时，网络效率和辐射容量均达到最大值．因此定义函数：

G=ηE+(1-η)∑Fi

(8)

式中，η表示模糊系数．则目标函数可以表示为：

max(ηE+(1-η)∑Fi)

s．t． 0≤η≤1

(9)

目标函数是一个多目标优化问题，无线性解[19]．因此本文提出基于模糊蚁群算法的交通网络节点优化分配方法，其流程框图如图5所示．

算法主要分为参数模糊处理与蚁群搜索两部分．其中参数模糊处理主要是针对各节点的参数进行处理，并根据模糊隶属度函数计算生成模糊隶属度集合，然后再进行计算和综合判决．节点参数模糊化处理流程，如图6所示．

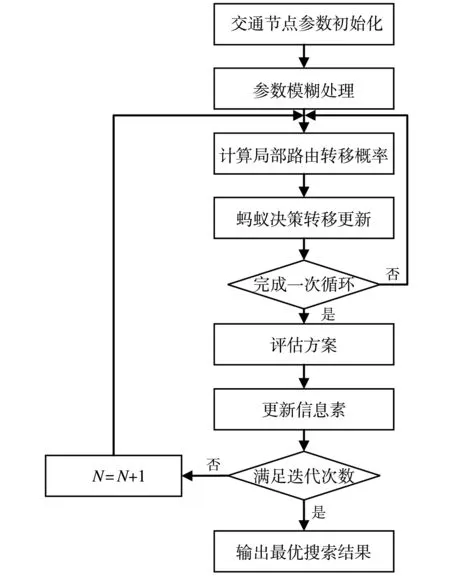
图5 模糊蚁群交通节点优化分配算法框图

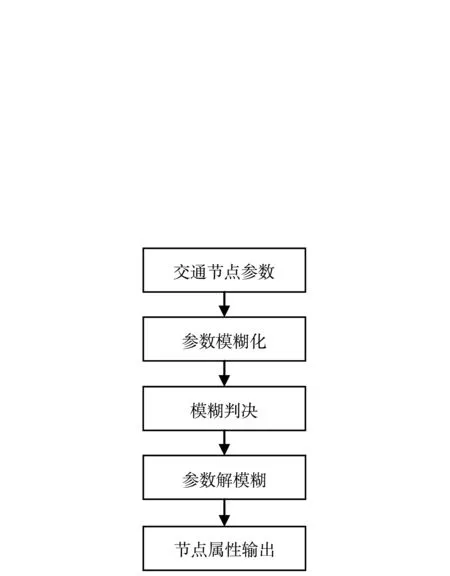
图6 节点参数模糊处理流程框图

首先定义两个集合，评判因素集Q={q1，q2，…，qm}与参数状态集合V={v1，v2，…，vn}．其中，评判因素主要包括节点区域人流量和工作岗位、附近核心区域的人流量和工作岗位；状态集合主要包括，交通节点v1和非交通节点v2两种．

判决因素集和节点之间的模糊映射可以表示为：

f：Q→Φ(V)

(10)

式中，Φ(V)是集合V的非空模糊集合．常用的模糊映射函数包括三角函数，梯形函数和高斯函数等[20]．考虑到交通网络节点配置的多维评价指标，本文使用灰色关联模糊函数来计算模糊隶属度集合R．

(11)

其中，rm1=1-rm2，rm1和rm2的取值根据灰色关联理论计算得出[21]．

定义各评判因素的权重集合A，因此模糊判决运算可以表示为：

W=A×R=[wy，wn]

(12)

根据模糊判决矩阵W的元素wy和wn的大小关系来确定每一个区域是否需要设立交通节点．在确定节点配置之后就可以对整个网络进行最优化匹配．

假设蚂蚁数量为N，x→y表示蚂蚁可以由x转移到y，则第k只蚂蚁随机转移概率定义为：

(13)

式中，γxy表示信息能见度，即x和y之间的信息能见度，其是距离的倒数．τxy表示每条路径上的信息素，信息素更新公式为：

(14)

根据转移概率转移蚂蚁，并在所有迭代完成后对方案的目标函数进行评估，得到网络节点的最优配置方式以及换乘最优路径．

4 仿真验证及数据分析

为了评估本文所提出算法的有效性．根据2020年的成都轨道交通数据来配置网络节点进行实验，其中节点数为308个，线路共计12条．区域人口数据使用2020年的人口普查结果．蚂蚁个数设置为节点数的1．5倍，对比分析了现有算法与所提算法优化的节点覆盖能力和网络效率．同时，通过分析本文所提算法在不同迭代次数下的网络效率与目标函数值，来验证所提算法运行效率．

表1是本文算法与现有算法网络节点分配之后的性能对比．通过对比可以发现：K-means聚类算法在节点平均度和平均介数的性能较好，辐射能力也较高，但是网络效率较低，说明K-means聚类算法更适合局部优化；BFO算法和蚁群算法性能基本相当，整体优于模拟退火算法；本文所提算法在辐射能力和网络效率均优于对比算法，说明其在节点局部属性和整体网络规划上的分配均更优．

从表2可以看出，随着迭代次数增加，网络效率和目标函数均得到提高，且提高幅度逐渐变小直至不变．说明算法随着迭代性能会逐渐提高但存在上限，其在迭代40次之后，算法性能逐渐收敛，即达到最优解．此外，算法达到最优解的迭代次数与网络规模大小有关．

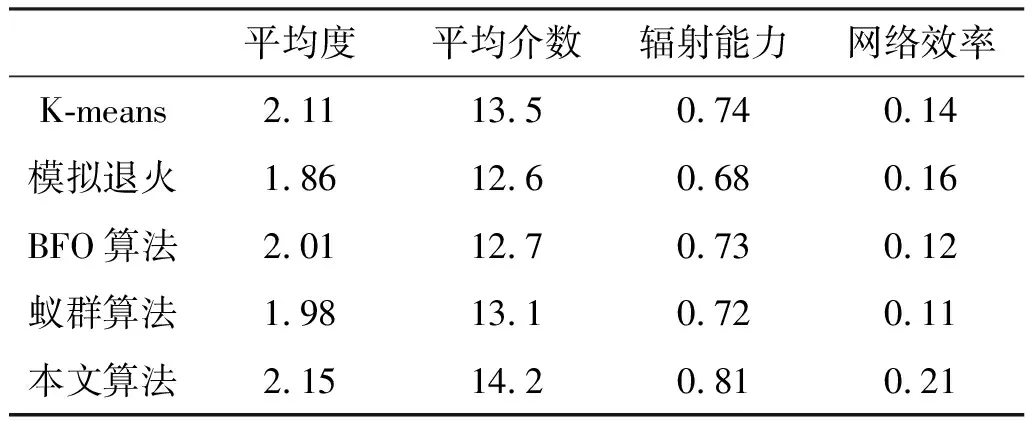
表1 不同算法交通网络节点分配指标对比

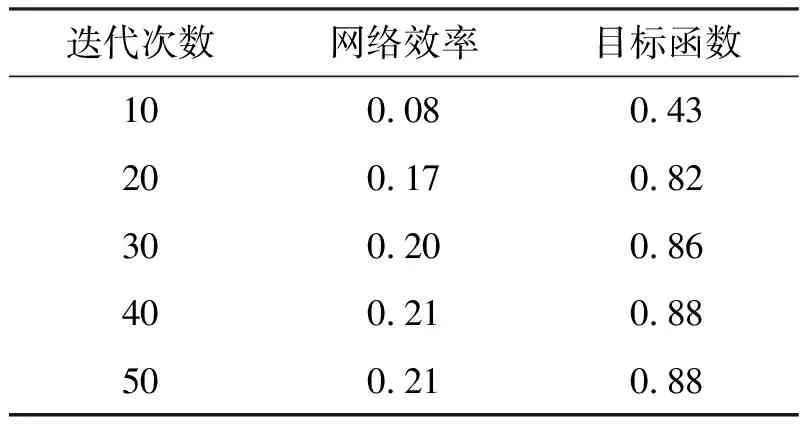
表2 不同迭代次数下模糊蚁群算法性能对比

5 结语

针对现代化城轨交通网络优化配置的需求，本文提出了基于模糊蚁群算法的交通网络节点分配优化策略．不同于现有算法，本文综合考虑了节点局部辐射能力和整体网络效率，并将目标优化问题分解为节点覆盖容量和网络效率局部最优解问题．再分别利用模糊理论对节点覆盖能力进行判决排序．在此基础上，利用蚁群算法进行最优解搜索，即可实现最优解快速迭代，因此具有一定的工程意义．后续工作可结合更多元的模糊判决因素与复杂的拓扑网络进行研究．