六轴机器人奇异点规避算法研究

肖永强 詹庆荣 方明

（埃夫特智能装备股份有限公司，安徽芜湖，241000）

0 引言

随着工业应用对作业精度的不断提高，其对机器人运动性能的要求也越来越严格，因此在机器人学中，机器人轨迹规划研究占据极为重要的地位[1]。在对串联机器人进行操作与控制时，机器人尚存在一定问题，如奇异点问题。当机器人运动到奇异点附近时，由于速度雅可比矩阵不可解性，导致加速度突变，发生机器人关节速度不可控现象，进而对机械本体造成较大的冲击、振动，损伤机械本体[2-3]。为了规避奇异点问题，使机器人运动更平稳，国内外诸多学者对此做了大量研究。

其中，哈尔滨工业大学等高校通过牺牲部分运动方向上的精度，对奇异点进行阻尼修正[4-5]。Wampler 及Kricanski 博士提出“阻尼最小方差”方法，通过对运动学逆解中雅可比矩阵进行修正，达到奇异点规避[6]。其关键在于，选择合理的阻尼因子，阻尼因子越大，运动性能越好，但运动精度会随之下降。为了解决此问题，徐文福[7]等人提出一种新的奇异点规避算法。其提出的“奇异分离与阻尼倒数”方法，运算量小、实时性好，可获得奇异区内的连续平滑速度，但牺牲了一部分末端奇异方向的精度。陈皓[8]等人根据示教运动特征,设计了一类奇异位形预测算法，预测并改善了示教调试过程中奇异性、不可达等问题，但没有解决奇异位形问题。于权伟[9]等人提出一种“分离-重构”技术求6R 机器人逆解的新方法，此方法求得的机器人逆解可规避奇异点影响，但该方法在进行结构分离时需要满足一定条件，具有局限性。董伯麟[10]等人提出一种连续阻尼自适应调节方法，然而在奇异位形附近精度牺牲较大。

针对上述问题，本文通过深入研究阻尼最小二乘算法的算法结构，开发了基于阻尼最小二乘DLS 法的逆运动学算法，提出了快速稳定的求解算法，并结合逆运动学求解后的关节角值，实现了轨迹优化后的关节速度，为后续进一步实现离线编程系统奠定算法基础。

1 机器人运动学分析

1.1 运动学模型建立

工业机器人是由各个关节刚体连接组成的，作为一种综合刚体，其自身各个关节运动满足一种位置和姿态关系，因此需要建立相关坐标系，以便用数学方法描述各个刚体间的位姿关系。在建立笛卡尔坐标系中，需要描述各个关节刚体的位姿关系，每个位姿关系都是四阶齐次变换矩阵，根据每个关节的齐次变换矩阵，得到机器人系统的位姿变换矩阵。

本文研究的对象是埃夫特公司的ER165 机器人，机器人机械如图1 所示。根据机器人坐标系建立原则，建立各个关节的坐标系，包括基座标系和末端坐标系，其坐标系如图2 所示。

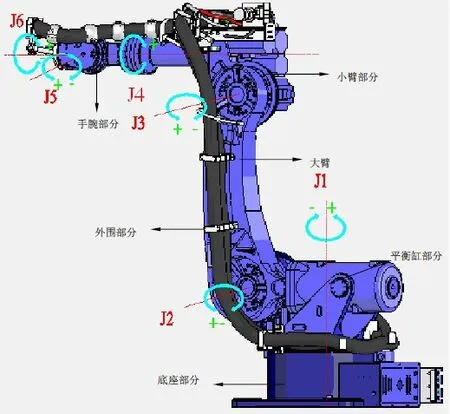
图1 ER165 机器人

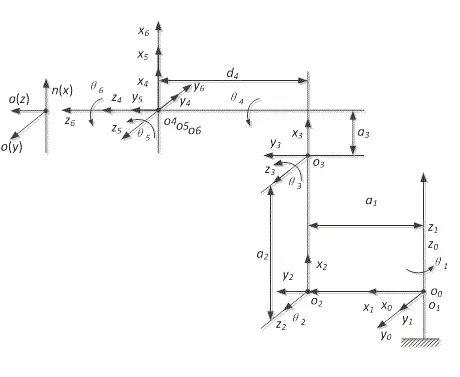
图2 D-H 坐标系

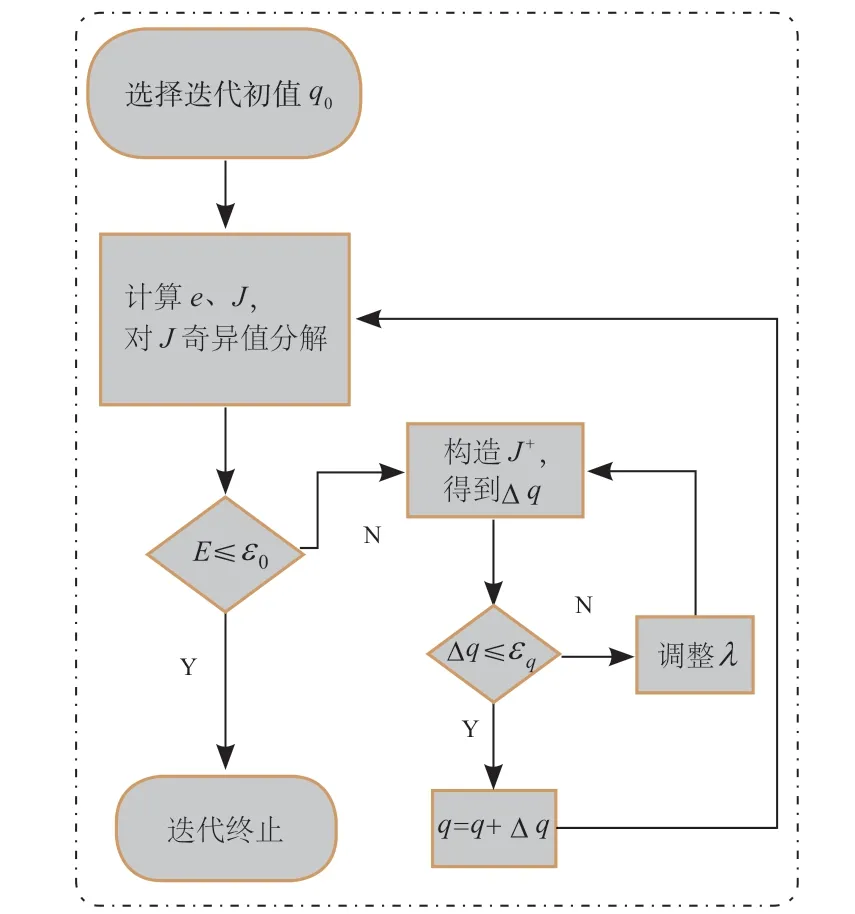
图 3 轨迹优化算法流程图

其D-H 参数如表1 所示。

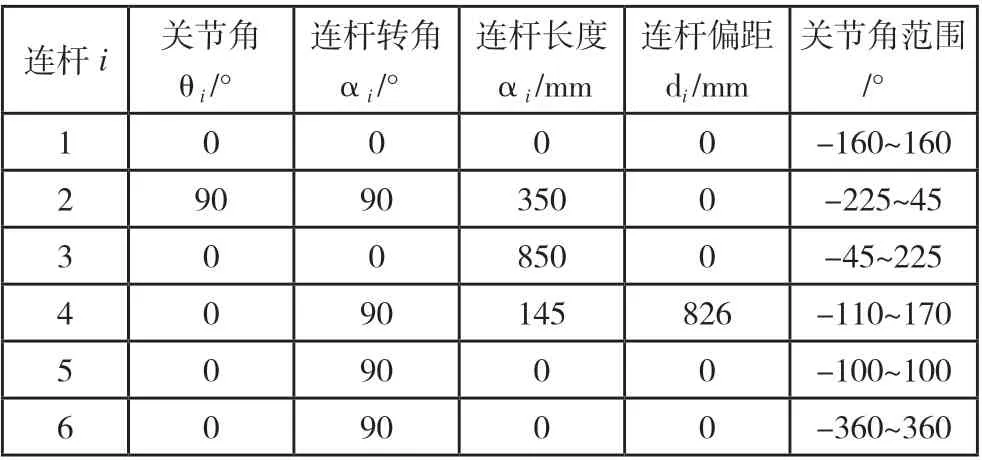
表1 机器人D-H 参数列表

通过 D-H 参数可建立其关节之间坐标系的齐次变化矩阵，及D-H 参数模型[11]；通过各连杆相乘可得机器人的变换矩阵 。

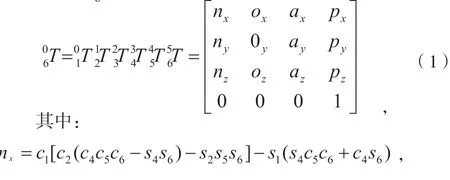
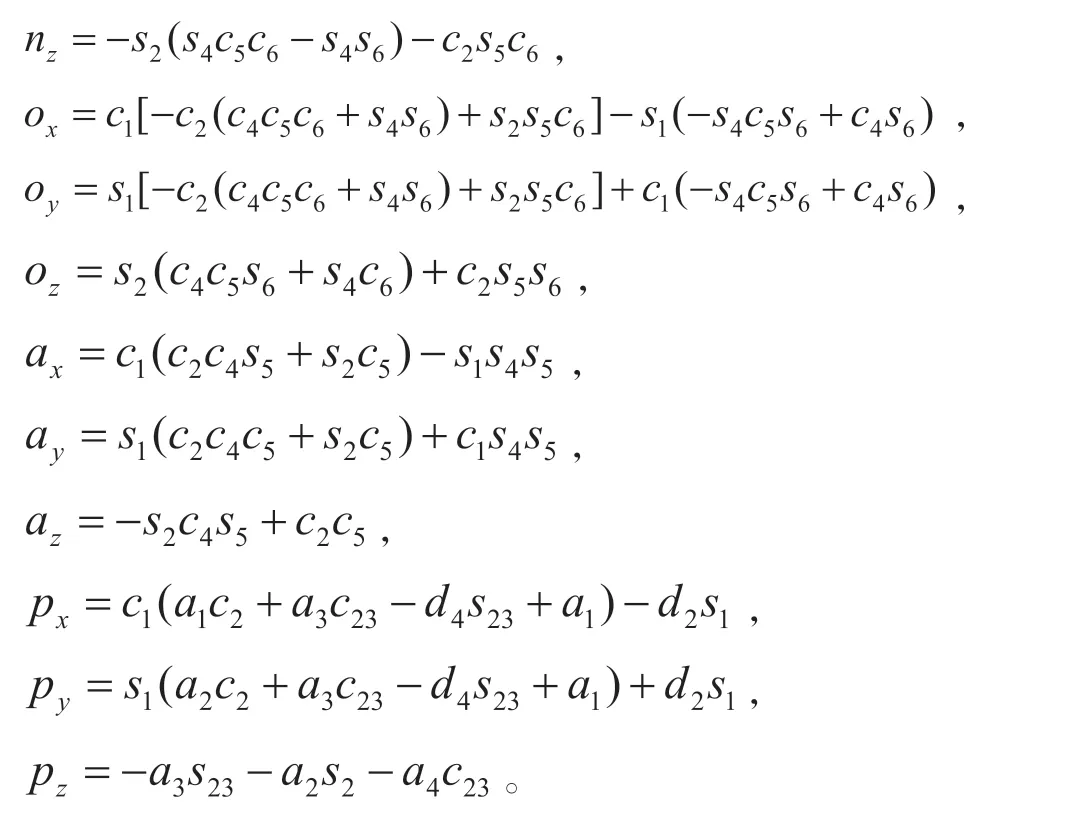
1.2 雅可比矩阵构建

雅可比矩阵[12-13]是描述机器人末端执行器在运动工程中速度与各关节速度之间变换的重要工具。当机器人在奇异点时，导致自由度丢失，造成雅可比矩阵的行列式为零，无法得到准确解，造成失速现象。

机器人运动过程中，用x表示操作空间的位移，q表示关节空间关节位移，利用运动方程来描述两者之间的映射关系：

2 奇异点规避算法研究

2.1 奇异点产生机制分析

奇异点具体主要有三种类型：第一种称腕部奇点，当5 轴为0°时，由于4轴和6轴是共线，导致雅可比矩阵无解；第二种称为肩部奇点，当2 轴、3 轴延长线与5轴在一条线上时产生；最后一种称肘部奇点，当4、5、6 轴交叉点处的腕部根节点正好位于1 轴上方时，则会产生奇异点。

当机器人处于奇异位置时，机器人末端做很小的位移，关节必须产生很大的运动速度，一旦机器人失去自由度，沿着运动轨迹的运动便容易造成碰撞等危险，导致机器人处于失控状态。

2.2 奇异点规避算法

由上述针对奇异点分析可知，奇异点的产生主要是由于当机器人处于奇异位，计算机在利用雅可比矩阵计算机器人速度逆解时不可解，导致速度丢失的现象。因此，本节基于阻尼最小二乘DLS 法的逆运动学算法，提出快速稳定的求解算法。

将式(3)转换为微分变量，并且规定末端执行器微分差为误差e，关节速度微分差为误差 ，得到：

表示的不全面，通过分析雅可比矩阵条件数的性质，本文提出另外一个指标即第二条件数 来描述机器人奇异性。因此，分别计算机器人的第一条件数 和第二条件数 ，根据雅可比矩阵的病态程度判断阻尼系数计算公式，调整阻尼系数因子的计算公式如下：

式（15）中， 、 、 、 为常数，通过计算第一条件数 、第二条件数 与给定阈值 、 的比较来确定阻尼系数 。

3 仿真流程和参数

3.1 仿真流程

在仿真实验中，主要通过对阻尼系数的实时调整，对轨迹进行优化。针对机器人模型，轨迹优化迭代算法步骤如下：

1）选择关节变量迭代初值，根据机器人逆解得到的值选择与最优解误差最大的值。

2）计算机器人雅可比矩阵并对其作奇异值分解，得

由流程图看出，通过对阻尼系数 进行自适应调整，对比 与 大小，寻找最优的阻尼系数实现精度和稳定性的平衡。

3.2 仿真参数

4 仿真结果分析

实验仿真轨迹如图4所示，其中圆圈位置表示奇异点。

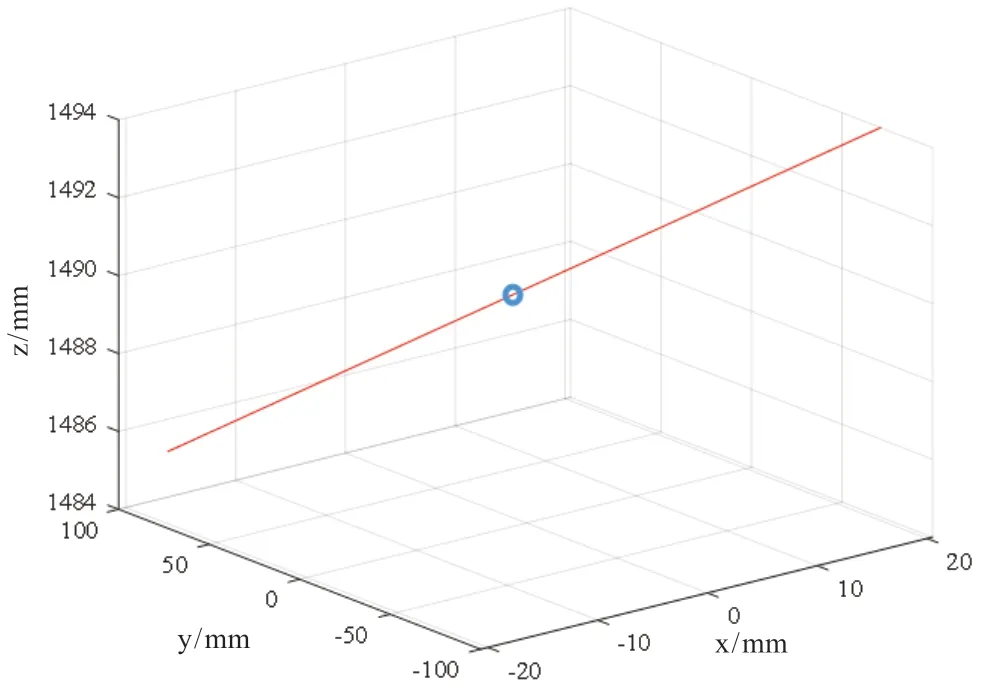
图4 仿真轨迹图

为了图像的简洁清晰，本文只展示出机器人4、5、6轴的速度曲线，仿真结果如图5、图6 所示，其中虚线代表4 轴，点画线代表5 轴，实线代表6 轴。

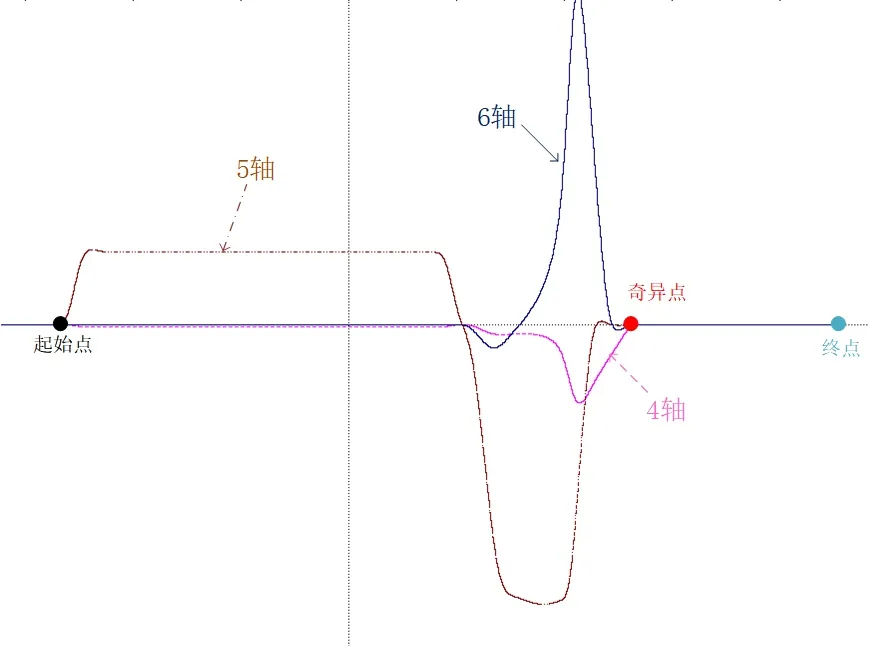
图5 改进前速度波变图

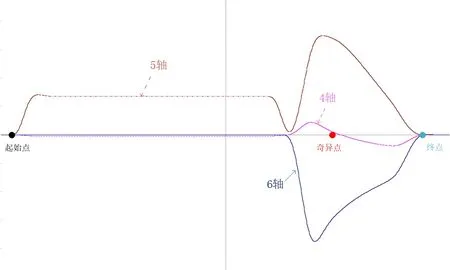
图6 改进后速度波变图

如图5所示，改进前机器人在奇异区域由于逆解无解，5、6 轴运动速度将会无限增大，反应至实际速度图像上，即5、6 轴在奇异点前速度突然变大，当轴速度超过设置极限时，由于机器人自身保护机制，轴速度逐渐降为0，从而导致停机报警。

图6 所示，5、6 轴在趋于奇异点区域时，运动速度逐渐增大，但没有超过设置极限，顺利到达终点。结果说明，本文算法可以使机器人避开奇异区域，使各轴运动速度平稳过渡，保证了运动的连续性。

5 结论

本文针对工业机器人进行运动时遇到奇异点问题，导致机器人停机、失控背景下，通过雅可比矩阵对奇异点产生原因分析，并对阻尼最小二乘算法结构深入研究，提出快速稳定的求解算法，结合逆运动学求解后的关节角值实现了轨迹优化。仿真结果显示，优化后的关节速度没有产生突变，运动速度在奇异区域过渡平稳，验证了本方法的可行性，为后续进一步完善离线编程系统奠定算法基础。