基于相似月和Elman神经网络的行业月度售电量预测

孙旺青，刘晓峰，何沁蔓

（南京师范大学 南瑞电气与自动化学院，南京 210023）

0 引言

近年来，我国电力事业快速发展，对电力系统的决策与规划的要求不断提高。作为电力系统的基础环节，提高售电量预测精度对电力系统平稳运行有着重要意义［1］：一方面，准确的售电量预测可以帮助电力企业合理规划发展计划、优化网络布局并提高电力系统运行的安全性；另一方面，售电量直接反映了地区经济发展水平，准确的预测结果可以为当地政府提供参考，进而制定相应的政策适应地区发展。

为了深层挖掘用电量的变化规律，提高电力预测精度，精细化区分用电负荷是一个研究重点。文献［2］从电力市场的角度出发，分析了纺织业的容量变化特征及业扩报装容量特征，根据影响纺织业变化的各项指标完成了对纺织业用电量的预测，但是该预测方法对预测对象的概率信息的准确度有较高要求，难以大面积推广。而文献［3］在预测过程中，使用的历史数据跨度为24 年，对于早期历史数据的有效性未作分析。文献［4］对陕西售电公司的海量数据进行分析，建立了一套统计各行业同期售电量数据的方法，对各行业的同期售电量进行预测，但是该方法对行业划分过于细致，不同行业之间存在交集，因此分类方法的针对性较低。文献［5］结合不同行业的用电特性，对日负荷曲线进行建模，提出了分级预测的方法，可以对居民、商业、市政、文娱等行业完成精准预测。

对大量历史数据进行分析处理，合理确定预测对象的影响因素可以显著提高预测精度［6—7］。文献［8］提出一种基于相似日的新型热气候指数矩阵与涵盖多特征因素的最大信息系数热环境评估方法，其中特征因素包括气象、地理区位等，有效提高了负荷预测的精度。文献［9］以海量数据为基础，提出一种并行局部加权线性回归模型，对大量数据进行处理，以15 min 为周期，考虑了各周期内最高温度与最低温度，该模型运算时间短，精度符合预测要求。文献［10］采用动态权值优化，增强了相似日选取算法的适应性和有效性，在选取相似日时，充分考虑了环境因素，如温度、湿度、降雨量，最后结合灰色模型完成了短期预测。文献［11］结合经验模态分解与特征相关分析，量化分解后的负荷分量和特征信息之间的相关性时，考虑了天气因素及电价变动对负荷量的影响，最后运用最小二乘支持向量机模型完成预测。文献［12］重点分析了重大事件因素对售电量预测的影响，包括异常高温、政治事件和超强台风，这些因素使实际售电量严重偏离预测曲线，但文中所提解决方法较为繁琐，需要根据不同事件逐个完成修正。

现有研究主要有如下一些不足：①由于售电对象包含各类用户，不同类别用户的用电规律都有所不同［13］，因此有必要对各类用户合理分类后单独完成预测，上述关于行业预测电量的文献［2］—文献［6］大多采用回归分析法，无法详细描述各种影响电量的因素，且模型初始化难度大；②售电量容易受GDP、地区经济发展状况、人口和气候等多种因素的影响［14］，有必要对影响售电量的众多因素做分析，上述分析电量影响因素的文献［8］—文献［12］以天气因素为主，较为单一。

针对上述问题，本文提出历史相似月和Elman神经网络相结合的月度售电量组合预测算法，并通过灰色关联度分析法［15］量化每个影响因素对预测结果的影响，对各类用户的售电量进行分类预测，挖掘不同用户的售电规律，最后利用MATLAB软件对某公司的历史售电数据进行分析并完成预测，验证本文所提出的组合预测方法的有效性。预测流程如图1所示。

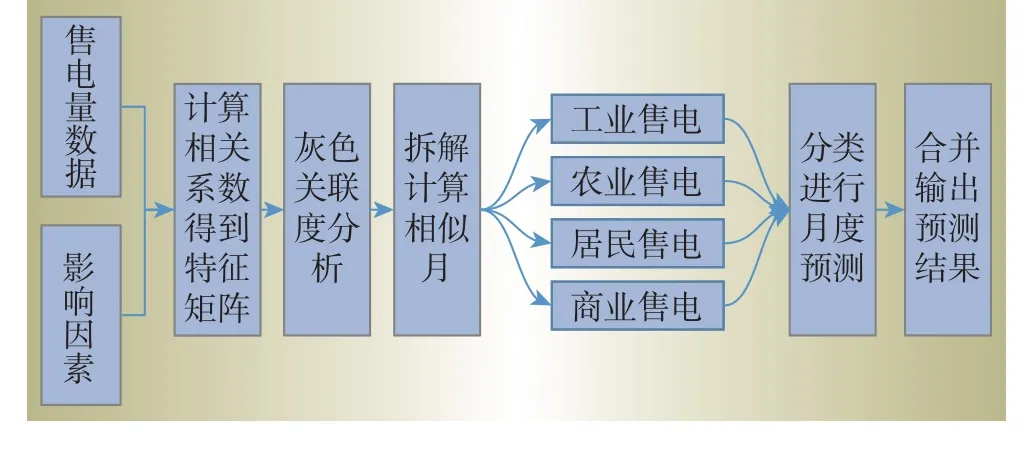
图1 预测流程Fig.1 Prediction flow

1 模型建立

1.1 相似月特征向量建立

历史样本和待预测月份之间各类信息的相关程度直接影响了预测结果的准确度，因此本文在相似日的基础上提出了相似月的概念。选取相似日时，由于时间跨度短，影响因素一般为气温、星期类型和节假日因素［16］，用户数量视为不变。但在选取相似月时，随着时间跨度的增加，用户数量的变化对售电量的影响也无法忽略。此外，由于不同月份之间时间跨度较大，气温的变化程度也更大，且不同类别的用户对气温的敏感程度不同，因此各类用户受气温变化的影响需要分类讨论。综上，本文将相似月影响因素定为气温-季节因素、日期差距因素、节假日因素、重大事件因素、售电对象数量5 个因素。依据这些因素得到月度售电量预测的相似度特征矩阵，用来表征历史月与待预测月的相似程度，本文将相似度特征矩阵Η表示如下

式中：α为气温-季节因子；β为日期差因子；δ为节假日因子；θ为重大事件因子；ε为售电对象数量因子。

1.1.1 气温-季节因子

为了分析气温-季节类型对售电量造成的影响，需要通过气温-季节因子α来衡量历史月和待预测月的相似程度。由于气温、季节因素对售电量的影响难以直接衡量，不同月份的气温、季节因素均有所不同，因此本文借助聚类的思想将月份分类。以农业售电量为例，首先将每年各月份的农业售电量完成归一化处理，再求出每个月份的均值，最后通过K-means算法将各月份分为低售电量、中售电量、高售电量月份3组后，用0.3、0.5、0.7依次标记作为气温-季节参数。该方法的具体流程如图2所示。

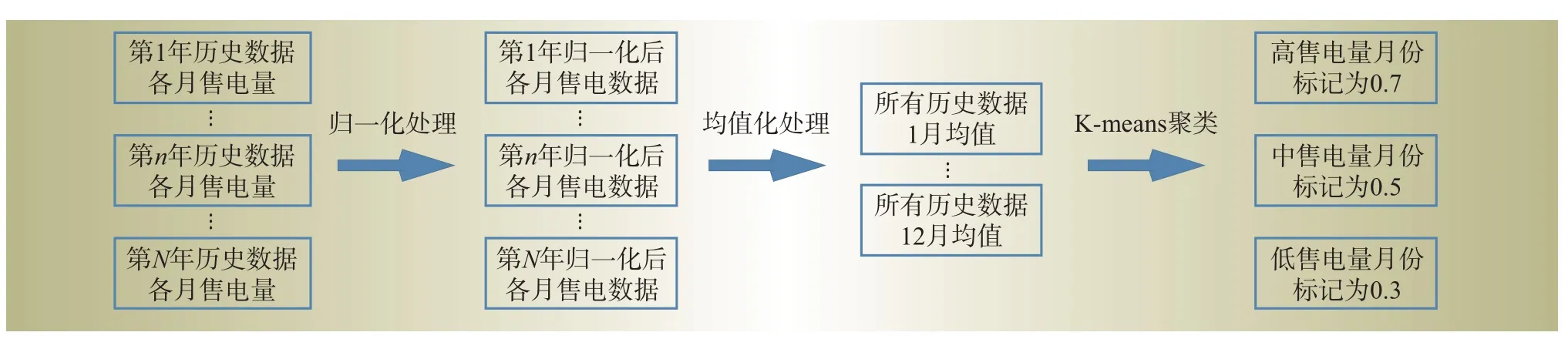
图2 气温-季节参数计算流程（以农业售电量为例）Fig.2 Calculation process of temperature-seasonal parameters（take agriculture for example）

气温-季节因子α表示如下

1.1.2 日期差因子

随着时间的推移，月度售电量会因为经济的发展而呈上升趋势。因此，如果样本数据的日期与待预测月的日期差距过远，那么样本数据的参考价值将会大大减弱，所以本文引入了日期差因子β来衡量历史月和待预测月之间日期的相似程度，日期差因子β表示如下

式中：fh和fp分别为历史月和待预测月节假日信息。当历史月和待预测月包含同一个节假日时，fh=fp，此时节假日因子δ=1，否则δ=0。

1.1.4 重大事件因子

各类用户的购电行为会因为重大事件出现波动，如持续高温、持续低寒、各类持续性突发事件等都会让该月的售电量高于或低于同期，因此需要通过重大事件因子θ来判断历史月与待预测月是否具有类似的重大事件，重大事件因子θ表示如下

式中：ch和cp分别为历史月和待预测月的重大事件信息。当历史月和待预测月有相同的重大事件时，cp=ch，此时重大事件因子θ=1，否则θ=0。

1.1.5 售电对象数量因子

售电总量与用户的数量有着密切的关系。对于每一类用户，采用售电对象数量因子ε来衡量这一相似性，售电对象数量因子ε表示如下

式中：μh和μp分别为历史月和待预测月该类售电对象的数量。

由于相似度向量5 个因子存在数量级上的差距，为了平衡各因子之间的权重，有必要对各影响因子进行归一化处理，本文采用极值归一化方法对各相似度因子进行处理，即

由于相似度特征矩阵中的5个影响因子对月售电总量的影响程度各不相同，本文利用灰色关联度分析法，计算各影响因子与售电量的关联度，并将结果作为该影响因素的权重，关联度越大则权重越大。此外，考虑到售电量在长时间尺度上处于长升的趋势，而影响因子中气温-季节因子、节假日因子和重大事件因子是处于以12 个月为周期的变化状态，本文在分析这3 个因子的关联度时，以12 个月为周期，分多次计算上述因子与售电量的关联度后取均值作为最终的结果，灰色关联度分析法具体过程如下：

式中：ρ为分辨系数，ρ越小，分辨能力越大，此处取ρ=0.5。

根据式（16），可获得相似度因子集合S=[s1,s2,…,sN]，从集合S中选取出若干与待预测月份相似度最高的历史月，即可作为待预测月的历史相似月。

1.2 Elman神经网络

Elman 神经网络属于动态递归神经网络，相比于BP神经网络，Elman神经网络在隐含层增加一个承接层，通过存储内部状态使其具备映射动态特征功能，系统因此具有时变特性，增强了网络的全局稳定性，在计算能力及网络稳定性方面都比BP神经网络更胜一筹。Elman神经网络为4层结构，包括输入层、隐含层、承接层和输出层，其中承接层可以存储隐含层的状态信息，因此网络处理动态信息能力较优。Elman 神经网络的输入层、隐含层和输出层表示形式分别如下

建立Elman神经网络，其中网络的输入层共有5个节点，输入量为筛选出的目标类别用户历史相似月的各参数，包括气温-季节因子、日期差因子、节假日因子、重大事件因子和售电对象数量因子；输出层有一个节点，输出的目标值为目标类别用户当月的预测电量；隐含层的节点数量难以直接获得，因此本文针对不同种类的售电对象，用多组隐含层节点数量来测试网络的精确性，对比测试结果，选取精度最高的隐含层节点数量，见3.1节。在Elman神经网络的训练学习过程中，历史月的售电量数据作为目标输出值，网络内部完成权值的修正来提高训练精度。

2 实例分析

为了验证本文提出的组合预测方法的准确性和有效性，根据某省公司2016 年1 月至2019 年10月的数据作为样本数据，预测2019 年11 月和12 月的售电量数据。模型参数取值如下：衰减系数λ1=λ2=0.95，Y=12,N=46，分辨系数ρ=0.5。本算例采用的是Inteli5-8265U1.6GHz CPU 和8GB RAM的PC平台进行分析。

2.1 相似月的选取

为了寻找合适的历史数据作为Elman神经网络的训练集，以2019 年11 月的居民售电量的相似月为例。该类别的历史相似月选取结果如表1所示。

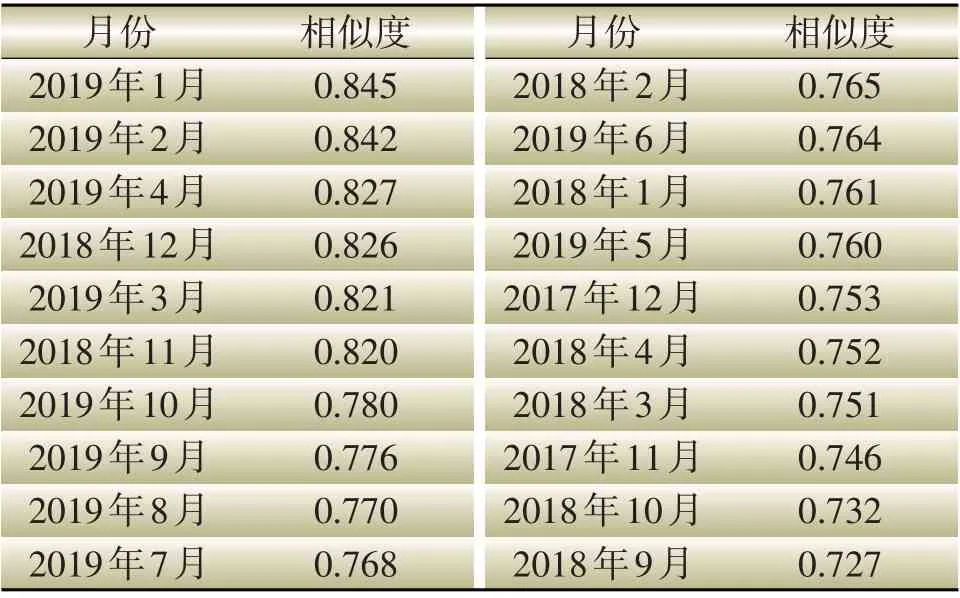
表1 2019年11月的居民售电的相似月选取Table 1 Similar month choose of residential electricity sales of November 2019

2.2 预测结果分析

Elman神经网络中隐含层节点数量没有准确的计算公式，依赖于经验，因此本文在预测时，选取多组节点数量对比预测结果。以2019 年11 月居民售电量预测为例，图3 给出了不同隐含层节点数时得到的不同的预测结果。从图4 可以看出，当隐含层节点数量为7时，预测精度最高。所以2019年11月居民售电量预测时隐含层节点数取值为7，全部取值结果如表2所示。

表2 隐含层节点数Table 2 Number of hidden layer node个

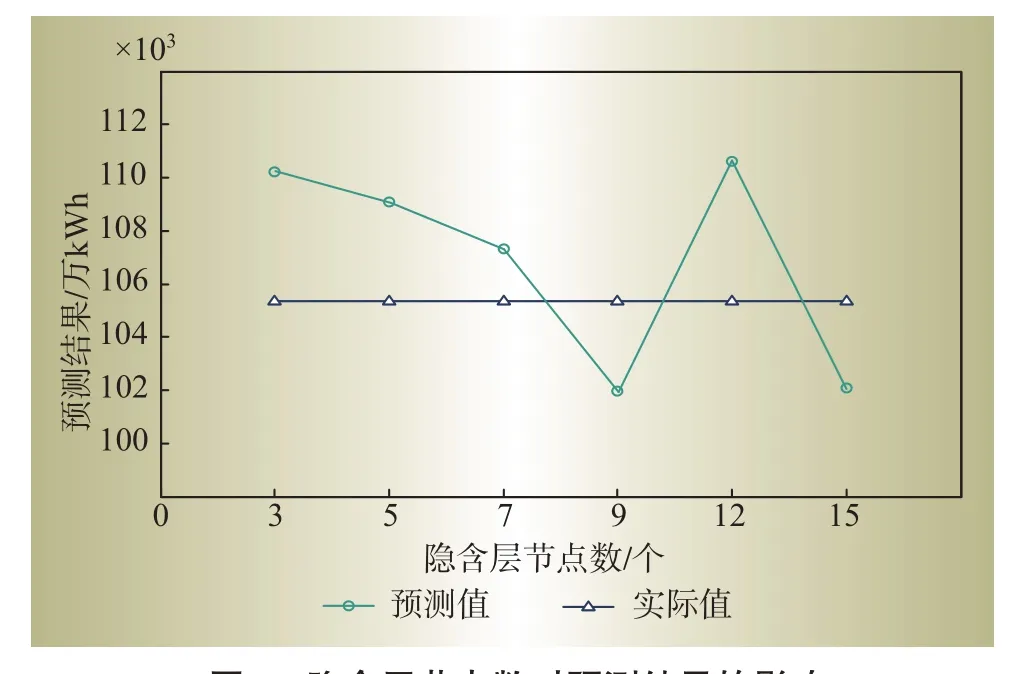
图3 隐含层节点数对预测结果的影响Fig.3 Effects of hidden layer node number on prediction results

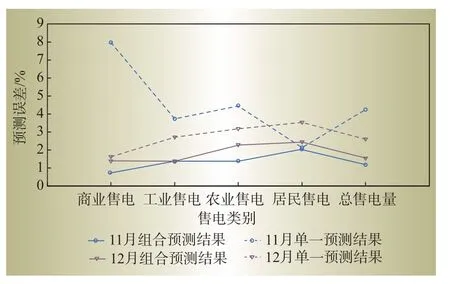
图4 两种模型的误差对比Fig.4 Error comparison between two models

将寻找到的相似度较高的月份信息作为训练样本，选取各自的隐含层节点数后，分别完成对2019 年11 月和12 月各类用户的售电量预测，预测结果如表3 所示。从表3 可以看出，各类预测结果都有较高精确度，最大误不超过3%，满足工程应用要求。

表3 预测结果Table 3 The predicted results MWh

为了验证本文提出的组合预测模型的实用性，图4给出了不考虑相似月信息的单一Elman 神经网络的预测误差对比。从图4 可以看出，组合预测模型在选取合适的训练集后，预测精度相比于单一的Elman神经网络有着显著的提高。

对两种模型的性能分析采用均方根误差（RMSE）和平均绝对百分比误差（MAPE）来衡量，指标表示如下

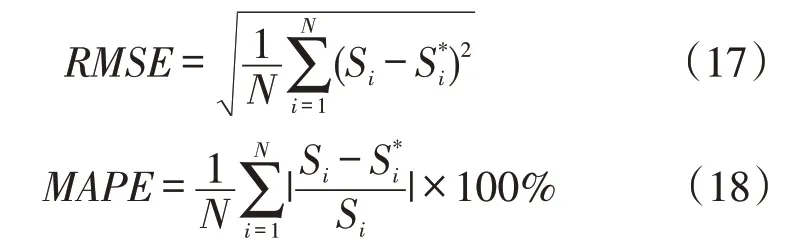
表4 模型误差分析Table 4 Model error analysis

3 结束语

本文提出历史相似月和Elman神经网络相结合的月度售电量组合预测算法，并通过灰色关联度分析法量化每一个影响因素对预测结果的影响。历史相似月模型可以在海量数据中快速提取出与预测对象具有相似条件的历史数据，大大提高预测精度。Elman 神经网络可以任意精度逼近任意函数，降低了模型复杂程度。相比于BP 神经网络，Elman神经网络具有动态特性好、逼近速度快、精度高的优点。结合这两种方法得到组合预测模型具有以下优点：

（1）充分考虑地区经济状况、人口和气候等因素的影响，可以对影响月度售电量的众多因素分析。

（2）对不同种类的用户分类进行了月度售电量预测，充分考虑了不同用户的售电规律。

本文提出的组合预测模型在收敛速度、预测精度等方面比单一预测模型都有较大提高，具有较强的实用价值。D