准确把握学情 科学实施教学
李凌云 李国良

【摘 要】本文通过对教材的调整与整合,科学研判学生的认知基础,两次运用有效的异同点的比较,使学生對三角形从角和边的角度进行更加准确的分类,并能在分类的过程中明确各类三角形之间的关系,运用联系的观点加深学生对三角形定义、类别的理解,使课堂教学更为精准、有效。
【关键词】准确 学情 分类
一、课前慎思
实施精准教学要根据课标的要求和学生发展的实际,全面研判教材的编排体系,遵循学生的认知规律,准确把握教学目标和教学内容,从而有效建构起教学结构。人教版数学 “三角形”单元涉及三角形的认识与特性、三边关系、分类及三角形的内角和与多边形内角和等知识点。基于学情,我们认为,对于这样的编排,在课时安排上可以做一些调整,一是在学习三角形的底和高时,需要运用到三种不同类型的三角形,特别在对直角三角形与钝角三角形高的认识与画高时,学生存在着较大的困难;二是在一年级时,学生已经认识了三角形,知道了三角形由三个尖尖的点、三条直直的边、三个角组成,也就是说,四年级学生是比较容易理解三角形的定义的,而三角形的分类也是认识三角形的重要组成部分,它们的共性就是三角形的定义,不同点就是角与边的大小、关系等。
笔者以为,可以把“三角形分类”结合在“三角形认识”一节课中,把教材中的“三角形的特性”安排在“三边关系”中,而把“底和高的认识”单独成立一节课。这样,学生对三角形的认识、分类会更加深刻,对三角形的稳定性认识、底和高的学习会更加到位,从而更加完整与全面地认识三角形。
二、基础慎析
学情基础是在开展教学前通过不同的调查方式对学生的知识水平、已有经验、思维能力等方面进行了解、分析与思考,为教学设计、实施有针对性教学等提供依据。
(一)调查内容的拟定与思考
基于对教材的分析与调整,结合“三角形认识与分类”的教学内容与要求,笔者根据思维发展水平层次设计了5个问题,旨在了解学生关于三角形的知识储备、分类标准、图示表征、深度理解等能力水平。
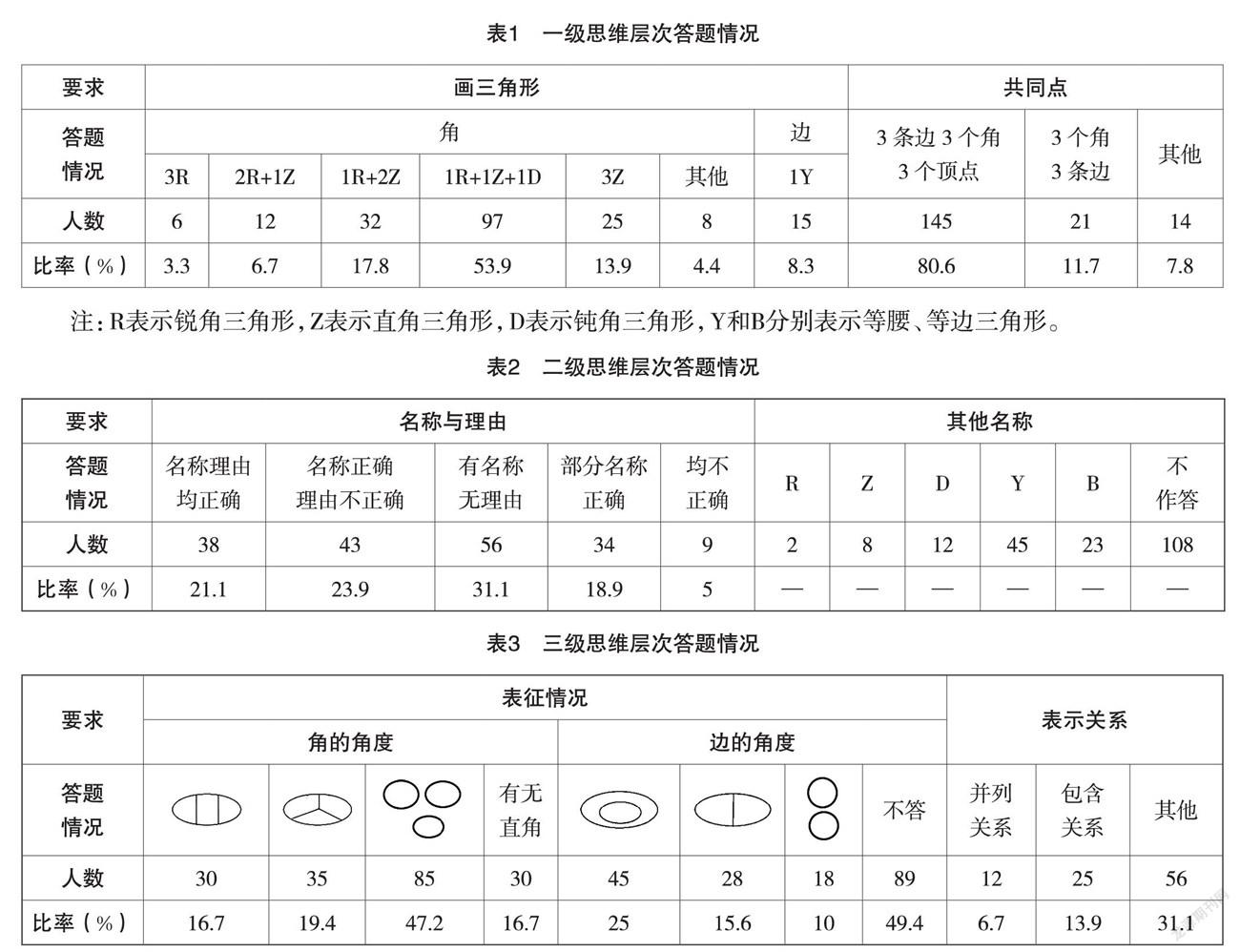
一级思维层次。本层次涉及两道题目,一是要求画出3个不一样的三角形,二是寻找3个三角形的共同点。主要考查学生能否从平时接触的三角形(三角板)中画出三类三角形,初步了解学生对三角形的共性与个性的把握程度,为后续分类做准备。
二级思维层次。本层次有两道题目,一是给画出的三角形取个名称并说说理由,二是除上述名称外,还知道哪些三角形。主要了解学生能否从角或边的特征来抽象出三角形的名称及对已掌握的三角形的名称的理解程度。
三级思维层次。本层次设计了一道题目,表征出三角形的类别和它们之间的关系。主要调查学生对三角形分类的掌握情况,特别是按角的特征与按边的特征进行分类后的关系图,了解学生的表征能力及对三角形分类本质的理解力。
(二)调查结果的梳理与分析
本次调查,选择了两所小学各两个班级的180个四年级学生进行前认知的调查,要求独立完成,用时10分钟。根据上述思维层次,笔者进行了梳理与统计,具体见表1、表2、表3。
从上述统计可以看出:
(1)大部分学生能从不同的角度画出不一样的三角形,53.9%的学生分别画出了按角分类的三类三角形,其中锐角三角形占多数,钝角三角形相对较少;而从边的角度画出等腰三角形的学生只占8.3%。画等边三角形有一定难度,因此,没一个学生能画出来,这说明如果不刻意强化边的长度,学生很少会想到等腰三角形或等边三角形,这说明三角形角的特征对于学生来说更加直观一些、本质一些。
(2)大部分学生能根据画出的三角形说出名称,但基本停留于锐角三角形、直角三角形和钝角三角形上;阐述理由方面正确率较低,特别是锐角三角形,18.9%的学生表述成有锐角的三角形叫作锐角三角形。对于等腰三角形和等边三角形,分别有45人和23人说到,说明学生还是知道涉及边的三角形名称,只是在画的过程中较少呈现从而无法阐述理由。
(3)从角的分类情况看,83.3%的学生能分清楚三类三角形,远远高于从边的角度来分析三角形。而对于从关系的角度来厘清三角形之间的区别与联系,学生在认知上存在困难。
分类既是一种数学活动,也是重要的数学思想,而分类后通过对事物之间关系的分析既能厘清其联系也能分析其区别。学生要正确掌握从角和边两个维度来进行分类并理解各种三角形之间的关系,需要了解一类事物的共同特征和性质,再进行相似类之间的比较,也就是先寻找共性再找异相。笔者认为,教材内容的调整与整合是合理的,可以加深学生对三角形更立体化的认知,在学生自行画三角形的过程中找到共性的特征:由三个点、三个角、三条边首尾连接的平面图形。然后寻找每一个三角形的个性特征,可以从角或边的角度进行分析,最终找到不同类三角形之间的联系与区别。当然,在研究三角形分类时,学生往往会从“角”的角度展开,这样显得更加本质一些。
三、实践慎行
人类认识事物必须经历两项活动,一项是对事物进行分类,一项是对每类事物进行度量。没有这两项活动的展开,学生就很难认清研究对象的性质、特征。因此,通过“三角形认识”前对其概念的全面了解与分析,我们采取了两次比较的方式让学生分别从角和边的角度来认识三角形。学生知道按角分有锐角三角形、直角三角形和钝角三角形,它们存在着并列的关系;按边分有一般三角形、等腰三角形、等边三角形,它们存在着包含关系。这样分类有利于更精准地开展教学,使学生更深刻地认识三角形的特征。
(一)基于比较理解三角形分类中的并列关系
概念是思维的基本形式之一,它需要把客观事物一般的、本质的共同特征反映出来,没有概念就难以对事物进行判断、推理与论证。课始,笔者组织学生画三个自己认为不一样的三角形,把与众不同的三角形贴在黑板上(如图1),并设疑:这些图形为什么都称为“三角形”。学生通过讨论得出,这些图形的共同特征是由三条线段围成,而且相邻两条线段的端点首尾相连。三角形的定义在寻找共性中自然而然地被抽象出来。
随后,教师提问:“这些展示的三角形有什么不一样吗?”
生1:有的三角形是直的,有的三角形是斜的。
生2:有的三角形有直角,有的三角形有钝角,有的三角形只有锐角。
生3:有的三角形有一个直角、两个锐角,有的三角形有一个钝角、两个锐角,有的三角形有三个锐角。
师:如果让你给这些三角形分类,你准备怎么分?说说理由。
生1:可以分两类,③④是有直角的三角形,其余是没有直角的三角形。
生2:可以分三类,①⑥是有钝角的三角形,③④是有直角的三角形,②⑤⑦是有锐角的三角形。
生3:同意生2的观点,但不是把有锐角的三角形归为一类,而是把有三个锐角的三角形归为一类。
……
接着,大家一起讨论分成三类的理由,并用图的形式把它们之间的关系表征出来。这一寻找共性与个性的教学,正是基于调查结果的运用。学生在画三角形的过程中,很少会从边的角度去画等腰三角形与等边三角形,自然不会想到从等腰三角形与等边三角形上进行分类,这样可以更加本质地从角的关系上进行三角形的分类。
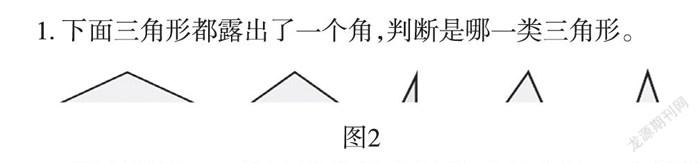
在此基础上,笔者要求学生进一步寻找这些三角形的共同特征,那就是每个三角形都有两个锐角。在学生掌握三类三角形的定义后,笔者出示图2,要求根据定义来判断,进一步巩固钝角三角形与直角三角形最大的特征是有一个钝角和一个直角,判断锐角三角形必须明确有3个锐角。
图2
笔者以为,二分法是分类中最基础的方法。在前测与实际的教学中,部分学生容易以直观的感知介入分类。此时,教师要大胆地引导学生进行讨论、分析,从三角形显著特征——角來明确分类,逐渐地按照同一标准分,使学生知道其结果也是唯一的,从而懂得以角为标准将三角形分为锐角、直角、钝角三角形三类,它们之间的关系是并列的,均属于三角形中的一种。
(二)基于度量感悟三角形分类中的包含关系
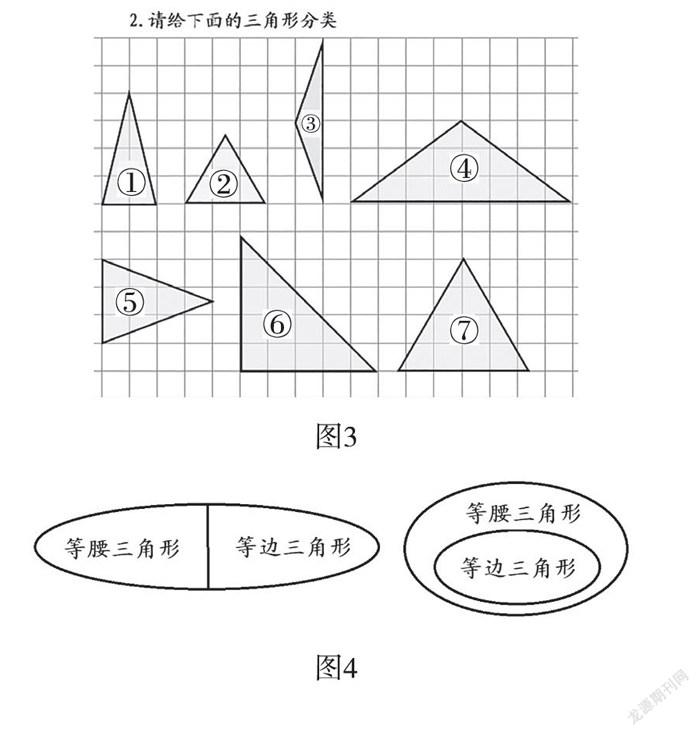
有了上述分类基础后,笔者出示图3,要求学生对这些三角形进行分类。很快,学生把①②⑤⑦归为一类(锐角三角形)、③④归为一类(钝角三角形)、⑥为一类(直角三角形)。教师设疑:“这些三角形有什么共同特征?”学生通过分析、讨论,一致认为它们都是轴对称图形,接着,学生进行度量、验证,发现①③④⑤⑥有两条边相等,而②⑦有三条边相等。明确有两条边相等的三角形叫作等腰三角形,三条边都相等的三角形叫作等边三角形。在厘清分类标准,知道顶角、底角、腰的概念后,教师组织学生对等腰三角形与等边三角形的关系进行表征,于是出现图4的两种情况。
生1:因为三角形也可以分成等腰三角形与等边三角形,赞成前面一种。
生2:后面一种的关系图还可以,等腰三角形是两条边相等,而等边三角形是三条边相等,这样的图让我想到了正方形是特殊的长方形。
经过集体讨论,教师呈现出从边的角度来研究等腰三角形与等边三角形及一般三角形的关系,让学生懂得按边的关系来分析等腰三角形是特殊的三角形,而等边三角形又是特殊的等腰三角形,它们是包含关系。
笔者以为,呈现出图3这道题目,不仅可以让学生巩固按角分类的知识点,而且不经意间引导学生从轴对称图形的维度来分析三角形,从而把观察点落到边的角度进行分析。一个好的学习素材,不仅能聚焦数学知识的本质,还能提高课堂教学效率,达到事半功倍的效果。
接着,教师再次组织学生分析图3,设问:“做了这道题目后,大家有什么想法?”
生1:如果从三角形的角来看,这些三角形可以分成三类;如果从边的角度看,这些三角形可以分成两类。
生2:从角进行分析,所有的三角形有锐角、直角、钝角三角形三类;从边进行分析,有一般三角形和特殊的三角形。
关于三角形的分类,我们不仅可以从角的维度去思考,还可以从边的角度去分析。通过这一梳理与总结,学生体会到一个事物可以从多个不同的角度去认识,但一定要选择合适的标准,才能对事物进行合理的分类。学生真正感悟到“换个角度看数学,一样的数学不一样的内涵;换个角度看世界,一样的世界不一样的精彩”。
课标指出,课程内容的选择要贴近学生的实际,有利于学生体验与理解、探索与思考。从初设教材的整合到学生认知基础的调查,再进行课堂教学验证,教师基于精准化课堂教学理念来改进教学方式与行为,使教学内容更加符合学生的认知规律,更能提升学生对数学概念本质属性的认知,逐渐地使思维从感性走向理性。

