基于ARIMA与LSTM的海岸带地面沉降预测方法——以杭州湾地区为例

朱 宝，罗孝文，吴自银

(1.上海交通大学海洋学院，上海 200240；2.自然资源部海底科学重点实验室，浙江 杭州 310012；3.自然资源部第二海洋研究所，浙江 杭州 310012；4.自然资源部海洋空间资源管理技术重点实验室，浙江 杭州 310012；5.浙江省海洋科学院，浙江 杭州 310012)

0 引言

海陆过渡带是陆地与海洋之间的交界地带，其中包含了复杂的物理过程、化学过程、生物过程以及地质过程等，因而这里成为了地球表面动态环境最复杂多变的区域之一。目前海陆过渡带区域生活着数十亿人，是世界上最繁荣发达的区域之一，其演变过程与人类的可持续发展直接相关，该区域受到全球各个沿海国家的高度关注。

地面沉降是指地下支撑物的移动导致地面标高损失的一种地质灾害[1]，它是自然因素与人为因素共同影响的地质过程。其中自然因素包括构造下沉、地震及火山活动、气候变化等，人为因素包括开采地下水、油气资源、矿产资源等。海陆过渡带区域的长期地面沉降累积，会导致洪涝灾害的加剧、建筑物寿命的缩短以及交通网络的损失等[2]，这些都会严重威胁到人们的生命财产安全。因而有效监测地面沉降并给出相应的预警信息十分必要。杭州湾地区为典型的海陆过渡带，其围垦历史悠久，存在着地面沉降现象[3]，本文选择了该区域进行地面沉降预测研究。

地面沉降监测方法主要有水准测量、GPS(Global Positioning System, 全球定位系统)测量以及InSAR(Interferometric Synthetic Aperture Radar, 合成孔径干涉雷达)测量等[4]。其中InSAR技术具有全天时、全天候、高精度、实时性、连续性等优点，广泛应用于陆地地面沉降的监测。例如，王超 等[5]和廖明生 等[6]分别利用该技术得到了苏州市和上海市地面沉降的分布情况，精度均达到了毫米级。但针对海陆过渡带复杂多变的情况，如何利用InSAR时序数据对地面沉降进行预测的相关工作开展得还不够。

地面沉降预测方法，主要有基于物理机制的方法、基于数理统计的方法以及基于机器学习的方法等[7]。基于物理机制的方法需要大量的实地监测数据，提出基于岩石、水文特性演化的物理模型，并对大量复杂参数进行求解，并且受到时效性的严重影响；基于数理统计的方法则是根据大量历史测量数据得到统计规律，并进一步进行分析；基于机器学习的方法是从更高的数据维度提取现有历史数据的特征，进而得到对现有数据的反馈，不会受限于物理参数的影响[7]。

上述预测方法，其本质是对于时间序列的预测问题，主要的模型[8]包括：传统的ARIMA模型(Auto Regressive Integrated Moving Average model，差分整合移动平均自回归模型)[9]，机器学习的支持向量机[10-11]、贝叶斯网络[12]、矩阵分解[13]、高斯过程[14]、深度学习等[15-23]。

由于海陆过渡带动态环境复杂多变，在对InSAR数据得到的地面沉降时间序列进行单一预测模型处理后，得到的预测效果并不理想。为此，本文提出了一种混合了ARIMA和深度学习中的LSTM(Long Short-Term Memory, 长短期记忆单元)的预测方法，即对InSAR得到的形变量时间序列与ARIMA方法得到的预测时间序列作差，然后利用LSTM对得到的时间序列差值进行学习，并把LSTM模型预测的结果加在ARIMA预测数据上，即可得到原始InSAR形变量时间序列的预测结果。本文使用杭州湾部分地区2017—2019年的地面沉降InSAR监测数据进行时间序列建模来对此方法进行验证，结果表明，该混合预测方法相对单一预测方法的精度有显著提升。

1 方法原理

本文所采用的方法流程如图1所示。InSAR的SLC(Single Look Complex, 单视复数)影像数据首先经过欧洲航天局的SNAP(SentiNel Application Platform)软件预处理，得到干涉图；然后利用StaMPS(Stanford Method for Persistent Scatterers)得到特定点的时间序列；接着利用ARIMA方法进行初步预测，与原始序列作差，并利用LSTM对该差值序列进行学习，以改进ARIMA方法的误差项；最后在此基础上进行预测。

图1 混合ARIMA和LSTM方法时序预测流程图

1.1 基于StaMPS方法的InSAR数据处理

StaMPS方法是由HOOPER et al[24]发展而来的一种从合成孔径雷达采集的时间序列中提取地面形变量的算法软件包。相比于传统的PS-InSAR(Persistent Scatterer Interferometric Synthetic Aperture Radar,永久散射体合成孔径干涉雷达)选取永久散射体点的方法，StaMPS方法的选取规则可以识别散射强度较低但稳定性较高的目标，可以改善在非城镇地区传统PS-InSAR方法选取PS(Persistent Scatterer,永久散射体)点不足的情况[25]，更加适用于海陆过渡带区域。

干涉相位图的相位组成如式(1)所示：

φ=W{φdef+φatm+Δφorb+Δφθ+φN}

(1)

式中：φdef代表地形变化相位，φatm代表大气延迟相位，Δφorb代表残余轨道误差相位，Δφθ代表残余视向角误差相位，φN代表噪声相位。所有这些相位纠缠在一起构成了干涉相位图的相位信息[24]。

StaMPS利用了三维解缠算法，在时间上计算每个PS点的相位差异，然后设置参考点用最小二乘法在空间上进行解缠[26]，相比于传统的方法精度更高。

解缠后的相位通过时间上的高通滤波，空间上的低通滤波，得到大气延迟相位并将其减去，从而矫正了大气误差。最后经过相位反演得到形变信息。

1.2 ARIMA方法

经典的时间序列预测模型包括自回归模型(Auto Regressive, AR)，移动平均模型(Moving Average, MA)，以及两者相结合的自回归移动平均模型(Auto Regressive Moving Average, ARMA)[8]，进一步利用差分运算，就得到了ARIMA模型。AR(p)模型如式(2)所示，MA(q)模型如式(3)所示，ARMA(p,q)模型如式(4)所示[8]：

(2)

(3)

(4)

式中：Xt是t时刻的随机变量，αi和βi是权重系数，p和q表示时间窗长度，εt则代表了t时刻的白噪声。

上述3种模型是弱平稳的，适用于平稳时间序列预测，若涉及到非平稳时间序列，则需要结合差分运算得到平稳序列后再进行预测，即ARIMA模型。经过实验比对，ARIMA模型的预测误差稳定性较好[27]，可以用于后续与InSAR数据作差，进而使利用LSTM进行残差序列学习结果的收敛性得到保障。

1.3 LSTM方法

循环神经网络(Recurrent Neural Network, RNN)是一种能够将当前的数据与之前的数据建立联系的深度神经网络。但由于非线性函数的存在，其中离现在数据较远的数据会受到梯度衰减的影响，进而造成梯度消失问题；如果离当前数据较近的数据记录过多，会造成梯度爆炸问题。

为解决RNN的潜在问题，LSTM模型被提出[28]，它继承了RNN的记忆性，并增加了门控制单元对信息进行取舍，然后经过反向传播的梯度调整，从而完成模型的建立。其中以隐藏层最为重要，它由多个细胞单元组成，其细胞单元结构如图2所示。

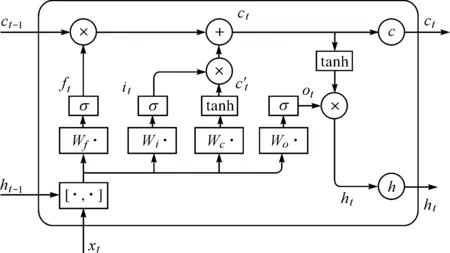
图2 LSTM隐藏层细胞结构

每个细胞单元中含有3个控制门，分别是遗忘门f、输入门i以及输出门o。其中，遗忘门决定了上一时刻的细胞单元状态ct-1有多少成分保存到ct中；输入门决定了当前时刻输入的xt有多少成分保存到ct之中；输出门决定了ct中有多少成分被传递到ht之中。从输入到输出的方向上的前向计算方法为

ft=σ(Wf·[ht-1,xt]+bf)

(5)

it=σ(Wi·[ht-1,xt]+bi)

(6)

ct=ftct-1+ittanh(Wc·[ht-1,xt]+bc)

(7)

ot=σ(Wo·[ht-1,xt]+bo)

(8)

ht=ottanh(ct)

(9)

式中：xt表示t时刻该细胞单元的输入，ct表示t时刻该细胞单元的状态，ht表示该细胞单元的隐藏层输出，W和b分别为对应的权重系数矩阵和偏置项，σ和tanh分别为sigmoid函数和双曲正切激活函数。

LSTM的模型训练过程与循环神经网络一致，通过反向传播方法计算误差项δ，然后根据误差项计算每个权重的梯度，进而利用梯度优化算法更新权重完成训练。

1.4 利用LSTM对ARIMA的残差序列进行学习的预测方法

假设利用StaMPS方法得到若干个PS点，每个PS点对应的形变量时间序列记作{Yt}，其长度为T。

(10)

(11)

利用LSTM模型对上述标准化残差序列进行训练。设测试集的长度为Ttest，训练用时间序列长度为L。实践表明，单步预测的误差是最小的，因而对时间序列进行标注，使其成为监督数据时，只需要最后一个作为标签即可。故训练用的样本输入为(L-1)个。

LSTM的主要参数包括训练用时间序列长度L，神经网络层数K，隐藏层神经元个数N，训练次数epochs以及学习率η。可以采用网格搜索法得到最优参数，同时采用随训练次数增加逐步衰减的学习率。

确定LSTM参数后，可以开始对其进行训练。采用ADAM优化算法[29]，设定损失函数loss为绝对误差：

(12)

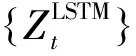
(13)

(14)

(15)

(16)

式中：RMSE表示均方根误差，MAE表示平均绝对误差，MAP表示平均实际绝对量，μ表示平均预测精度。

2 结果与分析

2.1 数据及预处理

选取杭州湾部分区域(30°00′—30°30′N, 120°45′—120°55′E)为研究区。由于水准数据采用的是杭州湾南侧的绍兴市上虞区数据，故通过相对稳定的嘉绍大桥沟通南北两岸，以验证杭州湾北侧的形变数据的准确度。经过与分布于研究区的水准点测量数据对比，本文所采用的InSAR方法得到的结果精度达到毫米级，可以满足研究需求。

以2017年1月至2019年12月获取的Sentinel-1A影像的上升轨道、VV极化方式的SLC影像为遥感数据源，利用PS-InSAR技术选取2018年7月16日的影像作为主影像，共得到配准的主、副影像干涉图83幅，主、副影像的时间基线以及空间垂直基线的关系如图3所示。

图3 主、副影像时间基线与空间垂直基线关系

利用StaMPS方法筛选，共计得到274 926个PS点，进一步得到沿雷达视线方向的地形变化时间序列，其中每个点拥有83个形变记录，其年平均形变量及其叠加在卫星图上的情况如 图4 所示。从图4可以看出，沿杭州湾两岸地形整体呈现相对下降的趋势，而处在更靠近陆地的位置则在整体上呈现出相对上升的趋势。

图4 研究区年平均形变量

对所有PS点的形变量数据、年平均形变量数据做统计分析。3年时间内，该地区的形变量在-71.98～90.25 mm范围内，年平均形变量为-23.65～10.93 mm/a。图5a代表了所有PS点的形变量数据分布情况，绝大多数形变量数据集中在-20～20 mm之间；图5b 为年平均形变量直方图分布，年平均形变量大多集中在-10～5 mm/a的范围内。

图5 所有PS点的形变量(a)以及年平均形变量(b)分布直方图

2.2 模型预测结果

针对地面沉降漏斗区域的监测情况，选取两处地面沉降较为明显的PS点，分别利用ARIMA、LSTM以及ARIMA-LSTM三种方法进行预测以及对比。在 图6 中用深蓝色框标注了选取的两个点，并分别命名为A和B。采用最大似然估计得到ARIMA的最优参数，用网格搜索法得到LSTM的最优参数。ARIMA方法的(p,d,q)参数最终选择为(5,1,0)；LSTM方法则按照时间先后顺序划分训练集以及测试集，2017年和2018年的数据作为训练集，2019年的数据作为测试集，epochs次数为100，隐藏层神经元个数为10个；ARIMA-LSTM方法以2019年的前2/3年数据作为训练集，后1/3年数据为测试集，epochs次数为50，隐藏层神经元个数为12个。

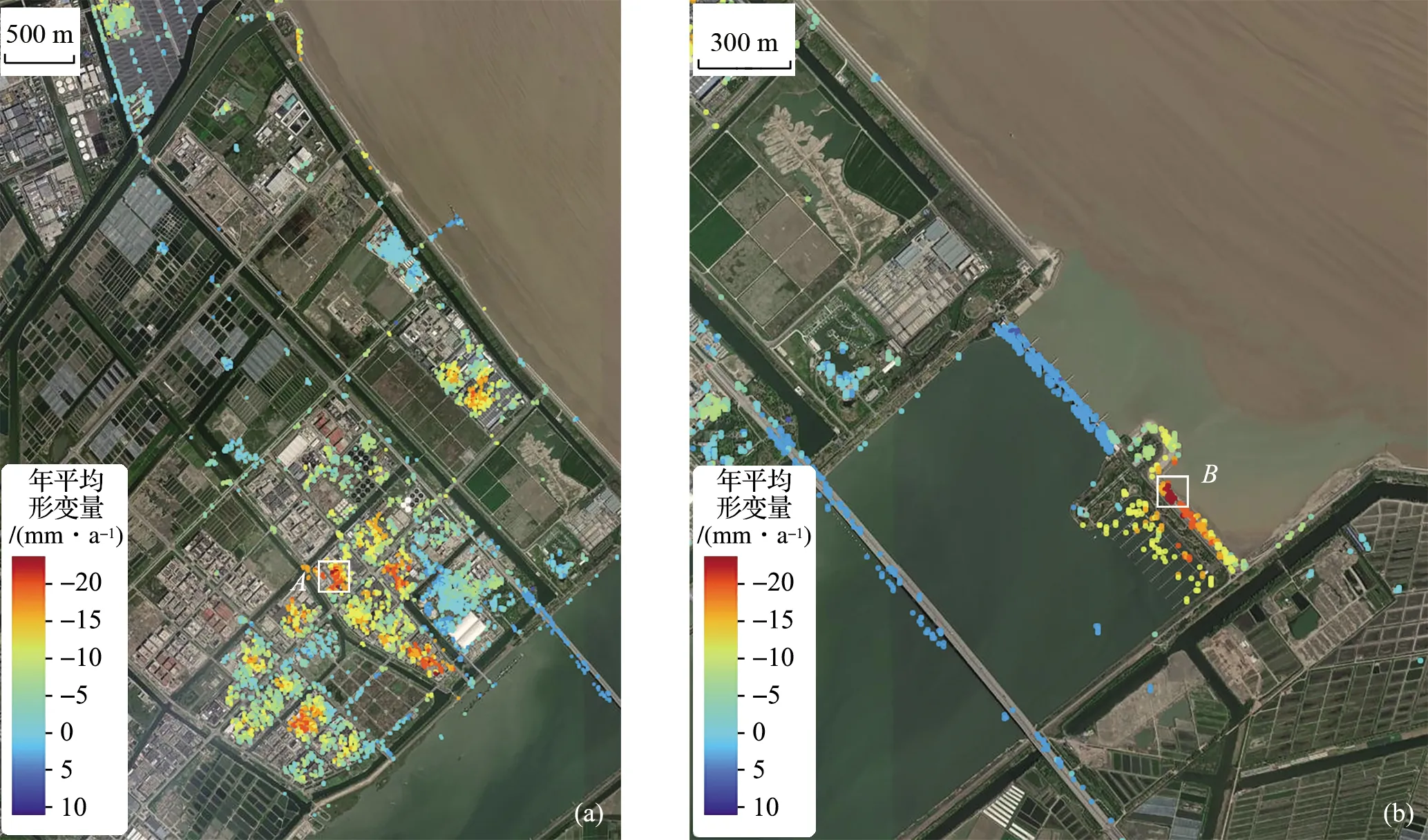
图6 选取的PS点A(a)和B(b)

图7为在A、B两点不同方法时序预测结果的对比，图8为在A、B两点不同方法相对误差结果的对比，其RMSE、MAE以及μ指标结果如表1所示。从图7中可以看到3种方法均会出现预测结果滞后的情况，这源自于对过去信息的一种记忆方式。在对t时刻的值进行预测的时候，预测值往往与t时刻的前几个时刻的值有一定关系，当信息数量很小的情况下，前一个时刻的实际值yt-1所对应的权重较大，因而其预测结果会更偏向于yt-1，反映在图中就会显示为预测结果滞后。从图8中可以更明显地看出3种方法在同一个测试集中的表现，图中展示了3种方法的预测相对误差按照由小到大的顺序排列而得到的结果。这里的相对误差指的是3种方法得到的时序值，分别与InSAR时间序列值作差的绝对值除以InSAR时间序列值的绝对值而得到的数值。其中，ARIMA和LSTM方法的相对误差大小比较接近，而ARIMA-LSTM方法的相对误差明显更小。

图7 3种预测方法时序预测结果对比

图8 3种预测方法的相对误差结果对比

表1 3种预测方法的精度指标对比

由表1的统计结果可知，本文提出的ARIMA-LSTM方法，相比于传统单一的ARIMA方法或者LSTM方法，预测精度明显提升。其中，RMSE至少减小了 2.23 mm，MAE至少减小了0.98 mm，μ至少提升了15.19%。

3 结论

本文建立了一种联合ARIMA和LSTM的地面沉降监测和预测方法，对InSAR形变量时间序列与ARIMA预测形变量时间序列之间的差值序列进行预测，与传统的单一LSTM或ARIMA模型预测相比，其预测精度有所提升，其中，RMSE至少减小了 2.23 mm，MAE至少减小了0.98 mm，μ至少提升了15.19%。

海陆过渡带地面沉降的监测和预测意义重大，其中地面沉降预测更是国内外的难点问题，通过本文的研究，不仅发现了杭州湾地区的严重沉降区域，并且使用ARIMA-LSTM方法对历史数据进行了计算分析，建立了一种新的预测模型，可为海陆过渡带地面沉降的预警提供技术借鉴。