事件触发机制下的多速率多智能体系统非脆弱一致性控制

刘建华，李佳慧，刘小斌，穆树娟，董宏丽

（1. 东北石油大学 人工智能能源研究院，黑龙江 大庆 163318；2. 上海电子信息职业技术学院 中德工程学院，上海 201411；3. 东北石油大学 黑龙江省网络化与智能控制重点实验室，黑龙江 大庆 163318；4. 东北石油大学三亚海洋油气研究院，海南 三亚 572024）

在过去的几十年里，多智能体系统由于在化学制造业、地质勘探、楼宇自动化以及航空航天等各个领域的广泛应用而吸引了大量学者的目光[1-4]。作为多智能体系统的主要研究课题之一，一致性控制问题持续受到关注[5-8]，其目标是通过利用邻居节点的信息设计一致性算法(或协议)，使多智能体的状态达到某些共同特征(如位置、相位、速度和姿态)，目前在该方面已经涌现了大批优秀成果。例如，文献[5]研究了拓扑结构变化的多智能体系统，考虑了在受到模型不确定性和外部扰动影响下的一致性控制问题。文献[7]对离散时间多智能体系统，同时考虑了外部干扰和测量丢失，并深入研究了测量丢失对一致性行为的影响。此外，为了提高通信可靠性，引入了冗余信道，并构建了相应的冗余信道信息传输协议。文献[8]使用相对输出测量的方法解决了具有一般线性节点的动态多智能体系统的分布式H∞一致性控制问题。

值得注意的是，现有的大多数控制器设计方法都依赖于一个假设，即所设计的控制器可以精确地实现。然而，由于复杂和多变的环境会对控制器执行过程造成一定程度的干扰[9-13]，导致这一假设在现实中并不总是成立的。为了解决这一问题，学者们设计了非脆弱控制器来容忍控制器增益中的扰动项。在文献[9]中，基于切换有向网络拓扑，提出了一种非脆弱控制方案，以确保具有时变输入时滞的线性连续时间多智能体系统实现有限时间一致性控制。文献[10]分别针对有时滞和无时滞的分数阶记忆(Bidirectional Associative Memory,BAM)神经网络，给出了分数阶BAM神经网络的非脆弱状态估计方法，引入了一种新的变换，将分数阶BAM神经网络转换为带有参数不确定的系统。文献[11]研究了连续时间广义多智能体系统在Lipschitz非线性动力学下的非脆弱一致性控制问题。考虑了相关的非线性多智能体在无向图中通信的情况，最终所有智能体的状态通过所设计控制协议达成一致。更多相关结果见文献[12-16]。

在复杂的实际系统中，不同的信号往往根据其物理特性采用不同的采样率进行采样，也就是说更多的工程系统实际上是多速率系统[17-21]。例如,在机器人和制造业系统中，测量是通过图像处理来进行视觉反馈，它们都需要较长的时间才能实现采样，这就导致了大的采样周期。因此，对于不同的元件采用不同的采样率(即多速率采样)能够使系统性能和资源消耗达到一个恰当的平衡状态，所以研究多速率系统具有很好的理论意义和工业价值。由于多速率采样带来的复杂性，关于多速率系统的分析与综合已经受到了广泛关注，如稳定性分析、H∞一致性控制、模型预测控制及故障检测[22-36]。文献[24]讨论了一类时变时滞网络化控制系统的镇定问题，其中随机时滞小于一个传感器周期或大于一个传感器周期但有界。文中提出了一种新的多速率方法来建立短随机时滞和长随机时滞的联合模型。文献[28]针对带有随机噪声、未知输入以及执行器和传感器故障的系统，解决了多速率多传感器融合系统的故障检测问题和最优滤波问题。值得指出的是，虽然多速率采样问题已经被大量研究，但在多智能体系统中少有考虑。因此，本文的第一个研究动机是探索多速率采样对多智能体系统非脆弱一致性控制问题的影响。

众所周知，在恶劣的环境下智能体的通信资源和运算能力通常是被限制的[37-38]，为了降低资源的损耗，基于事件触发的通信方式进入了人们的视野[39-44]。瑞典学者Åarzén于20世纪90年代末第一次提出了基于事件触发机制的PID控制策略[45]，并对事件触发机制进行了详细的分析。与时间触发机制不同，事件触发机制的核心思想是“按需”触发，而不再是“按时”触发。根据实际需求预先设定触发条件，只有系统的当前信息满足触发条件，才执行当前触发任务。显而易见，事件触发机制的应用会降低资源的消耗。在文献[39]中，作者清楚地描述了时间触发和事件触发的区别，并阐述了事件触发在节约通信资源方面的优势。值得注意的是，目前基于事件触发机制的多智能体系统一致性控制问题的研究大多数聚焦于单速率采样，本文将研究事件触发机制对多速率多智能体系统一致性控制问题的影响，并提出相应的一致性控制方案。

基于以上讨论，本文将针对多速率多智能体系统，研究其在事件触发机制下的非脆弱H∞一致性控制问题。具体贡献如下：(1) 首次研究了一类多速率多智能体系统的非脆弱H∞一致性控制问题；(2) 与时间触发机制相比，引入的事件触发机制在节约通信资源方面更具优势并且采用了相对触发的形式来动态调整阈值，使系统的性能和资源的消耗达到恰当的平衡；(3) 获得了增广系统渐近稳定且满足给定H∞一致性控制约束的充分条件。

1 预备知识

1.1 图论

1.2 引理

2 问题描述

2.1 模型描述

首先，考虑由以下状态空间模型描述的多智能体系统

式中：

2.2 控制器设计

2.3 系统增广

为方便以下分析，先做出如下定义：

由以上结果可知，式(10)中的事件触发条件为

3 主要结果

3.1 一致性控制分析

3.2 增益求解

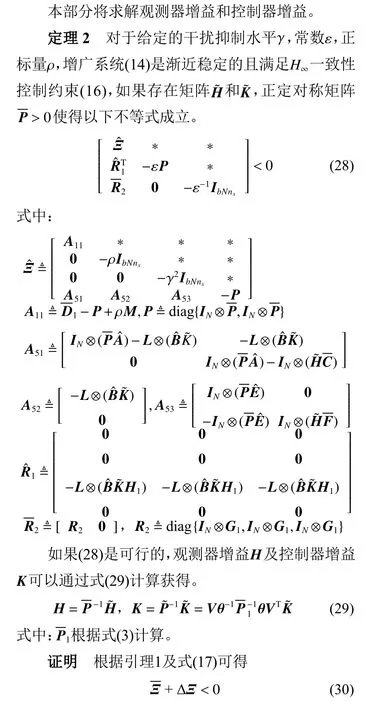
式中：

4 仿真结果

本节将提供一个数值仿真例子来验证所提出控制方法的有效性。

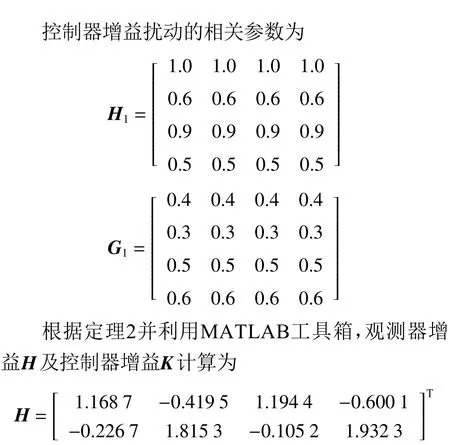
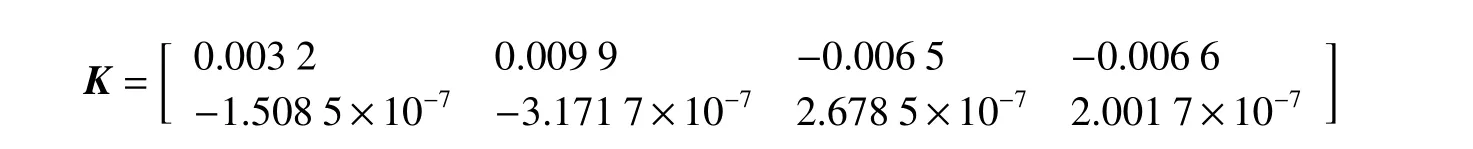
仿真结果见图2～10。图2～3绘制了在非脆弱控制器控制下3个智能体的状态轨迹，其中xiς(Tm)表 示第i智能体的第ς 个 状态( ς=1,2)，从图中可以看出，随着时间的推移，状态最终趋于一致。图4～5绘制了在具有一般形式的控制器下3个智能体的状态轨迹。很明显，本文所提出的控制方法更加有效，体现了所提出控制方法的优越性。图6～7绘制了智能体i的测量输出，从图中可以看出采样时刻为0，2， 4，···，60，测量输出的采样数只有状态的一半，降低了采样成本，体现了多速率策略的优势。图8～9展示了一致性误差z(k)−ℓz(k)，随着时间推移，误差趋于0。此外，图10描绘了3个智能体的触发时刻，显然信息传输的次数和控制协议的更新次数明显减少，有效缓解了通信负担。

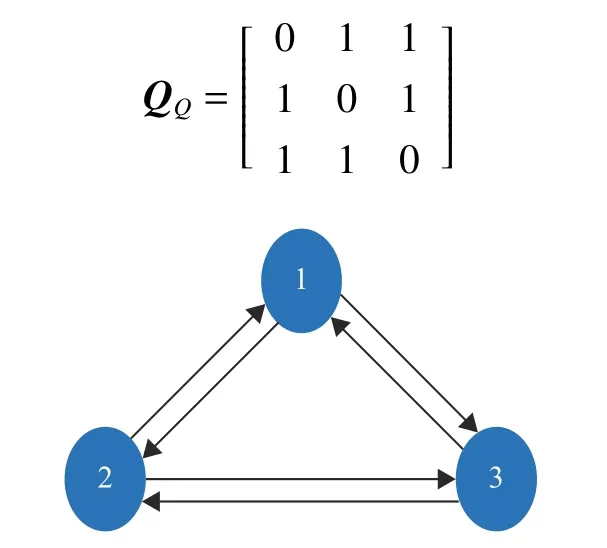
图1 拓扑结构Fig.1 Topology

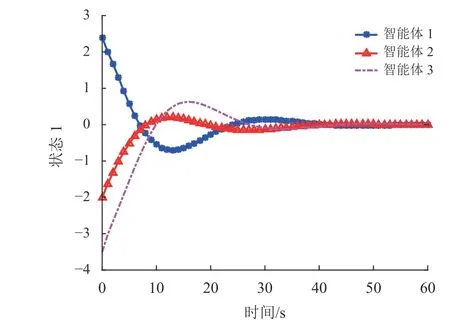
图2 非脆弱控制器下3个智能体的状态轨迹xi1(Tm)Fig.2 The state trajectories xi1(Tm) of the three agents under the non-fragile controller

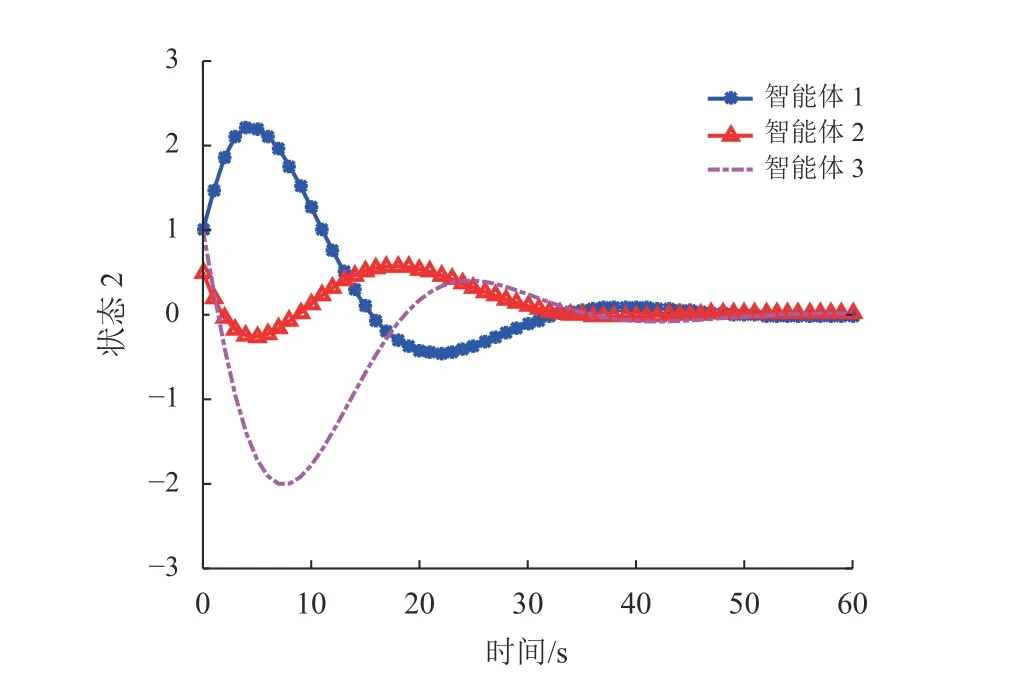
图3 非脆弱控制器下3个智能体的状态轨迹xi2(Tm)Fig.3 The state trajectories x i2(Tm) of the three agents under the non-fragile controller

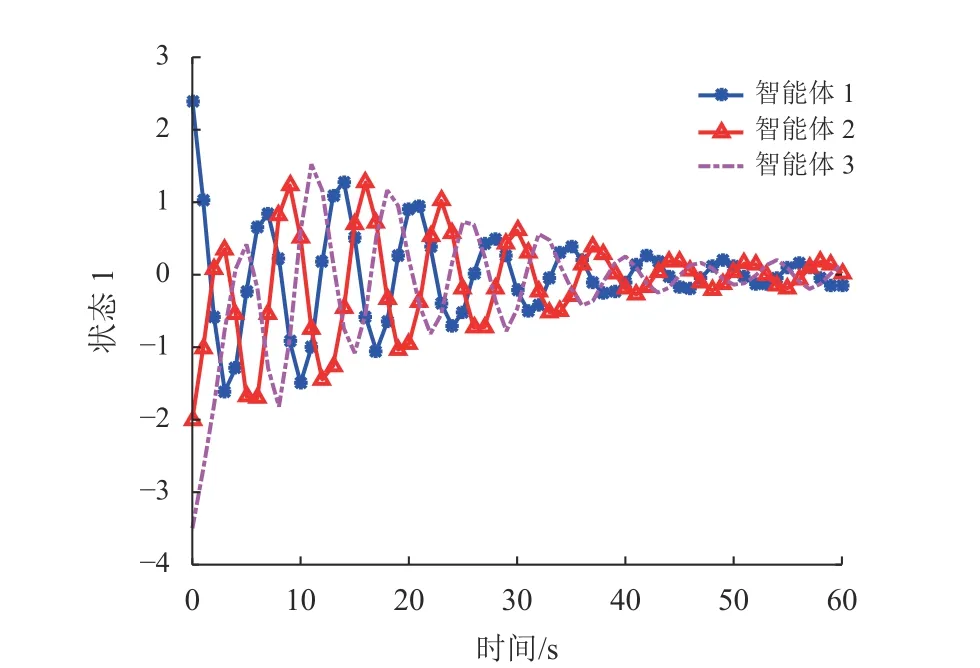
图4 一般控制器下3个智能体的状态轨迹xi1(Tm)Fig.4 The state trajectories x i1(Tm) of the three agents under the general controller

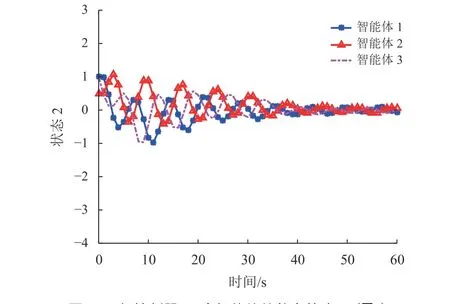
图5 一般控制器下3个智能体的状态轨迹xi2(Tm)Fig.5 The state trajectoriesxi2(Tm)of thethree agentsunder the general controller

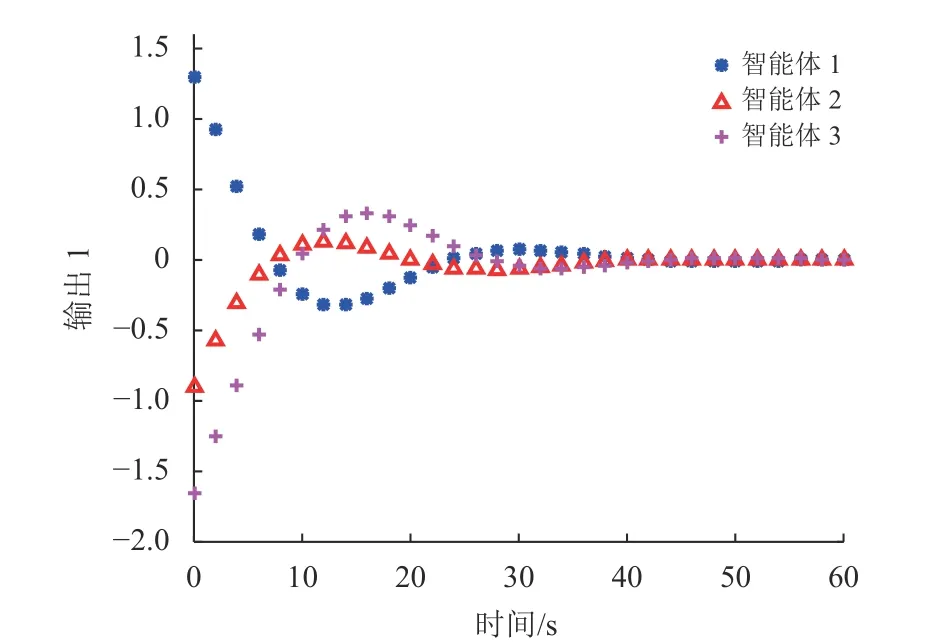
图6 3个智能体的测量输出yi1(tm)Fig.6 Measurement outputs y i1(tm) of the three agents

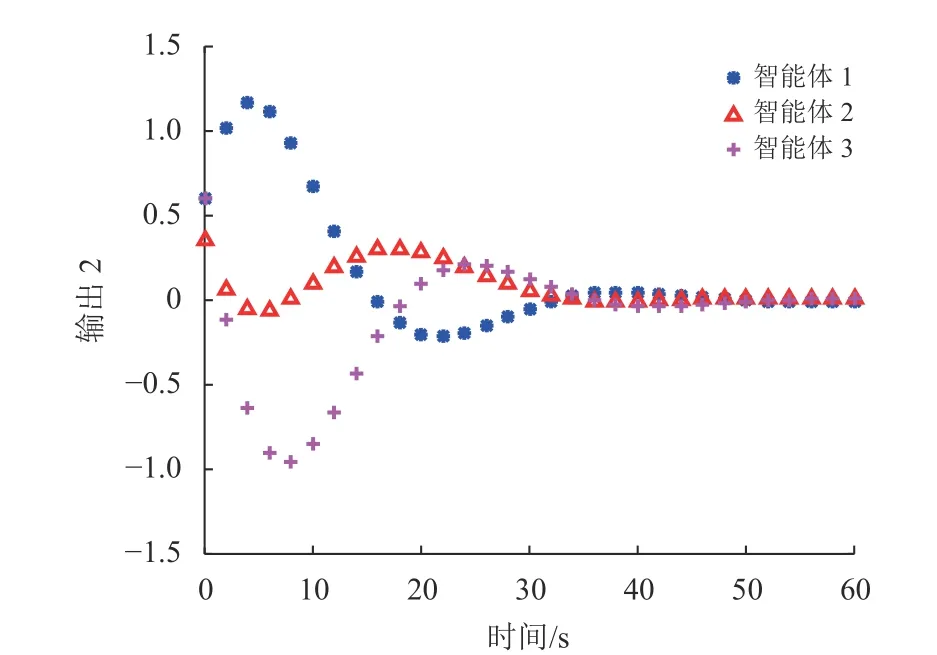
图7 3个智能体的测量输出yi2(tm)Fig.7 Measurement outputsy i2(tm)ofthe three agents

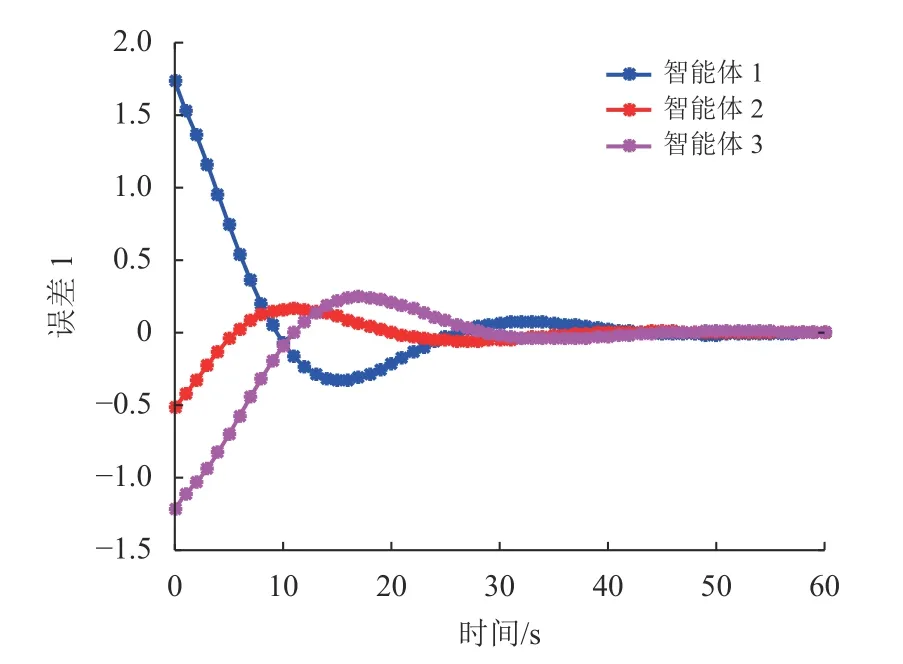
图8 一致性误差1Fig.8 Consensus error 1

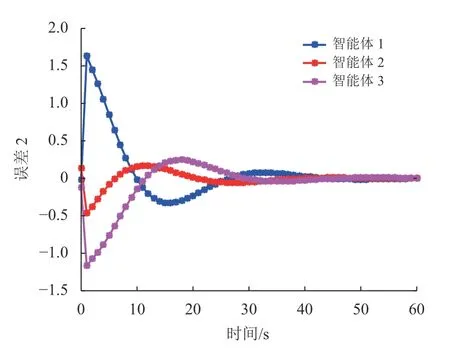
图9 一致性误差2Fig.9 Consensus error 2

图10 3个智能体的触发时刻Fig.10 Triggering instants of three agents

5 结论

本文针对一类多速率多智能体系统，研究了在事件触发机制下的非脆弱H∞一致性控制问题。首先，利用提升技术将多速率多智能体系统统一为单速率多智能体系统。接下来，对比时间触发机制，提出了一种基于相对事件触发机制的分布式一致性控制方案，并且所设计的控制器具有非脆弱性。然后，利用Lyapunov稳定性理论，获得了增广系统渐近稳定且满足给定H∞一致性控制约束的充分条件。最后，通过数值例子验证了所提出控制方案的有效性。论文未来潜在的研究方向总结如下：(1) 提升技术的使用造成了大量计算负担，寻找更有效的方法来处理多速率系统；(2) 将研究结果扩展到更复杂的系统，如时滞系统、马尔可夫跳变系统、T-S模糊系统和传感器网络；(3) 研究信道衰落、编码解码机制等对多智能体系统一致性控制问题的影响。