就近原则下新增应急避难点的鲁棒选址策略研究
李红梅 邓 洁 罗太波 齐捧虎
(1.西北大学 经济管理学院,陕西 西安 710127;2.西安电子科技大学 经济与管理学院,陕西 西安 710126)
0 引言
回顾过去的近二十年,各类自然灾害、事故灾难、公共卫生事件以及社会安全事件在全球各个国家和地区频繁发生,给世界各国人民的生命和财产安全、公共安全以及社会秩序等带来了不同程度的影响。健全的城市应急管理系统能有效地降低甚至预防突发事件带来的巨大损失,而应急避难点选址是应急管理中极为重要的一部分,合理的应急避难点选址可以高效的完成紧急情况下疏散任务,降低突发事件的危害,同时预防二次灾难的发生。已有的应急避难点多是根据当时城市的规模和需求建设的,然而随着我国城市的快速发展,城市规模不断扩大,城市人口数量剧增,已有的应急避难点已经不能满足城市发展的需求。如何在已有避难点的基础上规划新增应急避难点,成为了许多城市亟须解决的问题。灾害自身的不确定性导致在规划应急避难点时很难对潜在疏散点的疏散人数进行准确的估算,大部分情况只能给出区间估计;与此同时,由于紧急避难时大量人口瞬间涌入道路,难免导致疏散过程中出现堵塞等情况,这些问题都增加了新增应急避难点选址的难度。本文考虑在城市的不断发展变化导致原有避难点系统无法应对当前情况下,研究如何对新增应急避难点进行选址以达到一定的优化目标。考虑到疏散点人数的不确定性,结合应急避难疏散的特殊需求,为更加贴近现实疏散目标,本文采用最小最大后悔准则作为选址方案的评价准则,以此保障即使在最坏的情况下选址方案也有可接受的表现。
国际上最早的应急避难设施选址问题是Toregas 等[1]在1971 年提出的,他们研究如何建立数量最少的应急救援点,以便在规定时间内能够给所有需要应急服务的需求点提供救援,即为后来的集合覆盖问题(set covering problem)。早期的应急避难点选址模型主要包括了覆盖模型(covering problem)、中心点模型(center problem)和中值点模型(median problem)。关于覆盖问题的相关研究可以参考综述性文献[2];有关中心点和中值点问题的研究可以参考综述性文献[3-4]。对于新增设施的选址问题,最早的研究是基于中心点选址问题而来,称为有条件的选址问题[5-6](conditional location problem)。他们首先研究了在网络中已有q(q≥1)个设施的情况下,如何新建p=1 个设施以使得目标函数最优。Chen 和Handler[7]考虑平面上有条件的p-中心点选址问题(p≥1) 并给出了一种逐次逼近算法用以求解。Chen[8]在前面研究的基础上进一步考虑了平面上有条件的p-中心点选址问题和中值点选址问题并给出了求解思路。之后Chen 和Handler[9]提出了另一种算法用以解决平面上有条件的p-中心点选址问题。Drezner[10]则提出通过解决O(logn) 个传统的中心点选址问题求解有条件的p-中心点选址问题的算法。后来Drezner[11]又提出了求解有条件的p-中值点选址问题的启发式算法。值得一提的是文献[10-11]中的方法同时适用于平面和网络两种情况。Berman 和Simchi-Levi[12]将网络上的有条件的p-中心点/中值点选址问题转换为求解传统的(p+1)-中心点/中值点选址问题。Berman 和Drezner[13]提出了另一种简洁的求解方法,通过建立合适的最短路矩阵将网络上有条件的p-中心点/中值点选址问题转换为传统的p-中心点/中值点问题求解。Chen和Chen[14]在文献[7]的基础上提出了一种新的逐次逼近算法求解有条件的p-中心点选址问题。
本文研究一般网络图上已有若干个应急避难点时新增一个应急避难点的选址问题。但与以往研究不同,考虑到突发事件的不确定性,疏散网络中各顶点的权重通常难以确定,但其所属区间范围一般可以知道,因此本文研究的疏散网络中顶点权重以区间数据的形式给定。同时,考虑到应急环境下大量人流短时间迅速转移易形成局部堵塞,本文对疏散网络中的道路引入容量参数,以此表示路段的通行能力。同时关于考虑疏散人数不确定和疏散中堵塞时间成本的选址问题也有相关研究,称为sink 选址问题。Sink 选址问题最初由Cheng 等[15]提出,他们考虑在一条具有个n顶点的路上选择1 个点作为应急避难点的1-sink 选址问题,并给出了时间复杂度为O(nlog2n) 的算法,之后有多个改进的算法[16][17],目前最优的算法时间复杂度为O(n)[18];文献[18]中同时将求解一条路上2 个sink 的选址问题的时间复杂度由O(n3logn)[19]改进到了O(nlog4n);对于一条路上k个sink 的选址问题也有学者进行了研究并给出了求解算法[20][21]。针对树上1 个sink 的选址问题,Higashikawa 等[22]给出了时间复杂度为O(n2log2n) 的算法,Bhattacharya 和Kameda[18]进一步设计了时间复杂度为O(nlogn) 的算法;Golin 和Sandeep[23]设计了求解树上k 个sink 选址问题的算法,时间复杂度为O(max(k2,log2n)k2n2log5n)。Xu 和Li[24]针对圈上1 个sink 选址问题给出了时间复杂度为O(n3logn)的算法,Benkoczi 等[25]给出了时间复杂度为O(n2) 的算法。一般网络图上的sink 选址问题研究成果有限,Li 和Xu[26]假设所有人就近避难,考虑1 个sink 的选址,给出了时间复杂度为O(m2n3) 求解算法。以上相关研究的优化目标都是最大完成时间的最大后悔值最小,也有学者考虑以总完成时间的最大后悔值最小为目标,针对路上1 个sink 的选址问题给出了相应的求解算法[27-28]。需要说明的是,在以上最小最大后悔sink 选址问题研究中,均包含了以下假设:(1)疏散网络中所有的边都具有相同的容量;(2)应急避难点入口为无限大,权重到达即完成避难,不考虑进入时间,因此若一个应急避难点建立在某个顶点上,该顶点上的权重可视为在瞬间完成避难。(3)同一个顶点上的权重应当经由相同的疏散路径到达同一个应急避难点;(4)疏散过程中不允许出现权重对流。在讨论本文研究问题的过程中,将沿用这些假设。
本文在已有研究的基础上,考虑疏散人数的不确定性和疏散过程中人流堵塞带来的时间成本,假设在一般图G=(V,E) 中上已存在k-1(k≥2) 个应急避难点,对如何新增一个(第k个)应急避难点的选址问题展开研究。鉴于在灾难发生时,群众习惯去往距离自己最近的避难点进行避难[26],因此本文假设所有权重均以就近避难作为选择避难点和避难路径的原则。同时,与之前的相关研究一样,假设疏散网络中所有的边都具有相同的容量。目标函数的设定以最大完成时间(所有权重到达避难点的时间)为基础,采用鲁棒优化的思想,以最坏场景为目标,寻求使得最大完成时间的最大后悔值最小的新增避难点选址方案。
1 问题定义与性质分析
1.1 问题定义
在一般网络连通图G=(V,E) 上,顶点集V=(v1,v2,…,vn) 表示网络中避难者的分布点,边集E表示网络中的道路集合,且| E|=m。对于边e∈E,l(e) 为该道路的长度,且每条道路具有相同的通行能力c,也即单位时间能够进入道路的最大权重数。对于任意顶点vi∈V,该顶点需要避难的人数在灾害发生前是不确定的,仅知道人数区间为,且;在灾害发生时,该顶点需要避难的人数从客观上是确定值。假设某顶点vi上有wi单位的权重要进入边e,由于道路通行能力c <wi,那么顶点vi上的部分权重需要等待一定的时间才能进入道路,即产生堵塞。令场景集合S表示所有可能的权重wi的笛卡尔积(1 ≤i≤n)。当场景s∈S给定时,wi(s) 表示该场景下顶点vi的权重。定义τ为单位权重在各路段上移动单位距离所需的时间。G中任意两点x和y的最短距离为d(x,y),且恒有d(x,y)=d(y,x)。本文假设图中任意两点间的最短路径和路径长度已知。由于G是连通图,即m≥n-1,但是当m=n-1 时,一般图G成为树图,因此,假设m≥n。
不失一般性,假设图G中已有k-1 个避难点,其在网络图中对应的位置分别记为x1,x2,…,xk-1。图中每个顶点的避难者根据最短路径选择距离最近的避难点避难(若一个顶点与多个避难点间的最短路径距离相同,则选择排序靠前的避难点;若一个顶点与一个避难点间有多条距离相同的最短路径,则选择最靠右的路径)。在实际中,为了不出现混乱,假设各顶点的权重在向避难点撤离时视为一个整体且不允许出现交叉流。现在需要在现有避难点的基础上再增加一个避难点,假设其选择的位置为xk。对于vi,x(vi) 表示顶点vi在原有k-1 个避难点中选择的避难点位置。如果d(vi,xk)≥d(vi,x(vi)),则该顶点选择的避难点位置保持不变;如果d(vi,xk)<d(vi,x(vi)),则该顶点选择的避难点位置变为xk。记X(xk)={x1,x2,…,xk-1,xk} 表示第k个避难点选址在xk时,所有避难点位置的集合。在场景s下,定义F(X(xk),s)为第k个避难点选址在xk处时,所有权重完成撤离的时间。用xopt(s) 表示场景s下第k个避难点的最优选址位置(面对场景s,在该选址方案下,所有权重完成撤离的时间最小),则X(xopt(s))表示第k个应急避难点选在最优位置xopt(s) 时的所有避难点集合,即X(xopt(s))={x1,x2,…,xk-1,xopt(s)},相应的,F(X(xopt(s)),s)为场景s下,该选址方案下图G中所有权重完成撤离的时间。在场景s下,应急避难点选在xk处的后悔值定义为:

应急避难点选在xk处的最大后悔值定义为Rmax(X(xk))=。场景称为应急避难点选在xk处的最坏场景,即。该问题的目标是找到第k个避难点的最优选址,使得其最大后悔值Rmax(X(xk)) 达到最小,即

1.2 性质分析
通过对图和路径的分析,基于不同的选址位置,先把一般网络图分解成多项式个树图,而后分析最坏场景的结构,找到所有的可能最坏场景。
当新的应急避难点选在某一点xk时,图G中的每个顶点将根据就近原则选择自身要到达的避难点并确定对应的到达路径。此时,可以把图G分解为k个以x1,x2,…,xk-1,xk为根节点的相互独立的树,不妨记为T(x1),T(x2),…,T(xk-1),T(xk)。注意这里的k个树一定是相互独立的;否则不妨假设某两个树图T(xi) 和T(xj)(i,j∈[1,k],i≠j) 存在公共顶点vl,但是vl根据就近原则选择避难点时,必然选择唯一的一个避难点和到达路径,这与假设相矛盾,因此,由图G分解而成的k个树图一定相互独立。以图1为例,图G中有三个避难点,首先,图中各顶点根据就近原则选择自身要到达的避难点,假设选择x1的顶点有{v1,v2,v3},选择x2的顶点有{v4,v5},选择x3的顶点有{v6}。然后,把图G分解为分别以三个避难点为根节点的相互独立的树图。

图1 一般网络图到树的转换示意图Figure 1 Illustration of a general network to tree networks with given sinks
记F(xi,s)表示场景s下,树T(xi)中所有权重完成撤离的时间(1 ≤i≤k),那么有
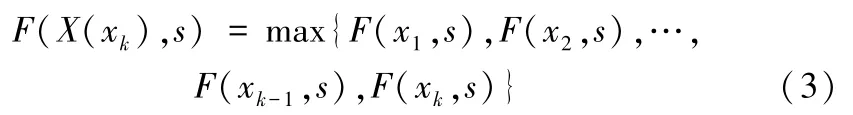
下面介绍F(xi,s)(1≤i≤k)的计算过程,不妨以F(xk,s)为例。对于任意xk∈G,记δ(xk)={中e=(xk,vi)存在},表示树T(xk)中所有与xk相邻的顶点集合。对于任意vi∈T(xk),vi的撤离路径一定经过顶点vj∈δ(xk)。T(xk)中以vi为根的子树记为T(xk,vi),相应的,表示场景s下,T(xk,vi)中所有权重完成撤离的时间。因此,在场景s下有
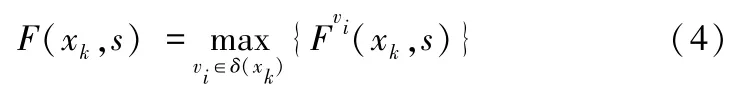
假设T(xk,vi) 中有n′个顶点,记为u1,u2,…,un′(=vi),且d(xk,ui) ≤d(xk,ui-1),2 ≤i≤n′。Kamiyama 等[29]已经证明了在d(xk,ui) 保持不变,且道路通行能力相同时,如果将xk和ui(1≤i≤n′)移至一条直线上,那么保持不变(如图2 所示)。因此有

图2 树到路的转换示意图Figure 2 Illustration of a tree network to a path network
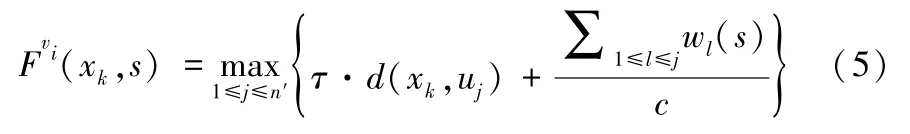
注意本文假设避难点的容量是无限大的,并且如果避难点位于顶点处,则该顶点的所有权重完成撤离的时间为零。
在给定场景s下,考虑当xk位于边e=(vp,vq) 上时,对于任意vi∈V到达避难点的最短路径有三种可能:(1)vi选择的避难点为x(vi)(vi在原有k-1 个避难点中选择的避难点位置),记做路径P1;(2)vi选择的避难点为xk,且经过vp到达,记做路径P2;(3)vi选择的避难点为xk,且经过vq到达,记做路径P3。为了后面分析的需要,引入敏感点的概念。
定义1边e=(vp,vq) 上,当xk∈(vp,x′]和xk∈(x′,vq)时,如果至少存在一个顶点vi∈V使得vi选择的撤离路径不同,则称x′为边e上的一个敏感点。
令gi=| d(vi,vp)-d(vi,vq)|,hi=d(vi,x(vi))-d(vi,vp)。接下来,将根据避难点xk在边e=(vp,vq) 上的不同选址情况,对边上的敏感点进行详细分析。
情形1若gi=0,分三种子情形讨论。
(1)如果hi≤0,那么边e上没有敏感点;
(2)如果0<hi≤,当xk∈(vp,vp +hi)时,vi选择P2;当xk∈[vp+hi,vq -hi]时,vi选择P1;当xk∈(vq -hi,vq) 时,vi选择P3;
(3)如果hi>,当xk∈时,vi选择P2;当xk∈时,vi选择P3。
即在情形1 下,vp +hi、vq -hi、vp +为边e上的敏感点。
情形2若0<gi≤d(vp,vq),分两种子情形进行讨论。
(1)当d(vi,vp)<d(vi,vq) 时,①如果hi≤0 且hi -gi≤0,那么边e上没有敏感点;②如果hi>0 且hi -gi≤0,当xk∈(vp,vp +hi)时,vi选择P2;当xk∈[vp +hi,vq)时,vi选择P1。③如果0<hi≤且0<hi -gi≤,当xk∈(vp,vp +hi) 时,vi选择P2;当xk∈[vp +hi,vq -hi +gi]时,vi选择P1;当xk∈(vq -hi +gi,vq)时,vi选择P3。④如果hi>,当xk∈时,vi选择P2;当xk∈时,vi选择P3。
(2)当d(vi,vp)>d(vi,vq) 时,①如果hi +gi≤0,那么边e上没有敏感点。②如果hi +gi>0且hi≤0,当xk∈(vp,vq -hi -gi]时,vi选择P1;当xk∈(vq -hi -gi,vq) 时,vi选择P3。③如果0<hi+gi≤且0<hi≤,当xk∈(vp,vp+hi) 时,vi选择P2;当xk∈[vp+hi,vq -hi -gi]时,vi选择P1;当xk∈(vq -hi -gi,vq) 时,vi选择P3。④如果hi>,当xk∈时,vi选择P2;
当xk∈时,vi选择P3。
即在情形2 下,vp +hi、vq -hi +gi、vp +、vq-hi -gi、vp +为边e上的敏感点。
情形3若gi >d(vp,vq),同样分下面两种子情形进行讨论。
(1)当d(vi,vp)<d(vi,vq) 时,①如果hi≤0,那么边e上没有敏感点。②如果0<hi≤d(vp,vq),当xk∈(vp,vp +hi) 时,vi选择P2;当xk∈[vp+hi,vq) 时,vi选择P1。③如果d(vp,vq)<hi,那么边e上没有敏感点。
(2)当d(vi,vp)>d(vi,vq) 时,①如果hi +gi≤0,那么边e上没有敏感点。②如果0<hi +gi≤d(vp,vq),当xk∈(vp,vq -hi -gi]时,vi选择P1;当xk∈(vq -hi -gi,vq) 时,vi选择P3。③如果d(vp,vq)<hi+gi,那么边e上没有敏感点。
即在情形3 下,vp+hi、vq -hi -gi为边e上的敏感点。
通过以上对敏感点的分析,可以得到下面的引理。
引理1若选定一条边e,e上所有敏感点构成集合Ce,那么Ce包含O(n) 个元素,且计算出Ce的时间复杂度为O(n)。
完成对敏感点的分析后,接下来分析最坏场景的结构特征。在给定场景s下,若应急避难点选在xk处,假设G中所有权重完成撤离的时间由T(xk) 中所有权重完成撤离的时间决定,而T(xk) 中所有权重完成撤离的时间由子树T(xk,vi)中所有权重完成撤离的时间决定,即

根据已有研究的结果[22-23],树上的sink 选址问题转换为路上的sink 选址问题后,最坏场景的结构特征能够保留。定义可能最坏场景如下:
定义2给定第k个避难点的选址xk后,考虑任意一棵子树T(xj,vi),其中1 ≤j≤k,vi∈δ(xj),假设该子树中有n′个顶点,记为u1,u2,…,un′(=vi),且d(xj,ui) ≤d(xj,ui-1),2 ≤i≤n′。如果场景s(xk) 满足对于顶点ul(1 ≤l≤n′),有wf(s(xk))=,且wf(s(xk))=,对于所有的顶点vg∉T(xj,vi),有wg(s(xk))=,则称s(xk) 为避难点选在xk时的一个可能最坏场景。
根据定义可知,选定一个xk后就有一系列关于xk的可能最坏场景,记xk的所有可能最坏场景组成的集合为D(xk),D(xk) 包含O(n) 个元素[22]。
引理2若避难点选在xk处,那么对于任意s∈S,存在一个可能最坏场景s(xk)∈D(xk),使得R(X(xk),s(xk))≥R(X(xk),s)。
引理2 是显然成立的,这里不再给出证明。由引理2 可知,对于任意xk∈G,避难点选在xk处的最坏场景一定在D(xk) 中。记D=表示避难点xk选在G中任意位置时所有可能最坏场景组成的集合。接下来,将对D的结构进行详细分析。

引理3D包含O(mn2) 个场景。
证明:由于G有n个顶点,m条边,给定一条边e,Ce包含O(n)个元素,且给定xk后,D(xk)包含O(n)个场景,所以,D包含O(mn2) 个场景。


图3 xk∈e=(vp,vq)时的示意图Figure 3 Illustration of where xk∈e=(vp,vq)


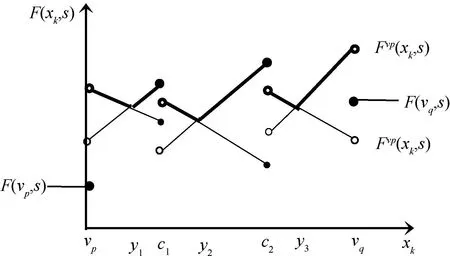
图4 xk∈e=(vp,vq)时的F(xk,s)及y1,y2,y3 示意图Figure 4 Illustration of F(xk,s) and y1,y2,y3 where xk∈e=(vp,vq)

引理5给定一条边e和一个场景s,Ye包含O(n) 个元素。

2 算法设计
2.1 最优避难点选址
根据引理4,给定任意一个场景s,最优避难点选址为:
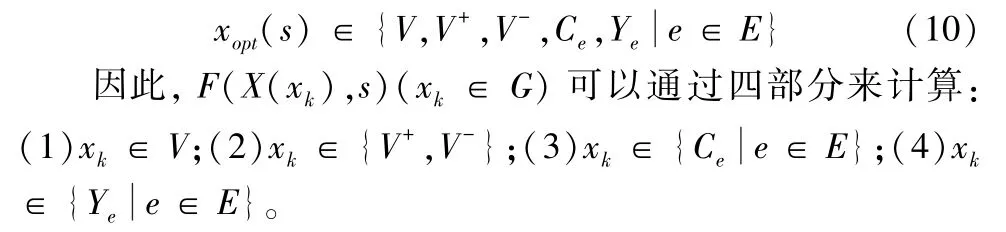
引理6给定一个场景s,当避难点选定在xk时,得到F(X(xk),s) 的时间复杂度为O(n)。
证明:场景s下,若避难点选定在xk。首先,所有顶点选择自身到达的避难点后,图G将分解为k个树图T(x1),T(x2),…,T(xk-1),T(xk),其时间复杂度为O(n),记子树T(xi)中的顶点数为ni(1≤i≤k)。下面,以T(xk)中所有权重完成撤离的时间F(xk,s) 为例(其余树中所有权重完成撤离的时间同理可得),有

结合上一节的性质分析和引理6,给定一个确定的场景s,求解最大完成时间最小的选址方案(即最优选址方案) 的算法如表1 所示,易知该算法的时间复杂度为O(mn2)。针对确定场景下求解最优选址方案的问题,本小节给出下面的定理。

表1 确定场景下最优选址方案求解算法Table 1 The optimal sink location algorithm
定理1给定一个场景s,一般网络图中,就近原则下新增应急避难点的最优选址问题可在O(mn2) 时间求解。
2.2 最小最大后悔避难点选址
由引理3 可知,D包含O(mn2) 个场景。避难点xk在理论上有无穷多种选址方案,但当xk落在特定范围内时(范围分界点包括顶点和敏感点),疏散网络对应的树图是保持不变的。因此,根据xk的不同取值,可以将D分为O(mn)组场景,每组场景包含O(n) 个元素,即D(xk)。
引理7若避难点选定在xk且给定场景D(xk),那么对所有s∈D(xk),F(X(xk),s) 可以通过O(n2) 时间得到。
证明:给定xk,D(xk) 中包含O(n) 个场景。结合引理6可得上面的结论。
引理8对于所有xk∈V和所有s∈D(xk),得到F(X(xk),s) 的时间为O(n3)。
证明:由于图G中有n个顶点,每个顶点对应的可能最坏场景D(xk) 包含有O(n) 个元素,结合引理6 得证。
引理9对于所有xk∈{V+,V-}和所有s∈D(xk),得到F(X(xk),s) 的时间为O(mn2)。
证明:由于这里的虚拟顶点与边相关联,共需考虑2m个虚拟顶点。针对每个虚拟顶点需要考虑O(n) 个场景,结合引理6 可证。
引理10在给定边e上,对于所有xk∈Ce和所有s∈D(xk),得到F(X(xk),s) 的时间为O(n3)。
证明:由于给定边e后,Ce包含O(n) 个元素,且每个敏感点需考虑O(n) 个场景,结合引理6 可证。

引理12若给定边e=(vp,vq),针对所有s∈D,Ye以及对于所有yi∈Ye的F(X(yi),s) 通过O(mn4) 时间得到。

通过上述引理,可以得到:(1)对于所有xk∈V和所有s∈D(xk),得到F(X(xk),s) 的时间为O(n3)(引理8);(2)对于所有xk∈{V+,V-}和所有s∈D(xk),得到F(X(xk),s)的时间为O(mn2)(引理9);(3) 基于引理10,由于G中有m条边,因此,对于所有xk∈和所有s∈D(xk),F(X(xk),s) 通过O(mn3) 时间可得;(4) 基于引理12,对所有s∈D和所有e∈E,Ye及其对应的F(X(yi),s) 通过O(m2n4) 时间可得。
对于任意s,X(xopt(s))=和F(X(xopt(s)),s)通过O(mn2)时间可得(算法见表1)。由于需要考虑O(mn2)个场景,因此,对于所有s∈D,X(xopt(s))和F(X(xopt(s)),s)可以通过O(m2n4)时间得到,即引理13。
引理13对于所有s∈D,X(xopt(s)) 和F(X(xopt(s)),s) 通过O(m2n4) 时间可得。
接下来考虑如何求得最大后悔值最小的选址方案。可能的最坏场景的结构已经明确,计算得到任意点在所有可能最坏场景的后悔值,通过比较即可找到其对应的最大后悔值,最后给出对应最大后悔值最小的点。由于网络图G中有无穷多备选点,将其分为两部分进行讨论分析:(1)避难点xk位于顶点时,计算每个顶点处的最大后悔值,找到最大后悔值最小的选址点;(2)避难点xk位于边上时,把每条边分为O(n) 个区间,采用线性规划的方法计算每个区间中对应最大后悔值最小的点,进而通过比较找到每条边上对应最大后悔值最小的选址点。最后,比较两部分得到整体的最小最大后悔值选址点。
首先,考虑xk选在顶点处的情形。根据前面的分析(引理8、定理1) 可知,在O(n3) 时间可以得到F(X(xk),s)(对于所有xk∈V和所有s∈D(xk)),在O(mn4)时间可以得到F(X(xopt(s)),s)(对于所有s∈)。若xk选在vi∈V,对于所有s∈D(vi),R(X(vi),s) 通过O(n) 时间可得,Rmax(X(vi))=通 过O(n) 时 间 可得。因此,对于所有的vi∈V,Rmax(X(vi)) 通过O(n2) 时间可得。如果对于任意vi∈V,有Rmax(X(v*)) ≤Rmax(X(vi)),则X(v*) 为xk选在顶点时最大后悔值最小的避难点集。因此,可得引理14。
引理14X(v*) 和Rmax(X(v*)) 可通过O(mn4) 时间得到。
接下来,需要考虑xk选在边e=(vp,vq) 上的情形。由敏感点的定义可以将边e=(vp,vq) 分为O(n) 个区间,而且对于所有xk∈(ci,ci+1](0 ≤i≤t),D(xk) 是一样的。所以当xk∈(ci,ci+1]时,要得到Rmax(X(xk))只需考虑D(xk)中的O(n) 个场景,记为{s1,s2,…,sn}。例如,图G中原有一个避难点x1,现在增加一个避难点x2,且x2选在边e=(vp,vq)上时,在场景s下,令R(xi,s)=F(xi,s)-F(X(xopt(s)),s)(i=1,2),则R(X(x2),s)=max{R(x1,s),R(x2,s)}。当x2∈(ci,ci+1]时,在场景s下,R(x1,s)为定值,R(x2,s)为分段线性函数。那么x2∈(ci,ci+1]时,Rmax(X(x2)) 的结构如图5 所示,图中不同线型代表不同场景,粗线表示最大后悔值。

图5 x2∈(ci,ci+1]时最大后悔值Rmax(X(x2))的结构示意图Figure 5 Illustration of Rmax(X(x2)) where x2∈(ci,ci+1]
由于R(X(xk),s)=F(X(xk),s)-F(X(xopt(s)),s),根据前面的分析(引理9、引理10) 可知,在O(mn3) 时间可以得到F(X(xk),s)(对于所有xk∈和所有s∈D(xk)),F(X(xopt(s)),s)(对于所有s∈D) 可在O(m2n4) 时间求得(引理13)。那么R(X(xk),sj) (1 ≤j≤n) 通过O(n) 时间可得。记z*i∈(ci,ci+1]表示对于任意xk∈(ci,ci+1]都有≤Rmax(X(xk))。那么和可以通过建立线性规划模型求解。设H为变量,建立线性规划模型如下:
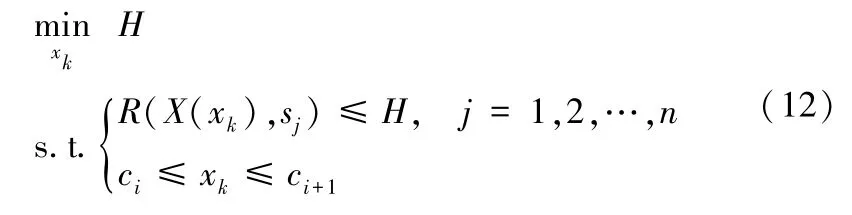
所以当xk∈(ci,ci+1]时,对于所有s∈D(xk),通过O(n)时间可得。因为边e=(vp,vq) 包含O(n)个区间,所以,对于边e=(vp,vq) 和所有s∈D(xk),通过O(n2) 的时间可得。
引理15对所有边e∈E,可以通过O(m2n4) 时间得到。
定理2一般网络图中,就近原则下新增应急避难点的鲁棒选址问题可以通过O(m2n4) 时间求解。
至此,一般图上新增应急避难点的最小最大后悔选址方案的求解算法归结如表2 所示。

表2 最小最大后悔选址方案求解算法Table 2 The minimax regret sink location algorithm
3 数值算例分析
这部分先给出一个数值算例并按步骤求解,以此展示本文多项式算法的求解过程。之后,基于权重区间的组距进行了敏感性分析,探讨最大完成时间的最大后悔值与不同顶点权重组距之间的关系。此外,采用各个顶点权重区间的中值(平均分布下的期望权重)作为各顶点的权重值进行选址,进一步比较中值场景下最优选址的最大后悔值与最小最大后悔值之间的关系。
3.1 算法求解示例
如图6 所示,一般网络图G=(V,E) 中包含9 个顶点,V={v1,v2,v3,v4,v5,v6,v7,v8,v9}。图中每条边的长度见标注在边上,|E|=17。图中各顶点的权重Wi=(1 ≤i≤9) 见各个顶点旁的区间值。图G中已有两个避难点x1和x2,x1位于顶点v6处;x2位于边(v4,v5) 上,其与顶点v4的距离为5。要在图G中再增加一个避难点x3使得最大完成时间的最大后悔值最小化。设单位权重在各路段上移动单位距离所需的时间τ=1,每条边具有相同的通行能力c,且c=1。算例分两部分求解该问题。首先找到所有的可能最坏场景,并计算各个可能最坏场景下的最优选址;然后分别计算新增应急避难点在顶点和边上的最优选址,最后比较两者最优后悔值的大小,确定整体最大后悔值最小的选址。
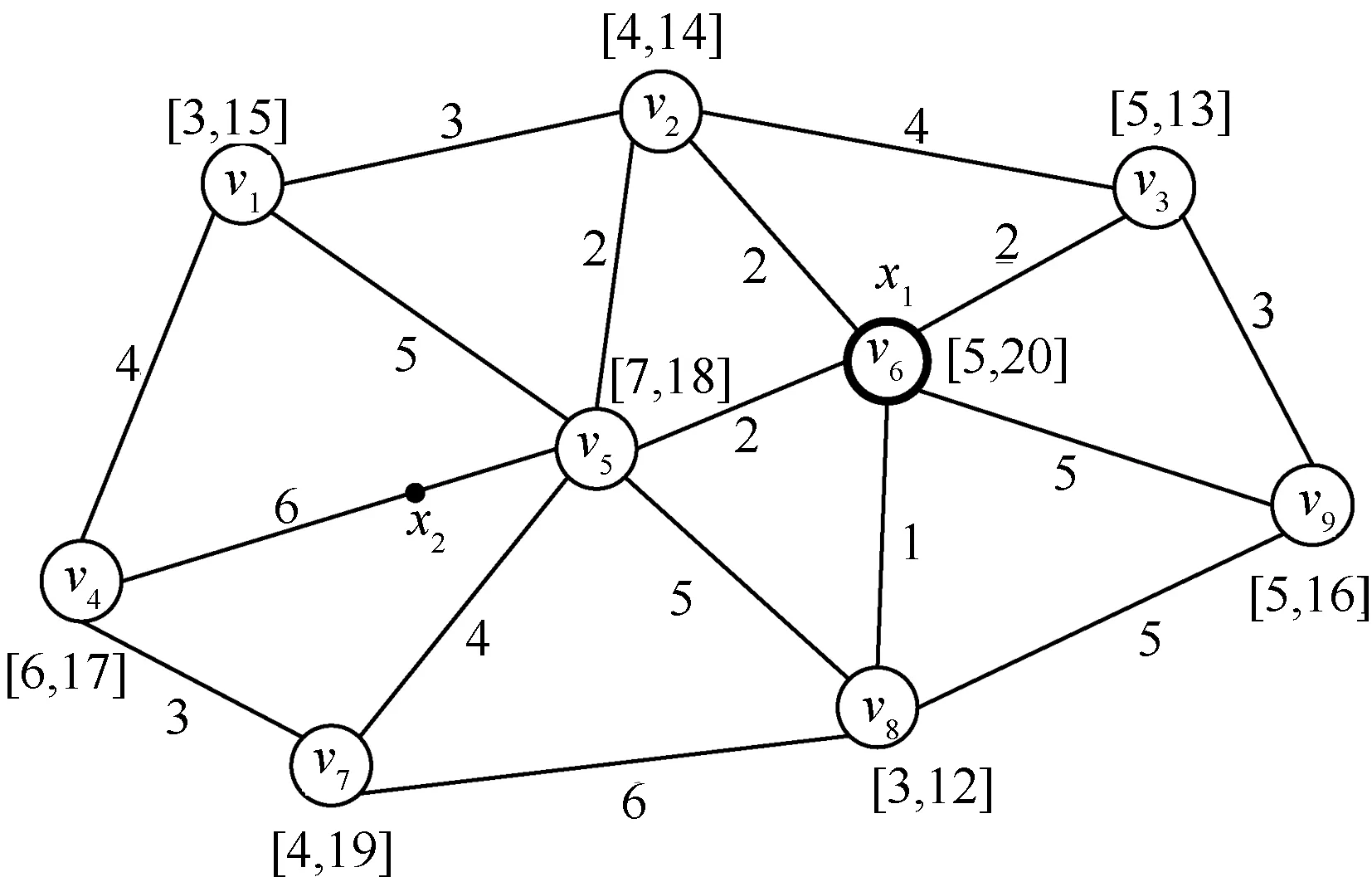
图6 一般网络示意图-1Figure 6 Example 1 of a general network
(1)计算所有可能最坏场景下的最优选址及撤退时间
首先,根据Floyd-Warshall 算法得到图G中任意两点之间的最短路径。然后,找到每个顶点初始选择的避难点和最短路径(如表3 所示)。最后,通过三步计算找到最优避难点和其对应的撤离完成时间:①找到边上的敏感点;② 找到所有的可能最坏场景;③计算所有可能最坏场景下的最优避难点及撤离完成时间。
通过表3,可以看到原来各个顶点选择的应急避难点及对应的疏散路径。其中选择应急避难点x1的顶点为{v1,v2,v3,v6,v8,v9},选择应急避难点x2的顶点为{v4,v5,v7}。

表3 各顶点初始选择的避难点和最短路径Table 3 The original sink point and evacuation route of each vertex
表4 给出了当x3选择不同位置时,网络图被划分为不同树图的分界点(称敏感点)。相邻敏感点之间最终形成的树图结构是一样的。
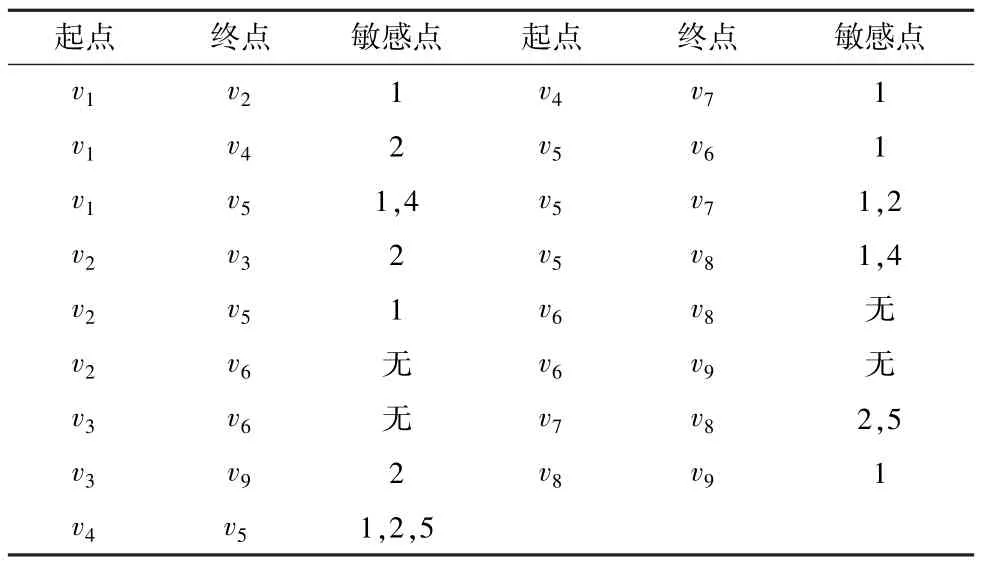
表4 图G 中各边上的敏感点Table 4 The sensitive points of G
表5 列出了所有可能的最坏场景。在该算例中,最终的可能最坏场景有12 个,即当x3选在不同位置时,使其后悔值最大的必然是其中一个场景。
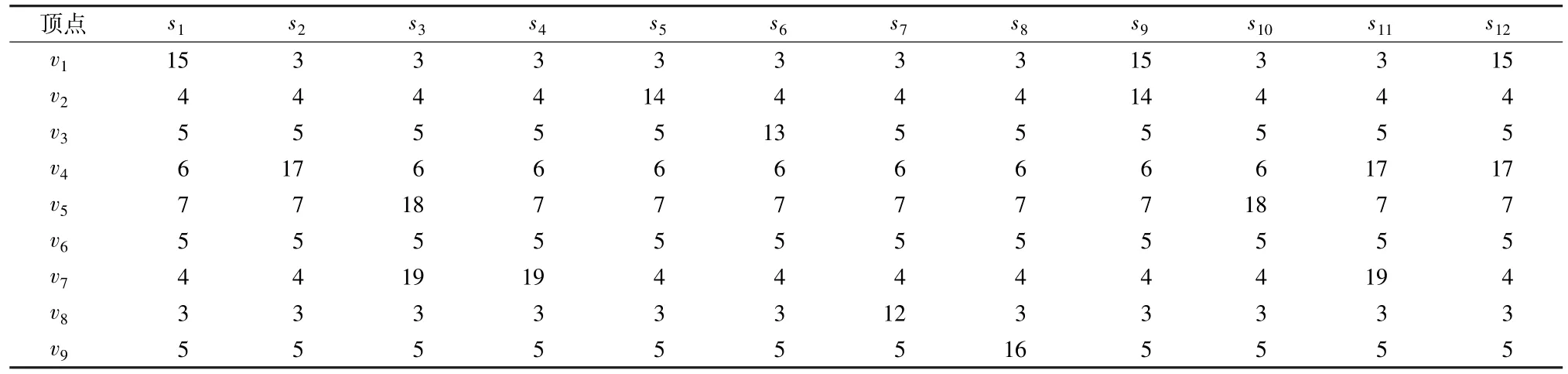
表5 所有的可能最坏场景Table 5 The potential worst case scenarios
表6 表示所有可能最坏场景下的最优选址对应的撤离完成时间,当x3选在不同位置时,不同最坏场景下的选址撤退时间与该场景下最优选址撤退时间之差则为后悔值。

表6 所有可能最坏场景下的最优选址对应的撤离完成时间Table 6 Optimal maximum completion times under potential worst case scenarios
(2)最大后悔值最小的避难点选址
把最坏场景限制在一个有限集合内,则可以计算x3选在不同位置时各个最坏场景下的后悔值,找出最大后悔值最小的位置。可能的选址位置分为两部分计算:
①当x3位于顶点时,通过计算每个场景下的后悔值,从而得到各顶点处的最大后悔值 (如表7 所示)。因此,由表7可得最大后悔值最小的避难点位于顶点v4处,其对应的最大后悔值为12。

表7 各顶点处的最大后悔值Table 7 The maximum regret of vertex location
② 当x3位于边上时,边上的敏感点将每条边分为若干个区间,在每个区间内通过线性规划的方法得到所有场景下最大后悔值最小的点z和其对应的最大后悔值(如表8 所示)。因此,由表8 可得最大后悔值最小的避难点位于边(v4,v7) 上,其与顶点v4距离为2.5,对应的最大后悔值为9.5。
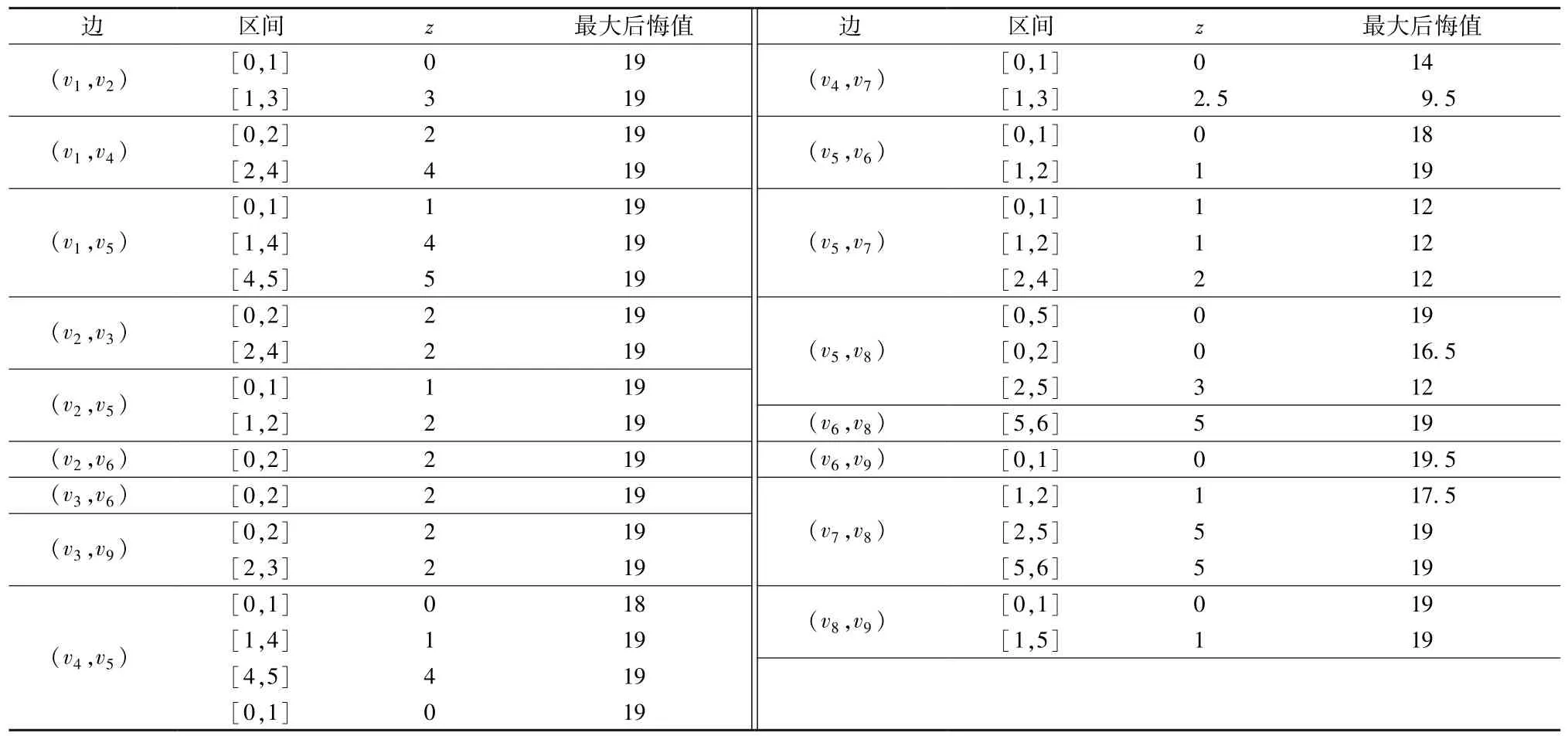
表8 各边所有场景下最大后悔值最小点zTable 8 The minimax regret locations of edges
通过比较表7 和表8 可以看出,图G中使得最大后悔值最小的避难点x3应当位于边(v4,v7) 上,其与顶点v4距离为2.5,对应的最大后悔值为9.5。
3.2 敏感性分析算例
这部分主要分析顶点权重的变化对选址结果的影响。具体包括:分析了三种不同组距变化情形下,最大完成时间的最大后悔值随顶点权重组距的变化情况;采用权重中值作为期望意义下的权重,分析该场景下最优选址方案与最小最大后悔选址方案的变化差异。以图7 所示的网络图为例,图中共有15 个顶点,各边上的数字表示该边的权重(长度);图中已有两个应急避难点,其中x1位于顶点v2上,x2位于边(v4,v7) 的中点。由于城市发展扩张,现需要在该网络图中新增一个应急避难点以使得新的最大完成时间的最大后悔值最小。
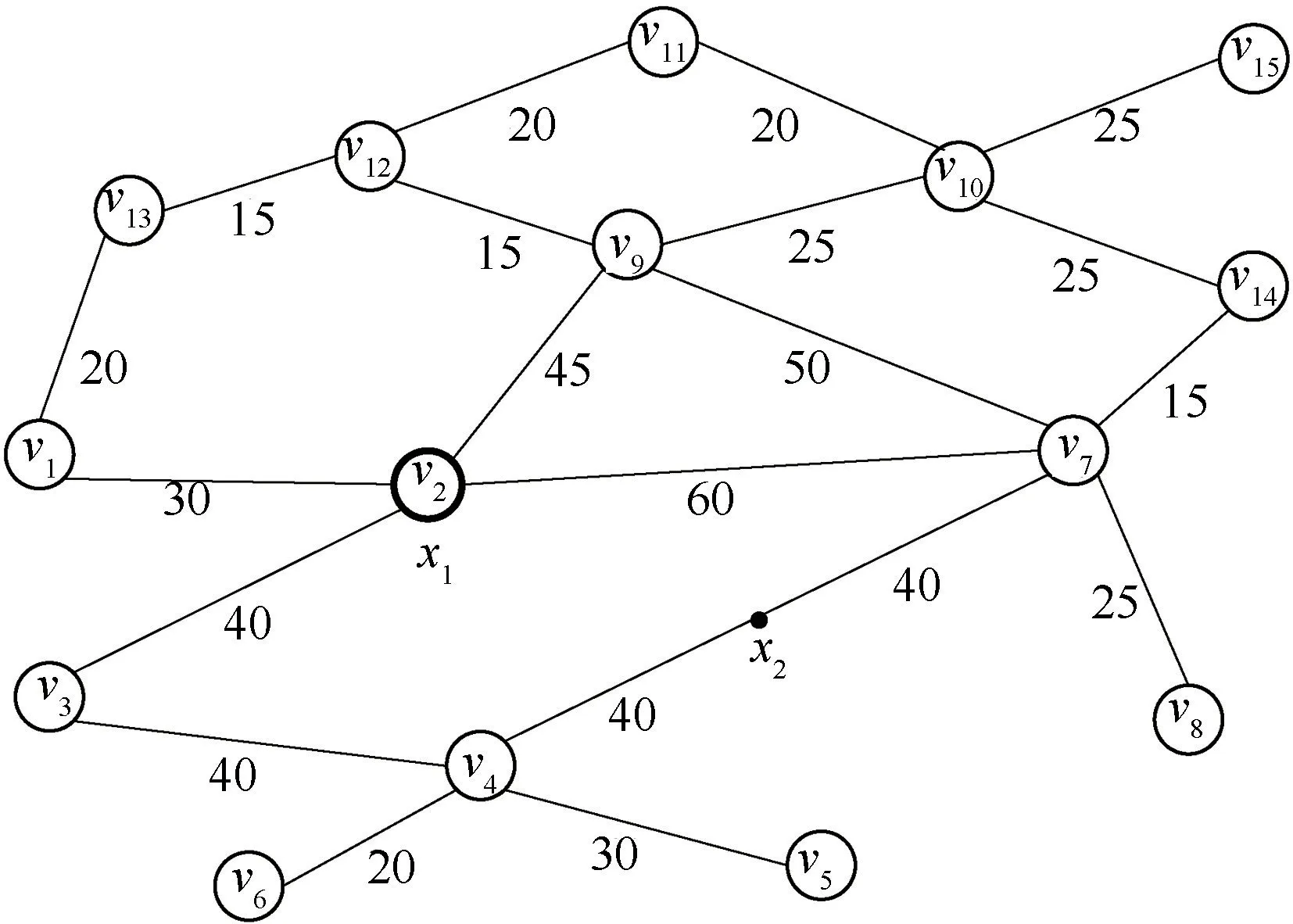
图7 一般网络示意图-2Figure 7 Example 2 of a general network
(1)限制最大组距的情形
称di=为顶点vi的对应的权重组距;称dmax=为最大组距。在这部分算例中,在不同的最大组距dmax限制下,为所有顶点随机生成权重区间(取整数),分别计算其对应的最小最大后悔值,计算结果如图8 所示。

图8 限制最大组距的最小最大后悔值变化示意图Figure 8 The minimax regret values with different dmax
根据算例结果可以看出,最小最大后悔值不会随着最大组距的增大而增大,即单纯的控制最大组距并不能有效的控制最小最大后悔值。
(2)权重组距相同的情形
在这部分算例中,各个顶点的权重组距相同,即对所有的顶点vi都有di=d,但各个顶点权重区间是不同的(随机生成)。在权重组距d变化时,分别计算对应的最小最大后悔值的变化;同时,假设采用各顶点权重区间的中值作为该顶点期望意义下的权重估计,计算期望的最优选址方案的最大后悔值。结果如图9 所示。

图9 不同组距下的最小最大后悔值及期望最优选址的最大后悔值变化示意图Figure 9 The minimax regret values and the maximum regtret of expected optimal locations with different d
在各点权重组距相同的情形下,最小最大后悔值随着组距的增加而增大,采用区间中值作为顶点权重时,最优选址方案对应的最大后悔值也是随着组距的增大而增大。通过对比最小最大后悔值与期望最优选址的最大后悔值可以发现,随着组距的减小,两者的差距也越来越小。
(3)权重组距不同的情形

图10 不同组距扩大值的最小最大后悔值及期望最优选址的最大后悔值变化示意图Figure 10 The minimax regret values and the maximum regtret of expected optimal locations with different dexp
在区间权重组距不同的情形下,当所有的权重组距同步增大时,最小最大后悔值也逐步增大。通过对比最小最大后悔值与期望最优选址对应的最大后悔值可以发现,随着权重组距的减小,两者的差距也越来越小。
通过以上三组算例分析可知,只优化最大组距并不能有效的减小最小最大后悔值,即关注于变化最大的疏散点的权重估计并不是好的方向,这是由于最小最大后悔值对应的最坏场景中不一定包含最大组距对应的顶点;但是,缩小所有顶点权重的组距则能够有效的减小最小最大后悔值,这是由于所有权重区间扩大后必然包括了未扩前所有的可能场景,也即包括了其最大后悔值场景。同时,当所有权重组距相对较小时,采用权重区间的中间值(权重平均分布的期望值)作为权重估计得到的最优选址的后悔值与最小最大后悔值接近,而当权重组距较大时,则两者差距明显;根据这个结果,在进行疏散点的权重估计时,达到一定的估计区间范围即可,不必一味地追求精准权重数据,在疏散点人流变化不太大的情况下,直接利用经验估计值作为该疏散点的权重也可以取得较好的效果。
4 结论
本文基于就近原则研究了新增应急避难点的选址问题。针对该问题,先通过敏感点的寻找,把一般图分解成基于不同敏感点的树图;而后分析各个树图的性质,找到所有的可能最坏场景;基于所有的可能最坏场景,找到避难点落在顶点时的最小最大后悔值选址点,采用线性规划的方法求解各条边上的最小最大后悔值选址点,最后比较得到整体的最小最大后悔值选址点。针对权重确定的情形,给出了计算复杂度为O(mn2) 的多项式求解算法;针对权重处于区间值的情形,设计了计算复杂度为O(m2n4) 的多项式求解算法。
通过数值算例分析可知(1)如果要达到有效减小最小最大后悔值的目标,只控制最大组距不能达到预期效果,即通过缩小单个权重的组距并不能有效的减小目标值,只能通过同时缩小所有顶点权重才能有效达成目标;(2)当权重组距较小时,用顶点权重区间的中间值替代区间权重,采用求解速度更快的确定性求解算法,可获得较好的效果;而当组距较大时,采用确定性求解算法求解,获得的结果与最优解差距较大,同时差距会随着组距的增大而增大。
由于新增多个应急设施问题是NP-难的,因此只能设计近似算法进行求解。在新增设施数量较小时,可结合本文对一般图的分解性质,基于组合数,采用本文的求解思想进行求解。在后续的研究中,可以针对道路通行能力不同的情形展开研究,优化目标除了考虑最大完成避难时间外,也将考虑各个应急避难点的负载均衡。

