基于CS-C-SVM的多参数GNSS欺骗干扰检测

卢 丹 殷亚强

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

1 引言

卫星导航服务在军用和民用领域有着广泛的应用，涵盖了国防安全、国民经济和人们日常生活的方方面面。但全球导航卫星系统（global naviga⁃tion satellite system，GNSS）信号发射功率小，在传播过程中易受到自然和人为的干扰，其中欺骗式干扰针对目标接收机发射欺骗信号，使其在无意识的情况下解算出错误的定位信息［1］。欺骗式干扰主要分为生成式和转发式两大类，生成式欺骗干扰利用民用信号结构体制公开的特点复制出与真实卫星信号格式一致的欺骗信号，转发式欺骗干扰是欺骗者通过接收设备接收真实卫星信号并将信号适当放大、延迟后转发给目标接收机，两者都具有干扰隐蔽性强且难以被检测的特点，会给被欺骗者造成难以估计的危害。

常见的欺骗干扰检测技术主要包括：利用欺骗信号功率大于真实信号功率的信号功率检测技术，但欺骗信号经过多径传输功率衰减后此方法的检测性能下降［2］；利用相关函数是否畸变的信号质量检测技术，当欺骗信号功率过大时会压制真实信号，此方法失效［3］；利用信号来向是否一致的多天线欺骗检测技术，但这种方法的实时性差［4］；利用惯性单元辅助的检测技术，此方法需要额外的高成本的设备，因而不能大规模应用［5］。上述几类检测技术仅利用一个参数检测欺骗干扰存在一定的局限性，综合考虑多个参数信息可以弥补单一参数的不足，将多个参数作为机器学习的特征输入，构建分类器，通过对信号分类达到检测欺骗干扰的目的。文献［6］中，Panice 等人开发出一个模拟系统，用于学习无人机遭受GPS（global posi⁃tioning system）欺骗攻击时的状态，并将支持向量机（support vector machine，SVM）作为检测异常状态的工具。文献［7］中，Sun 等人计算了欺骗信号和真实信号小波变换系数的奇异值，并把奇异值作为SVM 的特征输入。文献［8］中，Semanjski 等人计算所有GNSS 观测量之间的互相关系数，选择具有统计显著性的观测量作为SVM 的特征输入。文献［6-8］选择特征时很少关注接收机参数的变化，同时文献中使用网格搜索（grid search，GS）算法优化SVM，此方法容易陷入局部最优且需要较长的优化时间［9］。布谷鸟搜索（cuckoo search，CS）是基于布谷鸟寻巢和莱维飞行提出的一种元启发式算法，具有全局优化能力强且易于与其他算法耦合的特点，已应用于包括SVM 在内的多种优化问题。本文利用多个参数检测欺骗干扰，并将CS 应用于优化C-SVM，首先给出信号模型，信号在接收机中计算得到所用的参数，随后提出检测欺骗干扰的方法和优化过程，最后通过实验验证该方法的有效性。

2 信号模型

t时刻时，假设接收机接收到的信号为x(t)，则x(t)可表达为

式中，ς(t)为高斯白噪声，xa(t)代表真实卫星信号，xspo(t)代表欺骗信号，xmul(t)代表多径信号，xa(t)、xspo(t)和xmul(t)可分别表达为

其中，a、spo 和mul 代表真实、欺骗和多径，Q、U和Omul代表接收到的真实信号、欺骗信号和多径信号的数量，g(t)和c(t)代表导航电文和C/A 码，ψ代表信号幅值，τ代表传输时延，ω和θ分别代表载波频率和载波相位。

信号在接收机中经过不同的信号处理阶段，主要有捕获、跟踪和定位解算，在这些过程中可以计算得到表1列出的十个参数［10］。当接收机受到欺骗攻击时，不仅会引起载波多普勒频移、载噪比等参数变化，同时也会改变载波鉴相器误差标准差、接收机时钟偏差等接收机参数。例如，图1 和图2 画出了载波鉴相器误差标准差和载波多普勒频移未加欺骗干扰和在60～70 s 内加入欺骗信号的对比图，由图可知，加入欺骗信号后会使得这些参数产生变化，因此综合利用这些参数可以检测欺骗干扰［11-19］。

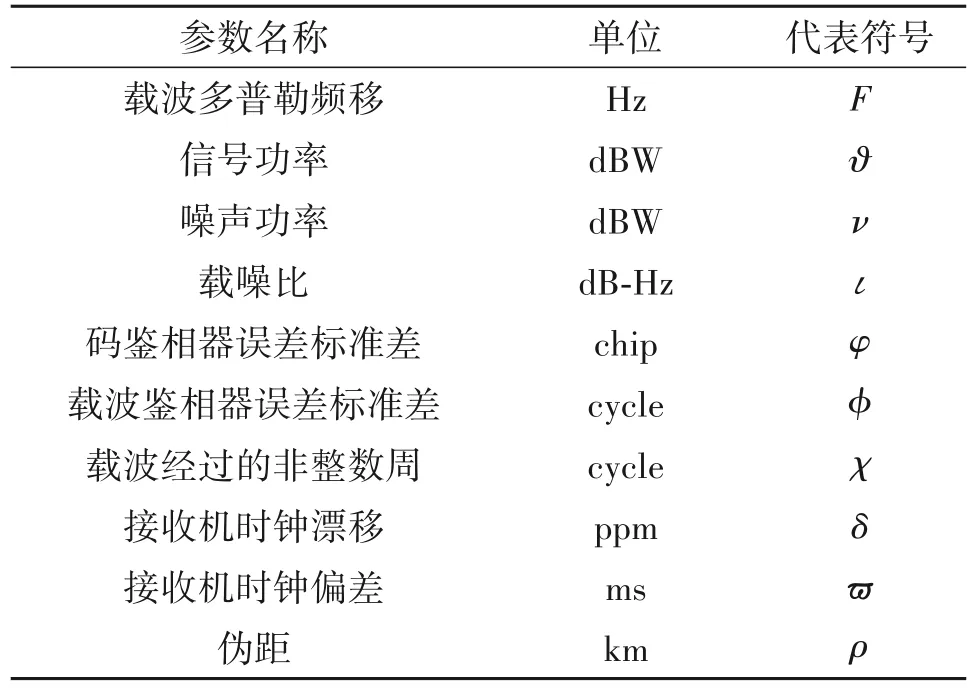
表1 参数列表Tab.1 Parameter list

3 基于CS-C-SVM的欺骗干扰检测算法

将表1 中的参数作为C-SVM 的特征输入，构建分类器，根据这些参数的变化对信号分类，从而判断出是否存在欺骗干扰。

3.1 C-SVM原理

假设训练集D={(di，li)|di∈R10，li∈{+1，-1}，i=1，2，…，N}，其中，di=(Fi，ϑi，νi，ιi，φi，ϕi，χi，δi，ϖi，ρi)代表第i个训练数据向量，li代表di对应的类别标签，类别标签为1 和-1 分别代表真实信号和欺骗信号，N代表训练集样本数量。基于C-SVM 的检测原理是通过一个具有最大间隔的分类超平面wTd+b=0 区分真实信号和欺骗信号，其中，w为分类超平面的法向量，b为分类超平面到原点的距离。由于训练样本非线性可分，使用映射函数κ(⋅)将其从原始空间映射到一个更高维的特征空间中，从而使训练样本在特征空间中获得更高的分类准确率［20］，可将这个过程表示为形如式（5）的优化问题［21］

其中，C为惩罚系数，ξi是允许出现分类误差的松弛因子。引入拉格朗日乘数法得式（5）的拉格朗日函数

αi≥0，βi≥0为拉格朗日乘数因子，令式（6）对w，b，ξi的偏导为0可得

把式（7）～（9）代入式（6）得

式中，J(di，dr)代表径向基核函数，表达式如下所示

γ为核函数的带宽。由于式（10）恒小于等于式（5），则原优化问题式（5）的对偶形式如下所示［21］

给定γ和C可以求解出一组αi，即可确定一个分类器，为确定最优的分类器模型，需要通过优化算法搜索出C-SVM 最优的参数γopt和Copt，根据优化算法改变γ和C的值构建不同的分类器，对验证集分类，分类误差率最小时对应的γ和C即为γopt和Copt。

其中，PV和E代表验证集的分类准确率和分类误差率。GS 是一种简单易实现的优化算法，GS 优化CSVM的示意图如图3所示。

确定γopt和Copt后，通过序列最小优化方法求解式（12）得到αi，利用αi构建分类器f，f的表达式如下所示

其中，αi满足αi>0 时与其对应的di代表支持向量，Nsv代表支持向量的数量，hm代表测试集W={hm|hm∈R10，m=1，2，…，M}中的第m个测试数据向 量，hm=(Fm，ϑm，νm，ιm，φm，ϕm，χm，δm，ϖm，ρm)，M代表测试集样本数量，则分类结果可表达为

3.2 CS优化C-SVM

由图3可知，GS算法只在设定点处搜索γ和C且搜索步长和方向是固定的，容易陷入局部最优解，而CS通过莱维飞行更新搜索步长和搜索方向并且结合了局部搜索和全局搜索可以克服这一问题［22］。将CS应用于优化C-SVM，假设代表第n次迭代中的第k个优化方案，n=1，2，…，Imax，Imax代表最大迭代次数，zopt=(γopt，Copt)代表最优方案，优化步骤归纳如下：

步骤1初始化一组优化方案Z0={z0k|k=1，2，…，K0}。

步骤2把每一个优化方案作为C-SVM 的参数构建分类器并对验证集分类，寻找分类误差率最小时对应的γ和C，记录为当前最优方案。

步骤3根据莱维飞行公式更新一组优化方案进入全局搜索模式，更新方式符合式（16）［23］。

其中，K n-1代表第n-1 次迭代完成后优化方案的数量，μ为步长比例因子，更新后的优化方案，G(η，λ)为莱维随机搜索路径，λ为1 至3 内的任一值，η=(ηγ，ηC)代表搜索步长，ηγ和ηC分别代表γ和C的更新长度，G(η，λ) 的表达式如下所示

使用更新后的一组优化方案Zn重复步骤2。

步骤4在Zn中根据概率P随机舍去部分优化方案，同时根据式（18）补充一部分新的优化方案进行局部搜索，将局部搜索得到的最小分类误差率与步骤3 得到的最小分类误差率比较，得到第n次迭代的最优方案

式中，ε为一个服从均匀分布的随机数，H(⋅)为单位阶跃函数，⊗为叉乘运算，为两个不同的随机优化方案。

步骤5比较和第n-1 次迭代的最优方案，两者之间的更优方案即为最优方案zopt，若此时达到最大迭代次数，输出最优的方案，否则重复步骤3。

CS在局部搜索和全局搜索之间达到了平衡，有效避免了GS 优化C-SVM 陷入局部最优的问题。在分析了原理和关键步骤之后提出完整的欺骗干扰检测算法，如图4所示。

4 仿真实验

模拟17 颗卫星发射的信号，考虑多径的影响，在信号中加入信噪比为-22 dB、延迟为0.8 码片的多径信号。信号在接收机中处理后采集十个参数，利用17颗卫星的十个参数共同构造训练集，训练集共包含48000个样本，仿真参数如表2所示。

表2 训练集仿真参数表Tab.2 Training set simulation parameters table

利用GS和CS分别搜索γopt和Copt，γ和C的搜索范围均设置为［0.015，2］和［0.0625，8］。CS 算法中，初始优化方案数量设置为20，最大迭代次数为30，P为0.25，λ为1.5。CS 搜索出的γopt和Copt为0.8583 和0.9891，GS 搜索出的γopt和Copt为0.9659和1。利用得到的两组γ和C构建两个分类器，通过实验分析不同情况下检测欺骗干扰的性能。

首先测试了不同干噪比的检测性能，每一个干噪比对应一个测试集，干噪比的范围为-18 dB至-2 dB，每个测试集中包含了1600 个真实信号和4800 个欺骗信号，测试集的分类准确率和虚警率如图5 和图6 所示，对比两种方法的实验结果，CS-CSVM 方法的准确率至少提高了0.16%且虚警率至少降低了0.62%。由图5 和图6 可知，利用本文方法检测欺骗干扰时，对于小干噪比的欺骗信号，即欺骗信号功率和真实信号功率相差较小时，准确率达到了96%以上，随着干噪比逐渐增大，载噪比等参数会逐渐增大，准确率逐渐增大且虚警率逐渐降低。文献［3］中，作者利用SQM 方法检测欺骗干扰，当干噪比比真实信号的信噪比大10 dB 时，SQM 方法已很难检测到欺骗干扰。以序号为1 的卫星为例，在60 s 至70 s 内加入干噪比比信噪比大10 dB的欺骗信号，分别利用SQM 算法和本文算法检测欺骗信号，每次检测的信号数量为1000 个，虚警率设置为0.01，检测结果如表3 所示，由表3 可知，本文算法在SQM失效时仍具有良好的检测性能。

表3 本文算法和SQM算法准确率对比列表Tab.3 Comparison list of the accuracy of the algorithm in this article and the SQM algorithm

其次测试了不同码延迟的检测性能，每一个码延迟对应一个测试集，码延迟的范围为0.5 码片至10 码片，每个测试集中包含了1600 个真实信号和4800 个欺骗信号，测试集的分类准确率和虚警率如图7 和图8 所示，对比两种方法的实验结果，CS-CSVM 方法的准确率至少提高了0.03%且虚警率至少降低了0.12%。当码延迟小于1 码片时，多峰检测方法不能较好地区分真实和欺骗信号，本文算法通过载波鉴相器误差标准差和码鉴相器误差标准差等参数的变化可以检测出欺骗干扰的存在，由图7 可知，当码延迟为0.5 码片和1 码片时，准确率达到了96.29%和98.34%，对于较大延迟的欺骗信号，准确率可以达到99%以上。对比三个检测方法的复杂度，并以一颗星为例，检测1000个信号，计算三种算法所需的运算量，结果如表4所示，其中，ωsqm、Ksqm、Nsqm、Speak、Npeak、dR、Nsv和M分别代表滑窗长度、卫星数量、信号数量、累加次数、点数、参数数量、支持向量个数和测试样本数。虽然本文方法运算量大于其他两种检测方法，但弥补了多峰检测和SQM 方法在检测小延迟和大功率欺骗信号时的不足。

表4 算法复杂度和运算量对比列表Tab.4 Comparison list of algorithm complexity and calculations

表5和表6列出了两个分类器对时延为10码片的测试集分类后的混淆矩阵，由表5 和表6 可知，两种方法中欺骗信号被全部检测出来，GS-C-SVM 方法中有13 个真实信号被错误分类为欺骗信号，而CS-C-SVM 方法中被错误分类的真实信号减少到6个。

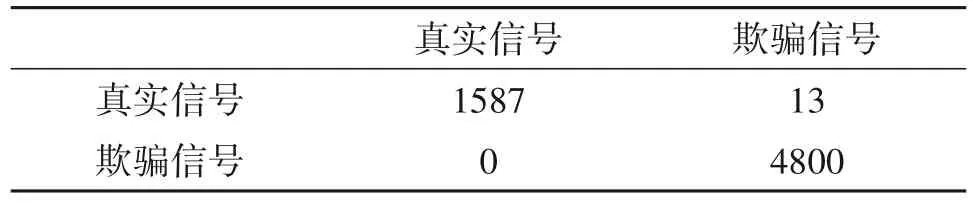
表5 时延为10码片时的GS-C-SVM分类结果的混淆矩阵Tab.5 Confusion matrix of GS-C-SVM classification result of ten chips delay

表6 时延为10码片时的CS-C-SVM分类结果的混淆矩阵Tab.6 Confusion matrix of CS-C-SVM classification result of ten chips delay

表7 总结了CS-C-SVM 和GS-C-SVM 的优化时间和分类时间，由表7可知CS-C-SVM的优化时间和分类时间为1680281 ms 和187.7 ms 均低于网格搜索优化的C-SVM，这表明CS-C-SVM 有着更高效的优化能力和更短的分类时间。

表7 实验总结Tab.7 Experiment summary

5 结论

本文将多个参数作为监督机器学习的特征输入，提出了基于CS-C-SVM 的多参数欺骗干扰检测方法，通过仿真实验验证了该方法的有效性，实验结果表明所用参数可以有效地指示是否存在欺骗干扰，同时综合利用这些参数可以在不同情况下检测欺骗干扰。CS-C-SVM 避免了GS-C-SVM 易陷入局部最优的问题，缩短了优化时间，提高了分类准确率并降低了虚警率。但对小干噪比和小延迟的测试集分类时，存在一定的虚警率，针对这一问题，将会在接下来的工作中重点研究。