频率安全分段控制下轮次切负荷协调优化策略

秦 川，任 伟，江叶峰，熊 浩，徐 贤，鞠 平

（1. 河海大学能源与电气学院，江苏南京 211100；2. 国网江苏省电力有限公司，江苏南京 210000）

0 引言

近年来，我国电网中远距离输电与大规模新能源发电比例迅速提升。远距离输电时有故障发生，新能源则具有随机性和间歇性。两者叠加，既显著增加了系统的不平衡冲击，又削弱了系统的频率支撑能力，电网频率安全问题日益严峻［1-6］。

为了应对频率安全风险，需要充分挖掘电网中可暂时中断负荷参与频率调控的潜力，实现功率控制模式从传统的电源主导转向电源与负荷相结合，电网应急处理模式从被动的粗放式拉闸限电转变为主动的源荷平衡控制［7-11］。例如我国部分电网已经建成了采用分层控制架构的大规模精准负荷控制系统［10-11］，控制精度可以达到用户下的1个分路开关上的可中断负荷量。通过主动快速切除可中断负荷，迅速遏制频率下滑，避免被动慢速切除负荷造成的大量损失。

在实施负荷控制时，首先要从系统层面设计控制策略，确定负荷控制总量以及下层各个负荷节点（或负荷控制子站［10-11］）的负荷控制量［7-11］。现有的负荷控制研究主要集中于这一层面，如基于灵敏度分析的负荷控制优化策略［12］、分区分层优化负荷控制策略［13-14］、协调经济性与事故评级的负荷控制策略［15］等。文献［7，16］提出了频率安全分段控制策略，该策略以频率最低点为界，频率最低点前为频率安全控制Ⅰ段（FC-Ⅰ段），频率最低点后为频率安全控制Ⅱ段（FC-Ⅱ段）：在FC-Ⅰ段通过直流调制、毫秒级负荷控制等手段，将最低频率控制在允许频率以上；在FC-Ⅱ段通过秒级／分钟级负荷控制、自动发电控制（AGC）等，将频率恢复值、电源备用水平等控制在允许范围内。

在系统层面确定负荷节点（或负荷控制子站）的负荷控制量后，需要进一步将该控制量进行分解，确定底层各个用户的可中断负荷切除量［17-23］，并通过负控终端实施负荷切除（精确到用户的分路开关）。现有的研究和工程实践主要是对用户的可中断负荷按照重要程度、负荷类型等原则进行分类、分级排序，并在实施控制时按照最小控制误差原则进行层级匹配、分布切除［17-19］，而较少考虑经济性。此外，文献［20-23］考虑电网与用户、多用户之间的博弈互动，建立负荷切除、需求响应优化模型。这一类博弈模型一般优化求解时间较长，难以应用于毫秒级负荷控制。且上述研究往往仅考虑了单次负荷切除，未考虑频率分段控制时的负荷切除多轮次协调。

为此，本文提出了频率安全分段控制下的可中断轮次负荷切除优化策略：在FC-Ⅰ段，重点保证毫秒级负荷控制的精准快速性；根据FC-Ⅰ段策略确定的节点负荷控制量，以控制代价最小为目标，基于McCormick 松弛和内点法，快速求解该节点下底层用户的毫秒级负荷优化切除策略；在FC-Ⅱ段，综合考虑FC-Ⅰ段后的剩余可控量与用户的参与意愿，建立多用户非合作博弈模型，并采用多目标粒子群优化（MOPSO）算法求解秒级／分钟级负荷切除方案。最后，通过实例分析验证了所提策略的有效性。

1 频率控制分段与负荷轮次切除

1.1 频率安全分段控制

电网某次大功率缺额故障下的频率动态响应如图1 所示［5］，此过程可以大致分为2 个阶段。第一阶段为频率下降阶段，即在发生大功率缺额后到频率最低点之间的时间段，这一阶段起始频率下降速度较快，然后随着一次调频等控制措施的作用而变缓。第二阶段是频率回升阶段，随着各种调频资源的投入，频率从最低点开始回升直至平稳状态。

图1 频率动态响应过程Fig.1 Process of frequency dynamic response

根据频率动态响应的不同时段，可以设计不同的控制目标，进行频率安全分段控制［7，16］。第一阶段的控制（FC-Ⅰ段）主要是为防止频率快速下跌，通过直流调制、毫秒级负荷控制等手段，将最低频率控制在允许频率以上；第二阶段的控制（FC-Ⅱ段）主要是为了消除FC-Ⅰ段后系统仍然可能存在的静态频率、电压偏低，以及部分线路过载的问题，可以通过秒级／分钟级负荷控制、AGC等手段，将频率恢复值和电源备用水平等控制在允许范围内。

1.2 毫秒级与秒级／分钟级负荷切除的协调

在系统层面，根据频率安全分段控制策略确定各个节点的控制量后，需要在负荷节点（或负荷控制子站）层面进一步将该控制量进行分解，确定底层各个用户的可中断负荷切除量，并通过负控终端实施负荷控制。

由于响应时间短，FC-Ⅰ段的毫秒级负荷切除主要追求经济性、有效性和快速性，一般不考虑用户的参与意愿。因此，FC-Ⅰ段紧急负荷控制拟采用计算速度快的线性规划等优化算法求解负荷切除方案。

FC-Ⅱ段的决策时间相对宽裕，可以达到秒级或分钟级。在这一过程中，可以充分考虑FC-Ⅰ段后的剩余负荷可控量以及用户的参与意愿（例如部分用户在FC-Ⅰ段已经被切除一部分负荷），使FC-Ⅱ段秒级／分钟级负荷控制的措施配置更为合理，并在一定程度上弥补FC-Ⅰ段的负荷控制方案造成的消极影响。因此，秒级／分钟级负荷切除策略考虑用户意愿，进行用户间非合作博弈。频率安全分段控制下的轮次切负荷框图如图2所示。

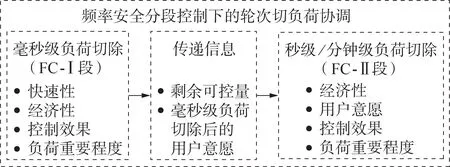
图2 频率安全分段控制下的轮次切负荷协调Fig.2 Wheel load shedding coordination under frequency safety subsection control

2 毫秒级负荷切除优化策略

在FC-Ⅰ段，基于毫秒级负荷切除防止频率快速下跌。因此，以经济代价最小为目标，以切负荷精确度、切负荷量、负荷重要程度为约束，建立毫秒级负荷切除优化模型。

2.1 可中断负荷的多重属性分类

可中断负荷具有多重属性，在FC-Ⅰ段，毫秒级负荷切除优化模型主要考虑负荷重要程度、负荷切除经济代价以及切除相关负荷的频率控制效果。

1）重要程度。

电力负荷根据供电可靠性及中断供电在政治、经济上所造成的损失或影响的程度，拥有不同的重要程度。在现有的精准负荷控制系统中，一般将负荷用户以及其下的各个分路开关，按照不同行业性质、重要程度等进行分档分级，档位、级别低者优先切除。

2）经济代价。

根据文献［24］，一般情况下，负荷用户切除成本与切除量呈二次函数关系，如式（1）所示。

式中：c(x)为负荷用户切除成本；k1—k3为常系数，由行业类型决定；x为中断容量。

此外，参考现有的负荷控制成本补偿方式，在式（1）中进一步加入电网与用户可中断协议中的补偿系数k4，则负荷用户切除成本与切除量的关系变为：

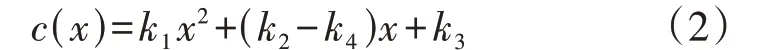
2.2 目标函数

毫秒级负荷切除的目标为经济性最优，如式（3）所示。

式中：i表示负荷用户下的分路开关i；xi为0-1 逻辑值，取值为0、1 分别表示切除分路开关i响应、不响应切除；ΔPi为分路开关i的可切容量；ci为分路开关i的单位切除代价；ρi为分路开关i的参数聚合系数；N为参与切除的负荷用户分路开关总数。

2.3 约束条件

根据可中断负荷的多重属性分类，毫秒级负荷切除的约束条件主要包括切负荷精确度约束、切负荷量约束以及负荷重要程度约束。

1）切负荷精确度约束。

将FC-Ⅰ段确定的节点控制量下发到底层各个负控终端实施负荷切除时，由于各可切单元为离散的、数额大小不一的用户分路开关，实际切除过程中往往存在欠切或过切的问题，因此在模型中加入切负荷精确度约束，如式（6）所示。

式中：ΔP为电网下达的负荷切除需求量；β为切负荷精确度要求值，由于实际系统具有一定的调节能力，能够承受一定程度的欠切或过切，因此β只要小于某一阈值βmax（可根据实际系统推算或经验确定），就能使频率恢复稳定。

2）切负荷量约束。

当电网发生频率故障，上层所下达的指令不应超过下层所有子站或终端可中断负荷总量，如式（7）所示。

3）负荷重要程度约束。

在负荷切除过程中，重要程度高的负荷应滞后切除，如银行、重要工厂、大型场地等；重要程度低的负荷应优先切除，如小型作坊、城市景观灯等。为了定量描述负荷的重要程度，借鉴专家经验法，通过对分路开关分级给出重要程度的量化描述，例如分为级别1—S，级别1 至级别S表示重要程度依次降低，重要程度低的分路开关优先切除，可表示为：

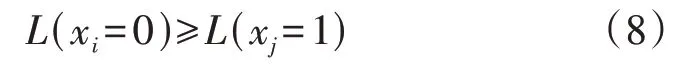
式中：i，j=1，2，…，N；L（·）为分路开关级别，L（·）∈{1，2，…，S}，L(xi=0) 表示参与切除的分路开关i的级别，L(xj=1)表示不参与切除的分路开关j的级别。

2.4 求解算法与优化流程

由于模型中考虑了实际电网按负荷重要程度的分级约束条件，为混合整数非线性规划（MINLP）问题。为此，采用McCormick 方法［25］将MINLP 问题松弛为凸非线性规划（NLP）问题，然后采用内点法进行快速求解。

式（8）所示负荷重要程度约束可以转换为多个乘式相加为1 的约束。考虑到一般性推导较为复杂，本文以S=2，即假设所有分路开关重要程度分为2级为例进行推导说明。

设db(b=1，2)为布尔值，表示优化过程中是否切除到级别b的分路开关，即db=1、db=0 分别表示切除、未切除级别b的分路开关。则当S=2 时，负荷重要程度约束可表示为：

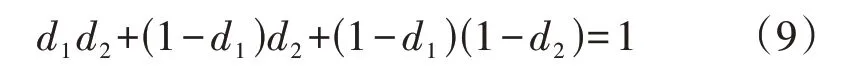
对于式（9）中的某个乘式w，令x、y分别表示乘式中的2个相乘项，采用McCormic方法可表示为：

式中：xU、xL和yU、yL分别为x和y的上、下限。

令a=x-xL，b=y-yL，则ab≥0，从而有：

式（12）表示w=xy的一个低估因子，经过相似推导，可得到另一低估因子和2个高估因子。

最终乘式转化为：

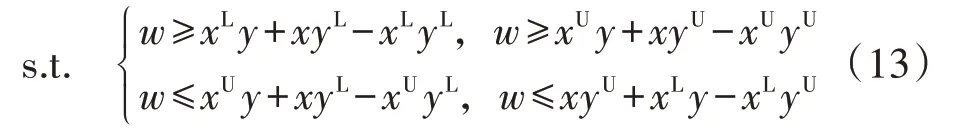
由此，式（3）—（8）所示的MINLP 问题被松弛为凸NLP 问题，可以采用内点法快速求解。毫秒级负荷切除优化流程图见附录A图A1。

3 秒级／分钟级负荷切除博弈策略

在FC-Ⅱ段，基于秒级／分钟级负荷切除将频率恢复值和电源备用水平等控制在允许范围内。在此过程中，各负荷用户之间互为竞争关系，各用户均希望切除更少且重要程度更低的负荷，尤其是在毫秒级负荷切除过程中已切除部分负荷的用户，这种行为关系是一种典型的非合作博弈。为此，本节建立秒级／分钟级多用户非合作博弈模型。

3.1 博弈要素

博弈论主要研究公式化了的激励结构间的相互作用，是研究具有斗争或竞争性质现象的数学理论和方法。其主要包含4 个博弈要素：参与者、策略、得失以及均衡。

1）参与者。

参与者是一个博弈的决策主体，参与者的目的是通过自身的选择或行动使自身的利益最大化。在秒级／分钟级多用户非合作博弈中，参与者为用户，各用户在电网下达指令后，均倾向于选择合适的策略使自身的负荷切除损失代价最小。

2）策略。

3）得失。

一局博弈结束时的结果称为得失。一局博弈结束时每个参与者的得失是全体参与者所取定的一组策略的函数，通常称为支付函数，将支付函数记为ul(Y)。秒级／分钟级多用户非合作博弈模型将每个用户的负荷切除损失代价和用户切除意愿作为支付函数，其中用户切除意愿与第1 轮毫秒级负荷切除时用户是否参与响应有关，表示为ul(Y)=Vl+Wl。其中：Vl为负荷用户l的负荷切除损失代价；Wl为负荷用户l的不满意度函数；Y为所有负荷用户已选的策略集，Y={Y1，Y2，…，Yl，…，YM}，Yl⊂Sl，Yl为负荷用户l在博弈中选用的策略，M为参与博弈的负荷用户总数。

4）均衡。

如果任意一位参与者在其他所有参与者的策略确定的情况下，其选择的策略是最优的，则这个组合就被定义为纳什均衡。在秒级／分钟级多用户非合作博弈模型中，当任意一负荷用户在其他负荷用户策略确定的情况下，无论如何改变其策略，都无法降低其支付函数时，非合作博弈便达到纳什均衡状态，所有博弈用户的策略选择集合成为纳什均衡解，记作Y*，其数学描述如式（14）所示。

3.2 非合作博弈多目标优化模型

在M个负荷用户的博弈当中，每个参与者都以其支付函数最小为目标相互博弈，最终达成纳什均衡。为了更加理性客观地得出结果，将非合作博弈模型转化为多目标优化问题。

1）目标函数。

在非合作博弈多目标优化模型中，优化目标为各用户支付函数最小，如式（15）所示。

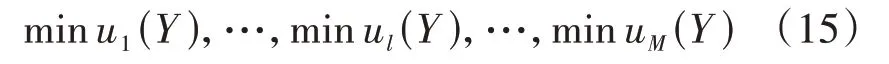
负荷用户l的负荷切除损失代价如式（16）所示。

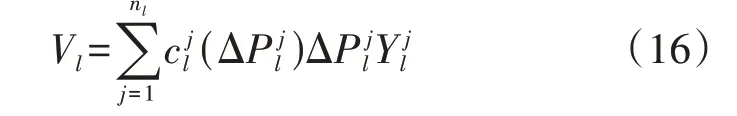
式中：nl为负荷用户l下的分路开关个数；Δ为负荷用户l下分路开关j的可切容量；为负荷用户l下分路开关j的单位切除损失代价表示负荷用户l所选策略对分路开关j是否进行切除，取值为1、0分别表示切除、不切除。

在第1 轮的毫秒级负荷切除过程中，切除量占用户可切除总量越多的负荷用户更不愿意参与第2轮的秒级／分钟级负荷切除。Wl是一个对负荷用户l在毫秒级切负荷过程中的切除比例逐渐递增的函数，且增速随着比例的增加而逐渐加快［26］，当负荷用户l未参与毫秒级切负荷时，Wl设为0。为此，构建了如式（17）所示的不满意度函数。

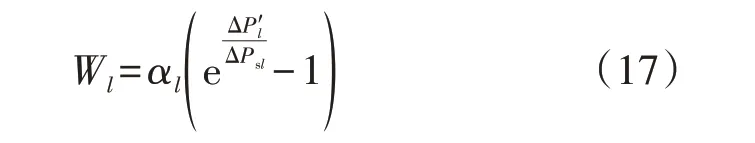
式中：ΔP′l为负荷用户l在第1 轮毫秒级切负荷过程中的切除量；ΔPsl为负荷用户l的总可切量；αl为对负荷用户l不满意度的重视程度，αl越大，表示越重视其不满意度。

2）约束条件。

与毫秒级负荷切除优化模型类似，非合作博弈多目标优化模型含有3 个约束条件：切负荷精确度约束、切负荷量约束以及负荷重要程度约束。

（1）切负荷精确度约束可表示为：

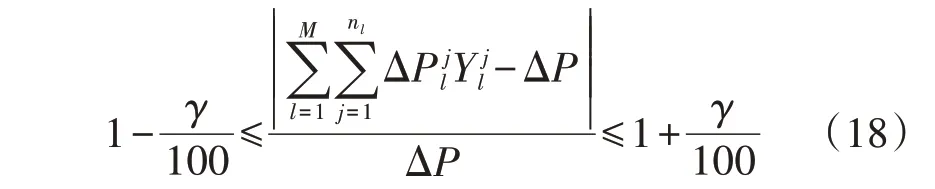
式中：γ为秒级／分钟级切负荷精确度要求值，γ∈(0，γmax)，γmax为电网所能承受的欠切或过切阈值。

值得说明的是，切负荷精确度约束为强约束，在其作用下，能保证切除量一定满足电网下达的切除指令要求，从而保证FC-Ⅱ段的调频效果满足要求。

（2）切负荷量约束可表示为：

（3）负荷重要程度约束可表示为：

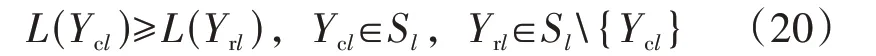
式中：Ycl为负荷用户l在博弈中所选择的策略；Yrl为负荷用户l在博弈中未选择的策略。

需要说明的是，切负荷精确度约束的优先程度高于负荷重要程度约束，当两者发生冲突无法得出纳什均衡解时，优先满足切负荷精确度约束。

3.3 求解算法与优化流程

求解算法采用MOPSO 算法，MOPSO 算法通过建立存储集不断更新粒子群位置，采用自适应网格法得到满足多个目标的非劣解集，即满足纳什平衡的解集。得出解集后，需要根据电网要求从中选出最合适的负荷切除方案。

秒级／分钟级负荷切除流程图见附录A图A2。

4 算例分析

4.1 算例设置

算例采用某地区电网的实际用采数据，包含50个负荷用户，每个负荷用户下的分路开关数量范围为1—10，总可切量为700 MW。在FC-Ⅰ段，确定的毫秒级负荷切除量为100 MW，秒级／分钟级负荷切除量为250 MW。此地区的负荷用户主要分为机械、电子、食品医药、建材和纺织类，根据不同的行业类型及专家借鉴经验，设置负荷切除损失代价的常系数如表1所示。

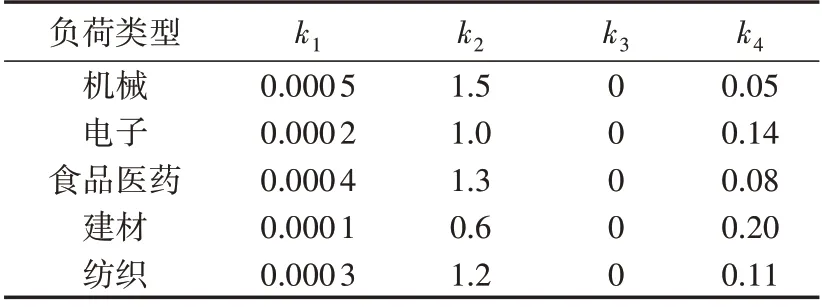
表1 负荷切除损失代价常系数的设置Table 1 Setting of constant coefficients of load shedding loss cost

4.2 毫秒级负荷切除算例

为了验证本文基于经济性最优的毫秒级负荷切除策略的有效性，在式（3）的基础上进一步考虑负荷的有功-频率特性系数KL。理论上，切除负荷的KL越小，则在频率跌落时负荷功率下降越少，频率控制效果越好。不同负荷类型对应的KL值如附录B 表B1所示。

为此，考虑以下3种目标函数。

1）仅考虑经济性最优，即目标函数为式（3）。

2）以KL最小为目标，对应的目标函数为：

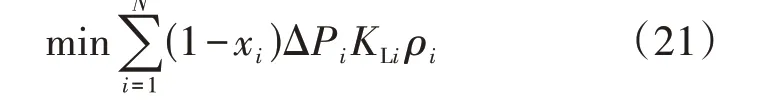
式中：KLi为分路开关i的有功-频率特性系数。

3）经济代价与有功-频率特性系数的权重各为50%，对应的目标函数为：

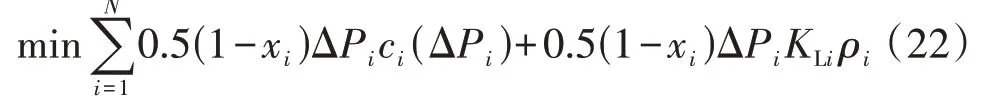
应用毫秒级负荷切除优化模型分别求解3 种目标函数下的负荷切除方案，在BPA 中搭建39 节点系统详细模型，并进行暂态仿真。仿真得到3 种负荷切除方案下的频率响应曲线，如图3 所示。图中方案1—3分别以式（3）、（21）、（22）作为目标函数。由图可见，在3 种负荷切除方案下，频率最低点最大相差0.000 7 Hz，稳态频率一致，可以认为其频率控制效果基本一致。

图3 3种负荷切除方案的频率控制效果对比Fig.3 Comparison of frequency control effect among three load shedding schemes

切除100 MW 负荷时，由3种不同的目标函数得到的负荷切除方案的负荷切除损失代价对比如表2所示。由表可见，在目标函数中的KL所占的权重越大，负荷切除损失代价越大。

表2 不同目标函数下的负荷损失代价Table 2 Load shedding loss cost under different objective functions

βmax在此算例中被设置为3，即所得负荷切除策略允许有±3%的浮动区间，切负荷精确度也可以作为一项负荷切除策略的考核指标。因此，在同样切除100 MW 的前提下，对最终的负荷切除策略的切负荷精确度进行计算比较。3 种目标函数下的切负荷量占电网下达指令的比例分别为0.970 0、0.970 3和0.9709，其最大差距不超过1‰。

本文在AMD 5600X CPU、32 GB 内存、512 GB硬盘的硬件条件下，基于MATLAB 平台，采用内点法计算毫秒级负荷切除策略的求解时间为17 ms 左右。根据文献［7］，江苏电网大规模精准负荷控制系统毫秒级负荷控制时间为245 ms（从故障发生到整组负荷切除）。因此，即使计及负荷切除策略计算时间17 ms，毫秒级负荷控制时间仍可以保持在300 ms以内，验证了本文方法在求解时间上对于FC-Ⅰ段频率控制问题的适应性。

综合频率控制效果对比、负荷切除损失代价对比以及切负荷精确度对比，在3 种目标函数下，频率控制效果基本一致，精确度差距不超过1‰。因此，以经济代价最小为目标得出的切负荷策略更符合电网切负荷要求。

4.3 秒级／分钟级负荷切除算例

经毫秒级负荷切除优化得到负荷切除方案后，切除方案中各负荷用户下分路开关，更新用户信息表，进行第2 轮秒级／分钟级负荷切除。MOPSO 算法的相关参数设置如附录B表B2所示。

设置切除量为250 MW，为了更好地体现负荷用户间博弈的多样性，γmax取5，即所得出的切除策略允许有±5%的浮动区间，对优化解集中的8 种优化结果进行比较，8 种优化结果的对比指标包括总经济代价、总切除量和切负荷精确度。

对3项指标进行标准化处理，8种优化结果的各项指标对比如图4 所示，图中指标为标幺值，其具体有名值如表3所示。

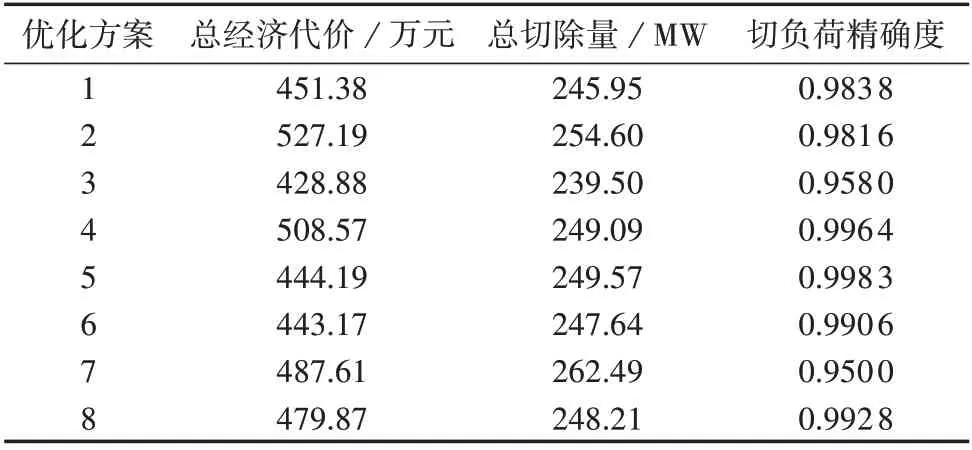
表3 秒级／分钟级负荷切除博弈结果Table 3 Game results of second／minute load shedding

图4 优化方案的各项指标对比Fig.4 Comparison of indicators among optimization schemes

通过比较得出的博弈结果，根据电网对于秒级／分钟级负荷控制的要求不同，选择不同的切除方案。当电网未给出偏向要求时，综合3 项指标，选择方案6作为本次秒级／分钟级负荷控制的最终方案。

经测试，MOPSO 算法的求解时间为15.3 s，可以满足FC-Ⅱ段中频率控制问题的计算时间需求。

4.4 轮次切除影响分析

在整个轮次切负荷方案中，共有16 个负荷用户参与了第1 轮的毫秒级负荷切除优化。定义负荷切除率为负荷用户l的切除量与该用户总可切量的比值，如式（23）、（24）所示。

式中：λl和ηl分别为负荷用户l的第1、2 轮负荷切除率；ΔP″i为负荷用户l的第2轮切除量。

图5比较了16个负荷用户的不满意度与其在第1、2轮的负荷切除率之间的关系，表4给出了具体数据。从图5、表4中可以得到以下结论。

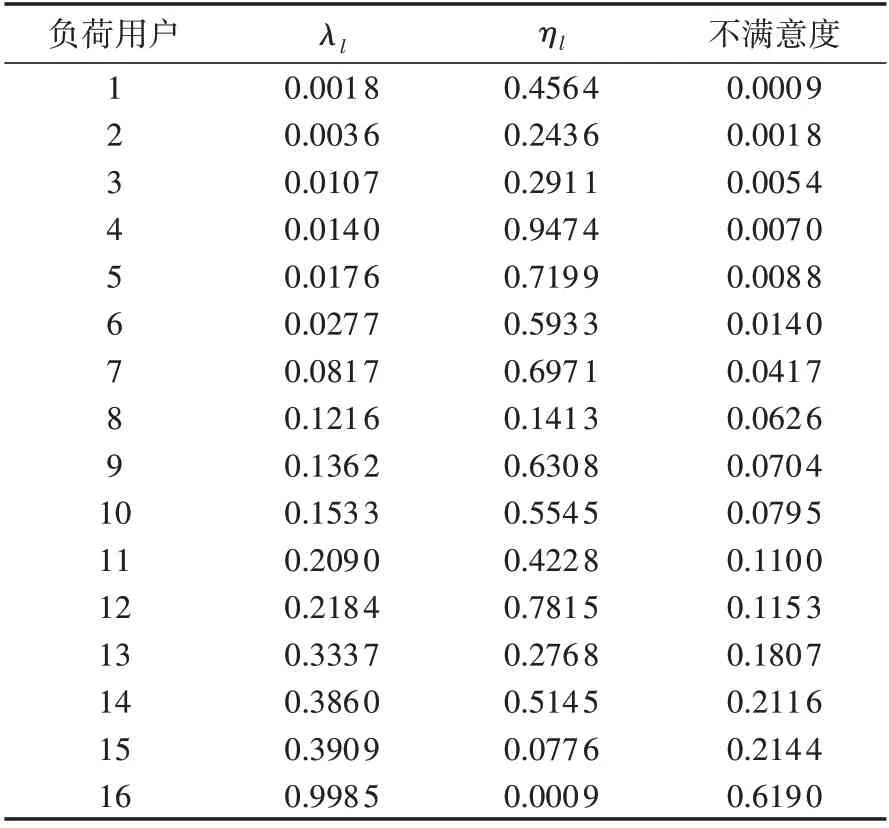
表4 负荷用户不满意度与负荷切除率的具体数据Table 4 Specific data of load user dissatisfaction and load shedding rate

图5 负荷用户的不满意度与其第1、2轮负荷切除率之间的关系Fig.5 Relationship between dissatisfaction degree of load users and load shedding rate in first and second load shedding rounds

1）总体而言，在第1 轮毫秒级负荷切除优化中切除率越高的负荷用户，其不满意度越高。

2）总体而言，负荷用户的不满意度越高，则其参与第2 轮负荷切除的切除率越低，符合各负荷用户之间的博弈策略。

3）少数负荷用户出现了切除率与不满意度不匹配的情况，如负荷用户8、12、14。这是因为第2轮负荷切除策略除了计及不满意度外，还考虑了负荷重要程度约束以及切负荷精确度约束等。以负荷用户8 为例，虽然其不满意度较低，但重要程度较高（算例中其各个分路开关的等级为级别1—3），因此在第2轮的负荷切除率较低。

5 结论

本文提出了频率安全分段控制下，用户侧毫秒级负荷控制（FC-Ⅰ段）和秒级／分钟级负荷控制（FC-Ⅱ段）的轮次切负荷优化策略。在FC-Ⅰ段，以经济性最优为目标，基于McCormick 松弛和内点法，快速求解毫秒级负荷切除策略；在FC-Ⅱ段，综合考虑FC-Ⅰ段后的剩余可控量与用户的参与意愿，建立多用户非合作博弈模型，获得秒级／分钟级负荷切除方案。算例结果表明，所提的毫秒级负荷切除优化策略可以在经济性最优的前提下保证频率控制效果；所提的秒级／分钟级负荷优化策略在保证经济性计及了毫秒级负荷切除的影响，得到的负荷切除方案合理有效。

需要说明的是，本文在研究过程中未考虑负荷切除时配电网的潮流约束。随着配电网内分布式电源等的不断增多，用户的负荷切除对配电网的影响（如分布式电源脱网等）也逐渐增大。因此，后续拟进一步计及配电网潮流约束、分布式电源安全约束等开展研究工作。

附录见本刊网络版（http：//www.epae.cn）。