关联代数上的非线性Lie中心化子

周斯名

(吉林师范大学数学学院, 吉林长春,130000)

同构、导子和中心化子是环和代数上的重要映射, 是研究环和代数的一种重要工具。关于中心化子及其等价形式的研究一直深受研究人员的关注, 很多学者通过恒等式变换及代数组合的方法研究中心化子。设φ是2-扭自由半素环R上的可加映射, 若对于任意的A∈R都满足2φ(A2)=Aφ(A)+φ(A)A, 文献[1]证明了φ是中心化子; 对于任意环R, 以及线性映射φ:R→R, 如果满足对任意的x,y∈R,都有φ(xyx)=xφ(y)x, 文献[2]证明了φ是中心化子。设φ是标准算子代数R的可加映射, 若φ满足φ(Am+n+1)=Amφ(A)An(其中m、n为正整数), 文献[3]证明了使得对于任意的a∈R有φ(a)=λa。设X为实或复域F上的Banach 空间,R为X上的标准算子代数,I是R的单位元。设R是一个作用在Banach 空间χ上的含单位元I的标准算子代数,φ:R→B(X)是一个可加映射。如果存在正整数m,n,r,使得(m+n)·φ(Ar+1)-mφ(A)Ar-nAr φ(A)∈FI对任意的A∈R成立, 文献[4]证明了存在λ∈F, 使得对于任意A∈R有φ(A)=λA。设(X, ≤)是一个有限预序集,R是含单位元的2-扭自由的交换环。I(X,R)是定义在R上是关于X的关联代数, 如果X由有限个连通分量组成, 文献[5]证明了X的每一个李三导数都是标准的。设(X, ≤)是一个有限预序集,R是含单位元的2-扭自由的交换环。I(X,R)是定义在R上是关于X的关联代数, 文献[6]证明了导子I(X,R)的每一个Jordan 导子是导子。设(X, ≤)是一个有限预序集,R是含单位元的2-扭自由的交换环。I(X,R)是定义在R上是关于X的关联代数, 文献[7]证明了I(X,R)上的任意一个李导子都是标准的。

弱化映射条件一直是许多学者研究的热点, 设M是实或复数域F上的Hilbert 空间上的一个因子von Neumannn 代数, 对于任意非零整数m、n且满足(m+n)(m-n) ≠ 0, 文献[8]证明了M上满足2mφ(AB)+2nφ(BA)=mφ(A)B+nφ(B)A+mAφ(B)+n Bφ(A)的非线性映射φ为可加中心化子。设R是广义矩阵代数, 若φ:R→R是非线性Lie 中心化子,φ:R→R是可加的中心化子,τ:R→Z(R)对所有x,y∈R, 满足τ[x,y] = 0, 在一些微弱的假设下, 文献[9]证明了φ=φ+τ。设U是一个(m+n)(m-n) ≠ 0-无挠的三角代数且满足πA(Z(U))=Z(A)和πB(Z(U))=Z(B), 对于固定整数m,n且(m+n)(m-n) ≠ 0, 若L是U上的一个非线性(m+n)-Lie 中心化子, 则存在一个中心元λ和一个到U的中心且在交换子上为0 的映射ξ使得文献[10]证明了对任意的x∈U, 有L(x)=λ x+ξ(x)。上述文章均停留在非线性Lie 中心化子与其他映射的联系层面, 没有真正分析非线性Lie 中心化子的具体形式和内在性质。基于此, 本文研究非线性映射下的中心化子及Lie 中心化子, 利用代数结合的方法研究算子理论, 并在此基础上探究了关联代数上的非线性中心化子及非线性Lie 中心化子的性质, 对于关联代数上非线性映射的相关结论有重要意义。

1 预备知识

定义1[9]设R是环或代数。如果一个线性(非线性)映射φ:R→R满足对任意A,B∈R有φ(AB)=φ(A)B(φ(AB)=Aφ(B)), 则称φ是左(右)中心化子; 若φ既是左中心化子又是右中心化子, 称φ是(非线性)中心化子。

定义2[9]设R是环或代数。如果一个线性(非线性)映射φ:R→R满足对任意A,B∈R有φ([A,B])=[φ(A),B] =[A,φ(B)], 则称φ是Lie(非线性)中心化子。

关联代数的概念最早由Ward[11]引出, 之后人们对关联代数上的映射进行了研究。

定义3[12]若集合X中的二元关系" ≤ "满足以下两个条件:(1)∀x∈X有x≤x;(2)∀x,y,z∈X,若有x≤y和y≤z⇒x≤z, 则称X是一个预序集, 记作(X, ≤)。

定义4[12]取预序集X中的任意两个元素x,z, 区间[x,z]定义为{y∈X x≤y≤z}。若预序集X中的所有区间都是有限的, 则称X是局部有限预序集。

引理1若δ[12]满足δ(x,y)=δxy,x≤y其中δxy∈{0, 1}是Kronecker 符号, 则δ是关联代数I(X,R)中的单位元。

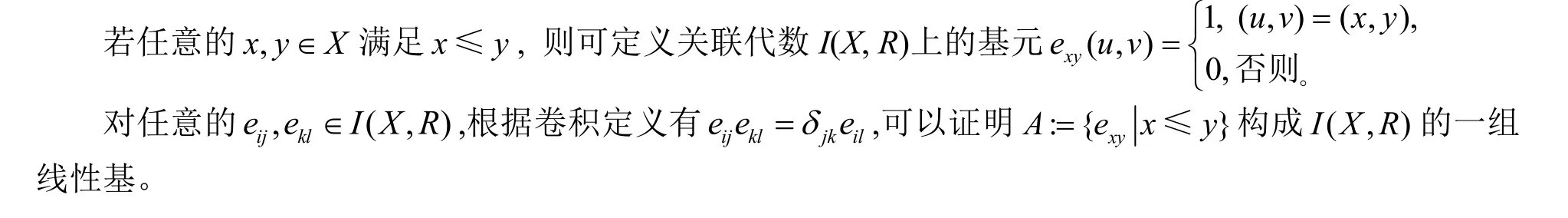
2 主要定理及证明

定理1 设(X, ≤)是一个有限预序集,R是含单位元的2-扭自由的交换环。I(X,R)是定义在R上是关于X的关联代数, 设φ是关联代数I(X,R)上的非线性映射φ:I(X,R)→I(X,R), 若φ为中心化子,则φ为可加中心化子。

对于基元ei j,ekl∈A, 其中i,j,k,l∈X且互不相等, 有如下情况: (1)φ(α+α)=φ(α)+φ(α); (2)φ(α+β)=φ(α)+φ(β),其中α≠β。