多目标空间探测智能轨迹优化方法综述*

李海洋 周晓东 张旭光 宝音贺西

(1.上海卫星工程研究所，上海 201109) (2.上海航天技术研究院，上海 201109) (3.清华大学 航天航空学院，北京 100084)

引言

探索浩瀚宇宙是人类自古以来的梦想.随着技术的进步，太空进入门槛降低，航天将有望迎来一段黄金时期，人类需要更加经济、理性且可持续的太空探索与开发方案——多目标空间探测即为一种可选方案.多目标空间探测是指用一个或多个航天器对多个空间目标进行探测，其优势在于能够以较低的花费获取极大的收益，其难点在于任务的设计与优化.深空探测任务设计中，部分任务需要借用行星进行引力辅助，或者在探测器完成其主要任务的前提下顺便对其他天体进行飞越，这些都属于一个航天器访问多个目标的情况.表1是根据NASA统计的1958-2016年的深空探测任务[1]而整理得到的访问多个目标的深空探测任务，这些任务均给人类带来极大的科学收益.但是多目标空间探测任务与上述深空探测任务并不完全相同.上述深空探测任务以某一目标或少量目标为主要目标，其他目标的探测是通过借用其进行引力辅助或者在访问主要目标的基础上附加进行的.多目标空间探测与之不同之处主要有几点：一是多目标空间探测并不存在主要目标，目标的选择是为了任务整体收益的最大化；二是多目标空间探测的目标更多，可多达几十个；三是多目标空间探测并不仅限于深空探测任务，地球轨道同样有多目标空间探测的任务需求.因此能够创造更大的收益.

表1 访问多个目标的深空探测任务(按发射日期排序)Table 1 Space missions that visited multiple targets (sorted by launch date)

多目标空间探测从任务目标类型上可分为深空任务和地球轨道任务.深空多目标任务方面，探测目标主要为大行星及小天体(小行星和彗星)，其中小天体为重点[2].小天体被认为保留着太阳系早期物质，对于研究太阳系起源以及生命起源有着极其重要的科学价值；一些小天体上含有储量丰富的稀有金属，小天体采矿也有望形成一个新兴产业；同时，一些小天体有着潜在的撞击地球威胁，对小天体进行防御也是非常重要研究内容.地球轨道多目标任务方面，由于人类进入太空的能力已经较为成熟，更加高效地对空间进行开发利用将会是未来的重点，空间碎片清除、在轨燃料加注、在轨维修等方面对多目标空间探测均有重大需求.此外，多目标空间探测还可以是多个航天器协同进行，每个航天器对多个目标进行探测；多目标空间探测的目标并不局限于天体或者航天器，只要有探测价值均可视为目标.

虽然多目标空间探测有着诸多优点，但也有许多困难，其中最为主要的困难之一为轨迹优化，又分为转移轨迹优化和探测序列优化两部分.以多目标主带小行星探测为例，目前已经编号的主带小行星共计约12万颗，假设筛除掉轨道偏心率较大、轨道倾角较大、以及绝对星等较大的小行星后，还剩下3000颗备选小行星.若考虑单个航天器访问10颗小行星的多目标任务，每次访问完一颗小行星后经过筛选，下一个可选目标为1000个，其可选的探测序列组合为3×1012个.为了从这些组合中选出最优的探测序列，若采用穷举法对所有的探测序列都进行一次评估，假设每次评估耗时1ms，则评估完所有探测序列的时间约为95年(不考虑使用并行计算等其他方法).通过这一简单直观的比较可见多目标空间探测任务设计之复杂，设计空间之巨大，优化之难.因此，全局优化，包含快速准确的转移轨迹评估方法与高效的探测序列全局优化方法，是多目标空间探测轨迹优化的核心难点.

此外，未来航天任务对航天器的自主性能需求越来越高，对星上实时规划、自主决策等方面有要求[3]，多目标空间探测任务同样如此.面对未来可能会存在大量航天器同时进行多目标空间探测任务的情况(如SpaceX的星链计划)，近地卫星多航天器多目标协同自主工作将成为新模式，深空探测器由于器地时延更需要具备器上自主优化的能力.此外，多目标探测任务中航天器自主优化能力的提升也能大大降低地面飞控系统的负担与压力.在多目标空间探测任务中，需要能够实时对转移轨迹和探测序列进行优化.但是航天器星上计算能力非常有限，任务设计时常用的优化方法无法在航天器上执行，因此与航天器星上计算能力相适应的实时优化也是多目标空间探测轨迹优化的重要挑战.

面对上述难点与挑战，智能方法有望提供解决途径.智能方法在航天动力学领域一直有着广泛应用[4].航天动力学领域应用人工智能技术应以需求为导向，从需求出发.作为航天动力学的研究内容之一，多目标空间探测轨迹优化对智能方法的需求与其难点与挑战是对应的.多目标空间探测轨迹优化的全局优化难度很大，需要解决转移轨迹快速评估和探测序列全局优化的问题，而智能方法在快速准确预测与求解组合优化问题上有着优异的表现.同时，面向未来航天任务的多目标空间探测轨迹优化需要具备实时优化的能力，需要解决转移轨迹实时优化和探测序列实时优化的问题，而实时优化也正是智能方法的研究重点之一.人工智能中常用的方法有树搜索、进化计算以及机器学习，这三种方法也是航天动力学领域应用最多的智能方法[4].

多目标空间探测轨迹优化近十几年来已逐渐成为轨道动力学与控制领域的研究热点，国际空间轨道设计竞赛(Global Trajectory Optimization Competition, GTOC)和中国空间轨道设计竞赛(China Trajectory Optimization Competition, CTOC)在其中起到了重要推动作用.本文首先通过国内外轨道竞赛介绍多目标空间探测轨迹优化的研究趋势，然后从转移轨迹优化和探测序列优化两个方面对其中涉及智能方法的研究进行综述，其中，转移轨迹优化将分为进化计算方法和机器学习方法两个部分进行综述.

1 多目标空间探测轨迹优化国际研究趋势

多目标空间探测轨迹优化的研究，以国际空间轨道设计竞赛GTOC和中国空间轨道设计竞赛CTOC为代表.两个竞赛所研究的问题均为极具挑战、几乎不可能得到全局最优解的问题，其中绝大多数问题是多目标空间探测轨迹优化问题.此外，国内外高水平的研究团队都会参加竞赛，因此可以通过梳理竞赛来窥探多目标轨迹优化国际研究趋势.

GTOC由欧洲空间局先进概念组的Dario Izzo博士在2005年发起，每一年或两年举办一次，至今(2020年)已经举办了10届，每届的冠军负责举办下一届竞赛.参与过该项赛事的团队共有134个，除首届外其他均为多目标空间探测问题.综合各届竞赛题目来看，多目标空间探测的探测目标主要为小行星(近地小行星和主带小行星)、木卫系统、宇宙射线源和空间碎片；任务形式有单个探测器飞越或者交会、多个探测器协同探测等形式.

从参与团队来看，在GTOC中起主导地位的为美国喷气推进实验室(Jet Propulsion Laboratory, JPL)和欧洲空间局先进概念组(European Space Agency′s Advanced Concepts Team, ESA-ACT).JPL获得第一名的次数遥遥领先.JPL主导或参与了美国的多项深空探测任务，包括表1中提到的先锋号系列、水手号系列、旅行者号、伽利略号、卡西尼号、深空1号、星尘号、深度撞击号和黎明号，几乎包含了所有表1中提到的美国任务，可以认为JPL无论在科研还是工程上都处于国际领先地位.ESA-ACT虽然仅获得过一次冠军，但是其成绩始终稳定靠前，综合实力并不逊于JPL，作为竞赛的发起方始终走在多目标空间探测轨迹优化研究的最前线.此外，还有美国国家航空航天局多家研究中心(约翰逊研究中心，戈达德研究中心等)、法国国家太空中心、德国宇航局、俄罗斯赫鲁尼契夫国家航天研制中心等多家航天机构，都灵理工大学、格拉斯哥大学、米兰理工大学、莫斯科大学、奥斯汀大学等多家欧美航天强校持续参与到竞赛中来并取得不错的成绩，充分说明多目标空间探测在科研和工程上均是极具挑战的研究内容，一个团队需要在科研和工程上都具备扎实的基础才可以取得优异的成绩.

中国研究团队包括清华大学、北京航空航天大学、南京航空航天大学、中科院、国防科技大学、西安卫星测控中心、北京飞控中心、南京大学、西北工业大学、哈尔滨工业大学等(按参赛时间排序)同样积极参与到GTOC中来，并且成绩整体上在不断进步，在第十届竞赛中首次包揽了前两名，力压欧美其他传统强队.图1总结了各国各次竞赛的参赛成绩，横坐标为竞赛的届次，纵坐标为该国在该次竞赛中的分数.分数的计算方法为：该国所有参赛并提交正确结果的团队里，第1名得16分，第2名得8分，第3名得4分，第4名得2分，其余得1分；这样的计分方式，既能体现该国研究团队的整体实力，又能体现该国的参与程度.从图中可以看出，随着竞赛举办次数的增加，中国研究团队在不断缩小与欧美研究团队的差距，且在第十届竞赛中成为第一；美国在JPL参赛的大多数届次中仍然保持领先地位；欧洲中国研究团队的冲击分数而受到影响；俄罗斯分数在逐渐下降，这与其参与程度有一定关系；在美国、中国、欧洲、俄罗斯这四个航天大国中，中国有着非常强劲的势头，这也表明在多目标空间探测轨迹优化领域中国的研究团队紧跟着中国从航天大国迈向航天强国的步伐.

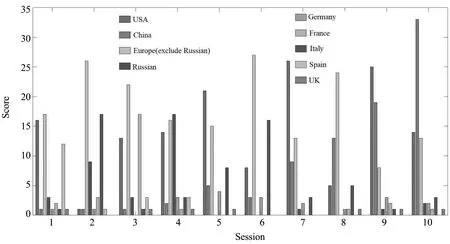
图1 国际轨迹优化竞赛各国参赛成绩Fig.1 Scores of global trajectory optimization competition of various nations

我国的研究团队能在GTOC中取得如此优异的成绩，与我国自己的CTOC是分不开的.CTOC由清华大学在2009年发起，至今(2020年)已经举办了十届，也已经有文献对其进行了总结与回顾[5,6]，本文不再赘述.CTOC题目绝大多数也为多目标空间探测轨迹优化问题，包括小行星探测、小行星表面巡游、空间碎片清除、多星编队、木星磁场与木卫探测等.参赛团队也主要为上述参与过国际轨迹优化竞赛的团队.每一次的GTOC与CTOC不仅锻炼了我国的研究团队，也一次次地为多目标空间探测任务提供新的思路，为将来我国开展多目标空间探测任务打下了夯实的基础.

综合各研究团队在竞赛中的求解方法来看，智能方法越来越多地被应用，而且取得的成绩也越来越好[5].最近的两届GTOC中排名前三的团队均采用了智能方法[7-9]，可见智能方法在多目标空间探测轨迹优化中将会越来越重要.

接下来，本文分别从转移轨迹优化和探测序列优化两部分的智能方法进行综述.

2 转移轨迹优化进化计算方法

转移轨迹的形式一般为脉冲、连续推力、引力辅助(可以视为一种变轨形式)等.考虑到航天器所携带燃料有限且昂贵、任务时长有限等因素的制约，转移轨迹设计的核心问题即为优化问题，优化目标通常为燃料消耗或者任务时长.转移轨迹优化问题为复杂的优化问题，存在着许多局部最优解.由于该类问题中许多优化变量的梯度并不容易解析获得或者不连续，基于梯度的优化方法解决该类问题有着诸多困难，比如对初值的要求较高，或者不易跳出较差的局部解.进化计算，如遗传算法，差分进化，粒子群优化等，不需要优化变量的梯度，且全局性较好，因此被广泛应用到转移轨迹优化中.

2.1 脉冲轨迹优化

Cage等[10]最早在1994年将遗传算法应用到深空脉冲轨迹优化中，并且指出遗传算法明显优于当时通用的网格搜索算法.此后，Kim和Spencer[11]用遗传算法研究了脉冲交会问题，并用霍曼转移与双椭圆转移验证了遗传算法的最优性.Abdelkhalik 和Mortari[12]改进了Kim论文中的求解模型，用遗传算法计算了其中的算例并得到了更优的结果.Vasile等将分支技术应用在进化算法中提出了进化分支算法，研究了地火转移多脉冲轨迹优化问题[13]，也提出了一种基于行为的元启发算法应用到地球小行星的双脉冲转移轨迹优化中[14].Radice和Olmo[15]用蚁群算法研究了双脉冲转移问题，不仅得到了之前研究中的最优解，还发现了若干新的局部解.罗亚中[16]使用遗传算法、并行模拟退火单纯形等方法研究了空间最优交会问题.Zhang等用遗传算法研究了复杂约束条件下的交会问题[17]以及多目标优化问题[18].Yao等[19]提出了一种自适应差分进化算法研究了脉冲问题.Sentinella和Casalino[20]将差分进化、遗传算法与粒子群优化并行计算优化多脉冲问题.Pontani 等[21]用粒子群优化研究了多脉冲交会问题，并建议对于交会问题可以首先尝试使用粒子群优化.Bessette和Spencer[22]研究了用差分进化、粒子群优化以及进化策略优化多脉冲转移并进行比较，发现粒子群优化效果更好.可以将进化计算方法的全局最优性与非线性规划等基于梯度算法的局部最优性结合起来，使用进化计算为非线性规划算法提供初值，能够高效求解脉冲转移轨迹优化问题.

2.2 小推力轨迹优化

小推力轨迹优化领域智能方法同样有着较多的应用.Rauwolf和Coverstone-Carroll[23]在1996年使用遗传算法优化了深空小推力轨迹，文中将小推力轨迹分成多段，每段内推力方向为固定值，优化每段开关机以及推力方向角.除了将小推力轨迹进行分段，还可以将推力方向角用函数进行描述，从而优化函数的参数.Dewell和Menon[24]将推力方向角表示为切比雪夫多项式的形式，用遗传算法优化切比雪夫多项式的系数，研究了地球同步轨道小推力转移问题.Wall和Conway[25]将小推力方向角用三次多项式拟合，用遗传算法优化三次多项式系数.Ghosh和Conway[26]用B样条曲线拟合小推力方向角，用粒子群优化对B样条曲线系数进行优化.Lee等[27]使用李雅普诺夫Q函数进行小推力轨迹优化，用遗传算法优化Q函数的参数，研究了同时考虑燃料消耗与飞行时间的多目标优化问题.上述进化计算方法都是将小推力问题进行了一定的近似(比如将推力方向角用含参数的函数描述)，对于末端精度要求不高或者对最优性要求不高的情况下适用.

除了直接优化小推力开关机与方向角之外，还有许多学者使用智能方法为其他数值解法提供初值.Coverstone-Carroll等[28]用遗传算法优化协态变量与转移时间，为SEPTOP(美国喷气推进实验室开发的小推力求解软件)提供初值，研究了同时考虑燃料消耗与转移时间的多目标优化问题.Wuerl等[29]、Sentinella和Casalino[30]也研究了使用遗传算法为小推力间接法求解提供初值.Pontani和Conway[31]研究了粒子群优化在脉冲以及小推力轨迹优化中的应用，应用之一即为小推力间接法求解提供初值.同样，Jiang等[32]也使用粒子群优化为小推力间接法求解提供初值.Shan和Ren[33]使用粒子群优化提供协态初值，再将轨迹离散后作为初值用直接法进行求解.Chilan和Conway[34,35]将脉冲、连续推力段和滑行段整体进行优化，机动类型也作为优化的结果，使用遗传算法为非线性规划提供初值.可以看到进化计算方法在小推力轨迹优化初值求解中有着较多应用，能够充分发挥进化计算方法全局性好的优势.

2.3 引力辅助轨迹优化

多次引力辅助的轨迹较为复杂，如图 2所示，其优化也有着许多研究.对于给定的引力辅助序列，如何选取引力辅助时刻以及如何施加深空机动是一个较为复杂的优化问题，许多学者使用智能方法进行优化.Vasile等设计了进化算法与分支策略结合的进化分支算法，研究了脉冲和小推力的含深空机动的多引力辅助轨迹优化问题[36]，又提出了多主体协作搜索算法[37]，并对该算法进行了改进研究多目标优化问题[38].Vasile等[39]还改进了差分进化算法，在含深空机动的多引力辅助问题上其性能优于标准的差分进化算法.Olds等[40]和Qiao等[41]使用差分进化算法研究了含深空机动的多引力辅助轨迹优化问题，发现算法的性能对算法参数设置非常敏感.Izzo等[42]在研究木卫探测的问题时将参数自适应、约束处理等技术应用在进化算法上，避免了人工设置算法参数.Izzo等[43]还提出了空间剪枝方法研究多引力辅助问题，与差分进化、遗传算法、粒子群优化结合，提升了算法性能，Vasile等[44]在此基础上研究了含深空机动的多引力辅助问题.Schütze等[45]用空间剪枝研究了小推力引力辅助多目标优化.Schütze等[46]使用非支配排序遗传算法NSGA-II对引力辅助轨迹多目标优化进行了研究，同时NSGA-II的提出者Deb等[47]也用该算法研究了类似问题.

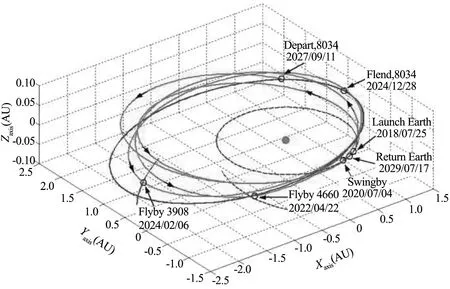
图2 多引力辅助探测轨迹(图片来自文献[41])Fig.2 Trajectory of multiple gravity-assist mission

与小推力轨迹优化问题类似，引力辅助轨迹优化中也有学者使用智能方法为其他数值解法提供初值.Crain等[48]将遗传算法得到的结果作为初值，使用递归二次规划来进一步优化.Woo等[49]使用遗传算法为SEPTOP提供初值，研究了小推力引力辅助轨迹优化问题.Yang等[50]使用粒子群优化为含引力辅助的小推力间接法求解提供初值.此外，乔栋等[51,52]用差分进化为序列二次规划提供初值，研究了使用引力辅助的小行星探测轨迹优化问题.这些研究也再一次表明进化计算方法在提供优化初值上的优势.

由于含深空机动的多引力辅助轨迹优化问题的复杂性，许多学者以该问题为基础将多种智能方法进行比较.Myatt等[53]比较了遗传算法、差分进化、粒子群、交叉熵等多种算法，发现差分进化性能更优.Bessette和Spencer[54]比较差分进化和粒子群优化，认为粒子群优化性能更好，虽然二者均能找到最优解，但是粒子群优化需要的迭代次数更少.Sentinella和Casalino[55]将差分进化、遗传算法与粒子群算法并行计算，每次迭代时三种算法共享最优个体，在某些复杂问题上性能更好.Vasile[56]等比较了差分进化、遗传算法、粒子群优化等，认为各种算法的性能非常依赖于研究问题本身.

3 转移轨迹优化机器学习方法

机器学习在转移轨迹优化中的应用主要有两个方面，一是对转移轨迹优化最优指标(如最优的燃料消耗或者转移时间)的快速预测，二是设计实时最优控制器.

3.1 最优指标快速预测

由于多目标空间探测轨迹优化需要大量优化转移轨迹，如果可以快速准确地对转移轨迹的最优指标进行预测，避免精确优化求解，将会极大地提高计算速度.该问题可以概括为：已知初始轨道和末端轨道，如何做到不进行精确优化而快速准确地给出最优燃料消耗或者最优转移时间？该问题对小推力转移尤其重要，因为小推力轨迹的优化过程较为耗时.Edelbaum[57]早在1961年就研究过航天器轨道转移所需要的最优速度增量，给出了用初末轨道状态差表示的速度增量表达式.但是Edelbaum所研究的轨道转移是多圈转移，其速度增量公式推导是以一个轨道周期为基本单位，将不足整数圈的部分忽略.但是在深空探测任务中，圈数非常多的小推力转移是不现实的，更接近实际情况的是非整数圈转移.针对该问题，Casalino[58]基于Edelbaum的方法研究了共面小偏心率轨道转移的最优速度增量估计公式，Gatto[59]又在其基础上进一步研究了非共面轨道转移的情况.在他们的方法中，最优速度增量需要通过求解方程得到，而且对于交会问题还需要添加较为复杂的修正项.机器学习由于其处理数据关联上的优势，对于该问题非常适用.Hennes等[60]以及Mereta等[61]使用机器学习方法预测燃料最优小推力问题的剩余质量，使用了多种机器学习方法比如回归森林和决策树等，预测精度远优于双脉冲近似.对于脉冲转移问题，Shang等[62,63]使用高斯过程回归方法预测地球到主带小行星转移的最优速度增量，同样是为了解决大量计算下精确优化速度太慢的问题.Zhu[64,65]以及Li[66]等使用深度神经网络预测小推力时间最优问题、小推力燃料最优问题以及多脉冲速度增量最优问题，预测精度高达99%.此外，机器学习还可以用在进化计算优化转移轨迹的过程中，用来预测目标函数[67]或者提供初值[68].

3.2 实时最优控制

实时最优控制也是轨迹优化的一个重要领域，近年来随着神经网络相关研究的进展，轨迹优化领域基于神经网络的实时最优控制也有着较多研究，一般通过大量的数据训练来进行，如图3所示.Sánchez等[69]针对着陆问题系统地研究了基于神经网络的实时最优控制.在他们的研究中，首先需要通过优化生成大量的状态-控制对数据，然后使用生成的数据训练神经网络，训练完成后，每当给神经网络一个当前的状态，神经网络都应当给出接近最优的控制律.为了提高神经网络控制深空小推力轨迹的末端精度.Cheng等[70]设计了两个神经网络分别进行大范围转移段控制和末端精确控制.此外，对于小天体着陆问题，Cheng等训练了神经网络学习小天体的不规则引力场并进行了小天体着陆控制[71,72]，还训练了神经网络学习小天体着陆轨迹间接法的协态初值[73].Furfaro等[74]使用循环神经网络设计着陆控制器.上述神经网络控制的输入为位置速度等状态信息，但是在实际情况中精确的位置速度可能不易获得，Furfaro等[75]设计了直接输入着陆图像的神经网络控制器，使用卷积神经网络以及循环神经网络处理序列的图像信息从而给出最优控制律.

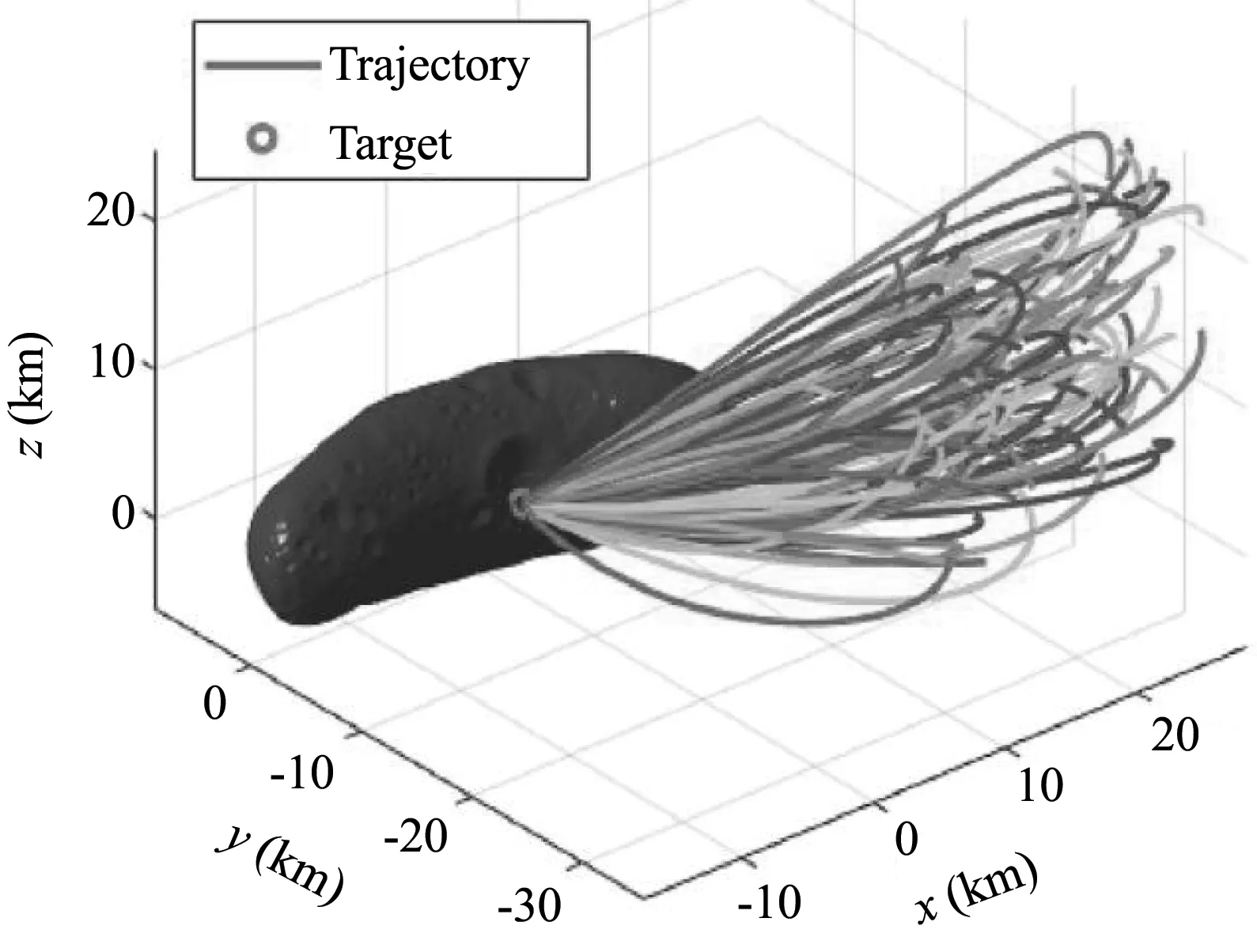
图3 小行星着陆神经网络控制轨迹[76]Fig.3 Asteroid landing trajectories using neural network control

强化学习方法在转移轨迹优化领域也有应用.Dachwald[76]在2004年就使用强化学习进行了太阳帆轨迹优化，用遗传算法训练单层神经网络作为最优控制器.Dachwald使用强化学习的目的是为了避免优化陷入局部最优解，从而找到全局最优解[77].在实时控制方面，Gaudet和Furfaro[78]使用强化学习训练了小天体附近悬停控制器，Willis等[79]又在此基础上将精度提高了一个量级.针对着陆问题，Gaudet等[80]使用强化学习训练了六自由度的神经网络控制器，Cheng等[81]使用强化学习训练神经网络预测着陆轨迹间接法的协态初值.

机器学习方法本质是对数据的处理，因而该方法在处理最优指标预测等方面可以获得大量数据的问题上具有明显优势，但是对于航天中面临的更多未知、小样本的新问题如何应用，仍是值得深入研究的内容.

4 探测序列优化智能方法

探测序列优化是多目标空间探测轨迹优化的核心问题，也是GTOC中最为常见的问题，如图4中的木卫巡游探测任务.探测序列优化是一个组合优化问题，若考虑时间因素则为离散-连续变量的组合优化问题，离散变量为目标的选取以及排序等，连续变量为与目标飞越或者交会的时刻等.由于解空间巨大，探测序列优化是一个极其复杂的优化问题，研究中多用智能方法进行优化.探测序列优化主要包含多引力辅助序列优化，多目标小天体探测序列优化，以及多目标在轨服务与空间碎片清除序列优化.

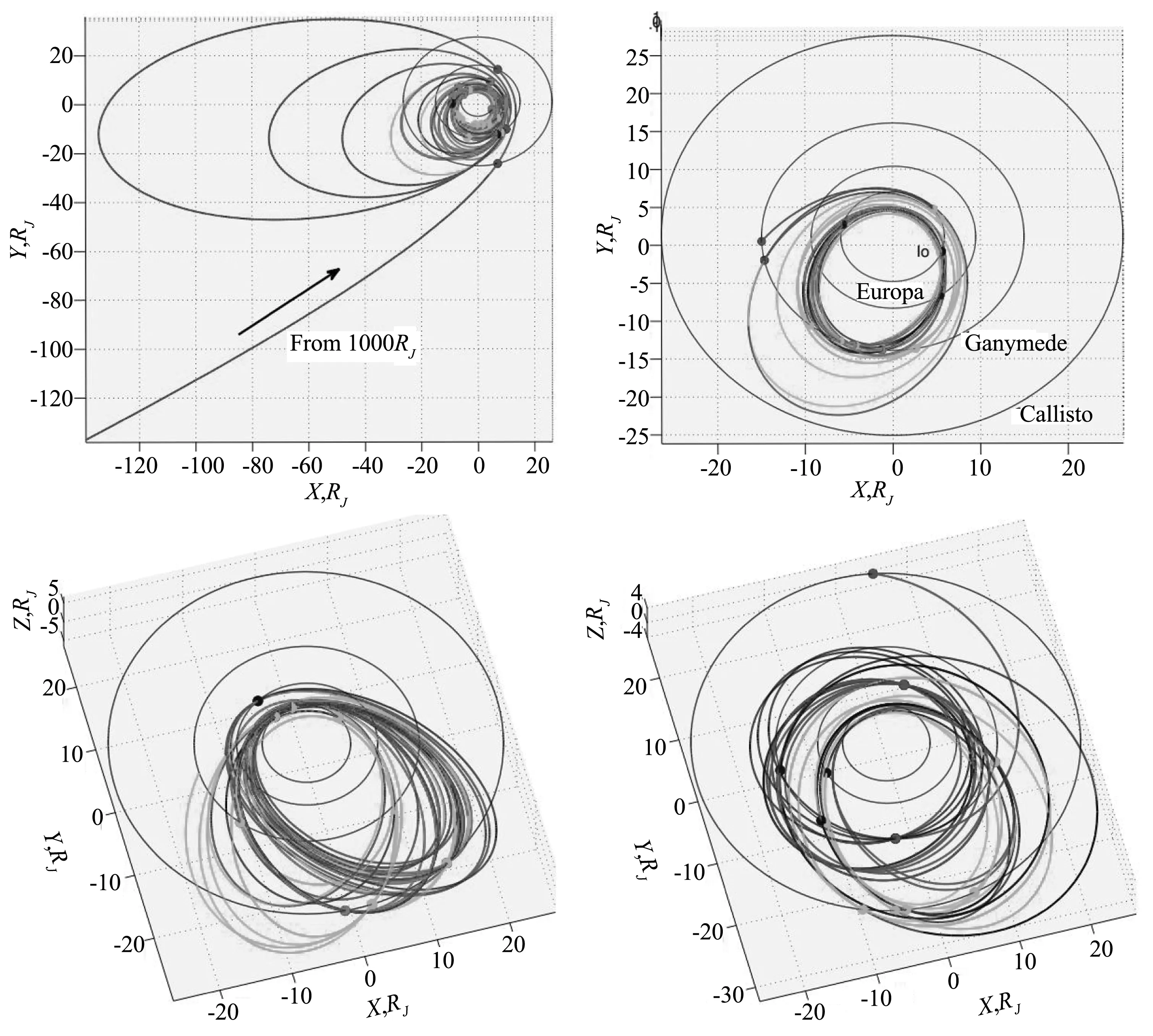
图4 木卫巡游探测任务[94]Fig.4 Jovian moons tour

4.1 引力辅助序列优化

多引力辅助序列优化与1.2.3小节中关于多引力辅助问题的研究不同，这里引力辅助的序列也变为了待优化的离散变量，与引力辅助时刻等构成了离散-连续变量的组合优化问题.华鹏[82]使用粒子群算法确定行星序列，再用遗传算法求解小推力轨道.Ceriotti和Vasile[83]提出了一种基于蚁群算法的多引力辅助序列优化算法，并与遗传算法进行了比较.之后，Vasile等[84]又提出了一种新的生物启发式算法——绒泡菌优化算法，进行了多引力辅助序列优化，仿真表明该算法只需进行少量的参数调试即可得到优异的性能.Gad和Abdelkhalik[85]针对引力辅助次数无法提前确定的问题，提出了隐藏基因遗传算法，将引力辅助次数也变为优化的结果，后来又将隐藏基因遗传算法进行了改进[86].之后，二人又提出了可变种群大小的遗传算法研究了类似的问题[87]，算法性能得到进一步提升.Englander等[88]使用遗传算法优化外层序列，使用粒子群结合差分进化优化内层连续变量，通过在遗传算法中使用空值的办法优化引力辅助次数.Englander等[89]继续使用遗传算法优化外层序列的同时，在内层使用盆地跳法优化小推力转移问题.此外，Izzo等[90]使用了一种集束搜索的懒人树搜索算法(Lazy-Race Tree Search)研究了木卫系统探测问题.Hennes和Izzo[91]使用蒙特卡洛树搜索重现了卡西尼任务，得到了原任务一样的引力辅助序列和非常接近的时间线.

4.2 小天体探测序列优化

4.3 在轨服务与空间碎片清除序列优化

多目标在轨服务与空间碎片清除序列优化问题也有着较多研究.与小天体探测相比，在轨服务与空间碎片清除会更多地考虑目标全部访问的问题.树搜索方法方面，相关研究主要有Barbee等[108]使用的级数搜索算法、Madakat等[109]使用的分支定界方法、Olympio和Frouvelle[110]使用的分支和剪枝策略，以及Bérend和Olive[111]使用的多优化指标的分支定界算法等.由于在轨服务与空间碎片清除序列优化问题与旅行商问题具有较高的相似度，因此在旅行商问题上表现优异的进化计算类方法同样适用于在轨服务与空间碎片清除问题.模拟退火算法[112,113]、遗传算法[114,115]、倒置算子的遗传算法[116]、混合编码遗传算法[117]、多目标遗传算法[118]、多目标粒子群算法[119]等都被用来研究在轨服务与空间碎片清除序列优化问题.还有学者提出了改进的进化计算类方法，如多主体协作搜索算法[120]以及绒泡菌优化算法[121]等.蚁群算法在该问题中也有较多应用.Stuart[122]使用蚁群算法，优化了多航天器多目标空间碎片清除问题.Shen等[123]也使用蚁群算法，同时借用摄动带来的轨道面漂移.Petropoulos等[7]使用遗传算法将蚁群算法得到的结果再次进行优化，求解了第九届国际空间轨道设计竞赛的空间碎片清除问题，取得了第一名的成绩.因此，充分利用各个算法的优势，如蚁群算法能够快速构建较优的可行解，以及遗传算法能够在已有解的基础上进一步优化，将是求解优化问题的一个重要思路.

5 结论

本文针对多目标空间探测轨迹优化问题，对转移轨迹优化和探测序列优化两个部分的智能方法进行了综述.转移轨迹优化中智能方法有着大量的应用，相比于其他优化方法(间接法等)，智能方法的优势在于其不需要梯度信息，而且全局性较好，同时应对复杂约束的能力较强.在转移轨迹快速评估方面，已有解析的方法，由于其在为了解析而做的简化过程中会丢失部分信息，导致其精度存在瓶颈，因此智能方法会是一个突破口.未来的研究可以考虑将动力学性质与智能方法相结合，比如将解析推导与训练神经网络结合，使神经网络学习到轨道转移问题中的本质规律，而不只是数据的映射关系，再将其应用如转移轨迹快速评估等航天动力学的问题中.探测序列优化中，树搜索算法的优点在于其可以构建一个庞大的搜索树，进化计算的优点在于其全局反馈机制可以减少贪婪的情况，同时其随机性使得进化计算具有更好的全局性，二者的结合将有望进一步提升全局优化算法的性能.对于实时优化问题，转移轨迹实时优化已有相关研究，但是面对复杂约束未知环境等的实时优化仍是难点，而探测序列实时优化研究较为空白，设想未来可能存在大量航天器同时进行多目标探测任务(大量航天器进行空间碎片清除或者小行星采矿)，探测序列实时优化将是一个充满挑战的研究方向.