教育人力资本与社会保障“增长陷阱”的跨越

张明 柯占莲

【摘要】在建设多层次社会保障体系过程中， 防范社会保障“增长陷阱”成为经济可持续发展不得不重视的问题， 而教育人力资本成为一国能否跨越社会保障“增长陷阱”的门槛。 基于2011 ～ 2019年29个新兴市场国家面板数据， 采用面板门槛效应方法检验社会保障对生产率的影响是否存在教育人力资本的“门槛”， 随后采用动态面板模型GMM估计方法检验“门槛效应”的具体表现。 研究发现， 社会保障对生产率的影响存在教育人力资本的“单一门槛”： 当教育人力资本水平较低时， 社会保障支出会导致经济陷入“增长陷阱”而难以持续增长; 当教育人力资本水平较高时， 社会保障支出会促进生产率提升。 采用动态面板模型GMM估计进行稳健性检验， 这一结论依然成立。

【关键词】教育人力资本;社会保障;增长陷阱;生产率;新兴市场国家

【中图分类号】D57      【文献标识码】A      【文章编号】1004-0994（2022）14-0133-7

一、引言

目前， 新兴市场国家社会保障制度逐步完善， 部分欧洲和拉美新兴市场国家已经建成规模庞大的社会保障体系[1] 。 以2019年社会保障支出占国内生产总值（GDP）比值为例： 罗马尼亚社会保障支出占比11.84%; 波兰社会保障支出占比17.39%; 巴西社会保障支出占比达18.33%。 社会保障支出逐渐发展成为新兴市场国家公共财政最大的支出项目。 一方面， 社会保障支出的增加能降低居民不确定性预期， 发挥社会稳定器的功能; 另一方面， 社会保障规模扩大导致新兴市场国家财政压力居高不下和经济增长乏力。 从世界各国社会保障制度改革发展路径来看， 拉美国家模仿发达国家社会保障制度而陷入“增长陷阱”， 与北欧福利国家依托社会保障保持国家高竞争力形成鲜明对比[2] 。 我国作为新兴市场国家中快速发展的经济体， 同样面临社会保障支出阻碍经济发展的现实困境。 因此， 在经济可持续发展过程中必须防范社会保障“增长陷阱”。

传统观点认为， 社会保障支出与教育人力资本正相关， 因为社会保障资金再次分配能够改善家庭成员教育条件， 提升家庭成员文化水平和综合素质[3] ， 同时教育人力资本通过提高劳动生产效率促进经济发展。 换言之， 教育人力资本在社会保障与生产率之间可能起中介作用。 本研究认为， 在社会保障支出影响生产率的作用中， 存在教育人力资本门槛： 一国教育人力资本水平较低时， 社会保障支出更多扮演社会稳定器的角色， 并不能明显促进生产率提高; 但当一国教育人力资本水平较高时， 社会保障支出则能发挥激励劳动者提高生产效率的作用。

本研究将基于2011 ～ 2019年29个新兴市场国家面板数据， 采用面板門槛效应和动态面板模型GMM估计方法检验教育人力资本的“门槛效应”是否存在及其具体表现。

二、文献综述

对于社会保障与经济增长的关系， 早期研究主要围绕社会保障对储蓄与投资的影响层面展开分析。 Barro[4] 从父母利他主义代际转移机制角度出发， 提出社会保障不会扭转家庭经济预算结构， 从而在家庭储蓄中发挥边际储蓄效应。 Feldstein[5] 提出社会保障通过正向“挤入储蓄”效应和反向“挤出储蓄”效应调节居民生命周期储蓄。 一方面， 社会保障资金筹集采用现收现付制模式为劳动者提供稳定的退休待遇， 可能激励居民提前退休。 劳动者提前退休将使工作期缩短， 退休期拉长， 这反过来激励其在劳动期追求高储蓄率。 另一方面， 社会保障制度为劳动者提供稳定的退休待遇， 可能会因此降低劳动者工作期财富积累， 减少个人储蓄。 社会保障制度实施过程中， 反向“挤出储蓄”效应大于正向“挤入储蓄”效应， 说明社会保障不利于居民储蓄。 沿袭这一思路， 国内不少学者也展开了相关研究。 孙祁祥和肖志光[6] 认为社会保障与投资储蓄率之间不能有效协调， 可能导致国家面临“储蓄不足型”失衡问题。 郭凯明和龚六堂[7] 认为社会保障对家庭供养具有明显的替代作用， 即社会保障通过向居民提供养老保险替代家庭养老， 由此降低家庭资金支出压力， 促进家庭经济投资。 此外， 黄少安等[8] 利用跨国数据研究发现， 社会保障支出与经济增长之间呈现负向或倒U型关系， 较强的社会保障支出刚性挤占了国家用于生产投资的储备资本， 削减国家经济继续向前发展的物质基础。

近年来， 随着内生性增长理论研究大量涌现， 社会保障与经济增长关系的研究视角发生转变， 社会保障对人力资本的影响越发引人关注。 不少学者认为社会保障会通过提高人力资本积累来提升劳动生产效率， 为经济可持续发展提供动力[9，10] 。 Kemnitz等[11] 引入代际转移理论， 认为社会保障筹资模式使父母养老保险由当期正在工作的下一代人缴费支付。 年轻父母为弥补子女未来因缴纳社会保障税费而造成的福利损失， 会进一步加大对子女的教育投资， 提高子女受教育程度[12] 。 牟娟[13] 认为当政府的社会公共支出规模不断扩大、投资公共教育的资金比例提升， 人力资本积累的程度随之加深， 进而带动社会整体生产效率提升。 部分学者则认为完善的社会保障制度严重阻碍了教育投资， 抑制了经济发展潜力。 社会保障制度已构建完善的养老“安全网”， 解决了父母养老后顾之忧， 促使父母脱离对子女赡养的依赖， 此时父母基于利己动机可能会降低对子女教育的投资[14] 。 Ehrlich等[15] 采用跨国面板数据研究发现， 社会保障制度降低了教育人力资本投资水平。 贾俊雪等[16] 认为社会保障与长期经济增长存在负向抑制效应， 这主要是由于社会保障对长期人力资本积累具有负向影响。 Caliendo等[17] 则指出健全的社会保障体系可以通过降低子女教育生命周期经济回报对父母的吸引力， 使得教育人力资本积累缩减。 而且， 随着社会保障缴费率提升， 教育投资率反向增加速度上升。

本文认为在社会保障支出与生产率及经济增长的关系中， 教育人力资本不仅起到中介作用， 还存在门槛效应。 一国教育人力资本水平较低时， 社会保障支出起社会稳定器作用， 并不能推动生产率提升; 但当一国教育人力资本水平较高时， 社会保障支出则能激励劳动者提高生产效率。 本研究将基于2011 ～ 2019年29个新兴市场国家面板数据， 采用面板门槛效应和GMM估计方法检验教育人力资本的“门槛效应”是否存在及具体表现。

三、变量说明

（一）生产率： 经济可持续性的衡量

对于生产率的测度已经由单要素转向全要素， 全要素生产率的增长是影响经济可持续发展的决定性因素。 以往学者普遍使用索洛剩余法衡量全要素生产率， 然而， 剩余法无法满足提前假设函数形式及其分布等数学条件。 因此， 在现实应用中， 学术界更加倾向于基于非参数DEA方法的Malmquist非参数方法指数法。

本文在界定全要素生产率时， 参考非参数DEA的方法以产出指标为Malmquist生产率指数。 假定存在N个决策单元， 各决策单元i在每时期（t=1，…，T）有k种要素投入， M种产出， 生产技术集St将要素投入xt∈      转化为产出yt∈      ， 用集合可表示为：

St={（xt，yt）： xt 可以生产 yt}  （1）

式（1）中， St也可称为生产可能性集合， 每当给定输入的最大输出子集， 亦称为生产技术前沿。 定义t时期的输出距离函数为：

（xt，yt）=inf{θ：（xt，yt/θ）∈St}=（sup{θ：（xt，θyt）∈St}）-1     （2）

一般来说，    （xt，yt）≤1。 当    （xt，yt）=1时， 显示此时的决策单元i处在技术前沿面上， 其全要素生产效率为1， 说明已经达到了输入的最优输出值。 接下来， 为显示生产效率时间波动， 列出不同时刻下的距离函数：

M0（xt+1，yt+1，xt，yt）=[                           ]     （3）

式（3）是t时期和t+1时期的两个不同时间节点上， 以生产技术为参照的Malmquist指数。 为了防止抉择生产技术参照系的任意性， 继续利用这两个不同时刻的距离函数求其平均数， 作为最终的Malmquist生产率指数， 即：

M0（xt+1，yt+1，xt，yt）=                      ×

（4）

采用線性规划的方法求解各个距离函数， 再利用式（4）即可得到各决策单元的Malmquist生产率指数。

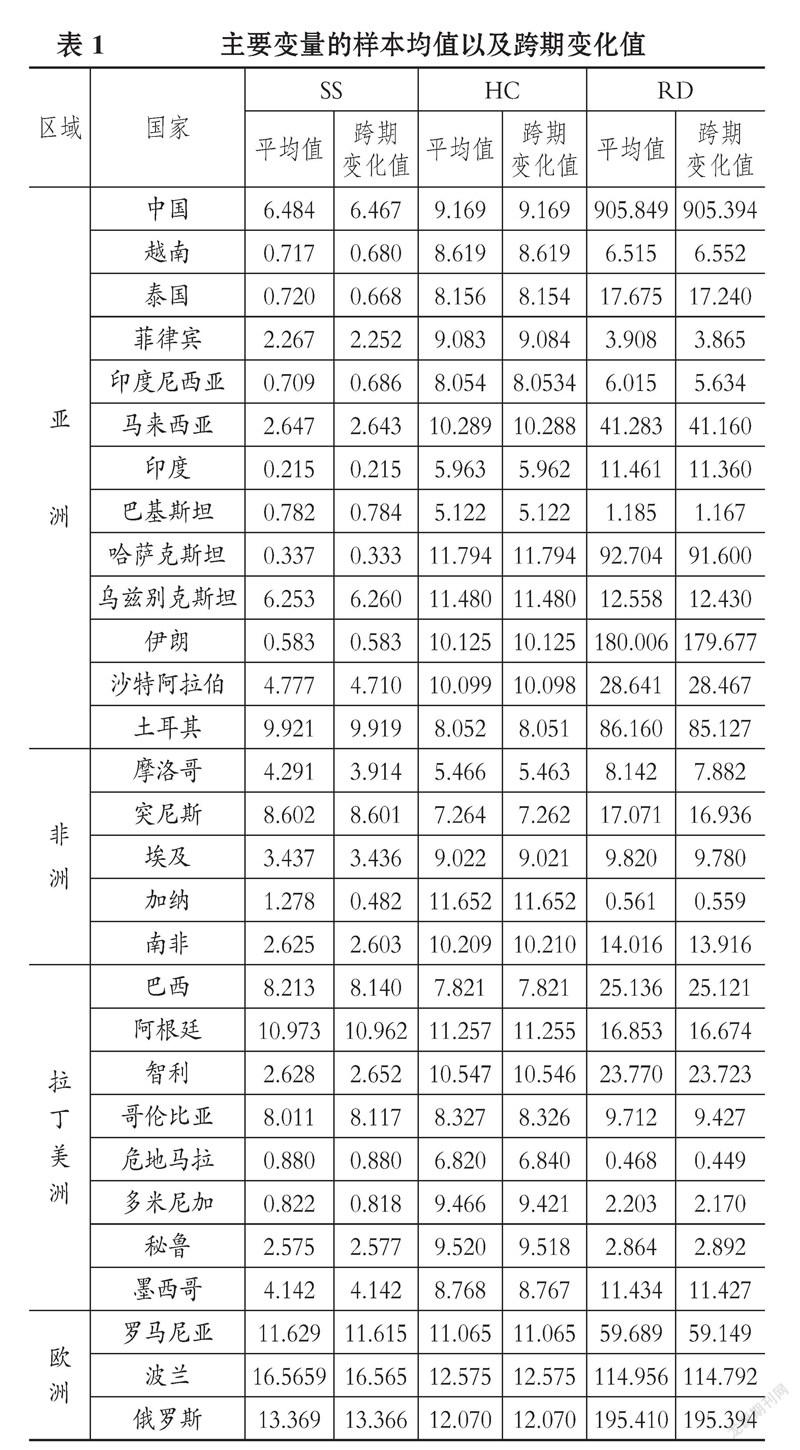
采用世界银行数据库分组中关于新兴市场国家的标准， 结合数据的可得性， 本研究选择29个新兴国家作为研究样本， 囊括亚洲、非洲、拉丁美洲以及欧洲等不同区域。 其中： 亚洲区域国家包括中国、越南、泰国、菲律宾、印度尼西亚、马来西亚、印度、巴基斯坦、哈萨克斯坦、乌兹别克斯坦、伊朗、沙特阿拉伯、土耳其等; 非洲区域国家包括摩洛哥、突尼斯、埃及、加纳、南非等; 拉丁美洲区域国家包括巴西、阿根廷、智利、哥伦比亚、危地马拉、多米尼加共和国、秘鲁、墨西哥等; 欧洲区域国家包括罗马尼亚、波兰、俄罗斯等。

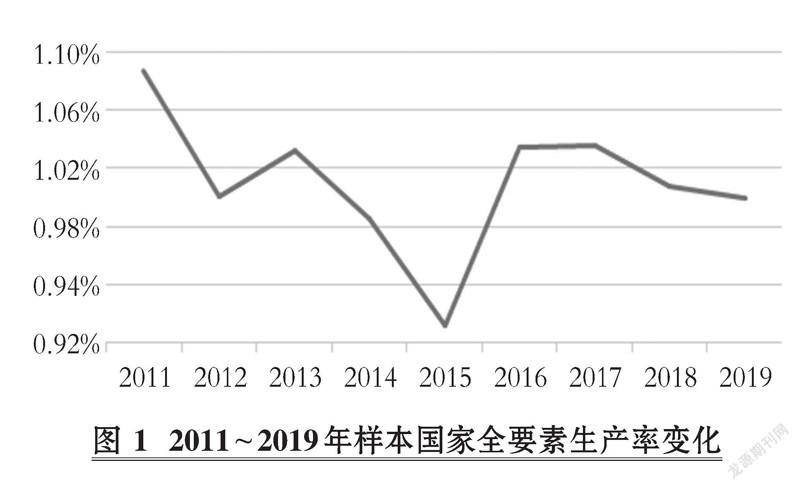
以这29个新兴市场国家作为决策单元， 时刻t=2011，…，2019， 以资本投入量和劳动力作为生产输入要素集合x， 将各个国家国民生产总值（GDP）作为输出要素y①。 选择DEA非参数Malmquist指数方法， 利用Stata 16程序计算获得29个新兴市场国家2011 ～ 2019年全要素生产率变化指数（TFPCH）。 图1显示， 9年来新兴市场国家生产率整体呈缓慢上升态势， 环比增长率均为正值， 年均上升1.01%。 这与张宗新和李东宪[20] 的测算结果相似。

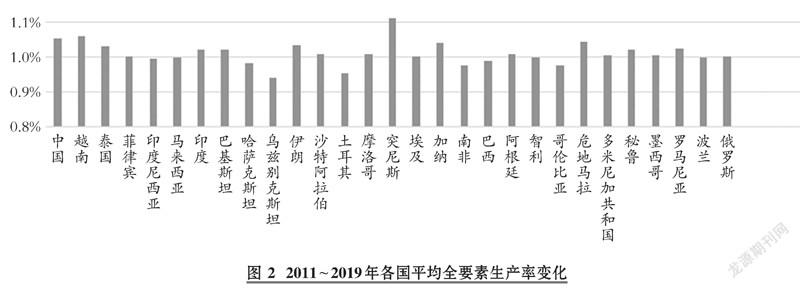
为进一步观察新兴市场国家生产率变化特征， 本研究考察了各样本国家的全要素生产率变化。 图2显示， 样本跨期内， 新兴市场国家的生产率都出现了增长趋势。 其中中国、突尼斯、越南、加纳、危地马拉以及罗马尼亚等国家生产率增长明显， 这与其国家经济发展投资战略相关。 自2008年金融危机以来， 这些国家积极调整经济政策， 以应对危机带来的负面经济影响， 不仅将财政收入投向基础设施建设以及民生社会保障， 而且注重人力资本等软实力的不断提升， 从而实现了生产率的快速增长。

（二）社会保障与教育人力资本等变量

1. 社会保障（SS）。 学者普遍采用社会保障支出占国民生产总值（GDP）的比重来衡量社会保障， 本文也使用这一统计口径。 数据来自于国际货币基金组织（IMF）。

2. 教育人力资本（HC）。 Lucas[21] 构建的专业化人力资本积累经济增长模型， 引起学界对人力资本与经济增长之间关系的广泛研究。 根据前文预设， 社会保障影响经济增长存在教育人力资本门槛效应。 教育人力资本变量主要采用国民平均受教育年限来测度。 各国平均受教育年限数据来源于联合国教科文组织（UNESCO）②。 本文还控制了其他影响生产率的因素， 例如研发（RD）。 根据Romer[22] 的内生增长理论， 研发投入越高的国家， 其生产率增长越快， 从而能够实现持续的经济增长。 用各国每一百万人中三项专利授权数作为研发变量指标， 数据来源于世界银行（World Bank）。

表1报告了社会保障（SS）、教育人力资本（HC）以及研发（RD）三个解释变量在2011 ～ 2019年间的平均值以及跨期变化值。 表1显示， 欧洲、拉丁美洲国家的社会保障支出和教育人力资本水平明显高于亚洲和非洲各国， 这与这些国家一直以来努力打造福利国家有关。 就教育人力资本变量和研发变量而言， 在欧洲和亚洲各个国家这两个指标明显高于非洲和拉丁美洲， 这同样与欧洲和亚洲国家对于教育和研发的重视密切相关。

四、门槛效应检验

本文认为社会保障对生产率的影响存在教育人力资本的门槛效应， 因此， 依据面板数据门槛回归模型， 探究教育人力资本的门槛效应是否存在。 门槛模型是根据单个变量（门槛变量）的特定指数（门槛值）对样本进行划分， 随后以严格的统计推断方法对门槛值进行参数估计和显著性统计检验， 以此描述门槛模型参数的非线性转换， 继而协助检验社会保障影响生产率的非线性特点。 确定门槛值的传统做法是由研究者主观随意确定一个值， 然后据此门槛值将样本一分为二， 或者分为更多子样本进行测算。 显然， 这样获得的结果并不具科学性。 因此， 为规避人为划分门槛值可能造成测算结果失真的问题， 本文采用Hansen[23] 的面板门槛模型， 并根据29个国家数据自身的特点来内生测算门槛值与其转换区间， 研究社会保障影响生产率的非线性结构。 以单一门槛模型为例， 基准模型如下：

TFPCHit=αi+β1SSit×I（HCit≤γ）+β2SSit×

I（HCit>γ）+ϕ×Xit+εit  （5）

式（5）中， 下标i表示省份、t表示年份。 TFPCH、SS分别为被解释变量全要素生产率和解释变量社会保障。 HC是门槛变量即教育人力资本。 X包括全要素生产率一阶滞后项（TFPCH-1）、教育人力资本（HC）和研发（RD）， γ是待估门槛值。 I（∙）为示性函数， 即如果括号内的表达式为假时， I（∙）取值为0， 反之取值为1。 αi表示控制不同国家样本数据中不可观测的个体特征， ε是随机扰动项。

当式（5）单一面板门槛回归模型中β1≠β2成立， 则意味着在教育人力资本较低（HCit≤γ）的样本区间和教育人力资本较高（HCit>γ）的样本区间， 社会保障（SS）对全要素生产率（TFPCH）的影响存在非线性差异。 为测算得到式（5）的结果， 先对各核心变量数据执行组内去除均值处理， 消除公式中的个体效应αi误差。 随后对变量的样本值执行聚集， 变换后的模型使用矩阵形式表现， 记作：

SS∗=X∗（γ）×β+ε∗  （6）

式（6）中， 将确定的门槛值γ代入其中进行最小二乘法（OLS）估计， 求取参数β的待估参数值：

（γ）=[X∗（γ）'X∗（γ）]-1X∗（γ）SS∗ （7）

以求得的参数β继续测算相对应的残差平方和， 用S1（γ）表示， 则：

S1（γ）=[e*]（γ）'[e*]（γ） （8）

公式（8）中， [e*] （γ）=SS∗-X∗（γ）  （γ）， 为残差向量。 而S1（γ）也是门槛值γ的阶梯函数， 且γ的取值不会对子样本的划分产生影响， 由此可以搜索获得S1（γ）最小时所对应的γ值， 即：

S1（γ）  （9）

进而可以得到              ， 残差               ， 残差平方和                。

得到参数估计值后， 需要执行门槛效应是否显著的检验。 针对式（5）的原假设为： H0：β1=β2， 构造的F统计量为：

[F=S0-S1  （γ）σ2 ]      （10）

式（10）中， S0是由H0获得的残差平方和。 如果原假设H0：β1=β2成立， 则无论γ取什么值， 对模型均不产生影响， 门槛值γ无法识别。 故F统计量的渐进分布是非标准的， 而依赖于样本距， 无法识别其临界值列表。 据此， Hansen[23] 提出采用“自助法”（Bootstrap）获得其渐进分布和相应的P值。

式（5） ～ （10）只分析讨论存在单一门槛值的情况。 当模型中存在两个及两个以上特定门槛值， 可以将以上推断过程继续拓宽处置。 以面板门槛回归模型中存在两个门槛值γ1、γ2为例， 首先测算第一个门槛估计值    ， 并假设该值既定， 再同样执行式（5） ～ （10）搜索第二个门槛值γ2。 待門槛值γ1、γ2的估计值确定后， 将其代入式（5）中， 面板门槛模型具体表现形式随即呈现。 此时可以进一步估计模型参数以及进行门槛参数统计推断和假设验证。

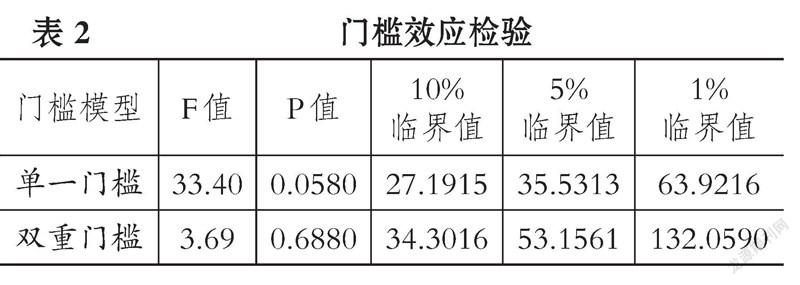
基于Hansen[23] 的方法， 本文设定没有门槛值、一个门槛值、两个门槛值以及三个门槛值， 执行模型假设检验， 搜寻模型具体的门槛数目， 并将不同门槛个数和不同形式回归模型所对应的F统计量记录在表2中， 概率P值和不同临界值通过“自助法”（Bootstrap）重复抽样1000次获得。 表2显示单一门槛效应显著， 相应的概率P值为0.058， 而双重门槛效应不显著， 概率P值为0.688。 因此， 模型设定为单一门槛回归模型， 门槛估计值为7.0029， 95%置信区间为6.8286 ～ 7.2768， 具体列于表3。 综上所述， 社会保障对生产率的影响的确存在教育人力资本 “单一门槛”效应。

五、门槛效应的具体影响表现

（一）计量模型设定

为了减小解释变量的内生性以及遗漏变量带来的估计偏误的影响， 本文并没有直接根据Hansen[23] 得到的门槛效应模型计算社会保障对生产率影响的估计系数， 而是设计动态面板模型， 并通过交叉项的设置来判断门槛效应的具体表现。 本文同样控制了全要素生产率的一阶滞后项， 并在模型中引入社会保障与教育人力资本交叉项。 具体表现形式如下：

TFPCHit=β0+ρTFPCHit-1+β1SSit+β2RDit+

φSSit×HCit+θYEAR+β4ASIAN+β4EUR+εit （11）

上式中， SS×HC表示社会保障与教育人力资本交叉项， 若SS×HC的估计系数φ显著且为正时， 代表社会保障对生产率的影响可能存在假设中提到的教育人力资本的门槛。 YEAR代表时间虚拟变量， 以此来控制截面数据相依性。 另外， 本文所列区域的新兴市场国家综合国力大有不同， 各国之间经济发展水平同样存在明显差异， 所以在模型中设置亚洲虚拟变量（ASIAN）和欧洲虚拟变量（EUR）以控制欧洲、亚洲和其他区域之间的显著异质性。

式（11）将采取动态面板模型GMM估计方法进行测算。 动态面板模型GMM估计方法包括一步（One-Step）和两步（Two-Step）GMM估计。 但数据推理结果表明， 两步GMM估计的权重矩阵依赖估计参数且标准差存在向下偏倚， 所以两步GMM估计量也不可靠。 一步估计量尽管效率有所下降但它是一致的， 所以在经验应用中通常使用一步GMM估计量。 本文使用的动态面板模型最终为一步差分GMM和一步系统GMM估计。

（二）估计结果与分析

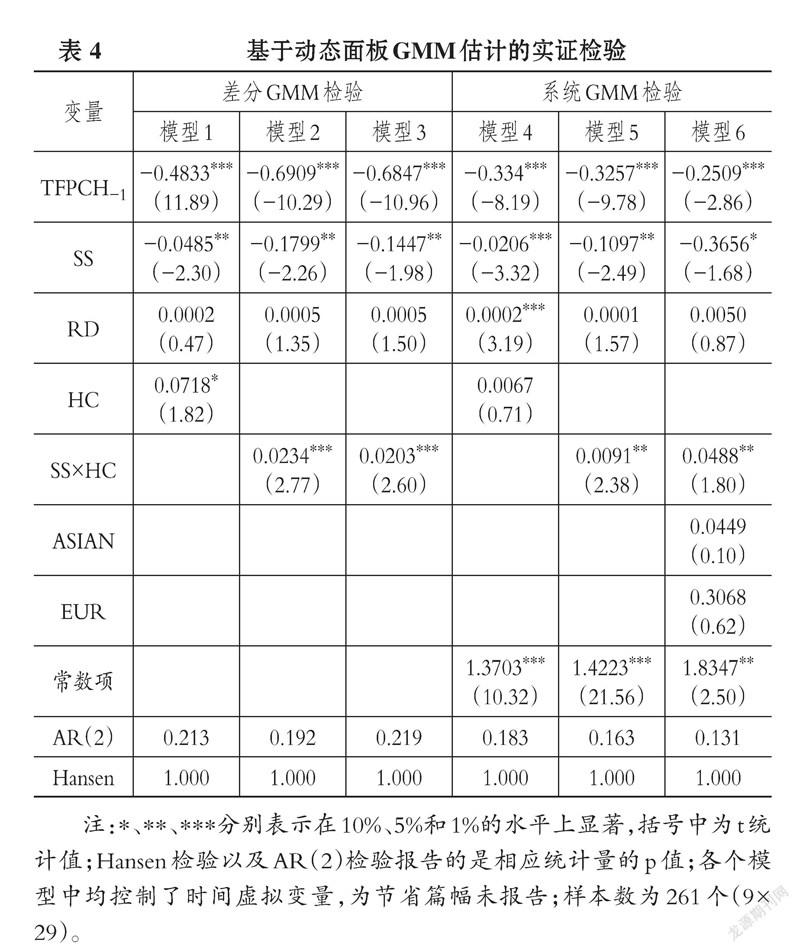
在采用动态面板GMM模型进行估计前， 首先对各变量进行单位根检验。 本文同时采用同质的LLC检验与异质的IPS检验对主要变量进行单位根检验。 单位根检验结果表明， 文章采用的变量都是平稳的（限于篇幅， 正文没有报告）。 接下来同时运用一步差分GMM和一步系统GMM方法对模型（11）进行估计， 结果见表4。 表4中模型1、模型2和模型3是一步差分GMM的估计结果， 其中， 在模型1中引入了全要素生产率一阶滞后项（TFPCH-1）、社会保障（SS）、研发（RD）和教育人力资本（HC）等变量， 在模型2中引入了全要素生产率一阶滞后项（TFPCH-1）、社会保障（SS）、研发（RD）以及社会保障与教育人力资本的交叉项（SS×HC）， 模型3在模型2的基础上进一步控制了时间与区域变量。 模型4、模型5和模型6是对应的一步系统GMM的估计结果。 在表4中， 社会保障（SS）的估计系数都为负且显著， 但社会保障与教育人力资本的交叉项（SS×HC）估计系数显著为正， 这说明社会保障对生产率增长的影响存在教育人力资本的门槛： 当教育人力资本水平较低时， 社会保障会使经济陷入“增长陷阱”而难以持续增长; 但随着教育人力资本水平提升， 社会保障支出进一步激发劳动者生产效率从而提升生产率。 动态面板模型GMM估计验证了本文的预期假设。

六、结论与政策建议

近十几年来， 新兴市场国家的社会保障覆盖面不断扩大， 社会保障支出逐渐成为各国公共财政最大的支出项目。 同时， 社会保障支出持续扩大可能会导致政府债务的无限制增长， 削弱经济发展效率。 而教育人力资本作为社会经济发展的核心资源， 通过“效率提升”促进经济增长[24] ， 对提高生产率产生积极的推动作用。 本研究基于2011 ～ 2019年新兴市场国家面板数据， 发现社会保障对生产率的影响存在教育人力资本的“单一门槛”。 本文进一步采用动态面板模型GMM估计方法检验， 发现这种门槛效应真实存在， 即当教育人力资本水平较低时， 社会保障会使经济陷入“增长陷阱”而难以持续增长; 但随着教育人力资本水平提升， 社会保障支出激发劳动者生产效率从而提升生产率的作用得以显现。

本文实证研究的政策含义是明显的。 一方面， 本文发现当教育人力资本处于低水平时， 社会保障支出可能促使经济体迈入“增长陷阱”， 部分新兴市场国家目前很可能还处于这一陷阱之中。 因此， 各国必须加快对教育人力资本的积累来走出这一陷阱。 这就要求新兴市场国家要把财政资金投向国民教育等有助于人力资本增长的领域， 这是跨越经济增长陷阱的重要途径。 特别是结合目前新兴市场国家依然存在教育人力资本水平区域不均衡、差异大等现实问题， 进一步要求新兴市场国家将财政支出向教育落后的地区倾斜， 促进国民人力资本积累。 另一方面， 必须注意社会保障支出与教育人力资本之间的协同。 适度的社会保障水平有利于经济可持续增长， 但过度的社会保障反而不利于生产率的提升。 近些年部分新兴市场国家经济增长乏力可能与社会保障的过度支出有关。 因此， 新兴市场国家在健全社会保障制度时要注意维持社会保障支出的适度规模， 协调好社会保障支出規模与教育人力资本积累之间的关系， 促进二者良性循环。

【 注 释 】

① 国民生产总值、劳动力（从业人数）数据来自历年的世界银行（World Bank），各国国民生产总值均转换为以2009年为基期的不变价格数据。本文中计算全要素生产率增长率所使用的变量为：产出（Y），采用国民生产总值（GDP）衡量;资本投入量（K）采用年度固定资本形成总额，并使用永续盘存法进行核算，其公式为Kt+1=Kt（1-δt+1）+It+1。其中δt+1是t+1期折旧率，参照Hall和Jones[18] 研究跨国资本存量时所采取的通用折旧率6%，It+1则为t+1期固定资本形成总额。Kt是根据Angel和Doménech[19] 的测算方法测算的基期资本存量，即：Kt=It+1（1+gk）/（gk+δ）。gk是资本存量的增长速度，用投资增长速度gi进行估计，即gk=gi，是以2009年为基期的不变价格数据。

② 中国平均受教育年限测算原始数据来自历年的《中国人口年鉴》和《中国人口和就业统计年鉴》。计算时，小学毕业计6年，初中毕业计9年，高中毕业计12年，大专及以上学历计16年，文盲记为0。

【 主 要 参 考 文 献 】

[1] 林卡.收入差距和社会公正：拉美国家社会保障体系的发展及其经验[ J].社会科学，2011（10）：62 ～ 68.

[2] 周弘，彭姝祎.国际金融危机后世界社会保障发展趋势[ J].中国人民大学学报，2015（3）：26 ～ 34.

[3] Pietro G. D.. Equality of Opportunity in Italian University Education： Is There Any Role for Social Welfare Spending[ J].International Journal of Educational Development，2003（1）：5 ～ 15.

[4] Barro R. J.. Government Spending in A Simple Model of Endogenous Growth[ J].Journal of Political Economy，1990（5）：103 ～ 126.

[5] Feldstein M.. Social Security， Induced Retirement， and Aggregate Capital Accumulation[ J].Journal of Political Economy，1974（5）：905 ～ 926.

[6] 孙祁祥，肖志光.社会保障制度改革与中国经济内外再平衡[ J].金融研究，2013（6）：74 ～ 88.

[7] 郭凯明，龚六堂.社会保障、家庭养老与经济增长[ J].金融研究，2012（1）：78 ～ 90.

[8] 黄少安，陈言，李睿.福利刚性、公共支出结构与福利陷阱[ J].中国社会科学，2018（1）：90 ～ 113.

[9] Sala-I-Martin X.. A Positive Theory of Social Security[ J]. Scandinavian Journal of Economics，1996（2）：277 ～ 304.

[10] 范静泊，杨天宇.社会福利支出、人力资本与中国经济增长——基于省际面板数据的研究[ J].当代经济管理，2012（7）：13 ～ 18.

[11] Kemnitz A.， B. U. Wigger. Growth and Social Security： The Role of Human Capital[ J].European Journal of Political Economy，2000（4）：673 ～ 683.

[12] Mimoun M. B.， A. Raies. Education and Economic Growth： The Role of Public Expenditures Allocation[ J].Economics Bulletin，2009（3）：2404 ～ 2416.

[13] 牟娟.社会保障、人力资本支出对经济增长的统计检验[ J].统计与决策，2020（13）：116 ～ 120.

[14] Ehrlich Isaac， Zhong Jian-Guo. Social Security and the Real Economy： An Inquiry into Some Neglected Issues[ J].American Economic Review，1998（2）：151 ～ 157.

[15] Ehrlich I.， J. Kim. Social Security， Demographic Trends， and Economic Growth： Theory and Evidence from the International Experience[ J].Review of Economic Dynamics，2007（1）：55 ～ 77.

[16] 贾俊雪，郭庆旺，宁静.传统文化信念、社会保障与经济增长[ J].世界经济，2011（8）：3 ～ 18.

[17] F. Caliendo， Findley T. S.. Myopia，Education，and Optimal Social Security[Z]. SSRN Working Paper，2018.

[18] Robert E. Hall， Charles I. Jones. Why Do Some Countries Produce So Much More Output Per Worker Than Others？[ J].The Quarterly Journal of Economics，1999（1）：83 ～ 116.

[19] Angel Fuente， Rafael Doménech. Human Capital in Growth Regressions： How Much Difference Does Data Quality Make？[ J].Journal of the European Economic Association，2006（1）：1 ～ 36.

[20] 張宗新，李东宪.融资结构、经济效率与金融稳定性——基于新兴市场国家面板数据的实证检验[ J].上海金融，2019（12）：19 ～ 30.

[21] Lucas R. E.. On the Mechanics of Economic Development[ J].Journal of Monetary Economics，1988（1）：3 ～ 42.

[22] Romer M. P.. Endogenous Technological Change[ J].The Journal of Political Economy，1990（1）：71 ～ 102.

[23] Hansen B. E.. Threshold Effects in Non-Dynamic Panels： Estimation， Testing， and Inference[ J].Journal of Econometrics，1999（2）：345 ～ 368.

[24] 杜育红，赵冉.教育在经济增长中的作用：要素积累、效率提升抑或资本互补？[ J].教育研究，2018（5）：27 ～ 35.

【基金项目】国家社会科学基金项目（项目编号：20FGLB006）

【作者单位】西南大学国家治理学院， 重庆 400715