黄水沟汛期逐月流量过程的聚类分型与定性预报

苏 仁，旦木仁加甫

(1.新疆巴音郭楞水文勘测局，新疆 库尔勒 841000；2.新疆水文局，新疆 乌鲁木齐 830000)

每年年初，政府水行政主管部门要求提供河流汛期(4—9月)来水定性预报成果，由于新疆河流汛期来水集中度高(如黄水沟汛期来水占年水量的77%)、变幅大、随机性强，加之水文站网密度又稀少，导致预报精度不高。本文采用K-均值聚类分析和逐步回归周期分析技术，用黄水沟水文站历年汛期逐月流量建立预报模型，对建模期外的次年汛期逐月流量进行定性预报，确保有效提高预报精度。

1 技术思路

1.1 聚类分型

K-均值聚类分析技术常用于样本数据的聚类分型，该技术主要特点是对大样本资料指定聚类数并实现快速聚类，可由SPSS统计软件实现聚类分型：按指定的聚类数和距离最近原则对样本数据进行初始聚类分型，再进行迭代计算，直到达到聚类终止条件时的分型即为最终聚类成果。把各样本数据聚类分型值按时间顺序排列，即为用于定性预报的类型值序列。

1.2 定性预报模型

用逐步回归周期分析技术进行定性预报：对统计年限为n的类型值序列Y(t)(t为时间)，取m为n/2的整数，k=2、3、…、m+1，采用周期均值叠加法得到m个周期(长度为不同k)，把每个周期的振幅值排列为m个长度为n的序列；然后用逐步回归法对Y(t)与m个周期序列进行回归分析，通过最终引进和剔除双重检验的各周期序列就是Y(t)不同长度k的周期。预报模型为：

Y(t)=A+∑Ai×Xi(t)+ξ(t)

(1)

式中，i—周期总数；A、Ai—常数项和回归系数；Xi(t)—Y(t)通过统计检验的不同长度k的周期；ξ(t)—噪声项。

将通过统计检验的各周期振幅外延值代入(1)式，便计得相应的类隶属定性预报值。

2 分型、建模与预报

2.1 汛期逐月流量过程的分型

对黄水沟水文站1955—2019年汛期逐月流量过程进行K-均值聚类分析：根据表1所建的SPSS数据文件，依次单击菜单“分析→分类→K-均值聚类分析”，在弹出的K-均值聚类分析对话框中把逐月流量和相应年份分别选入变量和个案标记依据列表框，选择“迭代与分类”方法，设置“聚类数”为2；在迭代对话框中，设置迭代聚类上限为20，迭代聚类终止条件(即收敛标准)为0.01；在保存、统计量对话框中分别选用“聚类成员”、“每个个案的聚类信息”，其余均选用默认选项。最后通过4次迭代达到了聚类终止条件。

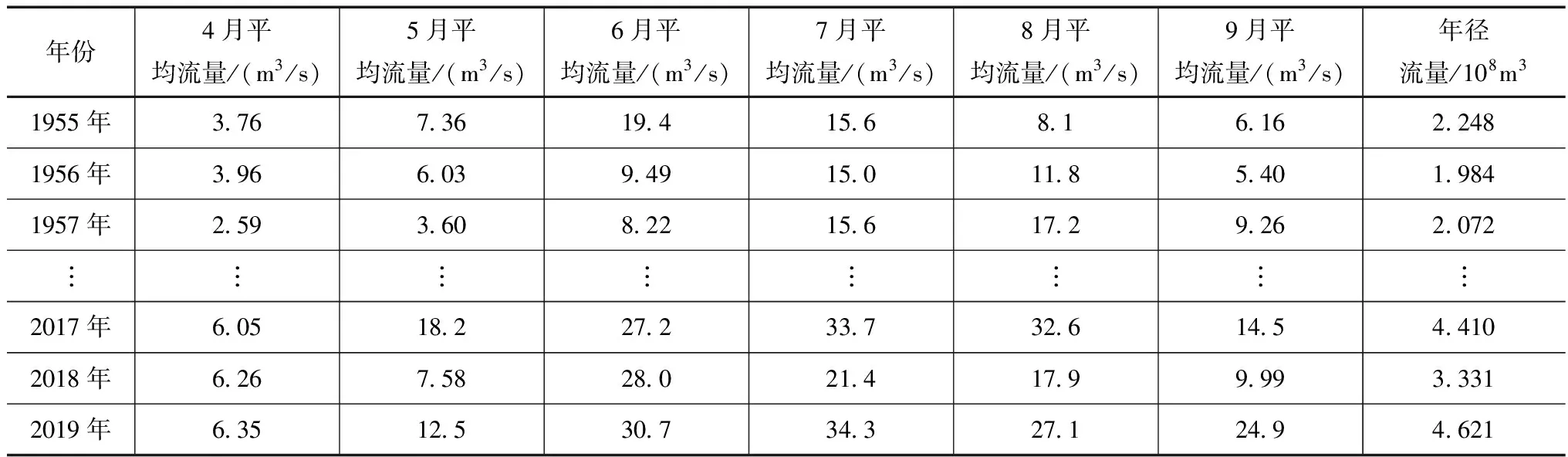
表1 黄水沟水文站汛期(4—9月)逐月流量过程

SPSS输出的统计分析结果如下。

(1)初始聚类中心

SPSS系统自动指定的2个初始类中心点见表2，其代表性不是最好，需要通过迭代过程寻找更好的类中心点来代替初始类中心点。

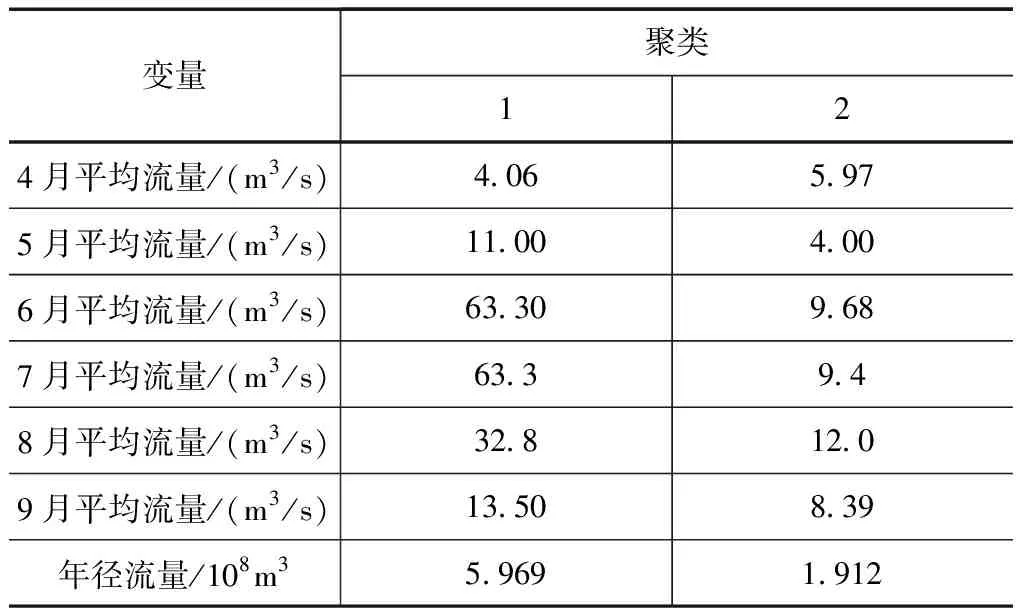
表2 初始聚类中心

(2)迭代历史记录

2个类中心每次迭代时的变化记录见表3，第4次迭代后2个类中心点变化均接近或小于指定的收敛准则(0.01)，达到聚类结果的要求，聚类分析结束。

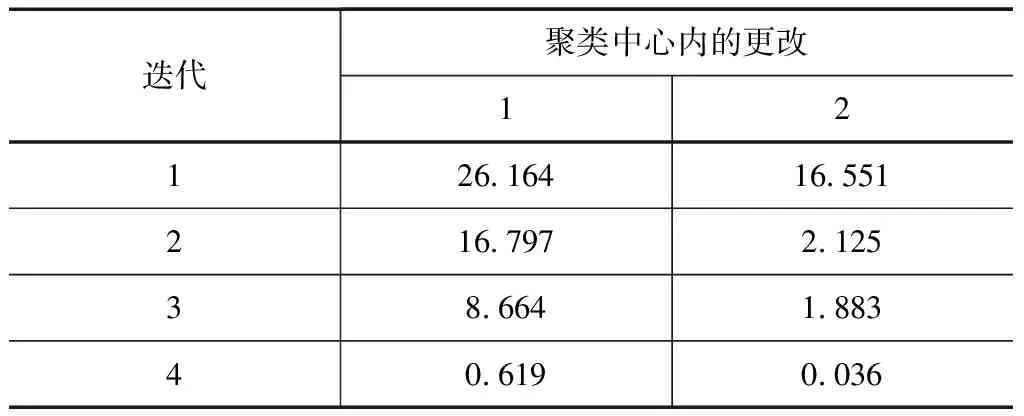
表3 迭代历史记录

(3)K-均值聚类分析的类成员

黄水沟水文站汛期(4—9月)逐月流量过程聚类成果见表4，分1、2两类，Y(t)列是类型值序列。

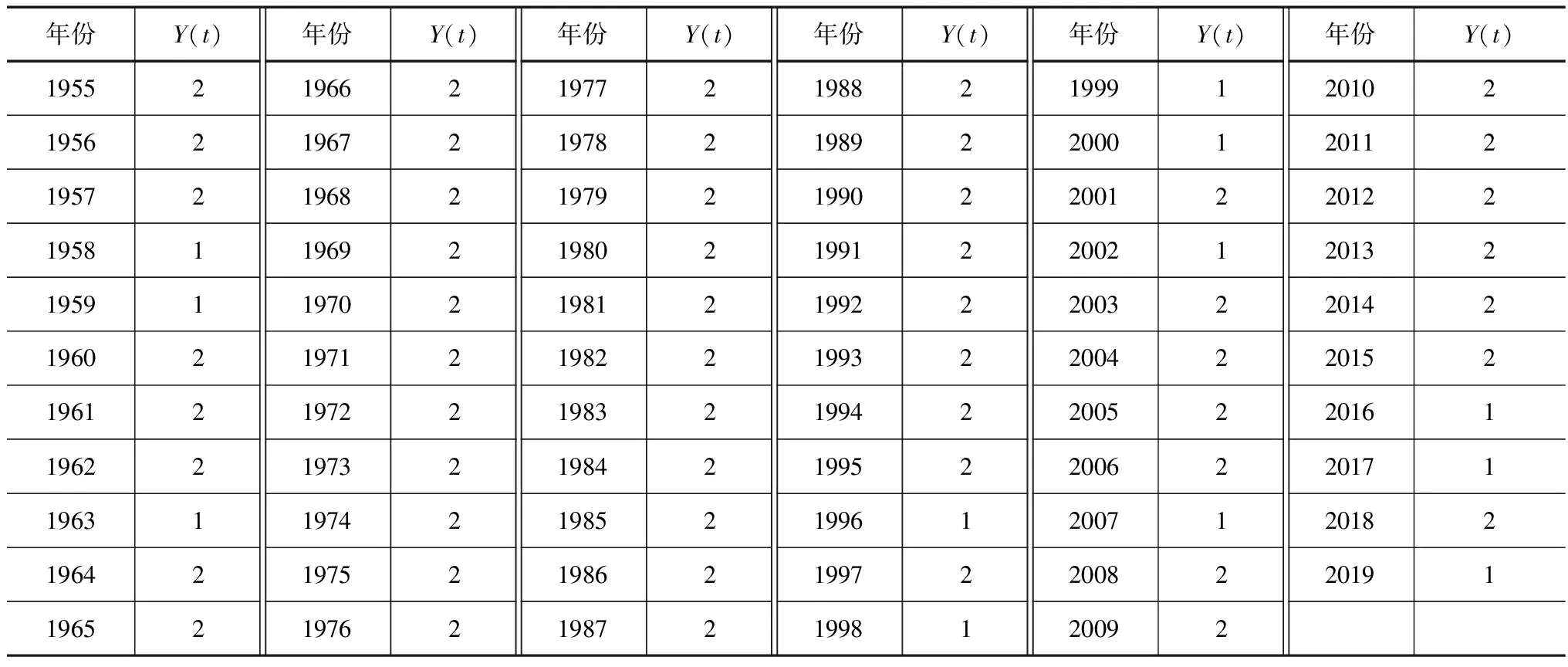
表4 黄水沟水文站汛期(4—9月)逐月流量过程聚类成果

(4)最终聚类中心

2个类的最终聚类中心见表5，可见，第1类各指标数值相对来讲较高，第2类较低。

由于黄水沟水文站汛期(4—9月)水量占年水量比例高达77%，集中度高，所以汛期水量与年水量的丰枯性是相对一致或同步的，由表5可见，类1、2多年平均年径流量分别是4.718×108m3和2.603×108m3，与黄水沟水文站多年平均年径流量2.993×108m3相比，类1年径流量显著偏丰，类2则显著偏枯，所以可以明确：类1汛期(4—9月)逐月流量过程呈现正常偏丰的特点，类2则呈现正常偏枯的特点。

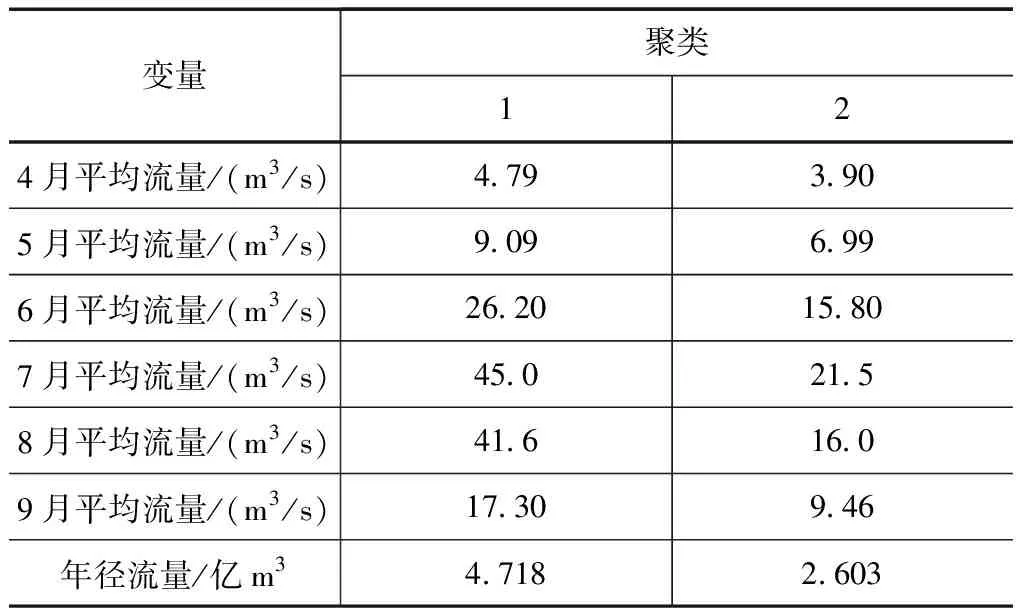
表5 最终聚类中心

(5)类成员样本数

表6显示2个类的类成员样本数情况，其中，第1类有12个汛期(4—9月)流量过程样本，第2类有53个。

表6 每个聚类中的样本数

2.2 建立定性预报模型

用逐步回归周期分析技术从表4类型值序列Y(t)中计得6个周期，见表7，其中X1(t)、X2(t)、X3(t)、X4(t)、X5(t)、X6(t)分别是长度为29、21、17、13、30、18年的第一、二、三、四、五、六周期序列(样本容量n均为65)，表内数值即为相应振幅。Y(t)具体预报模型为：

表7 逐步回归周期分析及拟合计算成果表

Y′(t)=A+∑Ai×Xi(t)

(2)

式中，Y′(t)是Y(t)的拟合值，i=1、2、…、6时，模型常数项和回归系数依序为：A=-3.2232，A1=0.5720，A2=0.5392，A3=0.4310，A4=0.5908，A5=0.3243，A6=0.3181。

F检验：n=65、信度α=0.001时，F=43.06>F(0.001)=4.40，通过相应信度的F检验，说明模型回归系数Ai为0的假设不成立，有统计学意义。

2.3 拟合检验

表7中W(t)是黄水沟水文站1955—2019年类型值序列Y(t)与相应拟合值Y′(t)之间的相对误差，其中Y′(t)由(2)式计得；若|W(t)|≤20%为合格，由表7可见，在65年拟合检验期内，仅1996、2007、2019年不合格，其它年份均合格，合格率高达95.4%，说明拟合的非常好，式(1)中ξ(t)已很平稳，计得的6个周期是有效的。

2.4 2020年汛期逐月流量过程类隶属定性预报

对Y(t)序列，取t为2020年时，对应6个周期的外延振幅依次是2、1.67、2、1.8、2和1.67，代入预报模型(2)式得Y′(2020)=1.92，与类型值1相差很大，而与类型值2十分接近，表明黄水沟水文站2020年汛期(4—9月)逐月流量过程大概率地属于类型值序列中的第2类，即呈现正常偏枯特点的可能性较大。表8是2020年汛期逐月流量实况与类隶属的判断，可见，2020年各月平均流量与类1、2流量均值相比，仅4月与类1相近，其余5个月与类2相近，表明呈现正常偏枯特点的定性预报总体正确。

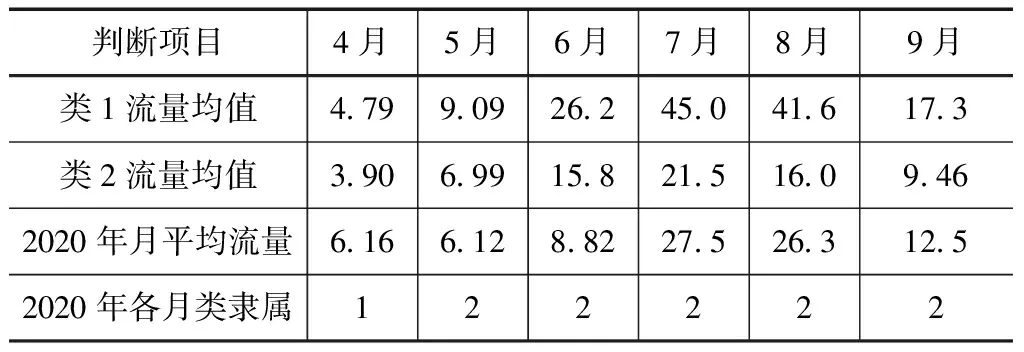
表8 2020年汛期(4—9月)逐月流量实况与类隶属的判断 单位：m3/s

3 结语

(1)仅用黄水沟水文站本站历年汛期逐月流量过程分型与建模，并对次年汛期来水类隶属进行定性预报，既不受河流汛期来水集中度高、变幅大、随机性强的影响，又规避了水文站网稀少现状的制约。

(2)类型值预报模型通过了信度为0.001的F检验，说明有统计学意义。

(3)|W(t)|≤20%为合格时，在65年拟合检验期内，合格率高达95.4%，拟合很好，表明计得的6个周期是有效的。

(4)从2020年汛期逐月流量实况与类隶属的判断来看，仅4月定性预报不合格，其余5个月均合格，表明定性预报总体正确，本文所述聚类分型与类型值预报的技术适用于长期水文定性预报。