基于融合特征选择算法的钻速预测模型研究

周长春，姜 杰，李 谦，朱海燕，李之军，鲁柳利

（1.成都理工大学环境与土木工程学院，四川 成都 610059；2.成都理工大学机电工程学院，四川 成都 610059；3.成都理工大学能源学院，四川 成都 610059；4.成都工业学院大数据与人工智能学院，四川 成都 611730）

0 引言

我国能源生产重点方向正在向超深层发展，随着钻井的深度增加，钻头进入更加复杂的地层，会使施工难度加大、钻井速度减慢、成本升高。在国内外的研究中，机械钻速一直是作为钻井作业整体水平的直观反映，准确预测机械钻速可以有效计算钻井成本和钻井时间，从而优化钻井参数、合理安排钻机工作人员，并为钻井设计人员提供依据［1］。

传统的钻速预测研究中，一些研究人员考虑岩性、竖井直径和转速等作为主要因素，通过对多元化回归的分析，获得钻速方程［2］。还有一些研究人员制作模拟和动态模型，通过试验模拟钻探时的冲击强度来调整及预测钻速［1］。随着大数据及计算机技术的发展及其被应用到油气行业，采用机器学习技术对机械钻速进行预测已成为智能钻井行业研究的有 效 方 法 和 重 要 手 段［3］。如Amer 等［4］将 钻 压、转速、排量、扭矩、泵量、泥浆密度和立管压力作为输入参数输入到基于人工神经网络的钻速预测模型。赵颖等［5］以南海YL8-3-1 井为例，使用井眼深度、钻压、大钩位置、扭矩、出入口钻井液密度和温度等基于极限学习机建立了海上钻井机械钻速预测模型。对于特征选择方法的研究方面：李莉等［6］在特征选择阶段采用核主成分分析剔除源项目中的冗余数据的方法进行建模，结果表明所选择特征会使得建模精度有一定的提高。周翔等［7］提出了大数据环境下的投票特征选择算法可以有效解决特征选择问题。康文豪等［8］提出了一种双层特征选择法进行特征选择，其结果是所选特征使得预测模型有较好的拟合效果。此外，针对机械钻速预测研究，Dupriest 等［9］强调了特征选择在建模过程中的重要性。Shi 等［10］通过对钻头钻进机制进行研究确定了包括表面测量、钻头特性、水力学变量和地层特性等10 个参数作为人工神经网络模型输入进行了研究。

综上，很多研究通过优化智能算法来提升模型精度，亦有很多研究者对大数据中特征选择方法进行了研究，然而专门针对机械钻速预测来完成特征选择部分的智能方法研究却相对较少。在进行钻速预测研究时，海量的钻井参数会耗费大量的计算资源和时间，且不易得到理想的模型精度，故亟需针对机械钻速特征选择进行专门研究。因此，本文提出一种融合特征选择法进行参数优选，再选用梯度提升树（Gradient Boosting Decision Tree，GBDT）算法进行钻速预测，并针对参数优选结果与预测精度设计对比试验进行验证。

1 基于融合特征选择钻速预测模型总体架构设计

本文先对采集到的数据进行整合预处理，然后基于设计的融合特征选择算法进行特征优选，最后针对特征优选结果建立GBDT 钻速预测模型并设计对比试验进行验证，如图1 所示。

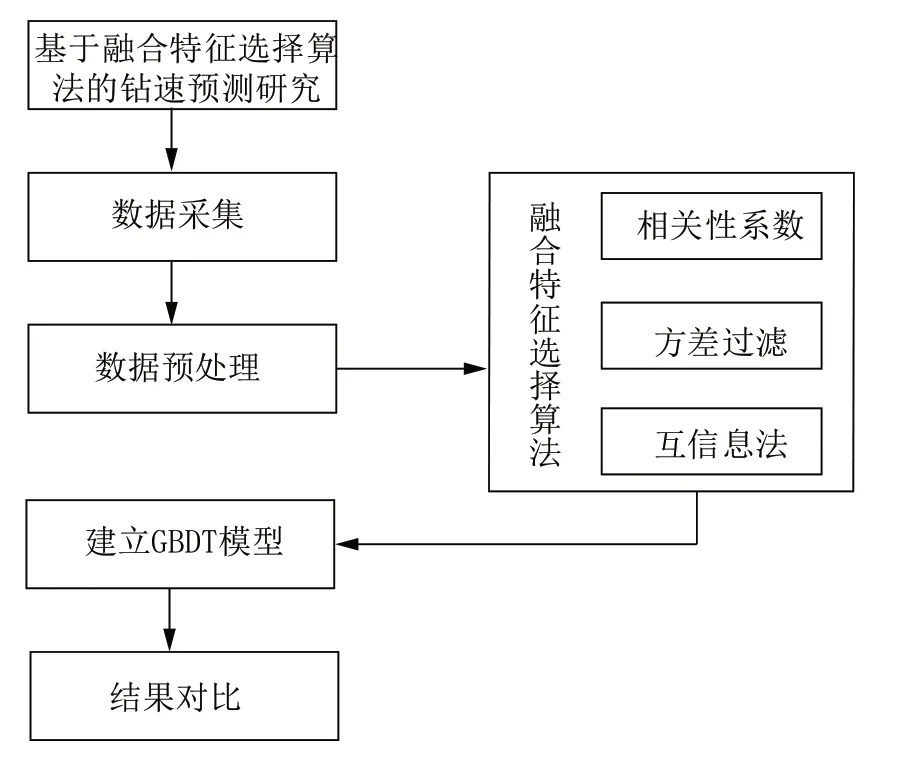
图1 融合特征选择算法钻速预测模型研究Fig.1 Research on ROP prediction model with fusion feature selection algorithm

2 数据预处理

2.1 数据采集

令钻井参数数量为n，井深为D，不同的钻井参数采集时最大密度为d，则整合后的数据矩阵为一个D/d行×n列矩阵［11］。在本文所使用的南海某井眼钻井数据共5 大类43 种不同的参数共3967 条，表1 所示为参数缩写信息和参数分类信息。

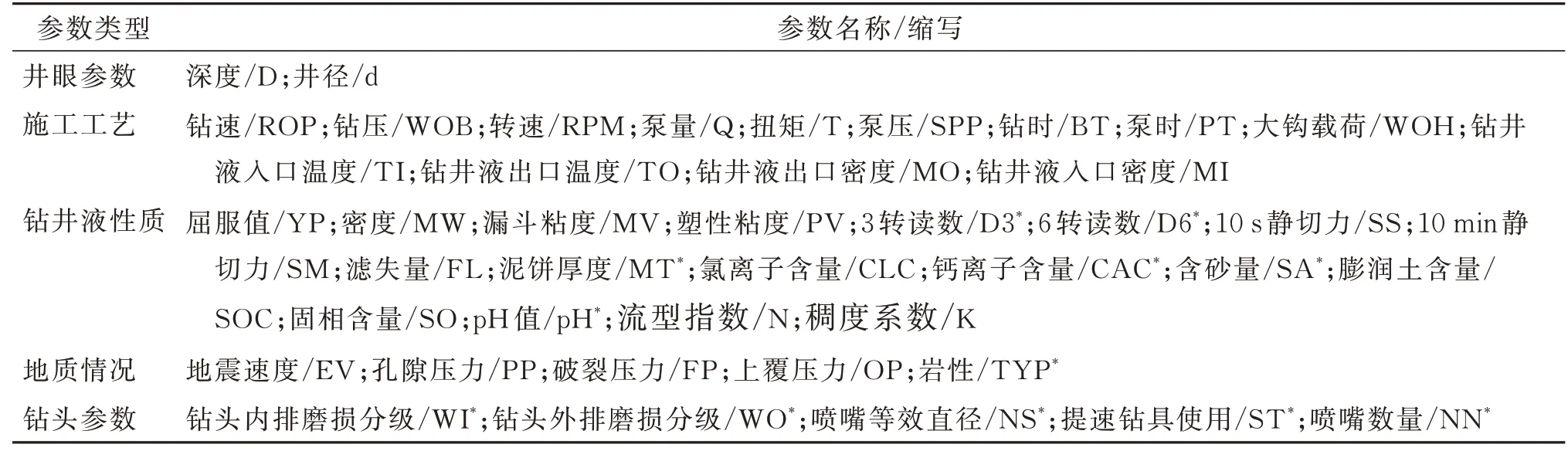
表1 参数信息Table 1 Parameter information

2.2 数据清洗

数据清洗就是指利用数据分析将采集到的“脏数据”转化为符合要求的数据［12-13］。对于钻井“脏数据”的清洗过程包括异常值的检测、删除以及缺失数据的插值补全。观察采集到的3697 条原始数据，发现前面的967 条数据中有大量参数未采集到，因此判定为无效数据，采用删除策略后剩余3000 条数据。由于所采集数据缺失部分为离散值，因此采用k 近邻填补法（KNN），即计算欧几里得空间中每个样本点与被填补点的距离，选出k 个距离最近的样本点的类别，采用投票法决定填补值，距离计算采用欧式距离，计算式如式（1）所示［14］。

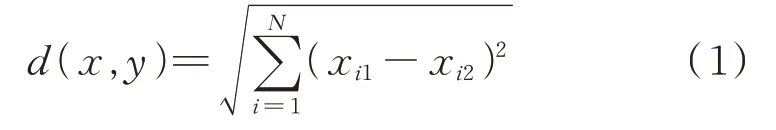
式中：d——欧式距离；N——N维空间；xi1——第1个点的第i维坐标；xi2——第2 个点的i维坐标。

2.3 数据标准化处理

补齐数据之后，由于参数数据间较大的量纲差距会给后续的机器学习建模的模型性能造成隐患，因此需要对数据做标准化处理来缩小量纲差距，其计算式如式（2）所示［15］。

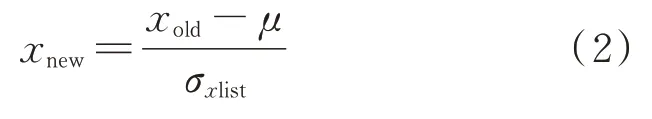
式中：xnew——完成标准化的数据；xold——标准化前的原始数据；μ——平均值；σxlist——原始数据同一变量所有数据标准差。

以钻压和钻井液出口温度为例，标准化处理之后效果展示如图2 所示。

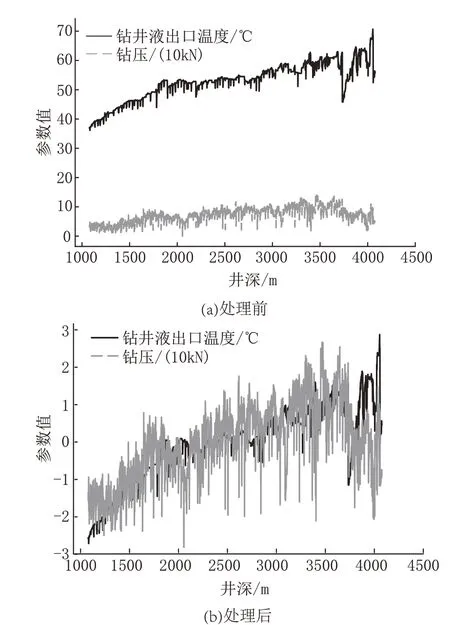
图2 标准化处理前后对比Fig.2 Comparison before and after standardization

3 融合特征选择算法设计

3.1 相关性分析

相关性分析的主要目的在于判定输入与输出变量之间的相关性以指导建模时下一步该采取何种操作，本文采用皮尔逊相关系数计算方法对所选变量进行相关性分析，筛选出高相关性参数组作为特征选择工作的第一步，计算方法如式（3）所示［16］。

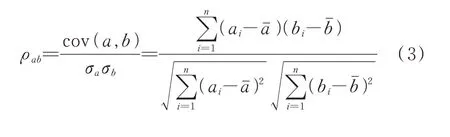
式中：ρab——a、b变量之间的相关性；cov(a，b)——变量a、b的协方差矩阵；σa、σb——变量a，b各自的标准差；ai、bi——变量a、b数据集中第i个变量值；aˉ、bˉ——变 量a、b平 均 值；n——变 量a、b的 数 据 集大小。

ρab的取值在区间［-1，1］上，取值为正时，表示两个参数之间呈现正的相关性，反之则表示两个参数呈负相关性，ρab的绝对值越靠近1，说明a、b之间的相关性越高，越靠近0，则说明两个变量之间的相关性越低，计算表1 中钻速ROP 参数与除钻速之外的所有其他参数之间的相关性，计算结果如图3、图4 所示。

图3 低、中相关性参数组Fig.3 Low and medium correlation parameter groups

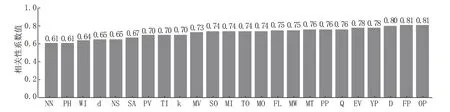
图4 高相关性参数组Fig.4 High correlation parameter group

对计算结果进行统计，可按照皮尔逊相关性系数将除钻速之外的其他参数与钻速的相关性分为高相关性、中相关性和低相关性3 类［16］。

（1）高相关性参数：总共有24 种，占所有参数的55.81%，该类参数与钻速的相关性系数计算结果的绝对值均位于［0.6，0.81］区间内。

（2）中相关性参数：总共有15 种，占所有参数的34.88%，该类参数与钻速的相关性系数计算结果的绝对值均位于［0.1，0.6］区间内。

（3）低相关性参数：总共有3 种，占所有参数的9.31%，该类参数与钻速的相关性系数计算结果的绝对值均小于0.1。

从相关性系数计算结果可以看到传统经验中如岩性等参数的相关性系数取值较低，这是因为皮尔逊相关性分析对线性相关的参数更为敏感，更容易选出线性关系更明显的特征，因此传统钻速研究中非线性相关的参数相关性系数值会相对较低。

3.2 方差过滤

在机器学习建模过程中，引入的参数相关性越高，建立高精度机器学习预测模型所需要的参数数量越少［17］。因此，使用方差过滤法选择少量的包含更多信息量的参数，以提升模型的效率和精度。其原理是对于离散型特征，对方差进行计算，然后按计算结果保留贡献较大的特征。其操作步骤是先对离散型特征参数进行方差计算，观察计算结果发现，特征方差以岩性（TYP）为界呈明显的两级分布，因此以TYP 方差2.6157 为阈值，选择方差大于和等于阈值的特征，方差计算结果如表2 所示。

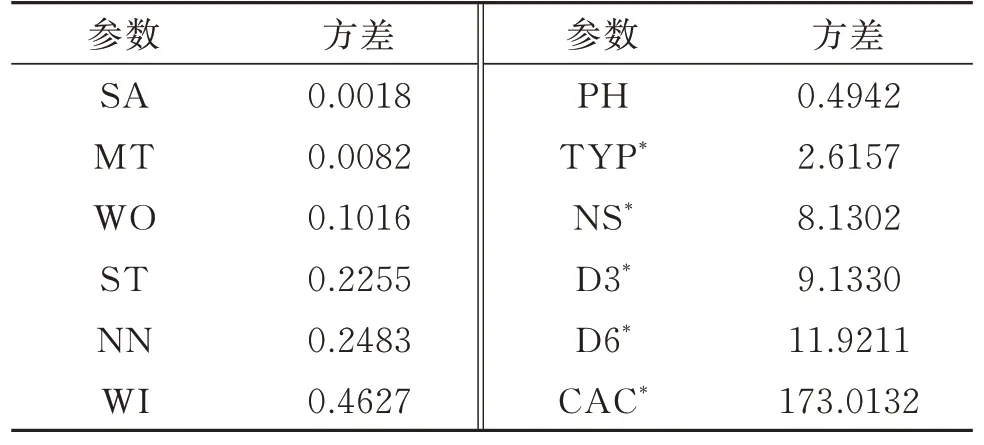
表2 离散型参数方差Table 2 Discrete parameter variance

3.3 互信息法

离散型特征选择结束之后，用互信息法从30 个连续型参数中选出特征量相对较少且互信息估量较高的参数组，互信息定义如式（4）所示，其估计量取值区间位于［0，1］，其值越大，表明变量与标签之间的相关性越大［18］。

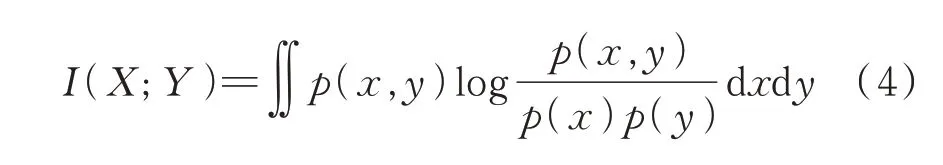
式 中：p(x，y)——X与Y的 联 合 概 率 分 布；p(x)、p(y)——边缘概率分布。

操作步骤是先对30 个连续型特征进行离散化处理，然后计算出每一个参数的互信息估计量并排序，计算结果如表3 所示，最后利用前向搜索策略结合模型后验法，即依次向模型输入特征，每输入一个特征对模型进行一次评价，当模型性能提升时则选择当前特征，当模型性能下降则过滤掉特征。前向搜索过程如图5 所示，图中折线上三角点对应参数为互信息法结合前向搜索策略选择特征参数，其余点对应参数为被过滤参数。

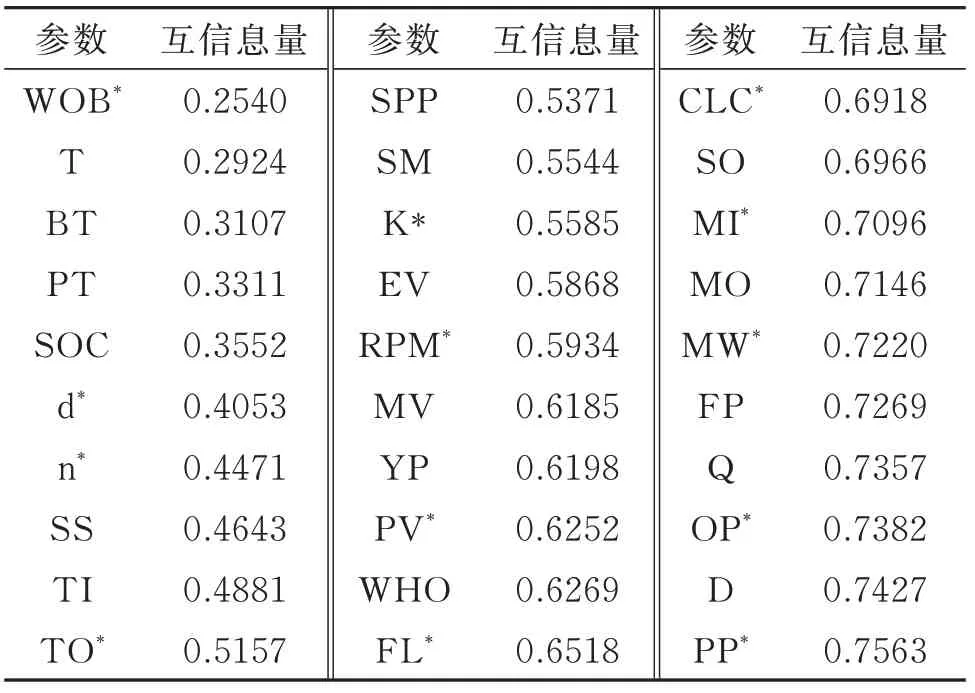
表3 互信息量估计量Table 3 Mutual information estimator

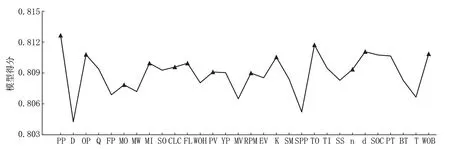
图5 基于前向搜索的互信息特征筛选Fig.5 Mutual information feature screening based on forward search

3.4 融合特征选择算法步骤及评价

融合皮尔逊相关性分析法、方差过滤法和互信息法进行特征选择，其操作步骤如图6 所示。

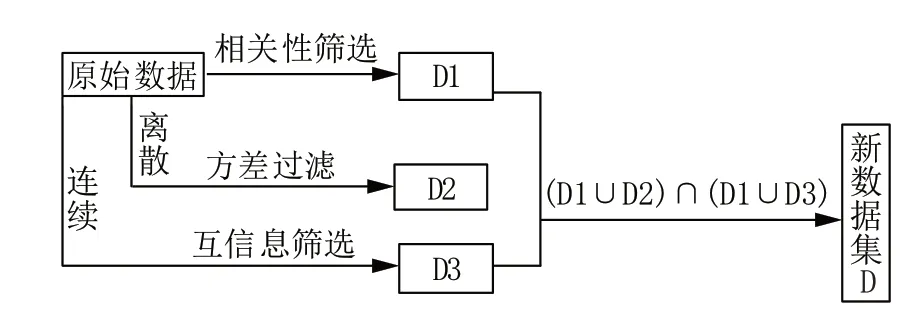
图6 特征选择过程示意Fig.6 Schematic diagram of the feature selection process

操作可分为4 步：

（1）对经清洗之后的数据进行皮尔逊相关性计算，按照皮尔逊相关性原理将所有特征参数划分为高相关性参数组、中相关性参数组和低相关性参数组，然后选择与钻速具有高相关性的高相关性参数组作为特征选择的融合算法的第一步选择；

（2）将所有特征参数中的离散类型参数按照方差过滤法原理进行方差过滤，然后选择方差值高的特征参数作为特征选择的融合算法的第二步选择；

（3）将所有特征参数中连续类型参数按照互信息法计算原理进行互信息估计量计算并按互信息估量值的大小进行排序，然后使用前向搜索策略结合模型验证来进一步进行特征筛选。

（4）将通过相关性过滤结果的参数组分别与方差过滤结果参数组和互信息过滤参数组结果分别取交集，最后将2 个交集参数组取并集作为特征选择的融合算法的最终选择结果，它们与钻速的相关性系数、方差及互信息量如表4 所示。

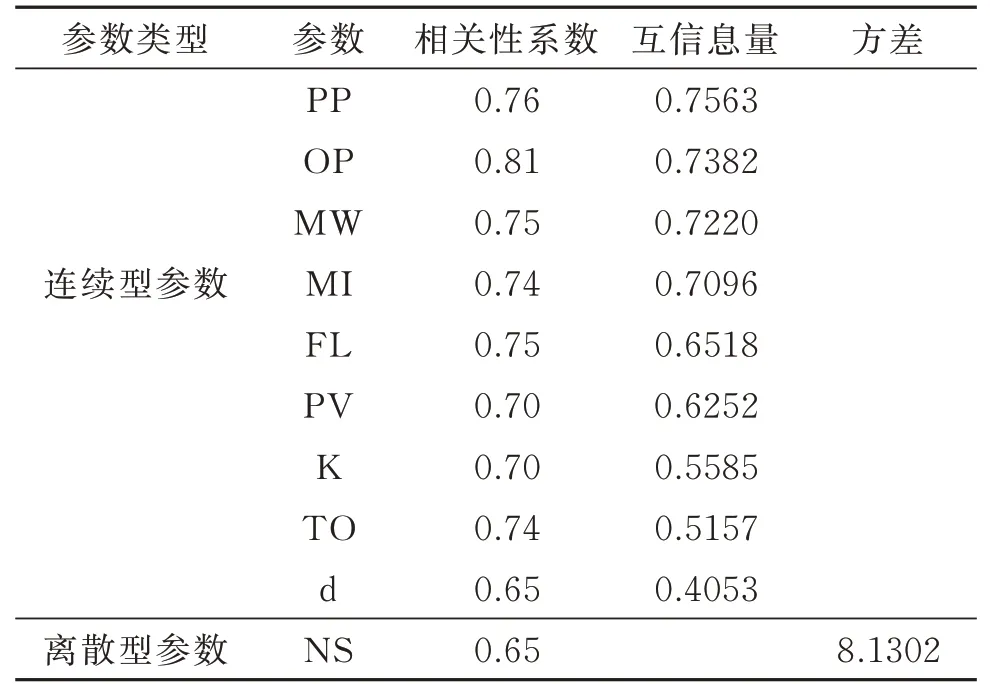
表4 融合特征选择算法特征选择结果Table 4 Feature selection results with fusion feature selection algorithm

在设计的融合特征选择算法中，利用皮尔逊相关性系数方法和方差过滤方法能够有效去除数据中的无关特征，使得模型的输入参数间会存在较大耦合。因此进行的第三步操作：将互信息法与前向搜索策略结合能够有效剔除部分相互耦合的特征。

4 基于融合特征选择结果的GBDT 钻速预测模型

4.1 GBDT 算法模型介绍

GBDT 算法属于集成学习算法的一种，它融合了装袋法（Bagging）与提升法（Boosting）的思想，由Firedman 在2001 年提出，既可用来解决分类问题，也可用来解决回归问题［19］。GBDT 算法由多个基学习器f(x)、残差构成的损失函数L(x，y)以及加法集成策略H(x)构成，其原理如图7 所示，为方便展示，图中用虚线框表示多个基学习器及其预测结果。

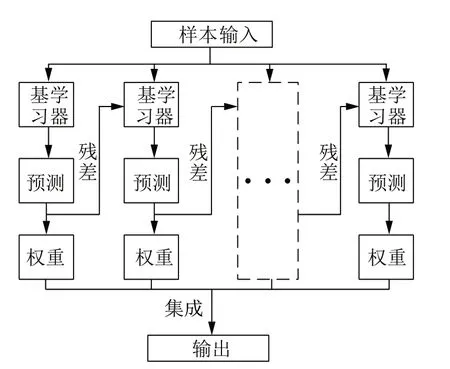
图7 GBDT 算法原理示意Fig.7 Schematic diagram of GBDT algorithm principle

GBDT 算法的基学习器由决策树组成，单棵决策树的结构越复杂，GBDT 算法的整体复杂度也会更高，使得计算缓慢且易过拟合。

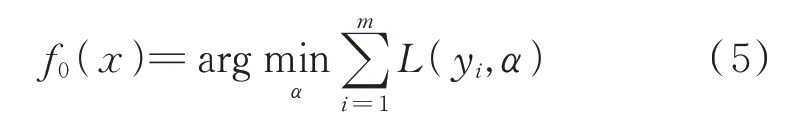
选择平方误差（squared_error）作为GBDT 算法的损失函数，因为此函数一阶导数连续，易于被优化，是一个鲁棒的损失函数，式（6）为其计算表达式：

式中：L[yi，f(xi)]——损失函数；yi、f(xi)——分别为每个样本（xi，yi)的真实值和拟合值。

在此基础上，将损失值的负梯度作为残差估计值，利用梯度提升技术对残差进行拟合：

式中：Rik——残差估计值；k——第k（k=1，2，……K）次迭代。

GBDT 算法对基学习器进行集成时遵循的原则是依据上一个基学习器fk-1(x)的结果，计算损失函数L(yi，f(xi))，并使用损失函数自适应的影响下一个基学习器fk(x)的构建，集成模型的输出结果。其操作步骤是先确定每个叶节点区域对应损失函数最小化的最佳拟合值εik，然后更新学习器fk(x)，最终构建GBDT 模型如式（8）所示［19］。

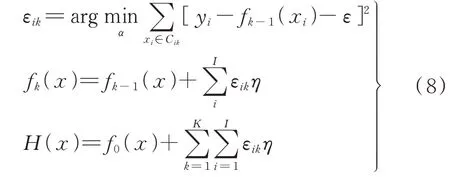
式中：η——学习率；Cik（i=1，2，……I）——得到的第k棵树的叶节点区域；εik——每个叶子点区域确定使对应损失函数最小化的最佳拟合值；H(x)——GBDT 模型最终拟合结果。

4.2 模型设计

导入经融合特征选择算法所确定的特征参数进行机器学习建模，采用10 折交叉验证法降低模型过拟合风险，使用决定系数（R2）、均方根误差（RMSE）和相对误差（MAPE）等指标对模型进行评估，部分数据展示如表5 所示。

表5 模型输入部分数据Table 5 Some model input data

4.2.1 10 折交叉验证

将数据集等比例划分成10 份，以其中的一份作为测试数据，其余9 份作为训练数据，每次试验选取不同的测试集，剩下的作为训练集，重复进行10 次试验，最后把10 次测试集得分平均作为最终得分，其原理如图8 所示［20］。

图8 10 折交叉验证原理示意Fig.8 Schematic diagram of the 10-fold cross-validation principle

4.2.2 模型评估

4.2.2.1 决定系数（R2）

决定系数是指回归直线对观测值的拟合程度，R2越接近1，表明拟合程度越好［20］。其计算式为：

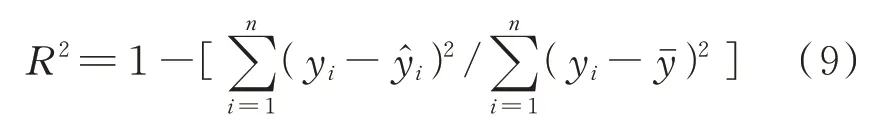
式 中：yi——真 实 值；——真 实 平 均 值；̂——预测值。

4.2.2.2 均方根误差（RMSE）和相对误差（MAPE）

均方根误差是预测值与真实值偏差的平方和的均值的平方根，其计算式如式（10）所示；相对误差是指误差与真实值的百分比，其计算式如式（11）所示，它能够表示预测值的可信程度［20］。二者均能表示预测值与真实值的偏离程度，其取值越接近于0，表示模型的性能越好，预测精度越高。

10 次试验的评分如表6 所示，R2最高能达到0.88 的预测精度，平均达到0.85 的精度。从误差的角度来看，平均均方根误差为4.57，平均相对误差为16%，表明模型预测精度较好，预测偏差较小，能够在一定程度上对机械钻速进行准确预测。

表6 GBDT 模型下10 折交叉验证试验R2Table 6 10-fold cross-validation test R2 under GBDT model

为了展示预测结果与真实值的拟合关系，提取出10 次测试集的预测值绘制回归直线拟合关系图，如图9 所示。此时R2为0.85，RMSE和MAPE分别为4.57 和16%，可以观察到所有的数据都分布在拟合线的周围，表明模型有不错的预测精度。

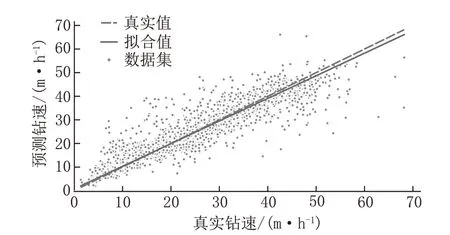
图9 GBDT 预测真实值拟合关系Fig.9 Fitting relationship between GBDT predictions and true values

取10 折交叉验证时划分为10 部分数据中的第1 部分和第2 部分测试集的预测值和真实值对比，绘制GBDT 模型预测值和真实值的关系图（图10），可以看到钻速预测值与真实值吻合，同样表明模型的拟合效果较好。

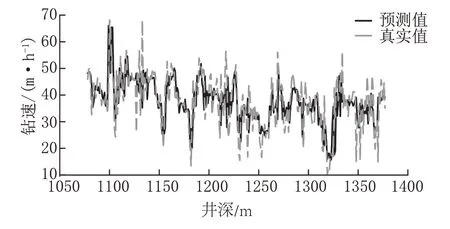
图10 钻速预测值与真实值对比Fig.10 Comparison between the predicted ROP and the actual ROP

4.3 对比试验

为验证融合特征选择算法在预测性能上的优势以及GBDT 模型相较于传统机器学习算法模型的优势，建立全特征GBDT 模型，并与特征选择结果的常用机器学习算法模型进行对比试验。

4.3.1 全特征模型

选择所有特征，使用10 折交叉验证法，建立GBDT 模型，通过比较模型在测试集上的各评估指标，发现使用全部特征作为模型输入时，模型在测试集上的泛化能力R2得分为0.83，RMSE和MAPE得分分别为4.81 和19%，融合特征选择结果建模与之相比，R2提升了2%，而RMSE和MAPE分别降低了0.24 和3%，如表7 所示。图11 为每个测试集的3个模型评估指标得分，可见经过特征选择得分均优于由全部特征所建立的模型，表明融合特征选择算法能为提高模型精度做出贡献。

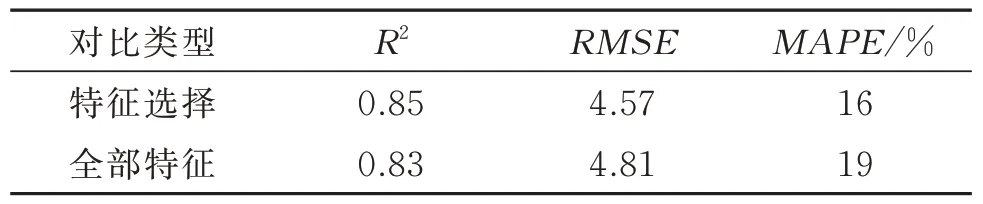
表7 模型评估指标Table 7 Model evaluation metrics

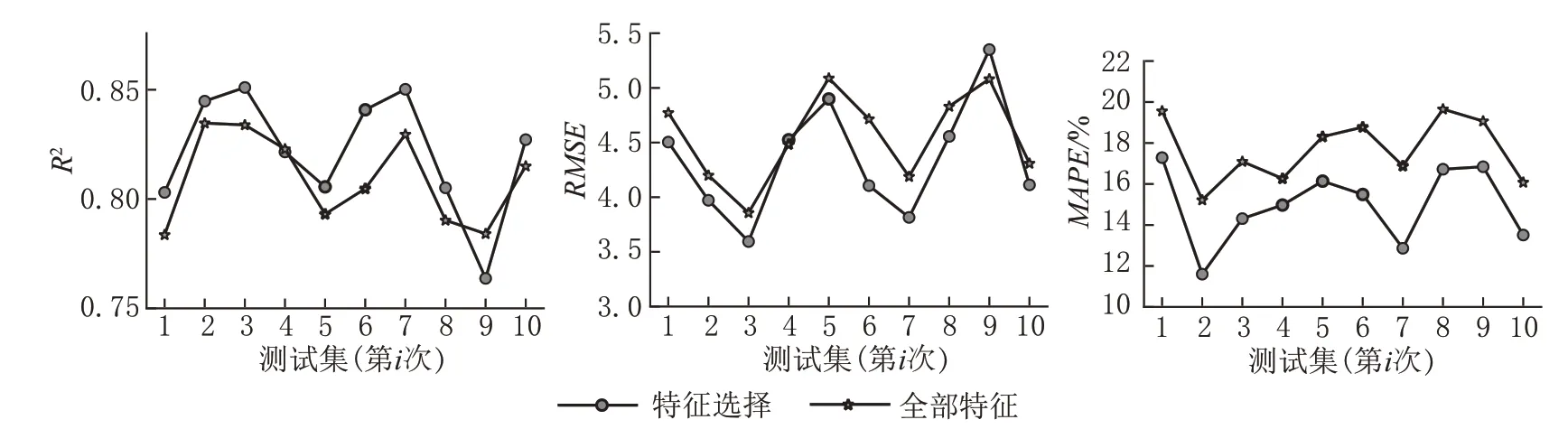
图11 全特征模型与特征选择模型测试集得分对比Fig.11 Comparison of test set scores between the full feature model and the feature selection model

4.3.2 传统机器学习模型

选择适用于高维特征计算的支持向量回归、人工神经网络中具有代表性的BP 神经网络回归、适用于处理线性关系的线性回归以及树模型的基础决策树回归算法结合10 折交叉验证进行对比试验，各模型平均得分如表8 所示，与GBDT 模型相比，GBDT 模型的R2分别比支持向量回归、BP 神经网络回归、线性回归和决策树回归高22%、18%、16%和7%，RMSE分别低了2.44、2.01、1.92 和0.85，MAPE分别低了17%、14%、13%和1%。

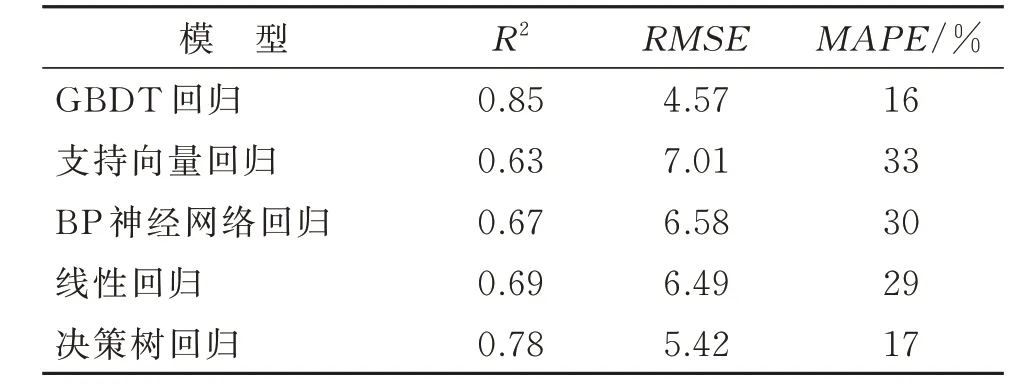
表8 不同机器学习算法模型评估平均得分Table 8 Average evaluation scores of different machine learning algorithm models

10 个测试集各模型评估指标对比如图12 所示。试验结果表明，与常用机器学习算法相比，GBDT算法模型的R2均高于常用算法模型且RMSE和MAPE均低于常用算法模型，说明在此井眼中，GBDT 模型对机械钻速的拟合效果更好，在测试集上具有更好的泛化性能。

图12 GBDT 模型与常见机器学习算法模型测试集对比Fig.12 Comparison of the test sets between the GBDT model and the common machine learning algorithm model

5 结论

准确的机械钻速预测是提高钻进效率、降低钻井成本的重要手段。本文以南海某井眼钻井数据为例，融合相关性分析、方差过滤、互信息法并结合前向搜索策略进行特征选择，然后建立GBDT 模型对机械钻速进行预测，主要结论如下：

（1）针对钻速预测机器学习建模之前特征的选择，本文提出的融合特征选择算法能够准确地从大量特征参数中选择出对模型贡献最大的参数，从而降低特征空间的维度，与使用全部特征所建立的模型相比，经过融合特征选择算法选择的特征参数所建立的模型的精度优于使用全部特征所建模型的精度，表明融合特征选择算法能够为机械钻速准确预测选择出合适的参数，且该算法能够为智能钻井机械钻速预测提供科学依据。

（2）本文所建立的梯度提升回归树模型在测试集上能够达到85%的精度，即表明模型有较好的泛化性能，能够较好地拟合机械钻速，与常用的机器学习算法相比，GBDT 算法模型的决定系数R2均高于常用算法模型，且均方根误差RMSE和相对误差MAPE均低于常用算法模型，表明GBDT 模型预测性能比传统机器学习模型更具优势，也说明GBDT模型在未知数据上具有更好的泛化能力。

（3）本文所融合的多种特征选择方法能够有效剔除数据中的无关特征，但并不能解决参数间的耦合问题，因此本文在融合的方法中结合了前向搜索策略，能够在一定程度上减少参数间的耦合。不足之处在于该算法侧重于对具有物理意义的参数进行选择，因此并没有针对最终的特征选择结果进行特征信息研究，将来的研究中可对此进一步优化。