地质钻探垂钻定向纠偏控制的工程实现与实验分析

张 典，杜 胜，陆承达，陈略峰，曹卫华，吴 敏*

（1.中国地质大学（武汉）自动化学院，湖北 武汉 430074；2.复杂系统先进控制与智能自动化湖北省重点实验室，湖北 武汉 430074；3.地球探测智能化技术教育部工程研究中心，湖北 武汉 430074）

0 引言

地质钻探是地质勘探的重要手段，其对于地质资源开采具有重要意义［1］。在地质钻探领域，由于设备、成本、钻进取心工艺以及深部地层勘查任务等原因，垂直孔往往是最佳选择，而垂直钻进作业是钻成垂直孔的重要手段［2-3］。

为获得高质量垂直孔，在垂钻作业中需保证钻进轨迹沿井口铅垂线向下延伸。由于地层倾向、岩性软硬交替、钻进设备、控制工艺以及人为等因素，在垂钻过程中容易造成钻进轨迹的偏斜［4］，垂直钻进过程定向纠偏控制是解决钻进轨迹偏斜的重要技术手段［5-6］。

目前实际工程中垂钻轨迹纠偏控制主要依靠人工经验控制井斜［7-8］。为提升纠偏效果，学者们对纠偏控制方法进行了大量研究，其中模型预测控制因其良好的工程应用效果［9-10］，近几年成为了钻进纠偏控制的研究热点。Zhao 等［11］将MPC 控制器与方位校正控制器组合以实现三维轨迹跟踪控制。Demirer 等［12］在MPC 的实际应用中取得了突破，钻探过程的控制约束在他们的工作中得到了高度重视。同时也有学者将非实时数据问题作为反馈延迟特性进行处理，从而达到控制目的。Georgiou 等［13］考虑测量延迟、参数不确定性以及在不可预知的环境中存在的干扰问题，提出了一种鲁棒模型预测控制方法，用于解决旋转导向系统轨迹跟踪控制问题。笔者也针对纠偏控制方法有丰富的理论研究成果［14-17］。

理论提出的纠偏方法需反复进行实验验证方可应用于实际工程，然而垂钻纠偏控制过程复杂，操作难度大，所需时间和资金庞大，这使得鲜有研究能够应用于实际工程。Arbatani 等［18］基于有限元与有限元和有限段方法建立计算机仿真系统，研究定向钻孔中轨迹延伸的动态过程。Tervydis 团队［19］开发了一套计算机模拟系统，用于解决非开挖水平钻进过程轨迹规划问题。现阶段有关纠偏控制的研究已较为丰富，然而其应用却十分少见，多停留在计算机仿真阶段，因此发展与研究定向纠偏控制工程实现技术十分必要。

本文以地质钻探钻进过程定向纠偏控制的工程实现为导向，首先分析并给出实际纠偏工艺过程以及纠偏控制的特点与目标；然后总结基于模型预测控制的纠偏控制问题与优化目标，结合笔者早期的一些纠偏控制理论研究，分别阐述不同纠偏工况下的纠偏控制方法；其次开发定向纠偏控制系统，用于集成纠偏控制算法，使得算法能够应用于实际工程；最后设计纠偏控制实验，以验证纠偏控制算法的工程适用性，为纠偏控制算法的工程实现迈出重要一步。

1 定向纠偏过程描述

定向纠偏主要依靠钻机系统实现，系统结构如图1 所示。其中与定向纠偏相关的主要结构包括井底钻具组合、钻杆、钻头、测量系统和井上系统。其中井上系统包括司钻滑轮、游车、转盘、主绞车和泥浆泵等，其主要用于提供钻进所需的钻压、转速与泵量。测量系统由打捞绞车和测斜仪组成，其主要用于定点测斜。

由于钻进成本和井眼口径限制，基于滑动导向的纠偏工艺仍然是现如今地质钻探领域的主流工艺，而滑动导向主要通过基于螺杆钻具的井底钻具组合实现定向钻进。如图1 所示，该井底钻具组合主要由稳定器、井下马达总成、传动轴总成、万向轴总成以及上部接头组成，负责为钻机系统提供造斜能力，可以说井底钻具组合正是定向纠偏的核心部件。

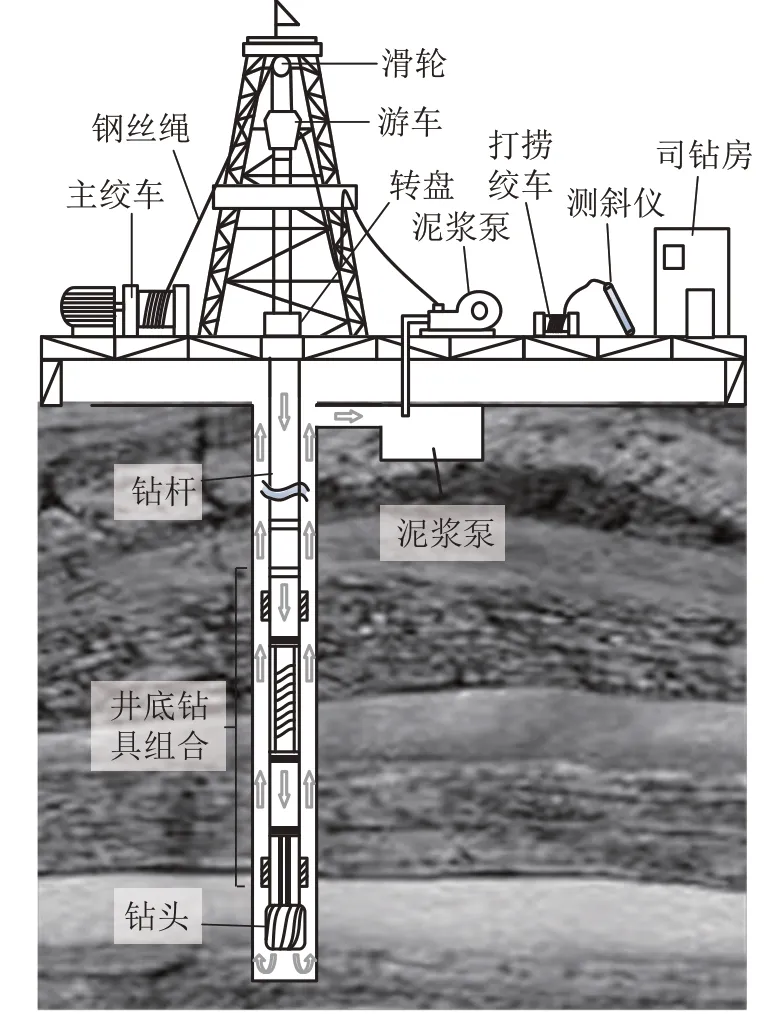
图1 定向纠偏钻进系统Fig.1 Direction drilling deviation correction system

基于上述介绍，定向纠偏过程可描述为：在钻进到一定深度时，钻进将会停止，由打捞绞车从中空钻杆内部下放测斜仪至井底，静态测量井底处的井斜角与方位角；结合历史测斜数据，可计算整条井眼轨迹，同时确定当前井底的偏斜参数；由工程师设定下一井段的纠偏控制量；启动钻进，通过转盘和井底钻具组合的配合，依据控制量实现定向造斜，钻进一定深度，再次对井下轨迹进行测斜；通过一段又一段的测斜与控制，实现垂钻轨迹的纠偏。另外纠偏的前提是系统能够实现正常的钻进，其主要通过井上系统的配合，为系统提供必要的钻进参数，即钻压、转速和泵量，从而实现正常钻进。

关于定向纠偏中定点测量的具体工艺特点描述如下：由于测斜仪的使用限制，工程中一般采用静态的方式对钻进轨迹进行测斜，即每钻一定距离停钻测斜一次，一般为1 根钻杆的长度。同时由于地层等因素影响，钻进过程中钻速并非一成不变，这也使得测斜的时间间隔并非固定。目前测斜仪测量所得井下测斜参数主要包括井眼轨迹的井斜角与方位角，井深参数由井上测量得到。将这3 个参数输入到井眼轨迹计算模型中，可获取井眼轨迹的其他参数，包括井底坐标和水平偏移等，典型的井眼轨迹计算模型为最小曲率法。

垂钻纠偏控制目标是在保证井斜角较小的同时，提高钻进轨迹的垂直精度，其中垂直精度主要通过井斜角与水平偏移来描述，水平偏移即钻进轨迹上离井口铅垂线的水平距离。另外钻进轨迹的调整主要依靠转盘与井底钻具组合的配合来实现，而操作依据的工程参量称为工具面向角与导向率，其分别对应着纠偏过程中对钻进方向与钻进曲率调整的大小。

文献［20］给出了最终的垂钻轨迹延伸模型如式（1）所示。

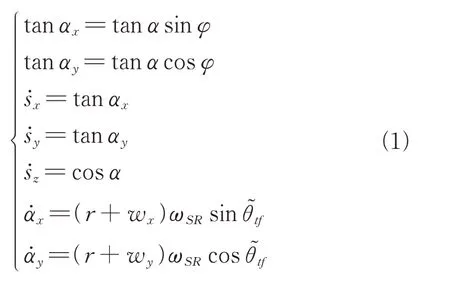
其中模型中主要用到的状态量为2 个水平偏移状态参数sx和sy以及2 个井斜角分量αx和αy。另外，sz为垂深，α为井斜角，φ为方斜角，r为额定造斜率。定向纠偏的主要过程是依据控制量工具面向角与导向率ωSR调节井底钻具组合的造斜状态，改变钻进轨迹延伸走向。

另外使用wx与wy作为2 个过程噪声，分别指2个水平方向上地层干扰对工具造斜率的影响。从文献［17］的分析可知，钻具过程中地层造成的造斜率的波动近似服从均值不为零的正态分布或者一个在尺度和幅值上调整了的伽马Γ(3，2)分布。即过程噪声可表示为如式（2）所示，其中Wk=[wx，wy]T。

其中θW为确定随机分布概率密度函数的相关参数。随着井孔深度的不断增加，井内温度与压力也开始缓缓上升，孔内环境逐渐变得恶劣，测量不可避免地具有一定噪声［21］。而垂直钻进过程中需保持较低井斜角，纠偏控制的精度往往对这种测量噪声十分敏感，因此在这种情况下，测量噪声不能被忽略。我们设定带有测量噪声的测量值如式（3）所示，其中Vk为测量噪声，其服从参数为θV的正态分布。

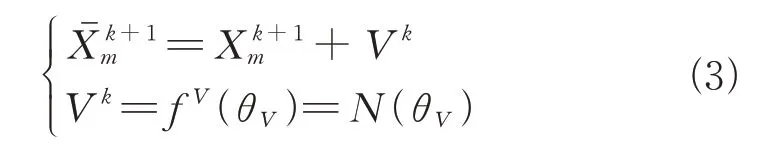
由于系统噪声可以被提前预测与整定，因此这里主要讨论测斜仪中的随机噪声。测斜仪中随机噪声主要由加速度计和磁通门传感器的热噪声以及其他环境噪声组合而成，噪声分布一般服从正态分布［22-23］。因此在这里，我们假定Vk的分布特性服从一个均值为零的正态分布。

2 垂钻纠偏模型预测控制方法

为构建基于模型预测控制的纠偏控制方法，需首先对式（1）进行离散线性化，然后构建预测方程。依据文献［15］得到离散状态空间方程如式（4）所示：

式中：sx(k)、sy(k)、αx(k)、αy(k)——第k井段处轨迹的状态量；L——定点测量的间隔井深长度；pa——离散化参数；E(μx)、E(μy)——反馈校正参数。

为了获得稳定可靠的反馈效果，设定E(μx)和E(μy)为扰动量μx和μy的幅值的数学期望，这里采用混合高斯模型（Gaussian mixture model，GMM）计算这2 个数值，计算流程如图2 所示。

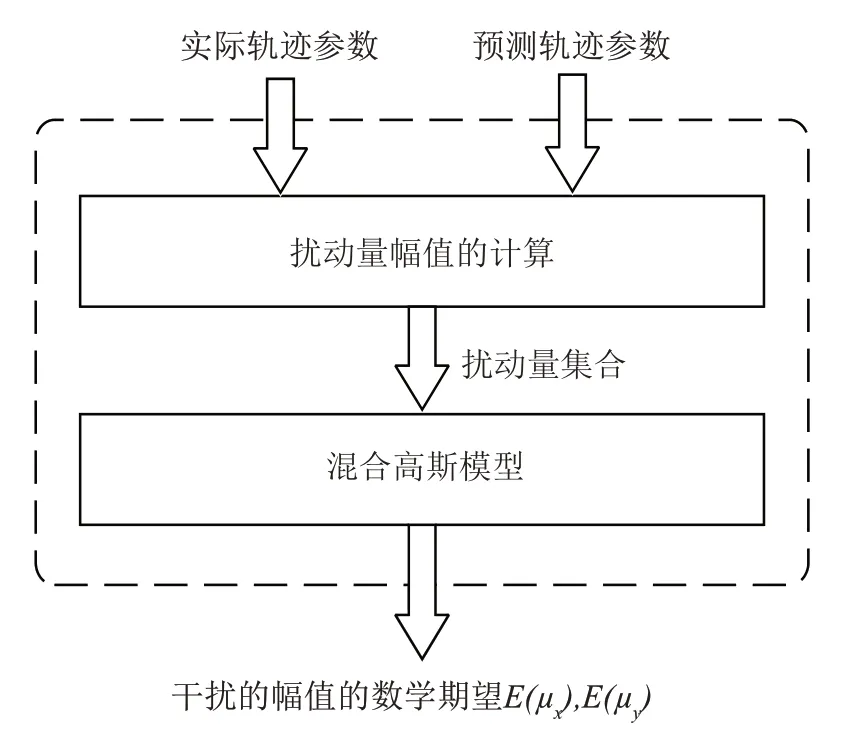
图2 基于混合高斯模型的干扰幅值期望评估Fig.2 Mathematical expectation estimation of disturbance based on GMM

依据模型预测控制理论，首先设定sx(k+1|k)指依据第k井段处轨迹的状态量sx(k)预测到的第k井段处轨迹的状态量sx(k+1)，其他状态量类似。

由定义可知sx(k|k) 与sx(k) 相等。 另外，ωx(k+1|k)指模型预测控制器在第k井段处预测用于第k+1 井段的控制量ωx(k+1)。预测方程有如下形式：

式中：x(k|k)——第k井段处轨迹的状态量，其定义为[sx(k)，αx(k)，sy(k)，αy(k)]T；Y(k)——预测值序列，其定义为[x(k+1|k)，…，x(k+p|k) ]T；U(k)—— 控制量序列，其定义为[ωx(k|k)，ωy(k|k)，…，ωx(k+c|k)，ωy(k+c|k) ]T；p——预测域长度；c——控制域长度。

将式（4）代入式（5），同时设定控制器预测域长度p与控制域长度c相等，可计算得式（5）的2 个系数矩阵为：

其中G和H矩阵分别为式（4）中的另2 个系数矩阵，G为状态系数矩阵，H为控制系数矩阵。

考虑工程约束，在垂直钻进过程中，会对井斜有一定限制，一般需保持井斜角小于一个定值αmax，因此我们的纠偏控制系统需要在保证井斜角＜αmax的情况下完成钻进轨迹的纠正。同时对于任何造斜工具，都有其造斜极限，纠偏系统需要保证所求控制量不会超过造斜工具的能力极限。结合上述分析和约束条件，针对纠偏控制系统，我们选取如下优化目标作为模型预测控制器的滚动优化目标方程：

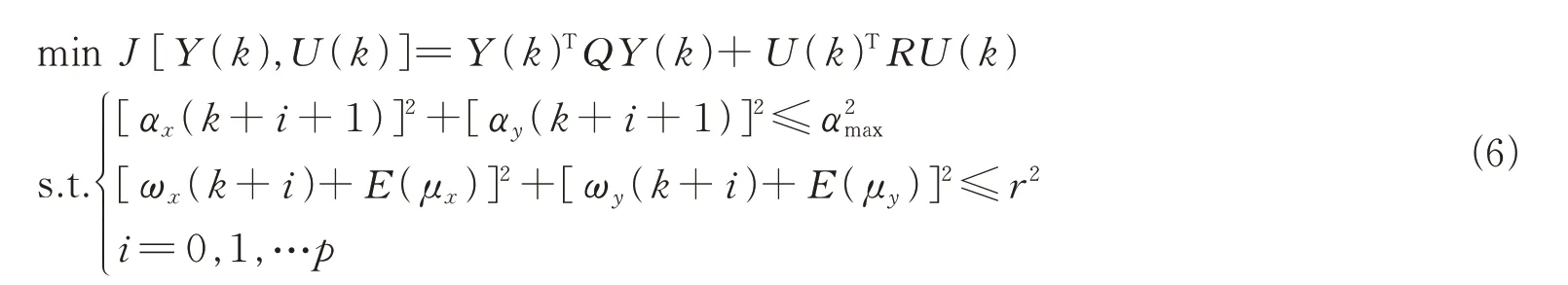
最后通过求解该优化问题，可得到最终控制序列，取序列的第一组结果作为下一井段的控制输出。

而面对存在较大测量噪声的纠偏控制问题，可设计粒子滤波器，用于实时评估估计真实状态，其定义为基于此修正离散状态空间方程如式（7）所示：

粒子滤波器设计方法由文献［17］给出。最终代入式（5）与式（6）求解纠偏控制问题，从而能够有效解决因测量噪声带来的纠偏控制问题。

3 纠偏控制方法的工业实现

3.1 纠偏控制系统硬件结构

当前主流地质勘探领域所用交流变频钻机控制系统结构如图3 所示。

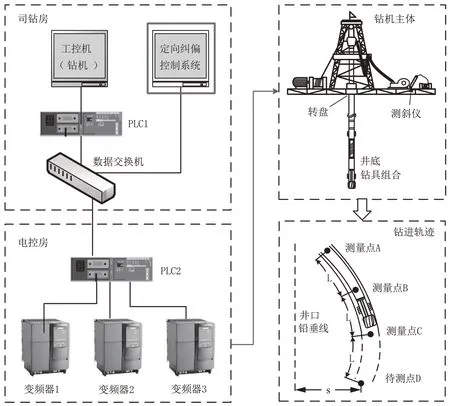
图3 钻机控制系统硬件连接示意Fig.3 Hardware structure of the semi-physical experimental system

实际钻机控制系统主要分布在司钻房与电控房之中，其中司钻房主要负责显示数据以及人机交互，电控房主要负责控制变频器和采集传感器数据。司钻房一般放置于钻机一层平台上，其中主要包括1台数据交换机、1 台工控机和1 台PLC。司钻工主要通过工控机查看钻机各项参数，同时完成钻机的基础控制，包括对转盘和井底钻具组合的综合调控。电控房中的核心器件是1 台PLC 与几台变频器，电控房中的PLC 主要通过数据线与数据交换机相连接，从而获得司钻工设定的钻机钻进参数，然后依据这些参数调节变频器输出功率。电控房中的PLC还负责采集钻机上各种传感器的测量值，综合后返送至工控机进行显示。最后，测斜仪主要通过打捞绞车进行下放与回收，测斜数据主要通过手动输入方式导入到系统内部。

为了能够增加定向纠偏控制系统的移植性，在实际应用中，我们采用新增1 台工控机的方式将我们的系统植入现有钻机系统，在不影响现有钻机系统的情况下，增设我们的纠偏控制功能，所加位置如图3 所示。纠偏控制系统通过数据线接入到数据交换机中，从而完成与原有系统的数据交互。由于现场定向纠偏工艺繁琐且复杂，定向纠偏控制系统并不直接参与钻机的控制，而是通过算法计算出合理的控制量，然后由现场司钻与工人师傅通过工控机完成后续转盘和井底钻具组合的调控。

3.2 纠偏控制软件设计

定向纠偏控制系统的软件架构如图4 所示。WinCC 负责与用户进行交互，获得用户指令与轨迹数据。核心算法由VC 实现，其中主要包括2 部分，轨迹的测算用于通过轨迹测量值测算出整条轨迹，它的核心算法包括本文构建的垂钻轨迹延伸模型以及最小曲率算法。垂钻定向纠偏控制集成本文所提三大算法，用于定向纠偏控制中控制量的计算。所有过程参数都可以保存到本地数据库，方便后续算法的评定。

图4 定向纠偏控制系统软件架构Fig.4 Software structure of the deviation correction control system

值得一提的是，定向纠偏控制系统主要通过数据点位与PLC 进行数据交互，在实际应用中，只需依照实际钻机系统中PLC 点位信息更新WinCC 的点位信息表，即可实现定向纠偏控制系统的移植，因此在实验室中所使用的系统与实际所用系统完全一致。

定向纠偏控制系统界面如图5 所示。在界面左上方，通过轨迹参数示意图显示了纠偏过程中主要的4 个参数的实际物理意义。其右面3 个部分分别通过图形化形式和数字化形式显示当前垂钻轨迹的4 个参数。界面左下方通过曲线形式显示完整纠偏过程轨迹参数的变化。其右面2 个部分为交互接口，通过测量输入部分界面可将测斜仪所得井斜角与方位角导入系统内部，通过单击纠偏计算按钮可获得下一段井段的控制量，并输出到界面右下角显示，供现场钻进工程师参看。

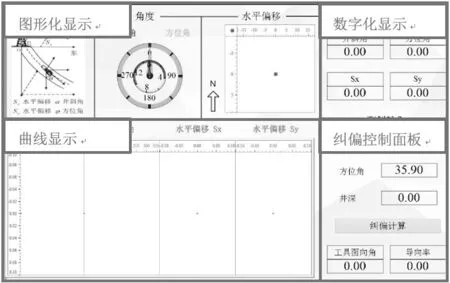
图5 定向纠偏控制系统界面Fig.5 User interface of the deviation correction control system

4 应用与实验分析

垂钻纠偏控制过程复杂，操作难度大，所需时间和资金庞大，直接将所提纠偏算法放到现场调试是不可取的。为此在实验室开发了一套控制系统与现场一致的实验平台，如图6 所示。由于其用计算机模型加实际设备相结合的方式完整模拟现场实钻过程，且其控制系统与现场完全一致，因此在此实验平台上可有效验证算法的工程适用性。

由图6 可看出，左上部分即为钻机主体与轨迹系统，其中由于室内高度限制，这里将垂钻改为了平躺钻进，并将相关参数进行了转换。轨迹系统主要设有5 个测点，用于显示最靠近井底的5 个井段。另外为了更加清晰地展现井底钻具组合的姿态，为实验平台增设了1 台三轴转台，它与轨迹系统都是通过模型计算的参数共同用于复现实际井下轨迹与钻具状态。

图6 纠偏控制半实物实验平台Fig.6 Semi-physical experimental system for deviation correction

其实验流程为：首先设定模型参数，确定模拟的钻进过程类型和干扰类型；用测斜仪测量轨迹参数，通过WinCC 界面上测量输入导入测量的轨迹参数；单击纠偏计算按钮，系统会通过相应的纠偏控制算法计算下一井段的控制量，包括导向率与工具面向角；系统根据所计算控制量与垂钻轨迹延伸模型模拟实际钻进过程，计算下一井段轨迹参数，通过实际微钻与轨迹系统复现钻孔轨迹；反复重复以上过程，直至纠偏结束。

4.1 基于混合高斯模型的垂钻纠偏模型预测控制

基于混合高斯模型的垂钻纠偏模型预测控制方法主要针对存在单一方向层偏斜干扰的垂钻轨迹纠偏控制问题，提出一套合理有效的解决方案。本实验模型的主要参数设定如下：本次实验仍然设定额定造斜率r为6°/30 m，最大轨迹井斜角约束αmax为3°左右，其中需保持钻进井斜角＜αmax。一旦超过αmax，钻进系统应优先降低井斜角，以保证钻进轨迹的质量。另外设定纠偏过程中存在单一方向地层偏斜干扰，其值服从均值非零的高斯分布，即μx，μy～N(0.001571，0.000698)。其他控制参数如文献［15］所示，实验结果在图7 给出。

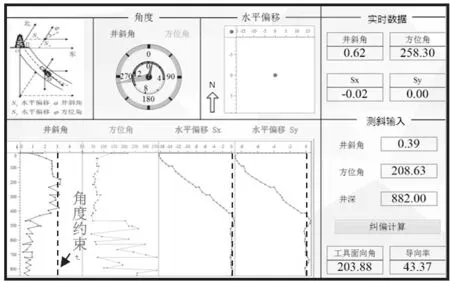
图7 基于混合高斯模型的垂钻纠偏模型预测控制Fig.7 Correction results of the model predictive control based on GMM

基于混合高斯模型的垂钻纠偏模型预测控制在水平偏移的校正方面，垂钻轨迹在500 m 处已被校正至参看轨迹附近，虽然在500 m 后轨迹由于地层干扰存在小幅波动，但轨迹并未出现较大的超调。另外井斜角也基本控制在约束范围以内，整体控制效果良好。

从应用结果可以看出，基于混合高斯模型的垂钻纠偏模型预测控制能够有效解决存在单一偏斜地层干扰下的纠偏控制问题。其主要原因是该方法并未直接将预测误差用于修正预测模型，而是通过混合高斯模型找到主要地层偏斜方向和干扰的期望值，从而获得相对稳定的反馈校正量来改善预测精度，最终获得了比较稳定的控制效果。

4.2 基于粒子滤波器的垂钻纠偏模型预测控制

本实验采用基于粒子滤波器的垂钻纠偏模型预测控制方法作为控制算法，该方法主要针对具有较大测量噪声的纠偏控制问题，提出一套合理有效的解决方案。本实验模型的主要参数设定如下：设定额定造斜率r为6°/30 m，井斜角约束αmax为3°，其中需保持钻进井斜角＜αmax。一旦超过αmax，钻进系统应优先降低井斜角，以保证钻进轨迹的质量。其他控制参数如文献［17］所示。

在半实物仿真中需要模拟存在测量噪声的垂钻纠偏控制过程，这类问题一般需要在深井高温高压环境下进行实验。而在所构建的半实物实验系统中难以复现井下高温高压环境，因此主要通过计算机将测量数据中添加1 个随机误差，该误差依据前述分析，主要服从正态分布，通过改变其均值与标准差，可以模拟不同钻进环境下的测量误差。本次实验中测量误差设定为N(0，0.64)，相较于前述仿真更大，同时设定过程噪声为0.5×(Γx-6)/6，其中Γx～Γ(3，2)。最终实验结果如图8 所示。

图8 基于粒子滤波器的垂钻纠偏模型预测控制Fig.8 Correction results of the model predictive control based on the particle flter

在基于粒子滤波器的模型预测控制纠偏控制实验中，整个纠偏过程钻进720 m，共经历90 次纠偏计算。其中可以看出水平偏差在450 m 被纠正至参考轨迹附近，但与之前实验不同的是垂钻轨迹井斜角在控制过程中波动并不大，整体变化较为平稳，最大井斜≯3.5°。另外从轨迹系统中导出的实际轨迹看出，实际轨迹的控制也较为理想，如图9 所示，实际轨迹偏差并未出现因测量不准而出现增大的情况。

图9 纠偏控制实际钻进轨迹Fig.9 Real trajectories of the deviation correction test

从上述实验可以看出，本文所提系统能够实现系统内数据的有效传递，能够清晰反映纠偏过程的各个状态和实际纠偏轨迹，清晰地显示纠偏系统的应用效果与算法优劣，总体算法使用流程符合现场工艺要求，数据交互方式符合现场实际情况，这也验证了所开发的纠偏控制系统的工程适用性。

5 结论

本文主要构建垂钻纠偏控制半实物实验平台，以便于验证纠偏控制算法的工程适用性。分析并给出实际纠偏工艺过程以及纠偏控制的特点与目标；然后总结基于模型预测控制的纠偏控制问题与优化目标，结合笔者早期的一些纠偏控制理论研究，分别阐述不同纠偏工况下的纠偏控制方法；其次开发定向纠偏控制系统，用于集成纠偏控制算法，使得算法能够应用于实际工程；最后设计纠偏控制实验，以验证纠偏控制算法的工程适用性。从实验可以看出，本文所提系统能够清晰反映纠偏过程的各个状态和实际纠偏轨迹，清晰地显示纠偏系统的应用效果与算法优劣，从而验证了所开发的纠偏控制系统的工程适用性。

下一步工作是寻找应用了定向纠偏工艺的钻进现场，将所开发定向纠偏系统安装于现场司钻房，完成定向纠偏系统的最终应用。此外，本文描述是针对x和y两维进行的，三维的分析研究将是我们今后进一步研究的工作。