Structured Controller Design for Interconnected Systems via Nonlinear Programming

Yanpeng Guan, Junpeng Du, and Xinchun Jia,,

Dear Editor,

This letter deals with the structural controller design problem of interconnected systems with unknown feedback topology. Firstly,under a cardinality constraint on the directed communication links among sub-controllers, a distributed controller’s feedback gain and feedback topology are incorporated in a unified co-design framework. Secondly, the cardinality constraint introduced in the distributed control is represented by a binary integer programming.To deal with the complementary constraint, a nonlinear programming(NLP) is proposed to relax the binary integer programming. Finally,incorporating the NLP into the standard distributed event-triggered control method, an algorithm is developed for interconnected systems to simultaneously design the feedback topology and controller gain.

An interconnected system is composed of several coupling subsystems, which usually coordinate with each other to accomplish a common task. Such systems exist in a large number of practical scenarios, such as power plants [1], intelligent transportation [2]. Due to their complex structure, large scale and comprehensive functions,interconnected systems are also referred to as large scale systems.With the rapid progress in embedded microprocessors and communication technology, a great amount of concern has been devoted to how to control the thriving interconnected systems [3].

It is noted that existing distributed control strategies are mainly claimed over prescribed feedback topologies. In this way, since the distributed controller design and the feedback topology design are mutually independent, the following two unexpected cases may emerge. On the one hand, the preset feedback topology may provide redundant communication channels, which could lead to unnecessary expenditure and malicious attacks. On the other hand, it is also perhaps that the preset feedback topology could not support the required control performance, which leaves the issue of distributed controller design unsolvable. While a feasible solution can be obtained with a minor modification of the feedback topology.Therefore, one promising way to deal with the challenge is to codesign of the feedback topology and feedback gain for an interconnected system, which is the motivation of this letter.

The overall controller gain of an interconnected system is usually a matrix with zero blocks, where each matrix block represents a channel gain and a null block implies no channel is set. Therefore,for an interconnected system, the design of a structured controller with unknown zero/nonzero structure is actually a co-design of feedback topology and feedback gain. With given controller structure, a chordal decomposition method is proposed to design sparse structured controller gain [4]. A structured controller design method is developed via constraining some decision matrix variables in the Lyapunov method [5]. In the case when feedback topology is not preset, the structured controller design problem becomes nondeterministic polynomial (NP) hard due to its combinatorial property[6]. By decomposing a nonlinear term existed in a linear matrix inequality into linear ones, a sparse promoting algorithm is presented for a liner system [7]. But a clear relationship between the sparse structure and feedback topology is not established. A alternating direction multipliers method is developed for the sake of generating a feedback gain with as many zero elements as possible in an optimal control problem [8]. A weightedl1iterative algorithm is proposed for interconnected systems to generate controller gains with null blocks[9]. More recently, a structured controller design method is proposed in [10] through a regularized mixed-integer programming (RMIP). It is noted that the method in [10] is one-step with a fixed sparsity,while iterative procedures are utilized in [9] to gradually promote sparsity in controller gain. However, one drawback of the former approach [10] is that a sufficient large upper bound should be preset for the expected structured controller gain in advance.

On the other hand, event-triggered transmission strategy (ETS) has witnessed incredible developments over the past decade due to its advantage on resource saving [11]. In effect, the way that ETS savs resources by reducing redundant transmissions, is exactly a sparsification of feedback traffic flow in some specific channel(s).While it is obvious that sparsification of feedback topology could save the transmission resources by reducing redundant feedback communication channels, which is also an important motivation of structure controller design.

This letter is going to investigate the issue of structured controller design for event-triggered interconnected systems via NLP. The main contributions of this letter are: 1) An algorithm based on NLP is developed to deal with the NP hard cardinality constraint. Compared withl1iterative algorithms, the initial point is not required to set beforehand; Compared with RMIP, the preset bound for controller gain is no longer needed. 2) A practicable solution is provided to codesign of feedback topology and feedback gain for event-triggered interconnected systems. And the limited transmission resources can be substantially saved from reducing redundant feedback channels as well as from reducing unnecessary transmissions in the remaining feedback channels.

Problem statement:Consider an interconnected system that is comprised of some coupling subsystems with the model of

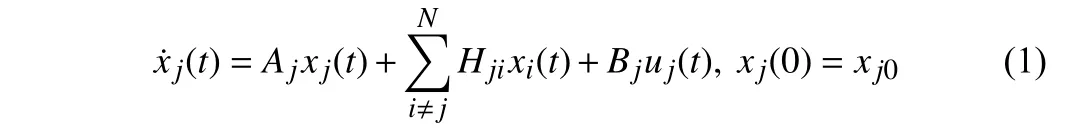
wherej∈:={1,2,...,N},xj(t) denote the state vector;uj(t)represent control input generated via sub-controllerj;A jandBjare known matrices;Hjiis a constant matrix representing a coupling gain from subsystemitoj. Fig. 1 schematically illustrates the considered interconnected system.

Each subsystem is equipped with a sub-controller, which could interact with other sub-controllers over networks. The controller for the overall system is composed ofNsub-controllers, and the form of each is given as follows:

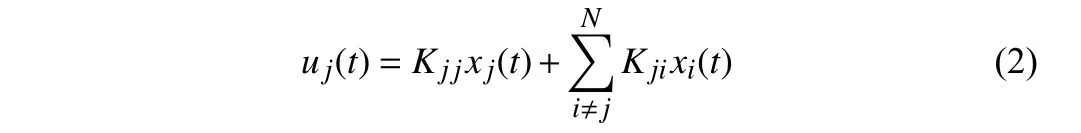
where the sub-controller gainsKjis are to be determined.

It is noted that the zero/nonzero structure ofK jisconstitutes the communication topology among sub-controllers. Different from most of the existing system frameworks [12], the communication topology among sub-controllers is neither fixed nor stochastically varying in this letter, while it is to be determined under a cardinality constraint on the directed transmission links among sub-controllers.

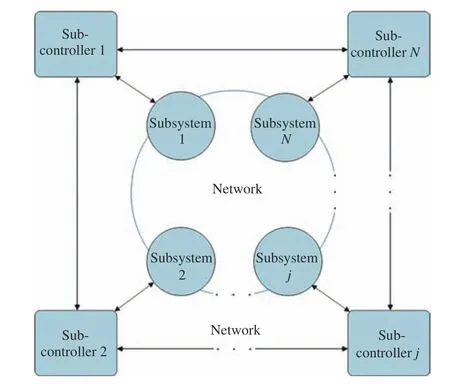
Fig. 1. A networked interconnected system.

For the purpose of reducing occupation of the transmission resources, we utilize a distributed ETS (DETS) for the transmission of state measurement. An event threshold condition of sampled data is required to be evaluated before transmission. The DETS designed in this letter will only transmit data when the threshold is violated.

In what follows,xj(kh) represents the signal sampled at instantkh.Only thexj(kh) that violates the following threshold condition will be transmitted to sub-controllerj:

It is noted that controller gain K as well as its structure is to be designed in this letter. In the existing literature on controller design of interconnected systems, the communication topology among the sub-controllers is well set beforehand. But it is practically difficult to determine which sub-controllers should be connected in advance. For the sake of seeking some optimal control performance, it is nature to set as many feedback channels as possible. However, in this way, in addition to the waste of transmission resources to some extent, the establishment of too many communication channels can also easily incur network attacks [13]. Therefore, in this letter, we constrain the number of feedback communication channels among sub-controllers prior to the design of controller gains. This number is denoted as cardnd(K)with the following definition:

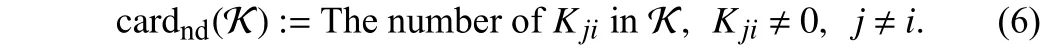
Controller (5) with cardnd(K)≤κ will be termed aϰ-sparse structured controller, where κ ∈[0,N2−N) is an integer. Therefore,our purpose is to design a structured controller gain K which guarantees exponentially asymptotical stability of the following controlled system:

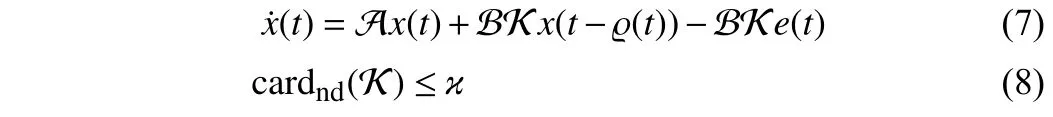
where A and B can be easily obtained from (1).

Remark 1: In the proposed system framework, to design aϰ-sparse structured controller for the interconnected system is actually a kind of co-design of feedback topology structure and the feedback gain for the system. Although the positive integerϰis preset in this letter, it can be adjusted according to practical control and/or communication requirements. Generally, a largerϰimplies more feedback channels,better control performance and higher communication cost.Therefore, one purpose of structural controller design is to seek a tradeoff between control and communication performances.

Remark 2: It is noted that all the subsystems inherit the same sampling rate in this letter. However, the developed approach applies to the multi-rate sampling scenario, where the issues of transmission delays and packet dropouts could also be considered.

Structured controller design:It is noted that the main challenge of designing a allowable controller for event-triggered closed-loop systems (7)-(8) is how to deal with the cardinality constraint (8). We will first seek a centralized feedback gain for system (7), based on which, aϰ-sparse structured controller is to be designed.

Theorem 1: With preset DETS(h,Γ,δ ), controller gain K and a positive scalarα, event-triggered system (7) is exponentially asymptotically stable, if one could find matricesX>0,Y>0,Z,Ssuch that

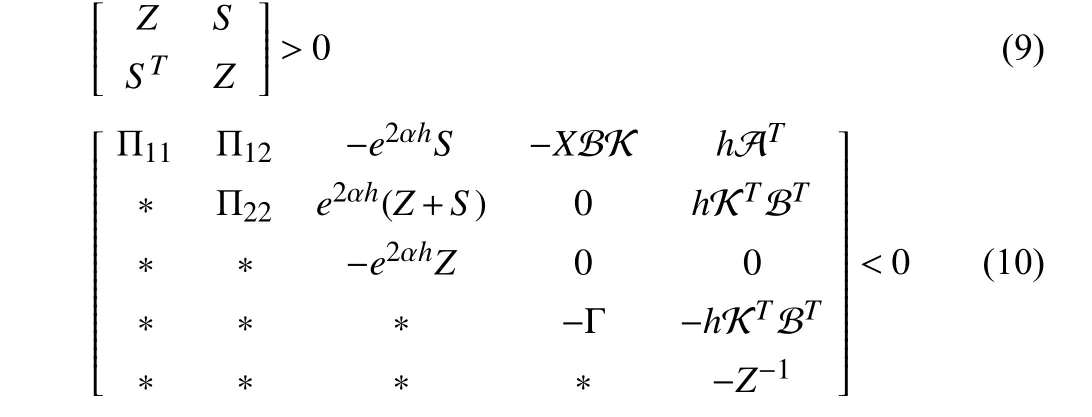
where

where

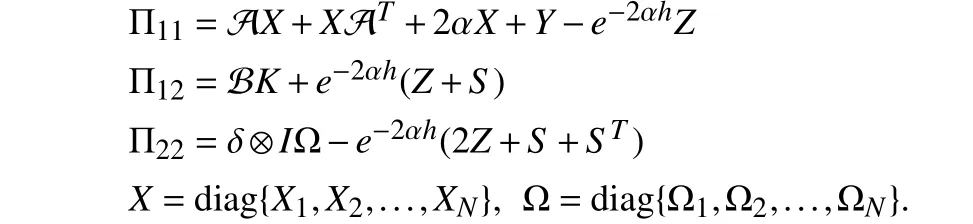
Furthermore, a centralized controller gain is given as Kc=KX−1.And the weighting matrix is given as Γ =X−1ΩX−1.

One can see that a feasible gain matrix Kcresulted from Theorem 2 does not inherit the required sparse structure. That is, the cardinality constraint cardnd(Kc)≤κ can not be guaranteed. However, from the way that Kcis generated, Kc=KX−1, one can find that cardnd(Kc)=cardnd(K)since invertible matrixXis block diagonal.Therefore, we can transfer the imposed cardinality constraint equivalently from KctoK. For this purpose, one can first partitionKinto blocks such thatKand K inherit the same block structure.Introduce a set of binary variables as follows:

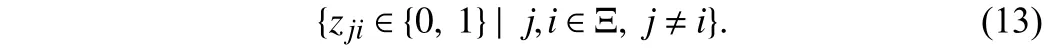
Then, the constraint c ardnd(K)≤κ can be equivalently transformed as

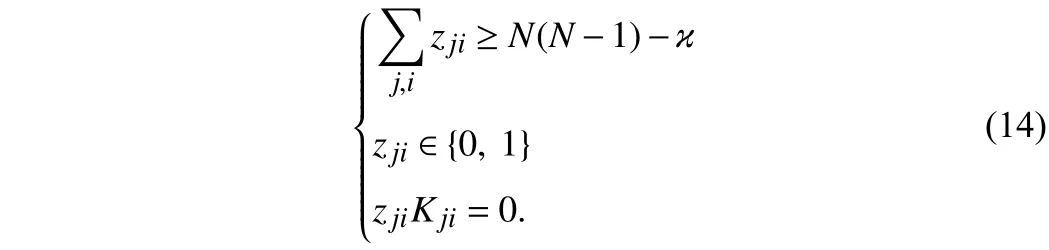
To enlarge the feasible region of binary integer programming (14),we consider a relaxation of (14).

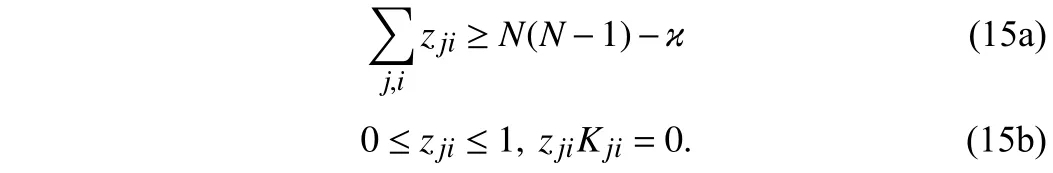
It is noted that (15a) and (15b) still can not be directly applied into structured controller design due to the complementary constraintzjiKji=0.

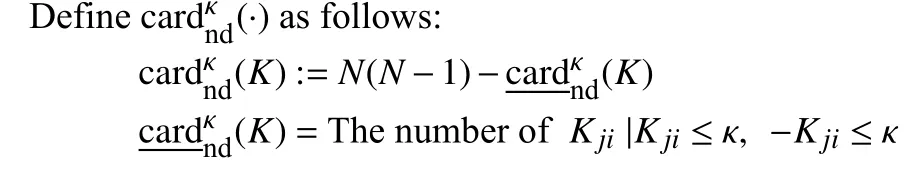
wherej≠i,K ji≤κ means that all the elements in matrixK jiare less than or equal toκwithκbeing a positive scalar. Then, we have the following result.

Lemma 1: Given a scalarκ, constraint(K)≤κ is satisfied if and only if one could find matricesK jiand scalarsz ji,j,i∈Ξ,j≠isuch that

Then, one can verify that (16a)−(16d) hold.

Sufficient condition. It follows from conditions (16a) and (16b)that the number ofz jisatisfyingz ji>κ is at leastN(N−1)−κ.Therefore, conditions (16c) and (16d) lead to(K)≥N(N−1)−κ, which implies that c ardκnd(K)≤κ holds. ■

By using Lemma 1, we can relax complementary constraint (15b)to nonlinear constraint (16b)−(16d), which can be easily resolved.Fig. 2 illustrates the feasible region of (16b)−(16d) in the scalar case,i.e., all of the matricesK jis are scalars. One can find from the figure that the feasible region of (16b)−(16d) can be described by some nonlinear functions [15].

It follows the definition that(K) denotes the number ofK’s nondiagonal blocks whose elements can only vary between [−κ,κ].Therefore, asκapproaches 0,(K) approaches cardnd(K).Based on the NLP, we have the following Algorithm 1 to generate a feasible structured controller gain K with cardnd(K)≤κ, which guarantees exponentially asymptotical stability of event-triggered system (7).

Remark 3: The values ofz jiandK jiare mutually constrained in binary integer programming (14) as well as in the nonlinear programming in Algorithm 1. In this case, the number of null or“small” blocks (K ji) can be constrained by constraining the sum ofz jis.

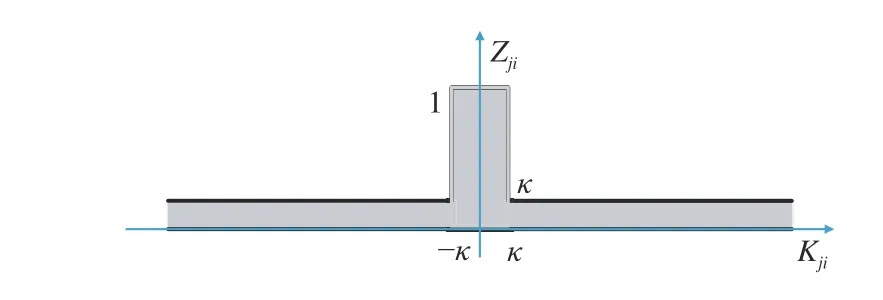
Fig. 2. Feasible region of (16b)−(16d) in the scalar case.

Remark 4: In Algorithm 1, the step length can take a larger value.For example, take κ=κ/10 in Step 4. After all, a smallerκimplies that the deleted block matrices are closer to a null matrix, and the verification in Step 4 is more likely to succeed. Or actually, one may directly obtain a feasible solution by taking a smaller enoughκonce and for all.

Algorithm 1ϰ-Sparse Structured Controller Design via NLP

An example:We select a fourth-order power plant for simulation to validate the presented structured controller design approach. The power system consists of three subsystems. The modeling and parameters of the power plant can be found in [16].

Chooseh=10 ms, α=0.01, δ=diag{0.1,0.2,0.1}. We takeκ=2 and κ0=0.01 in this example. Solving Algorithm 1 leads to a feasible K as follows:

with

In order to show the merits of the developed approach, we try to use some existing methods for sparsity optimization for the same power system, such as alternating direction method of multipliers(ADMM) in [8]. The ADMM is a typical sparsity promoting method in the literature. For the same example, the simulation results show that our nonlinear programming method can generate more zero blocks in the controller gain K in the limit case. Moreover,cardnd(K)can be easily adjustable with the developed approach.

State responses of the controlled plant shows the exponential stability of the plant. Figs. 3−5 illustrate state responses of the controlled plant. Under the DETS. It is noted that within the simulation periodTs=6 s, the number of event-triggered transmissions in the three subsystems are respectively, 130, 135, and 136,all far less than 600, the numbers of transmissions under the periodic sampling/transmission strategy. This illustrates DETS’s merit on resource efficiency.

Conclusions:The design of structured controller with sparse gain matrix for interconnected systems has been studied. The distributed control framework of an interconnected system under a DETS and unknown feedback topology has been developed for simultaneously designing of the feedback topology and feedback gain. The cardinality constraint involved in the structured controller design issue has been relaxed and resolved by a nonlinear programming. By incorporating the NLP into the standard centralized controller design method, an algorithm has been developed for designing sparse structured controller with cardinality constraint. The developed approach has been verified via a three machine interconnected power plant.

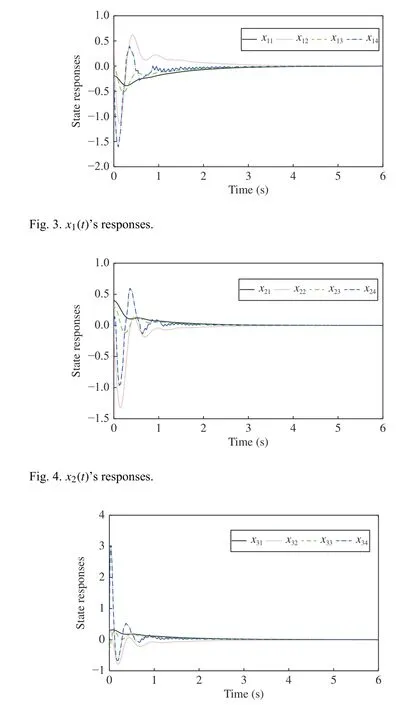
Fig. 5. x 3(t)’s responses.

Acknowledgments:This work was supported by the National Natural Science Foundation of China (61973201), and the Fundamental Research Program of Shanxi Province (20210302124030).