Collision and Deadlock Avoidance in Multi-Robot Systems Based on Glued Nodes
Zichao Xing, Xinyu Chen, Xingkai Wang, Weimin Wu,,, and Ruifen Hu
Dear editor,
In this letter, we would like to discuss a method to avoid collisions and deadlocks in multi-robot systems based on a new concept of glued nodes.
In terms of collision and deadlock avoidance, many methods are based on zone control which has two disadvantages. First, unless all nodes are collision-free, the roadmap must be divided into disjoint zones, which increases the difficulty of applying the methods.Moreover, each zone should be able to accommodate a robot, which leads to imprecision and waste of space. This letter proposes the concept of glued nodes, which can dynamically determine the mutual influence between nodes based on the real-time sizes and paths of the robots. Based on the glued nodes, this letter proposes a collision and deadlock avoidance algorithm, which can be applied to multi-robot systems with variable-sized robots and roadmaps with any structure.The experimental results indicate that the method proposed in this letter is effective and efficient.
Introduction:Multi-robot systems have been studied to apply in many areas to help people perform dangerous and tedious tasks, such as environmental monitoring, disaster rescue, and minefield mapping. As a main content of motion coordination, collision and deadlock avoidance is receiving increasing attention.
In multi-robot systems, collisions damage the robots and cause losses, while deadlocks cause the system stagnation until the deadlocks are solved manually or automatically. In industrial environments like workshops and container terminals, the roads on which robots can travel are usually planned in advance. These roads make up a roadmap, wherein an edge represents a road or part of a road, and a node represents an intersection or a point on the road.However, the compact design of some roadmaps means that two nodes are not necessarily collision-free for two robots. Especially when robots are variable-sized, i.e., the sizes of the robots are different before and after loading, two nodes are collision-free for two robots when the robots are not loaded, and they are not collisionfree when both robots are loaded. That is, whether two nodes are collision-free for two robots depends on the structure of the roadmap and the size of the robots.
The arbitrariness of the roadmap structure and the variable-sized robots bring difficulties to collision and deadlock avoidance in multirobot systems. However, the dynamic nature of the glue nodes can solve this problem. Besides, the dynamic nature makes the collision and deadlock avoidance method proposed in this latter more adaptable and more accurate than those methods based on zone control [1]−[5].
Related work:Significant studies have been devoted to addressing the collision and deadlock avoidance problem in recent years. The essence of collision avoidance is to prevent several robots from appearing in the same space at the same time. There are generally two ways to avoid collisions, one is the coupling method, which statically or dynamically plans collision-free paths or trajectories for robots, such as state lattice, reciprocal collision avoidance [6], etc.The other is the decoupling method, which decouples path planning and motion coordination. The method first plans paths for the robots with a certain goal (such as the shortest distance, least congestion,etc.), and then solves the collision problem based on the existing paths. Wanget al. [7] set different initial delays for different robots to avoid collisions. However, this type of method is time sensitive and not robust. In [8], the authors propose a petri-net controller to avoid collisions for automated guided vehicles based on zone control.
It is not enough that robots can move without collisions in multirobot systems because deadlocks will cause partial or complete stagnation of the system. There are three major approaches for deadlock handling in multi-robot systems: deadlock detection and resolution, deadlock prevention and deadlock avoidance [9].
As an online method, deadlock avoidance has been the focus of numerous studies. In [1], the authors give a limit that robots can only stop on arcs, each arc represents a zone. If a robot can find an intermediate position that is not occupied by the paths of other robots, it can move to this intermediate position to avoid deadlocks.Zhouet al. [2] model robot motion through labeled transition systems, and design a distributed algorithm to avoid deadlocks. The method is based on fixed path scenarios, where all the paths of robots are fixed. In [3], the authors divide the transport road network into non-overlapping zones and introduce a structural online control policy which guarantees that the execution of an elementary transport operation does not lead to deadlock. Malopolski [4] proposes a deadlock avoidance method based on chains of reservations, which is suitable for transportation systems with square structures. In [5], the authors propose a spare zone based hierarchical motion coordination algorithm to avoid deadlocks by locally adjusting the paths of robots.
Although these methods are effective in some scenarios, they explicitly or implicitly divide the environment into several disjoint zones, which reduces the adaptability of the methods.
Contributions:1) This letter proposes the concept of glued nodes,based on which, a novel method is proposed to avoid collisions and deadlocks in multi-robot systems. 2) The proposed method can avoid collisions and deadlocks for heterogeneous robots and variable-sized robots in a roadmap with any structure.
Problem statement:In a multi-robot system based on a roadmap,motion coordination is the process of nodes allocation in the roadmap. There is a control center responsible for the assignment of nodes, and each robot applies to the control center for nodes in real time. Only nodes which do not cause collisions and deadlocks can be authorized to the robot and become its occupied nodes.
Let N ={1,2,...,N} be the index of robots,Nis the number of the robots.RNdenotes all robots in the system andRi,i∈N denotes a robot inRN. The roadmap in the system is denoted asG=(V,E).Vm,m∈M denotes a node where a robot can reach and stop,M={1,2,...,M} is the index of nodes.Em,n=(Vm,Vn) denotes an edge betweenVmandVn,Em,nandEn,mare not the same edge.These edges can be unidirectional or bidirectional.
Problem: Given a multi-robot system with a roadmap, find an online control method to avoid collisions and deadlocks during the movement of robots.
Glued nodes:This section gives definitions related to the glued nodes.The path ofRiis denoted asPi={V1,E1,2,...,Ek−1,k,Vk}. As shown in Fig. 1,P1={V1,E1,2,V2,E2,3,V3,E3,4,V4,E4,8,V8} denotes the path ofR1. Although the paths of the two robots are not intersect atV2, they may collide with each other whenR1reachV2andR2reachV3.
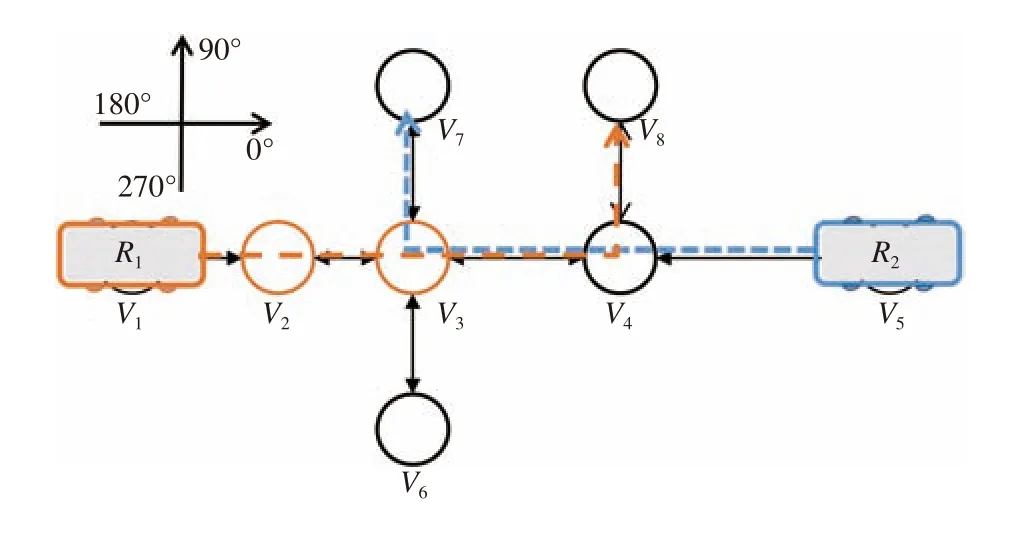
Fig. 1. An example of the robots and their paths, V 2 is authorized to R 1.

Proposed algorithm: Based on the concept of glued nodes, this section presents the collision and deadlock avoidance algorithm.
The applying nodes and occupied nodes of a robotRiare respectively denoted asAViandOVi. Once a node is occupied by a robot, the robot can move to this node along the path. Therefore,when a robot applies to the control center for a node, it needs to determine whether the authorization of the node to the robot will cause collisions or deadlocks.
Algorithm 1Collision Avoidance:CA(Ri,AVi)

Theorem 1: For ∀Vm∈OViand ∀Vn∈OVj, ifOVi∩OVj=∅ and=0 , thenRiandR jare collision-free.
Proof: There are only two types of collision in a roadmap: collision on the same node, collision not on the same node.OVi∩OVj=∅means a node will not be occupied byRiandRjat the same time, so it is impossible for two robots to appear at the same node at the same time and collide with each other. If=0, there is no overlap in the areas swept byRiandR jwhen performingandsoRiwill not collide withR j. ■
Om=RidenotesVmis authorized toRi. Based on Theorem 1, the collision avoidance algorithm is shown in Algorithm 1.AViis the nodes applied byRi, and each node is checked in turn. If a node is already occupied by other robots, the node cannot be authorized(Lines 3 and 4). Furthermore, if a node is a pair of glued nodes with another node that have been authorized to other robots, it cannot be authorized to the robot (Lines 5−9). Line 11 returns the nodes that can be authorized toRi. The complexity of the algorithm isO(NHK),in whichNis the number of robots,HandKare the maximum number of nodes in the applying nodes and occupied nodes of the robots, respectively.
However, these collision-free nodes are not necessarily deadlockfree. A deadlock avoidance method needs to be designed to avoid deadlocks among robots.

Definition 7 (conflict circle): A conflict circle is a sequence of conflict occupation like (R1→Φ1,2,R2→Φ2,3,...,Rn→Φn,1).
Theorem 2: There is no deadlock if there is no conflict circle.
Proof: According to Definitions 4 and 5, a conflict area is actually a common space swept by two robots. Once a robot occupies a conflict area, it may induce another robot to avoid collisions and stop. A conflict circle means a circular avoidance may take place. If multiple robots do not form a conflict circle, then at least one of these robots can move without being blocked, and a deadlock can not occur. ■
When the nodes occupied by the robots change, the conflict areas and area occupations will be automatically updated. The collision and deadlock avoidance algorithm is shown in Algorithm 2.
Algorithm 2Collision and Deadlock Avoidance:CDA(Ri,AVi)

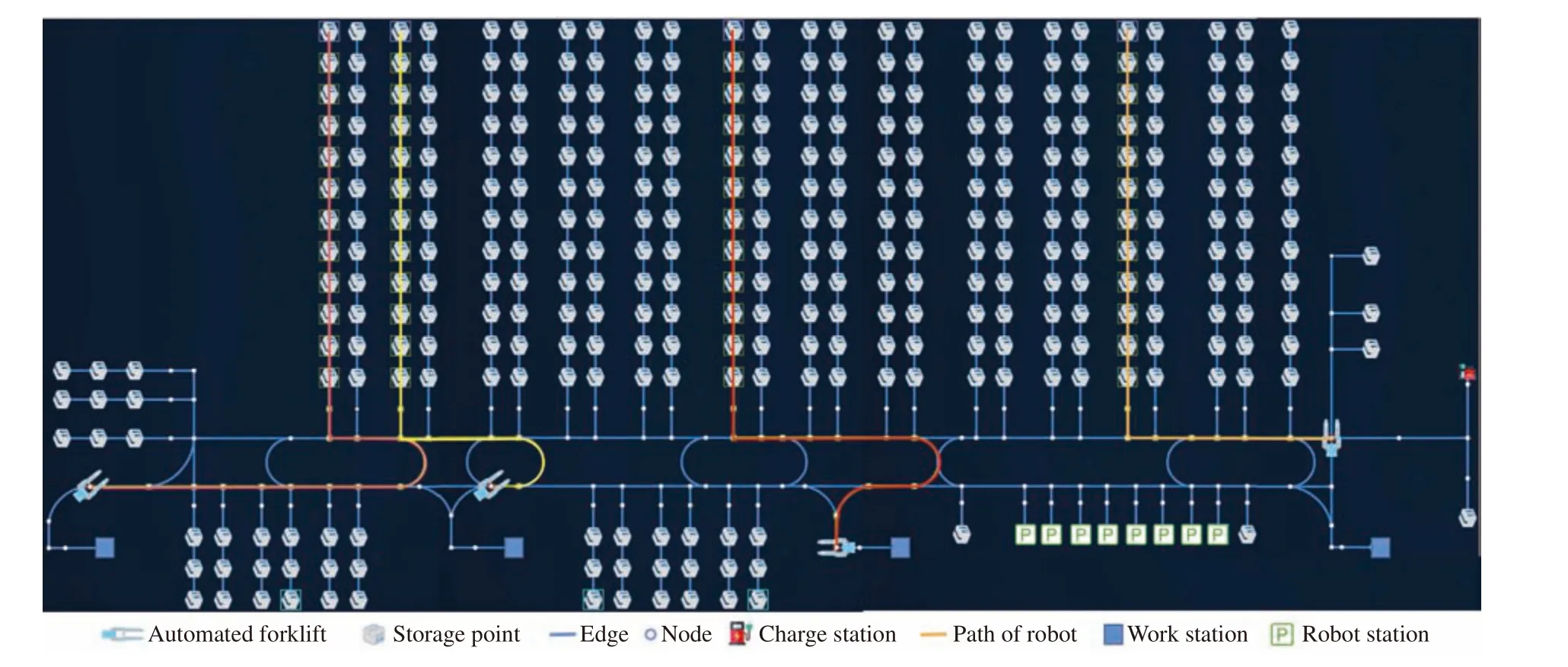
Fig. 2. Simulation in an automated warehousing scenario.
Line 2 calls Algorithm 1 to obtain collision-free nodes, and then the algorithm judges whether these nodes are deadlock-free. Lines 3−14 search for the farthest node among these nodes that is not in conflict areas, and the robot can move to this node without deadlock.Lines 16−22 judge whether the authorized nodes form a conflict circle, and only those nodes that do not form a conflict circle can be occupied by the robot. In the worst case, all nodes are in conflict areas. Therefore, in Lines 6 and 16, the complexity of judging whether a node is in a conflict area isO(M), in whichMis the number of nodes inG. The occupation relationship of the conflict areas among robots can form a directed graph, and the complexity of finding the circles in the directed graph isO(V+E) [10],VandEare the number of nodes and edges in the graph, respectively (Lines 17).Therefore, the complexity of the algorithm isO(HM(V+E)).
Experiments:Our experiments run on a desktop running Windows 10, equipped with an Intel(R) Xeon(R) Platinum 8280L 2.6 GHz and 64 GB of RAM.
To evaluate the performance of the proposed algorithm, this letter conducts experiments based on a real automated warehousing scenario. As shown in Fig. 2, automated forklifts perform transport tasks between work stations and storage points, the parameters of robots are shown in Table 1.
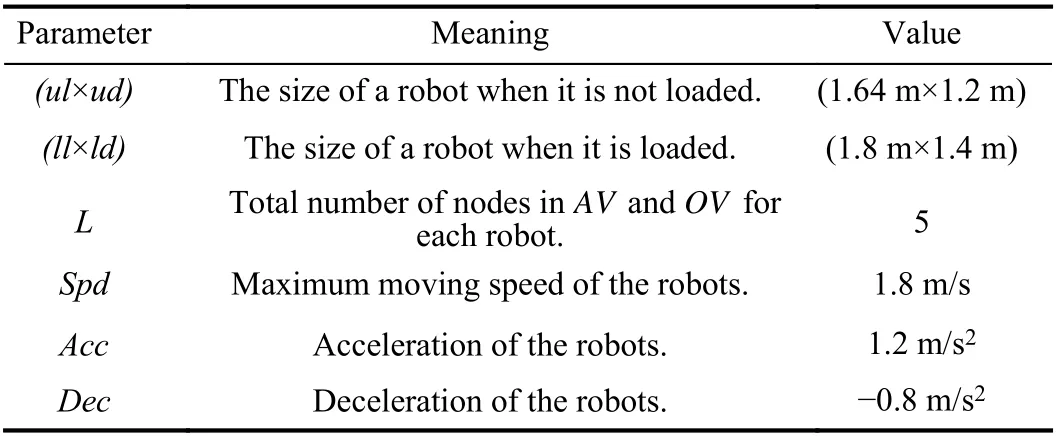
Table 1.Experimental Parameters of Robots
The proposed method based on glue nodes (GN) is compared with the following methods: Structural on-line control policy (SOCP) [3],spare zone based hierarchical motion coordination (SZH) [5] and method based on chains of reservations (COR) [4]. Each set of experiments was set up with 50 outbound tasks (the robots transport cargos from storage points to work stations) and 50 inbound tasks(the robots transport cargos from work stations to storage points).Tasks are always allocated to nearest idle robots. Each task consists of four subtasks: 1) move to a work station (or a storage point);2) load cargos; 3) move to a storage point (or a work station) with cargos; 4) unload cargos.
Three different indicators are used to evaluate the performance:average task execution time, average waiting time of the robots and the total mileages when robots execute tasks. The experimental results are shown in Table 2.
In terms of average task execution time, GN performs much better than other methods. When the number of robots is 8, GN consume 41.01%, 34.09% and 28.06% less time than COR, SOCP and SZH,respectively. This is because other methods cause more waiting time for the robots to avoid collisions and deadlocks than GN. Since the number of tasks remains the same in each experiment, the average task execution time reflects that GN is more efficient than other methods. In terms of total mileage, when using GN, the robot traveled less mileage (less energy consumption) than using other methods.
Both the average task execution time and the average waiting time increase with the number of robots, because more robots mean more congested traffic, and robots are more likely to wait to avoid collisions and deadlocks.
Conclusion:This letter proposes the concept of glued nodes in roadmaps. Based on glued nodes, a collision and deadlock avoidance method in multi-robot systems is proposed. The method can be applied to any roadmap without dividing the environment like the methods based on zone control. Experimental results show that the proposed method is more effective than several other methods.Anymore, the method proposed in this letter has been applied to many industrial projects, like manufacturing, warehousing and container terminal. For a detailed explanation of some concepts in this letter, please see the appendix. In the future, we will study the efficient method of calculating glued nodes and apply the method tolarge-scale scenarios.

Table 2.Simulation Results
 IEEE/CAA Journal of Automatica Sinica2022年7期
IEEE/CAA Journal of Automatica Sinica2022年7期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Driving as well as on a Sunny Day? Predicting Driver’s Fixation in Rainy Weather Conditions via a Dual-Branch Visual Model
- Structured Controller Design for Interconnected Systems via Nonlinear Programming
- Safety-Critical Model-Free Control for Multi-Target Tracking of USVs with Collision Avoidance
- A Novel Dynamic Watermarking-Based EKF Detection Method for FDIAs in Smart Grid
- Differentiable Automatic Data Augmentation by Proximal Update for Medical Image Segmentation
- Modeling and Analysis of Matthew Effect Under Switching Social Networks via Distributed Competition
