Safety-Critical Model-Free Control for Multi-Target Tracking of USVs with Collision Avoidance

Shengnan Gao,,, Zhouhua Peng,,, Haoliang Wang, Lu Liu,,, and Dan Wang,,

Dear editor,

This letter addresses the multi-target tracking of underactuated unmanned surface vehicles (USVs) subject to multiple stationary/moving obstacles. The kinetic model parameters of each USV are totally unknown. A safety-critical model-free control method is proposed for tracking multiple targets with a collision-free containment formation.Specifically, a distributed containment extended state observer(DCESO) is designed to estimate the convex hull spanned by the multiple targets. At the kinematic level, a collision-free kinematic guidance law is presented using a control barrier function (CBF) and an extended state observer for each follower USV. At the kinetic level, a model-free position tracking control law by using an adaptive ESO (AESO) is presented for each follower USV. By the designed safety-critical model-free control method, cooperative tracking of multiple targets under multiple stationary/moving obstacles can be achieved using completely unknown kinetic model parameters.Simulations are provided to illustrate the efficacy of the proposed safety-critical model-free control method for a fleet of USVs.

Related work:As an important tool for developing and protecting the ocean, marine vehicles are widely used in military and civil fields such as situation awareness of offshore areas, environmental monitoring, and cooperative rescue [1]−[6]. For diversified oceanic missions, different motion scenarios have been studied in recent years [7], including cooperative trajectory tracking, cooperative path following [1], cooperative target enclosing [8], and cooperative target tracking [9]. More specifically, cooperative target tracking is to force a swarm of follower marine vehicles to track one/multiple target vehicles.

Recently, target tracking of marine surface vehicles has aroused word-wide interest [9]−[12]. In [10] and [11], one follower vehicle can track one target vehicle subject to the unavailable target velocity.In [9], [12], a fleet of follower vehicles can track one target vehicle under the unavailable target velocity. However, the target tracking control methods in [9]−[12] can only achieve that one follower vehicle/multiple follower vehicles track one target. This will limit the autonomy level of USVs [13]. Besides, the target tracking control methods in [9]−[11] can not guarantee the collision free tracking.This may cause a failure of cooperative control [14]. Addition, the target tracking control methods in [9]−[12] assume that the kinetic vehicle model is a prior model. Nevertheless, the prior model is obtained from a large number of experiments. Besides, the prior model may suffer from variations in practical applications due to load change, actuator faults, or additive nonlinear disturbances induced by environmental circumstances [15]. More practically, it is highly desirable to design a model-free control method for USVs without a prior kinetic model.

In this letter, we aim to address the multi-target tracking of USVs subject to multiple stationary/moving obstacles, in addition to completely unknown kinetic model parameters. By using a DCESO to estimate the convex hull spanned by the multiple targets. A collision-free kinematic guidance law is designed for each follower USV using a CBF and an ESO at the kinematic level. Besides, the developed kinematic guidance law only uses the relative range and angle, which can be obtained by local sensors. At the kinetic level, a model-free position tracking control law using an AESO is designed for each follower USV. The contribution of the proposed control method is threefold. Firstly, the autonomy level of USVs is enhanced by achieving multiple follower USVs to track multi-target. Secondly,the CBFs are embedded into the guidance laws such that the USVs will not collide with stationary/moving obstacles and other USVs.Finally, the cooperative target tracking can be obtained without a prior kinetic model.

Problem statement:Consider a coordinated control system consisting ofNfollower USVs andMleader vehicles. The dynamic equation of theith follower USV can be described as

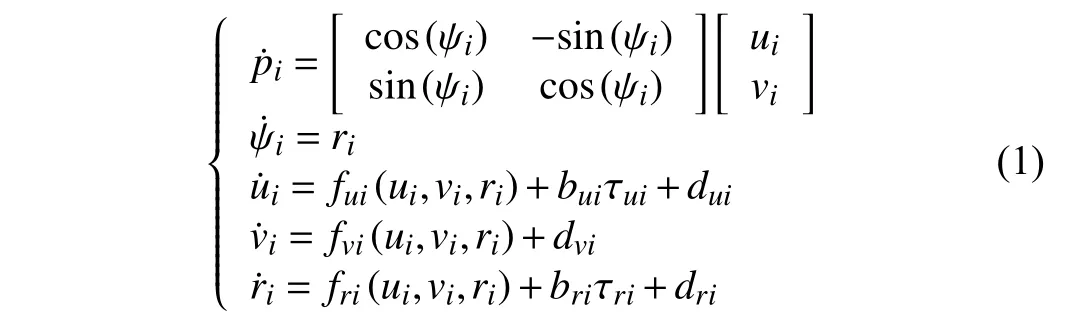
wherei= 1,…,N;pi=[xi,yi]Tand ψiare the position and heading angle of theith follower as shown in Fig. 1;ui,vi, andrirepresent the surge velocity, sway velocity and angular rate of theith follower;fui,fvi, andfrirepresent the uncertain nonlinearities including unmodeled hydrodynamics, hydrodynamic damping forces, and Coriolis forces;buiandbridenote the mass parameter; τuiand τuidenote the control input;dui,dvi, anddridenote the disturbance caused by wind, waves and ocean currents.

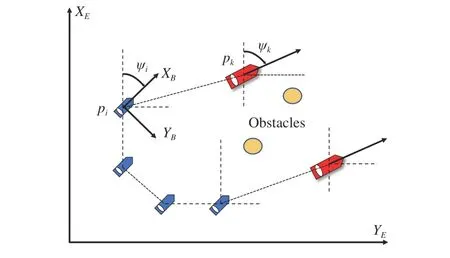
Fig. 1. The geometrical illustration of safety-critical model-free control.

TheNUSVs are supposed to trackMtarget vehicles and their positions are denoted bypk=[xk,yk]Twithk=N+1,N+2, …,N+M.

Assumption 1: For each follower USV, there is at least one target that can access to the follower USV.

The control objective of this letter is to design a safety-critical model-free control law for a fleet of follower USVs with dynamics(1) to track multiple target vehicles under multiple stationary/moving obstacles.

Basic concept:Consider a system asx˙=f(x)+g(x)u, wherex∈RNis the state,u∈RMis the input,f(x):RN→RN, andg(x):RN→RN×M. Let S ⊂F ⊂RNas the superlevel set ofh(x):RN→R,S={x∈RN|h(x)≥0}, ∂S={x∈RN|h(x)=0} andInt(S)={x∈RN|h(x)>0} . Ifhis a CBF, and the inequalityh˙(x)+κh(x)≥0,∀x∈F holds whereh˙(x)=∇h(f(x)+g(x)u) and κ ∈R+.

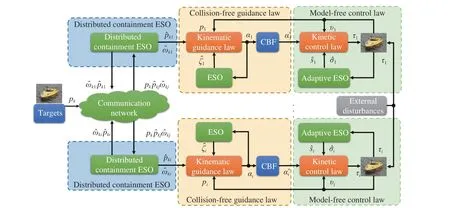
Fig. 2. The safety-critical model-free control architecture.

Design and analysis:Model-free control architecture for tracking multiple targets is shown in Fig. 2.

Distributed containment ESO: In this letter, the cooperative target tracking problem is addressed by a design of DCESO for followers to infer the convex hull spanned by the targets. The DCESO is designed as

Main results:

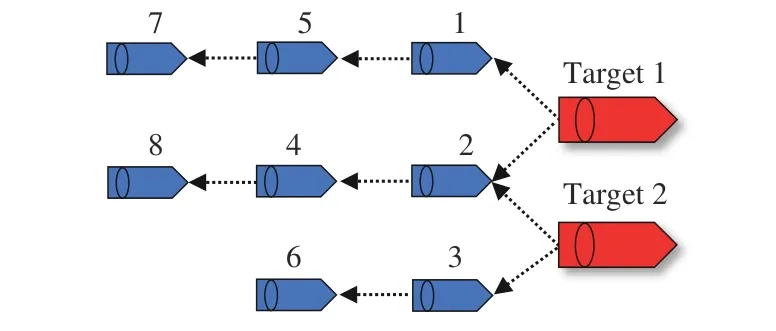
Fig. 3. Communication topology.

Simulation results are given in Figs. 4−6. Fig. 4 shows that the eight follower USVs can track two targets under two stationary obstacles. Fig.5 shows that the estimation performance of the DCESO. Fig. 6 shows the tracking errors.

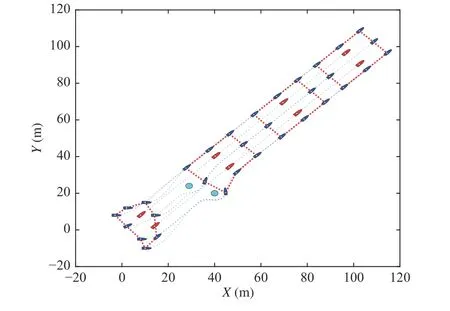
Fig. 4. Safety-critical model-free control performance.

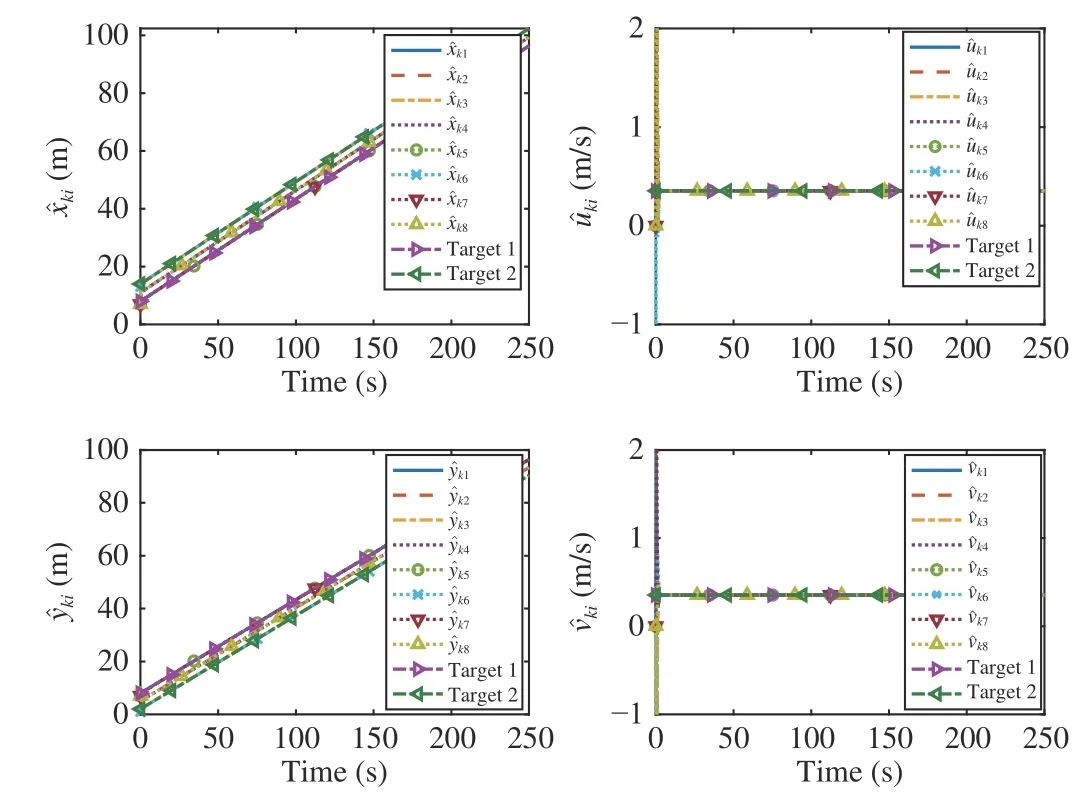
Fig. 5. Estimation performance of the DCESO.

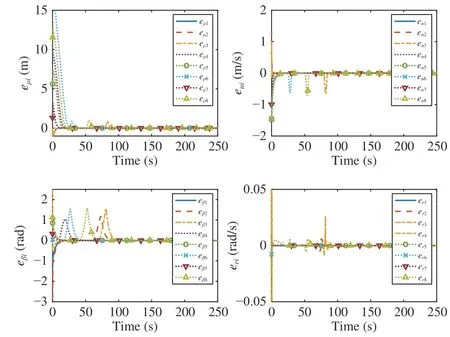
Fig. 6. Tracking errors.

Conclusions:This letter addresses the problem of multiple targets tracking of USVs in the presence of multiple stationary/moving obstacles, in addition to completely unknown kinetics. A DCESO is designed to estimate the convex hull formed by the multi-target. At the kinematic level, a collision-free kinematic guidance law is designed for each follower USV based on a CBF and an ESO. At the kinetic level, a model-free position tracking control law based on an AESO is proposed for each follower USV. Simulations are provided to illustrate the efficacy of the proposed safety-critical model-free control method for USVs.

Acknowledgments:This work was supported in part by the National Natural Science Foundation of China (51979020,51909021, 51939001, 52071044 ), the Top-notch Young Talents Program of China (36261402), the Liaoning Revitalization Talents Program (XLYC2007188), the Science and Technology Fund for Distinguished Young Scholars of Dalian (2018RJ08), the Basic Scientific Research in Colleges and Universities of Liaoning Provincial Education Department (LJKQZ2021007), and the Fundamental Research Funds for the Central Universities.