Ti掺杂扶手椅型石墨烯纳米带电子和光学性质的第一性原理研究

张 敏， 马 玲*， 张建民

(1.宁夏大学 物理与电子电气工程学院,宁夏 银川 750021； 2.陕西师范大学 物理学与信息技术学院,陕西 西安 710062)

石墨烯，一种由碳原子构成的六角蜂巢状的二维晶体，因具有超高的电子迁移率、巨大的比表面积、极高的透光性和弹道特性[1—4]，可广泛应用于电子器件、光电器件[5—6]、储能[7—8]、气体[9—10]和生物传感[11—13]等领域.石墨烯优异的电子性能源于其独特的电子结构，即：在石墨烯的能带结构中，最低未占据导带(LUCB)和最高占据价带(HOVB)相切于高对称点处，带隙为零且色散关系呈线性.然而，零带隙特征却限制了石墨烯在某些电子器件中的应用.因此，设法打开石墨烯带隙以扩大其应用范围是非常必要的.解决方法之一就是把石墨烯剪裁成一维的纳米带.研究发现横向的量子限域效应可以在石墨烯纳米带中产生带隙[14].

石墨烯纳米带(GNRs)，是将石墨烯沿一定方向蚀刻或机械切割而成[15].蚀刻或机械切割的方向不同，纳米带的边缘形状则不同.分别沿着石墨烯中正六边形的一条边或垂直于该边的方向切割，可获得两种不同形状边缘的纳米带：扶手椅型纳米带(AGNRs)和锯齿型(ZGNRs)纳米带，其边缘形状及带宽的变化会影响石墨烯纳米带的电子性质.任意宽度的AGNRs均表现为半导体性，并且AGNRs的带隙(ΔN)随着带宽(N)的增加呈现周期性的振荡，带宽N分为3类，N= 3n，3n+ 1，3n+ 2，对应的带隙：Δ3n+1>Δ3n>Δ3n+2(n为自然数)[16].基态的ZGNRs具有反铁磁性 (AFM)和半导体性.能带结构中，靠近费米能级的LUCB 和HOVB色散小，且几乎平行于费米能级，并主要源于ZGNRs边缘碳原子上电荷的贡献，因此被称为边缘态[17—19].

杂质原子的取代性掺杂能够有效地调控石墨烯纳米带的电子结构和光学性质，以满足某些应用的要求[20—28].一般地， N和B原子可作为碳基纳米材料的首选掺杂剂，因为它们的原子半径与C原子相近，替换掺杂后几乎不会导致石墨烯变形，能保持其结构的稳定性.Cruze-Silva等[21]采用密度泛函理论研究了单个N和B原子取代性掺杂AGNRs和ZGNRs的形成能、电子结构及磁学性质.研究发现：除B掺杂AGNRs情况外，AGNRs和ZGNRs边缘上的C原子更容易被N或B原子取代，依据形成能的计算结果，AGNRs边缘碳原子的邻位更容易被B原子取代；当B替代掺杂ZGNRs边缘上的C原子时，展现出施主特征；B的掺杂位处于纳米带中心时，体系表现出受主特征，而N替代掺杂的ZGNRs与之相反[21].N或B原子掺杂的AGNRs依然没有磁性，而两种原子的掺杂使得反铁磁性的ZGNRs转变为铁磁性，并且伴随着掺杂原子从边缘移到中心，掺杂体系的磁矩逐渐减小；Huang等[22]研究发现当ZGNRs的边缘出现空位或B原子的替代性掺杂时，空位和B原子处的自旋被完全抑制，距其较远区域的自旋分布受到的影响较小.另外，过渡金属原子也可作为掺杂剂，用以诱发体系产生磁性或调控体系的磁矩及自旋分布[23—28].例如，Hu等[23]研究了Au嵌入ZGNRs不同位置时的电子性质和磁性特征，结果表明：掺杂体系的基态是反铁磁性还是铁磁性取决于Au的掺杂位置；无论Au的掺杂位置如何，Au嵌入ZGNRs始终表现为自旋零带隙特征(Spin gapless semiconductor)；Lee 等[24]研究分析了Co掺杂ZGNRs的稳定性和磁相互作用，结果表明，两个Co原子掺杂时，其间的磁相互作用依赖于Co原子的掺杂位置.与此同时，取代性掺杂也会影响石墨烯纳米带的光学性质.例如：与纯净的GNRs相比，B掺杂AGNRs的吸收系数在2.0～3.3 eV的频率范围内增加[29].

目前，有关Ti掺杂AGNRs的电子结构和光学性质的研究报道很少.因此，本文采用第一性原理计算方法系统地研究了Ti原子在不同位置、以不同浓度进行取代性掺杂对AGNR(7,4)电子结构和光学性质的影响.该项研究有利于推动石墨烯纳米带在纳米电子和光电器件方面的应用.

1 计算方法

本文采用基于密度泛函理论第一性原理计算方法的VASP软件包[30]进行计算.电子和离子之间的相互作用通过投影缀加波(PAW)方法[31]进行描述，电子间的交换和关联性通过Perdew-Burke-Ernzerhof (PBE)函数[32]下的广义梯度近似(GGA)进行处理.经测试，获得的平面波基组的截断动能值为400 eV.采用共轭梯度算法对结构进行离子驰豫，直到作用在每个原子上的力小于0.2 eV/nm，且在电子自洽迭代过程中能量收敛小于10-4eV时优化停止.选取11×1×1的K点抽样网格点计算布里渊区积分，采用以Gamma点为中心的Monkhorst-Pack方法[33]产生K点，高斯拖尾展宽为0.2 eV.采用具有周期性边界条件的超胞，在相邻纳米带之间添加1.5 nm的真空层消除它们之间的相互作用.所有掺杂体系光学性质的研究均借助如下频率相关的复介电函数来计算：

ε(ω)=ε1(ω)+iε2(ω).

(1)

在长波极限下，虚部ε2表示如下：

ε2(q→0,ε)=

(2)

复介电函数中的实部与虚部有关，可用Kramers-Kronig变换[34—35]从虚部ε2计算得出，即

ε1(ε)=

(3)

式中：P为Cauchy值，文献[36]对该技术进行了很好的解释.

吸收系数α(ω)由下式给出：

(4)

式中：c为真空中的光速；ω为能量单位.

2 结果和讨论

2.1 AGNR(7,4)的优化结构和电子性质

选取AGNR(7, 4)作为掺杂的原始构型并进行优化(图1a).其中两条黑色虚线之间的部分为AGNR的原胞.根据扶手椅型石墨烯纳米带的定义方法，“7” 表示横过石墨烯纳米带二聚物的条数，即代表纳米带的宽度，“4”表示AGNR(7, 4)是由4个宽度为“7”的AGNR原胞构成.超晶胞AGNR(7, 4)包含16个H原子和56个C原子.为了防止石墨烯纳米带结构优化之后发生重构，采用氢原子将边缘碳原子上的悬挂键进行饱和.A,B,C,D代表4个取代位，绿色和粉色的球分别代表C原子和H原子.优化后，钝化边缘的氢原子与碳原子在同一平面内，说明C—H键和C—C键一样，也是以sp2杂化方式耦合.经测量，石墨烯纳米带边缘处的C—H键和C—C键键长分别为0.109 nm和0.142 nm.图1b给出了AGNR(7, 4)的能带结构和带分解电荷密度图，其中电荷等密度面值为2 e/nm3.显然AGNR(7,4)是具有直接带隙的半导体且带隙为1.68 eV.费米能级附近的LUCB和HOVB色散较小，且主要源于靠近AGNR(7, 4)边缘处的C原子以及纳米带中央处的C原子上电荷的贡献，这与ZGNRs不同.

图1 AGNR(7, 4)的优化结构及其能带结构和带分解电荷密度

2.2 Tix@AGNR(7,4)的优化结构和电子性质

在AGNR(7, 4)中，从边缘到中心选取4种可能的取代位，分别标记为A,B,C,D (图1 a)，相应的掺杂构型依次记作Ti-A-AGNR(7, 4)，Ti-B-AGNR(7, 4)，Ti-C-AGNR(7, 4)，Ti-D-AGNR(7, 4)，其中蓝色球、绿色球、粉色球分别代表Ti原子、C原子和H原子.为了寻求最稳定的掺杂构型，计算上述4种掺杂构型的形成能Ef[37]，定义如下：

式中：Ed为Ti原子掺杂AGNR(7, 4)的总能量；i为掺杂原子的种类，这里表示Ti原子；ni为“i”型原子的个数；μi为“i”型原子的化学势.表1为相应的形成能的计算结果.由表1可知，Ti-A-AGNR(7, 4)的形成能最低，即AGNR(7, 4)边缘上C原子最容易被Ti原子取代.

表1 单个Ti原子在4个不同位置掺杂下的AGNR(7, 4)的形成能 eV

图2为Ti原子在4种不同位置掺杂的AGNR(7,4)的优化结构.由图2可见，掺杂Ti原子后，C—Ti键长0.188～0.202 nm，大于C—C键长0.142 nm，这是因为Ti原子的离子半径(0.061 nm)远比C原子的离子半径(0.016 nm)大.Ti原子突出纳米带所在平面，石墨烯纳米带的六角形环发生了明显的变形.由于Ti原子和H原子之间是以sd2杂化方式进行键合，因此Ti—H键沿展的方向明显与C—H键不同.图3给出了Ti原子在不同位置掺杂的AGNR(7, 4)的能带结构和带分解电荷密度图，蓝色球代表Ti原子且电荷等密度面值为2 e/nm3.与纯净的AGNR(7, 4)相比，Ti原子在不同位置掺杂，掺杂体系的带隙减小.费米能级附近的LUCB 和HOVB色散仍然较小，主要来源于Ti1@AGNR(7, 4) 中Ti原子及其周围C原子的电荷贡献，因此LUCB 和HOVB为杂质诱导带.

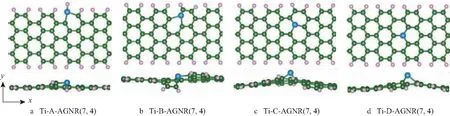
图2 Ti掺杂AGNR(7, 4)在4种不同掺杂位置的优化结构

图3 单个Ti原子在4种不同位置掺杂的AGNR(7, 4)的能带结构和带分解电荷密度

根据上文研究结果，Ti原子在AGNR(7, 4)边缘处掺杂时更为稳定，因此，选取纳米带边缘处的C原子为取代位，如图4所示，掺杂位分别用S1～S4表示.为方便表述，掺杂构型记作Tix@AGNR(7, 4)，其中x=1～4，表示AGNR(7, 4)中掺杂Ti原子的数目，相应的掺杂浓度依次为1.39%,2.78%,4.17%,5.56%.

图4 在AGNR(7, 4)的结构中4个不同掺杂位置S1～S4

图5给出了不同掺杂浓度下Ti掺杂AGNR(7,4)的优化构型.为了分析原子之间成键，绘制了4种构型的电子局域密度分布图(ELF).如图6所示,C—C以及C—H之间所成键均为共价键，并且H原子周围和C—H原子之间的ELF值明显大于C原子周围和C—C原子之间的ELF值.这是H原子的电负性比C原子的大，H原子吸引电子能力更强的缘故.Ti是金属元素，容易失去电子，因此Ti—H键具有离子键特征，H获得电子，故Ti—H之间电子集中分布在H原子周围；Ti—C键也是离子键，且电子局域分布在C原子周围.显然，掺杂浓度为4.17%和5.56%，纳米带边缘同侧相邻的Ti原子之间没有键合(见图6c和图6d)，这表明掺杂体系不会发生Ti原子的团簇现象.

图5 Tix@AGNR(7, 4)的优化结构

图6 Tix@AGNR(7, 4) (1 0 0)面的ELF

图7描绘了Tix@AGNR(7, 4)的能带结构和带分解的电荷密度图，蓝色球代表Ti原子且电荷等密度面值为2 e/nm3.由图7可以观察到，随着Ti掺杂浓度的增加，掺杂体系的带隙逐渐减小，LUCB和HOVB的色散逐渐增大.这说明，无论掺杂浓度如何，杂质诱导带LUCB和HOVB主要是源于Ti原子和近邻的C原子上的电荷贡献，且掺杂的浓度越大，电荷分布更加局域在Ti原子上.Ti的掺杂不会改变AGNR (7, 4)半导体性，其原因为Ti原子的最外层价电子结构为3d24s2，与C原子最外层的价电子的数目相同.

图7 Tix@AGNR(7, 4)的能带结构和带分解电荷密度

2.3 Tix@AGNR(7,4)的光学性质

2.3.1介电函数的虚部 在AGNR(7, 4)中引入Ti原子，不仅可以改变体系的电子结构，还能使光学性质发生变化.图8给出了在长波极限下，纯净石墨烯(PG)和AGNR(7, 4)在平行(E∥)和垂直(E⊥)极化时的介电函数虚部随频率变化的曲线.由图8a可见，在E∥极化下，两个特征峰分别位于4.03 eV和13.97 eV(分别用X和Y指示)；而在E⊥极化下，两个特征峰分别位于11.13 eV和14.45 eV(分别用A和B指示)，这与O. Olaniyan等[37]计算的结果非常吻合.对于E∥极化下的AGNR(7,4)，低频区的特征峰位于1.71 eV和3.59 eV(分别用X和Y指示)；高频区的特征峰出现在12.34 eV(用Z指示),其中，1.71 eV处的特征峰的产生源于Γ点处LUCB和HOVB之间电子的跃迁(图1b).对于E⊥极化，在10.94 eV和14.19 eV处出现两个特征峰(分别用A和B指示)(图8b).与PG相比，两种极化下，高频区的特征峰的强度显著降低.

图8 纯净石墨烯和AGNR(7,4)的介电函数虚部的频率变化曲线

Ti原子的掺杂及掺杂浓度的改变对介电函数虚部的影响可通过图9分析.图9描绘了在E∥和E⊥极化下的Tix@AGNR(7,4)介电函数虚部ε2随频率变化的曲线.在E∥极化下(图9a)，相对于1.71 eV处AGNR(7,4)的特征峰，该处Tix@AGNR(7,4)的特征峰的强度随掺杂浓度的增加而降低，且均发生微小的红移.在6～8 eV的频率范围内，Tix@AGNR(7,4)虚部ε2的值明显增加，且随着掺杂浓度的增加而增加.在E⊥极化下(图9b)，Tix@AGNR(7,4)的特征峰相较于AGNR(7,4) 在10.94 eV和14.19 eV处的特征峰，强度随掺杂浓度的增大而降低，且发生微小红移.在3～9 eV的紫外区，AGNR(7,4)虚部ε2的值近乎为零，随着掺杂浓度的增加，其值逐渐增大并出现新的峰.新峰的出现是因为引入Ti原子后，在费米能级附近出现了杂质态，这些态与其他态之间可能发生新的电子跃迁所致.

图9 E∥和E⊥极化下Tix@AGNR(7,4)在不同掺杂浓度下介电函数虚部的频率变化曲线

2.3.2吸收谱E∥和E⊥极化下Tix@AGNR(7,4)的吸收谱见图10.在E∥极化下，在低频区的1.97 eV处，相对于AGNR(7,4)，Tix@AGNR(7,4)在该处的吸收峰的强度随掺杂浓度的增加而降低，并发生微小的红移；而高频区在14.36 eV处，Tix@AGNR(7,4) 吸收峰的强度同样是随掺杂浓度的增加而降低，其中仅Ti1@AGNR(7,4)吸收峰的强度高于AGNR(7,4)；在6～8 eV的频率范围内，Ti原子的引入使得掺杂体系在该区间范围出现新的吸收峰，其强度随掺杂浓度的增加而增加.对于E⊥极化，在3～9 eV的紫外区，Ti掺杂会导致吸收系数增加，且随掺杂浓度的增加而增加.因此，对于AGNR(7,4)，可以通过改变Ti的掺杂浓度来有效调控特定频率范围内的吸收系数αmax.

图10 E∥和E⊥极化下Tix@AGNR(7,4)的吸收谱

3 结论

通过基于密度泛函理论的第一性原理计算，本文系统地研究了Ti在不同位置和不同浓度掺杂下AGNR(7,4)的电子结构和光学性质.主要结果如下：

1)改变Ti原子的掺杂位置和掺杂浓度，AGNR(7,4)仍保持原有的半导体性；

2)掺杂体系的带隙随Ti掺杂浓度的增加而逐渐减小；

3)在AGNR(7,4)中引入Ti原子后，费米能级附近的LUCB和HOVB由靠近边缘处的C原子和纳米带中央处的C原子上的电荷贡献转变为由Ti原子和近邻的C原子上的电荷贡献，且掺杂浓度越大，电荷分布越局域在Ti原子上；

4)对于E∥极化下的掺杂体系，在6～8 eV频率范围内虚部ε2和吸收系数αmax的强度均随掺杂浓度的增加而增加；

5)在E⊥极化作用下，在3～9 eV的紫外线范围内虚部和吸收谱均出现新的峰，其峰值均随掺杂浓度的增加而增强，这表明：Tix@AGNR(7,4)能吸收特定波长的紫外光，且吸收强度由掺杂浓度决定.

这些结果对石墨烯纳米带在纳米电子和光电器件的设计和应用有一定的理论指导作用.