湖南省多尺度降水序列混沌特性空间分异

杨家亮，崔 璨，李淑雅，欧阳也能，龙秋波，李大勇

(1.湖南省水利水电勘测设计规划研究总院有限公司，湖南 长沙 410007；2.河海大学水文水资源学院，江苏 南京 210098;3.湖南省水文地质环境地质调查监测所，湖南 长沙 410129；4.长沙理工大学水利与环境工程学院，湖南 长沙 410004；5.湖南省气候中心，湖南 长沙 4100043)

1 概述

降水系统是一个复杂的非线性系统，在气候、地形及人类活动等多重因素影响下表现出并非随机却貌似随机的特性[1]，具有产生混沌的基本条件。混沌学理论自20世纪80年代开始就被应用于水文学中，主要涵盖了水文时间序列的相空间重构[2]、混沌特性识别[3]、混沌预测[4]以及混沌优化算法[5]等方面的研究。由于降水过程的内在系统动力结构[6]较为复杂，采用传统的确定性方法或随机统计理论来挖掘降水规律存在一定的局限性，因此众多学者开展了对降雨序列混沌识别的研究。常用的混沌识别方法包括庞加莱截面法、关联维数法、最大Lyapunov指数法、Kolmogorov熵法等，但这些方法多数需要基于相空间重构来实现，目前尚缺少客观的指标对相空间重构的效果进行度量；同时，上述方法无法很好地区分混沌序列与随机序列[7]。相比较下，0-1混沌判别法[8-9]不依赖相空间重构，而是通过Chebyshev映射直接作用于时间序列的优点[10]，使其迅速成为众多学者研究的热点。

湖南省作为中国水资源时空分布不均的代表省份，受亚热带季风气候影响显著，降水时空分布不均，年际变化大，降水系统的混沌特性较为明显。以往针对该地区的研究多探讨的是降水序列本身的非线性特征和混沌现象，但并没有形成对不同时间尺度降水序列变化规律差异性的共同认识，且多是利用传统的随机统计理论对降水时空分布[11-12]、动态趋势[13]和降水分区[14]等进行分析，尚缺乏全省降水混沌特性的空间分布研究。因此，本文引入0-1混沌测试方法对湖南省97个雨量站(建站—2017年)不同尺度(候、旬、月)的降水序列进行混沌识别，以分析不同时间尺度下降水混沌特性的空间分布特征，并探讨其影响因素。

2 研究区与数据来源

湖南省坐落于东部沿海和中西部地区过渡带，地貌类型复杂多样，东、南、西三面山地围绕，中部多岗地丘陵，北部平原河网发育，整体呈北向开口的马蹄状地形。属大陆性亚热带季风湿润气候，四季分明，冬冷夏热，春温多变，夏秋多旱，雨水集中，多年平均降雨量1450mm。

大气环流是影响湖南省降水混沌特性的重要因素之一。在西风环流中，青藏高原位于上风方，产生了独特的高原季风，使得大气环流产生分支、绕流与汇合现象，其热力、动力影响加强了季风气候；同时，横亘湘南部边界的南岭山脉，阻挡冷空气南下，对持续低温和阴雨产生直接影响；此外，湖南省的地形分布使其雨、热等气候要素等值线打破了与纬线平行的一般规律，年均降水空间分布不均，湘东部降水量丰富，呈“人”字形分布，始于雪峰山脉北端，向湘东、湘南地区延伸，年均降水量约为1400～1600mm，而洞庭湖区、湘西地区、邵阳岩溶盆地仅为1240～1360mm，是湖南省3大降雨低值区。

本文主要研究湖南省不同时间尺度下降水混沌特性的空间分异特征，所利用的97个雨量站自建站至2017年的日雨量数据来自湖南省气象局。

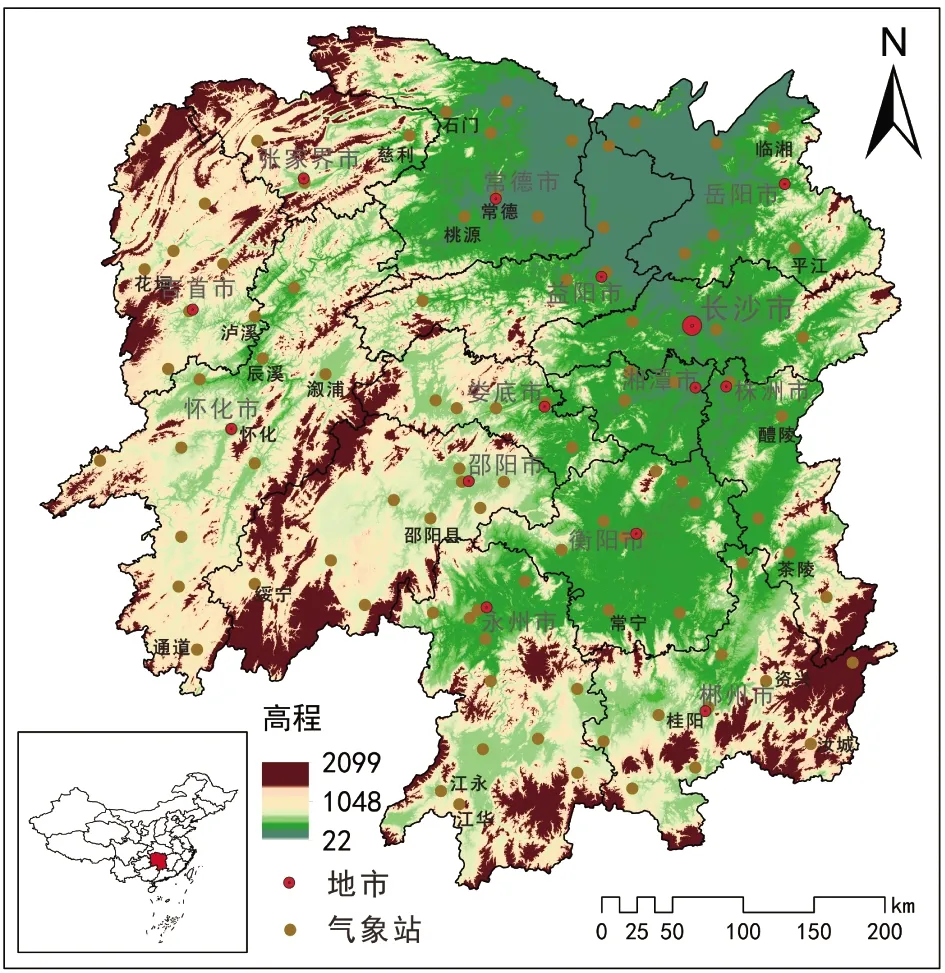
图1 湖南省地形及雨量站分布图

3 研究方法

本文采用0-1混沌测试方法对降水序列的混沌特性进行识别和检验。该方法最早由Gottwald和Melbourne提出[8-9]，其优点为不需要对离散时间序列进行相空间重构，只需根据渐进增长率的输出结果是否趋近于1或0，即可直接判断序列具有混沌特性与否，相较于最大Lyapunov指数法、饱和关联维数法等更加简便、快速。该方法的原理和步骤如下：

(1)转化函数

首先，定义转化函数pc(n)和qc(n)，二者的散布特征在一定程度上是对混沌特性的表达。若时间序列存在周期性，则p(n)-q(n)轨迹相图有界稳定；否则表现为布朗运动。

(1)

(2)

式中，φ(j)—离散时间序列，其中j=1，2…，N;c—一随机常数，c∈[0，π]。

(2)均方位移

基于转化函数pc(n)和qc(n)，定义均方位移Mc(n)为：

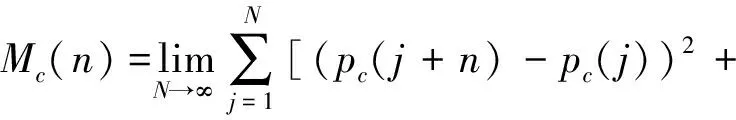
(qc(j+n)-qc(j))2]

(3)

通常根据均方位移Mc(n)的敛散性来判断时间序列的混沌性，但研究表明Mc(n)的收敛效果不好[15]，因此给出修正均方位移M(n)的计算公式：

M(n)=Mc(n)-(E(φ))2

((1-cosnc)/(1-cosc))

(4)

(5)

式中，n需满足≪N，在实际应用中建议nc=N/10时效果更好。

相比起Mc(n)，经过修正之后的M(n)保留了原始函数的渐进增长特性，同时其收敛性得到了加强。此时时间序列具有混沌性是M(n)随时间线性增长的充分不必要条件，若时间序列非混沌，则M(n)为一有界函数。鉴于降水序列为非连续的有限序列，因此用均值E(φ)*替代E(φ)，计算公式为：

(6)

式中，xi—候、旬、月降水序列。

(3)渐进增长率

采用M(n)对应于n的渐进增长率Kc来定量描述M(n)的增长特性，进而判断出序列是否具有显著的混沌特征。计算时需要选取Nc个随机常数，得到Nc个Kc。由于伴随着共振Kc的中值相对于极端值表现为鲁棒性，因此通过计算Kc的中值来判断时间序列的混沌特性。通常将线性回归法或关联系数法用于估计渐进增长率Kc。

①线性回归法。把Kc定义为lgM(n)与lgn的线性回归系数：

(7)

②关联系数法。定义向量ξ=(1，2，3…n)和向量M=(M(1)，M(2)，…，M(n))，则关联系数Kc可以通过下式得到：

(8)

(9)

式中，x、y为给定降水序列；q为x、y的序列长度；cov(x，y)为协方差；var(·)为方差。

本文采用关联系数法计算渐进增长率。若Kc趋近于1，则该时间序列高度混沌；反之，若Kc趋近于0，则该时间序列呈现周期性、倍比性等规律。

4 结果与分析

4.1 降水0- 1混沌识别

令随机数c的个数Nc等于8000，运用0-1混沌测试方法对全省候、旬和月3个时间尺度下不同雨量站降水序列均方位移对应的渐进增长率K进行计算，所得计算结果显示：渐进增长率均值随时间尺度的增长呈现出减弱趋势，候、旬、月时间尺度下K的最大值分别为0.9940、0.9934、0.9917；最小值分别0.9927、0.9919、0.9855。

在97个雨量站中，邵阳市绥宁县雨量站月尺度下的渐进增长率为0.9829，系所有雨量站多尺度0-1混沌测试计算所得K的最小值。因此选取绥宁站为代表雨量站，若该站能通过混沌检验，则证明其他雨量站月尺度甚至更短尺度下的降水序列也具备混沌性。图2(a)为绥宁县雨量站月降水序列转换函数p(n)-q(n)的轨迹相图，二者表现为连续的随机布朗运动；图2(b)为均方位移M(n)-t关系曲线，M(n)随时间t呈现出明显的线性增长特点；图2(c)为Kc-c变化散点图，由图可知，除特殊点外，渐进增长率基本趋近于1。综合以上几点，可以推断湖南省各雨量站的逐候、逐旬、逐月降水序列具有明显的混沌特性，同时也说明了0-1混沌测试的有效性。

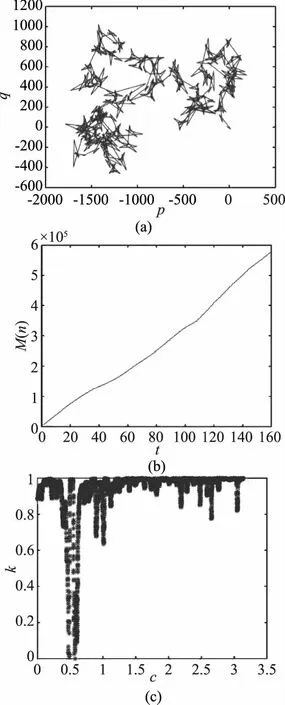
图2 基于0-1方法的绥宁站逐月降水序列混沌测试

4.2 不同时间尺度降水混沌特性空间分布

根据计算的不同时间尺度降水序列的渐进增长率K值，运用Kriging方法对各雨量站的K值进行空间插值，得到全省候、旬、月3个时间尺度降水序列的K值分布，如图3所示。从不同时间尺度渐进增长率的大小来看，在候、旬、月尺度下，湖南省多个雨量站K的最小值分别为0.9927、0.9919、0.9855，平均值分别为0.9935、0.9928、0.9895，最大值分别为0.9941、0.9934、0.9921，降水混沌特性总体上候>旬>月。

从降水混沌特性的空间分布来看，同一时间尺度下，降水序列的渐进增长率呈现出明显的空间分异特征；而不同时间尺度下，降水序列的渐进增长率均表现出明显的空间集聚特征。在候尺度上，渐进增长率K的主高值区主要分布在郴州至邵阳一带，次高值区位于湘北岳阳一带；渐进增长率K的主低值区主要分布在以怀化市辰溪县、湘西州泸溪县为中心的西部地区，次低值区则分布在湘东的长株潭一带，并与湘西主低值区连片形成低值槽。

旬尺度降水序列与月尺度降水序列的渐进增长率在空间分布上保持了较好的一致性，总体表现为由东北西南向伸展的“人”字形分布特征，即自湘北经湘东北至湘东南为K的高值分布区，而湘西、湘西南和湘中则为K的低值分布区。但旬、月尺度降水序列K的低值中心略有不同，旬尺度K的低值中心位于怀化市，呈均匀圆环形向外辐射，低值范围较大；月尺度K的低值中心则位于绥宁县，呈点状辐射，低值范围较小。

与候尺度降水序列相比，旬、月尺度降水序列K值的空间差异主要体现在3个区域，即湘北张家界-常德一带的相对高值区，湘东株洲-醴陵一带的相对高值区，及衡邵永盆地的相对低值区。

4.3 降水混沌动力系统分析

降水系统是一个复杂的非线性系统，既受地球整体大气循环总体规律的控制，又受局部地表形态、海陆位置等复杂因素的影响，具有对初始条件的敏感性和内在随机性[16]。一般来说，时间序列的非确定性因素越多，其非线性特性表现就越明显。小尺度降水序列隐含更多的局部地理信息，而大尺度降水序列主要反映区域大气环流的动力学特性。从图3可以看出，总体上候、旬、月尺度降水序列的K值分布具有相近的分布特征，且尺度越大越趋近于稳定。

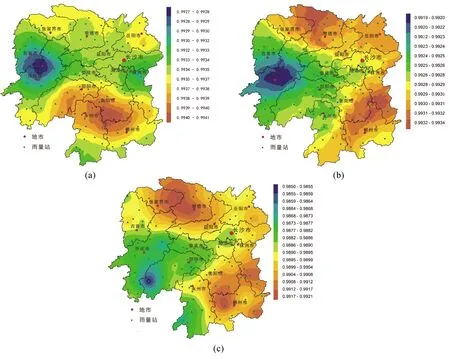
图3 湖南省不同尺度降雨系列K值分布.(a)、(b)、(c)分别为候尺度、旬尺度、月尺度

湖南省降水主要受东亚季风环流、印度季风环流和中纬度西风带等的影响[14]。在夏季风期间，湖南水汽主要来自孟加拉湾、南海洋面与西太平洋海区[17-18]，而在冬季风期间，水汽主要来自西风带携带的水汽和局地水汽环流[19]，水汽输送主要依靠西风环流和南下的大陆性气团[20]。已有研究运用0-1方法对中国降水开展了混沌识别及分区，结果表明，降水序列渐进增长率的平均值在中国西南地区最低，在中国东部的秦岭-淮河以南地区最高，其中起洞庭湖区自长江中下游平原一带为K的高值中心。这种空间分布格局主要来源于西太平洋副热带高压对天气系统的影响，且随着季节变化，副热带高压带的范围和强度会发生明显变化。根据近60年西太平洋副热带高压对中国夏季降水影响的统计结果[21]，西太平洋副热带高压脊线指数的平均值为24.15°N，北界指数为29.58°N，西伸脊点多年平均值约为119.25°E，覆盖范围西端可至鄂西到湘中一带。

湖南省旬、月尺度降水序列渐进增长率的空间分布与前人的研究成果基本保持了良好的一致性，反映了中国南方西太平洋副热带高压对降水动力系统产生的影响。湖南省东部受西太平副热带高压影响、东南部受台风雨影响均较大，因此降水序列K在湖南省东北部和东南部呈现高值；省西南部则受到印度季风环流和中纬度西风带影响，从而表现出与中国西南地区相近的低K值。而候尺度降水序列K值更多反映的是小尺度范围内的地理信息及局部动力学特征。如在衡阳盆地与邵阳盆地的连接带，即衡邵娄干旱走廊[22]，形成了以郴州至邵阳为边界的均匀的环形高K值区，这与其盆地地形及岩溶地质条件相对应，该区域东、中、西部的四方山、衡山、九峰山等高大山脉阻挡了湿润季风气流，使得其气候特征明显区别于其他地区，多年来干旱少雨，而能越过山脉进入盆地的多为强气流，导致短时间内盆地大量集中降雨形成内涝，因此该地区表现出较强的降雨混沌特性。

5 结论

(1)湖南省97个雨量站候、旬、月尺度降水序列均表现出较强混沌特性，且随着时间尺度增加，渐进增长率呈现减小趋势，即混沌特性呈减弱趋势。

(2)在同一时间尺度下，降水序列的混沌特性呈现出明显的空间分异特征；而在不同时间尺度下，降水序列的混沌特性均表现出明显的空间集聚和分区特征，且随尺度增加趋于稳定。旬、月尺度降水序列的渐进增长率在空间上表现为湘东北、湘东南高，湘中、湘西南低的特点；候尺度降水序列的渐进增长率明显区别于旬、月尺度，即湘北、湘东的部分地区表现为相对低值区，湘东南的衡邵永盆地表现为相对高值区。

(3)湖南省候、旬、月尺度降水序列混沌特性的空间分布主要受区域降水动力学特征控制，其中，旬、月尺度的渐进增长率更多地反映了大尺度的大气环流动力学特征，而候尺度则是对局部地理信息及降水动力学特征的体现。从影响要素来看，西太平洋副热带高压主要控制了旬、月尺度下湘东北、东南部的高值区，而候尺度下衡邵永干旱走廊高值区的形成则主要与其盆地地形有关。