汽轮发电机组甩负荷测试及仿真分析

杨彦平，贾 斌，李晓波

（内蒙古电力（集团）有限责任公司内蒙古电力科学研究院分公司，呼和浩特 010020）

0 引言

机组甩负荷试验的主要目的是检验调节系统动态特性是否符合设计及运行要求，并通过甩负荷试验数据计算动态超调量、转子时间常数及转子转动惯量等特征值[1-3]。其中转子转动惯量特征值对电力系统稳定器参数整定计算及采用测功法进行甩负荷试验中转子飞升转速计算都有重要意义[4]。

目前，国内外对汽轮发电机组转子转动惯量的计算研究较少：田丰[5]提出了使用时域2点邻近点平均或频域快速傅里叶变换滤波计算转子转动惯量，该方法需要人工读取调节汽阀延迟关闭时间；鲍文龙等[6]提出了基于卡尔曼自适应滤波器的转子转动惯量计算方法，但建模机理复杂，包括操作量度对结果影响较大。

本文以某电厂350 MW 机组甩负荷试验为例，就参数测量、数据处理、建模及仿真计算进行分析。转速测量环节转速测量误差叠加环境噪声并不能反映转速信号的真实值，本文对采集到的转速数据通过移动平均滤波，对滤波数据利用S 型函数及LM 优化算法进行最小二乘拟合，对拟合数据一阶微分求解，得到转子最大加速度，以期解决传统手工计算选取时间间隔求解最大加速度带来的计算误差，得到更准确的转子转动惯量值。

1 机组概况

某电厂350 MW机组汽轮机为哈尔滨汽轮机厂制造的超临界、一次中间再热、双缸双排汽、单轴凝汽式汽轮机，机组启动采用高中压缸联合启动方式。锅炉为哈尔滨锅炉厂制造的超临界参数变压运行直流炉。发电机为哈尔滨电机厂有限责任公司制造的三相交流隐极式同步发电机。机组控制系统采用上海新华控制技术有限公司生产的XDC-800集散控制系统。

2 参数测量

2.1 转子转动惯量计算原理

大型汽轮发电机转子由高中压转子、低压转子及发电机转子通过联轴器连接，其几何形状复杂，质量分布也不均匀，制造厂难以给出转子转动惯量准确值，因此主要通过常规法甩负荷试验方法[7]进行测取。利用汽轮机在甩负荷较短时间内调节汽阀尚未关闭，进入转子的蒸汽流量尚未发生变化，机械功率即为甩负荷试验前功率。测取有关数据，计算转子转动惯量：

2.2 数据采集

甩负荷试验数据采集选用16 通道DL850 型快速录波仪，数据采集过程中串联50 Ω电阻，将模拟量输出的4～20 mA电流信号转化为电压信号。功率信号选取由功率变送器输出的模拟量输入（Analog Input，AI）信号，转速信号选取汽轮机安全监视系统（Turbine Supervisory Instrumentation，TSI）零转速信号。零转速信号不带保护，且测量精度高，测速时测速传感器通过测量探头与测速齿盘轮间的高、低电压变化形成的脉冲信号数量得到实际转速值。快速录波仪采集脉冲频率，由脉冲频率和转子测速齿盘齿数在仪器内部计算得到转速值，当齿数为134 齿，脉冲频率为6700 Hz，转速为3000 r/min。调节汽阀反馈信号选取伺服卡输出。其他信号如油开关信号、电超速保护（Over Speed Protect Controller，OPC）信号、压力信号等要最大程度保证数据不失真且不延时。其中转子转速在测量过程中存在环境噪声及测量误差，并且转子在甩负荷扰动下出现的半速涡动[8]会对转速测量产生干扰，因此快速录波仪输出的转速信号并不能反映转子甩负荷过程中的真实转速。

2.3 100%甩负荷试验情况

机组带有功负荷346.43 MW，断开电气主开关，发电机解列，转速开始飞升，经过2.7 s 达到最高飞升转速3 142.5 r/min。当机组转速降至3 089.6 r/min时，OPC 电磁阀恢复，调节汽阀开启，转速维持在3000 r/min。100%甩负荷前后主要参数变化见表1。

3 数据分析与处理

3.1 转速信号分析

由傅里叶原理可知，任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。对转速信号进行傅里叶变换，数据采样率为1000 Hz。由图1（a）可知，转子在甩负荷的扰动下出现的半速涡动对转速测量产生了干扰，其频率略低于25 Hz。且振幅也小得多；转速曲线主要由低频分量组成，且存在一定的噪声。由图1（b）可知，甩负荷试验现场采集到的转速信号时而上升，时而趋平，时而下降，但是在调节汽阀尚未关闭时其驱动功率未发生变化。因此，对转速曲线不经过任何处理求取转子转动惯量，势必存在信号的干扰，使得计算结果误差偏大，偏离实际值。

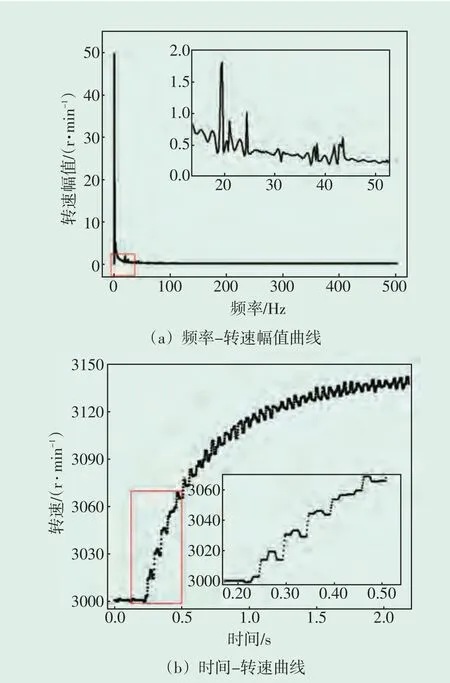
图1 某电厂350 MW机组甩负荷转速飞升曲线Fig.1 Speed soaring curve of load rejection of 350 MW unit in a certain thermal power plant

3.2 曲线平滑

叠加在有用数据上的随机噪声在很多情况下可以近似为白噪声，其统计平均值为零，因此可通过求平均值消除随机误差。移动平均滤波具有保低频滤高频的特点，而且对于特征频率的滤波具有良好效果。移动平均滤波的计算方法是将某点附近的采样点做算数平均，作为这个点平滑后的值：

3.3 转子最大加速度求解

3.3.1 S型函数

甩负荷后转速飞升可分为三个阶段：调节汽阀延迟关闭时间，进汽量Q保持不变，转速接近直线规律上升；调节汽阀关闭时间，进汽量Q 逐渐减小，转速继续上升，转子加速度逐渐减小；有害容积做功，转速飞升至最高转速，转子加速度逐渐趋于零。依据现场实测数据，转子转速飞升曲线符合S 型曲线增长模式：转折期转速增长最快；减速期转速增长逐渐变慢；饱和期转速增长趋于平稳，转速达到最大值。其拟合公式如下：

式中：x、y—被观测值；

Amax、Amin、x0、h、s—未知参数。

3.3.2 方法验证

利用上述方法对机组甩负荷试验数据进行2点移动平均滤波，对滤波数据利用S型函数及LM优化算法进行非线性最小二乘拟合，对拟合后的数据进行一阶微分处理，求解得到最大加速度。

为验证该求解方法的有效性与准确性，本文利用上述计算方法，对不同机组现场实测甩负荷试验转速飞升数据进行处理，其转速变化曲线及加速度曲线如图2所示。机组1与机组2为新建机组，型号分别为CJK350-24.2/566/566、CJK350/353-24.2/1.5/566/566；机组3 与机组4 为技改机组，型号为LZN-5.7/0.58，均按照导则要求开展甩负荷试验。图2（a）与图2（b）为机组1 的100%与50%甩负荷转速飞升曲线数据处理结果；图2（d）与图2（e）为机组3与机组4的100%甩负荷转速飞升曲线。由图2可知，转子最大加速度出现在转速飞升的初始阶段，且S型函数对转速飞升阶段的数据有很好的拟合效果，读取图2 一阶微分曲线最大值即为该机组转子最大加速度。

图2 不同机组甩负荷转速变化曲线及加速度曲线Fig.2 Variation curves of speed and acceleration during load rejection of different units

依据转子转动惯量计算原理，已知上述不同机组的发电机效率、甩负荷率、初始功率及转子最大加速度，由公式（2）及公式（1）可分别求得转子时间常数及转子转动惯量。上述不同机组的转子转动惯量设计值由厂家提供，其设计值与计算值的偏差如表2所示。

表2中数据为基于上述机组现场甩负荷试验实测结果及通过上述数据处理方法及计算求解得到的结果。机组1 对应不同的甩负荷率，其转子转动惯量计算值与设计值偏差分别为-0.473%、-1.42%；机组2 转子转动惯量计算值与设计值偏差分别为1.78%；机组3 与机组4 为同类型机组，转子转动惯量设计值无法查证，对比两台机组其转子转动惯量计算偏差为-2.06%。转子转动惯量计算值与实测值的计算偏差在很小的范围内。通过对不同机组甩负荷试验现场实测数据的处理及计算，进一步验证了上述方法的有效性与准确性。

3.4 对比分析

对上述电厂350 MW 机组进行数据处理，机组100%甩负荷转子最大加速度为414.315 r/（min·s），转子转动惯量为25 539.942 kg·m2。甩负荷试验导则中的计算方法要对转速飞升曲线进行平滑处理，再对处理后的数据采用调节汽阀延迟关闭时间范围内转速线性拟合的方法求取加速度。由图3 可知，以转速开始飞升的时间点为零点，数据采样间隔为0.001 s，选取不同的时间间隔进行线性拟合求解加速度，加速度值在170～694 r/（min·s），转动惯量计算值在15 326～62 403 kg·m2。

图3 某电厂350 MW机组甩负荷转速变化曲线及加速度曲线Fig.3 Variation curves of speed and acceleration during load rejection of 350 MW unit in a certain thermal power plant

汽轮机6个调节汽阀由于其自身特性延迟关闭时间不同，人工读取时间间隔进行转子转动惯量计算势必会出现千差万别的结果。而由表2中计算结果可知，采用S型函数及LM优化算法进行非线性最小二乘拟合求解最大加速度，与传统手工选取时间间隔计算转子转动惯量相比，其具有确定解，且与设计值较为贴合。

4 甩负荷试验过程动态仿真

以上述电厂350 MW 机组甩负荷试验为例，其调节系统相关技术参数见表3。转子时间常数Ta以表2中计算结果为准。为方便分析甩负荷试验过程中各种因素（包括甩负荷率、再热容积时间常数、转速偏差放大倍数等）引起的转速超调量及对甩负荷动态特性的影响，参照机组甩负荷时系统控制逻辑，建立机组甩负荷试验动态仿真模型，见图4。该模型主要由执行机构、原动机及转子模型构成[9-10]。

图4 机组甩负荷动态仿真模型Fig.4 Dynamic simulation model of unit load rejection

表2 转子转动惯量计算值Tab.2 Calculated value of rotor moment of inertia

表3 机组调节系统技术参数Tab.3 Technical parameters of unit regulation system

4.1 仿真模型验证

在MATLAB SIMULINK 仿真软件中设置仿真时长为87 s，给定负荷切除信号，机组100%甩负荷转速飞升实测结果与仿真结果对比如图5（a）所示，最高飞升转速为3 142.85 r/min，振荡最低转速2 968.5 r/min，与实测值偏差分别为0.011%和0.075%。OPC触发信号仿真结果与实测结果如图5（b）所示，OPC触发时间10.25 s。仿真结果与实测结果偏差很小，可验证上述模型有效。

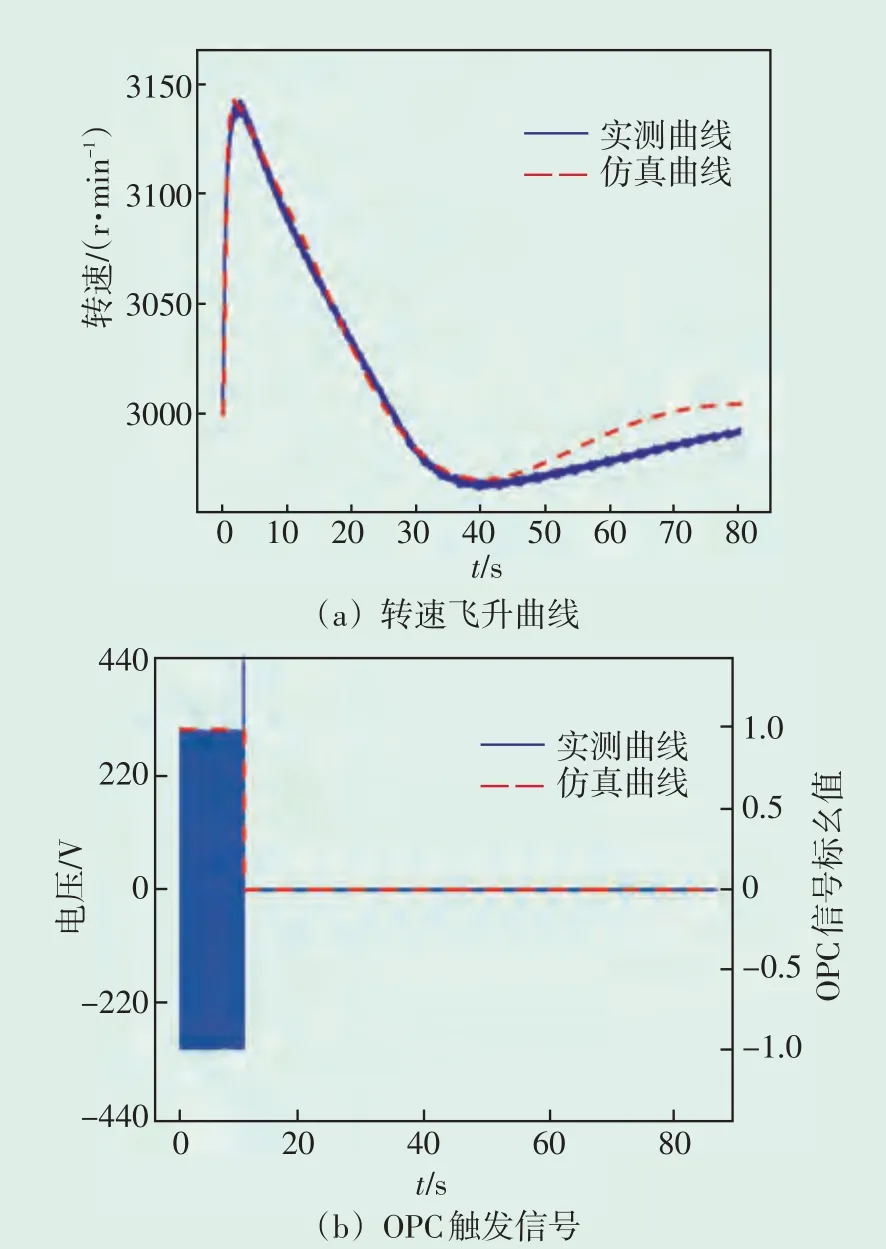
图5 100%甩负荷实测结果与仿真结果对比曲线Fig.5 Comparison curve between measured results and simulation results of 100% load rejection

4.2 仿真结果分析

4.2.1 甩负荷率λ对动态特性的影响

在此模型基础上，分别模拟机组不同工况下的甩负荷转速飞升曲线，如图6（a）所示。仿真结果表明，机组甩负荷率对最高飞升转速有很大影响，机组带高负荷运行时，进入汽轮机的蒸汽流量较大，蒸汽压力与温度更高，在调节汽阀延迟关闭时间内蒸汽所做的功越多，因此最高飞升转速值越大。随着机组运行负荷的减小，进入汽轮机的蒸汽流量减少，机组在甩负荷后能在更短的时间内恢复机组稳定，振荡最低转速也相应减小。

4.2.2 再热容积时间常数Trh 对动态特性的影响

在建模过程中发现，机组再热容积时间常数相比其他参数数量级较大，再热机组连接中间再热器的管道较长，温度压力分布不均匀，因此对机组不同再热容积时间常数进行仿真，仿真结果如图6（b）所示。结果表明，随着Trh的增大，机组甩负荷最高飞升转速将增大且转速飞升时间也相应延长，振荡最低转速相应减小。机组甩负荷过程中，中压调节汽阀如果控制不够严密，再热容积时间为8～10 s时，其最高飞升转速可达额定转速的1.5～2 倍[11-14]。因此，机组再热容积时间常数越小对机组甩负荷越有利。

图6 甩负荷动态特性仿真结果Fig.6 Simulation results of dynamic characteristics of load rejection

4.2.3 转速偏差放大倍数1/δ对动态特性的影响

转速偏差放大倍数对仿真结果影响如6（c）所示，转速不等率δ值越大，机组最高飞升转速值越大，振荡最低转速越小，且转速飞升特性对δ值非常敏感。机组转速不等率δ是调节系统的重要指标，但是δ过小，易引起调节系统不稳定，甚至引起调节系统震荡；相反δ过大，则不能保证供电频率在规定范围内。δ一般取4%～5%[15]。

5 结束语

本文对转速飞升曲线进行平滑处理及S型函数加LM优化算法进行非线性最小二乘拟合直接求解最大加速度，可以消除传统计算方法人工选取时间间隔造成的误差，提高计算精度。通过该方法计算的转子转动惯量与设计值或同类型机组相比偏差都在很小范围内。将OPC信号计入到数学模型中，利用上述模型可以方便分析汽轮机甩负荷过程，模拟甩负荷率、再热容积时间常数、转速偏差放大倍数等参数对转速飞升动态特性的影响，对不具备甩负荷试验条件的机组可提供模型参考。