致密裂缝储层双侧向测井侵入响应数值模型

吴进波,陈 鸣,许 巍,孙殿强,杨 冬,杨红斌

(1. 中海石油(中国)有限公司湛江分公司,广东 湛江 524057； 2. 长江大学 地球物理与石油资源学院,武汉 430100； 3.中国石油大学(华东) 石油工程学院,山东 青岛 266580)

0 引言

近年来,随着我国基岩和潜山成藏理论研究方面的理论创新及突破,基岩潜山油气储层成为了当前油气勘探的热点。我国在渤海湾盆地、塔里木盆地和准格尔盆地等地均勘探发现了潜山油气藏,揭示了潜山储层巨大的勘探潜力[1-2]。然而,潜山储层地层致密,裂缝发育复杂,如何利用测井资料准确评价储层裂缝参数是当前勘探开发的难点[3]。

花岗岩潜山储层测井数据相对较少,在研究裂缝储层测井响应特征时,数值模拟是最为基础和经济的手段。作为盐水泥浆条件下最经典的电阻率测井仪器,双侧向测井在油气储层识别及裂缝评价方面发挥了重要作用。国内外专家学者在裂缝储层中双侧向测井响应数值模拟方面做了大量研究。1985年,斯伦贝谢Sibbit A.M[4]等人基于有限元法提出了利用双侧向差异来估算高角度裂缝及低角度裂缝宽度的公式；1995年,汪涵明[5]等人采用平板裂缝模型计算了单一倾斜裂缝的双侧向测井响应,建立了利用双侧向测井深浅探测正负差异评价裂缝倾角的模型；1996年,李善军[6]等人采用平板裂缝模型,基于正演模拟结果,建立了基于双侧向测井深浅探测电阻率的裂缝孔隙度反演模型；2011年,卢春利[7]利用模拟缝洞模型中的双侧向测井响应特征,构建了缝洞地层中利用双侧向测井识别孔洞的方法。2014年,王小明[8]等人采用三维有限元素法对水平井网状裂缝储层模型储层的双侧向响应进行数值模拟,重点考察了网状裂缝中流体电阻率、基岩电阻率及裂缝倾角等因素变化所引起的响应特性；2019年,曹重[9]采用三维有限元素法对单一裂缝进行数值模拟,分析了双侧向测井响应随裂缝位置、裂缝产状的变化规律。然而,在传统模拟裂缝储层双侧向测井响应的文献中,大多数都只模拟了双侧向测井对各类裂缝参数的响应特征,较少对裂缝流体的侵入变化特征进行分析,而这对于实际油气储层评价至关重要。

该文基于一种改进的侵入平板状裂缝模型,建立了潜山裂缝储层双侧向测井三维有限元模型,分别模拟了高矿化度裂缝地层和高阻裂缝储层中双侧向测井响应,模拟结果可为潜山裂缝储层定性识别及半定量评价提供理论基础。

1 裂缝储层双侧向测井有限元建模

1.1 侵入裂缝地层数学模型

对于双侧向测井电阻率测量,裂缝发育地层表现为电阻率宏观各向异性,因此在研究裂缝影响时,可将其等效为经典的平板状模型[10]。如图1所示,在传统平板状裂缝模型中,σb和σf分别代表基岩电导率和裂缝流体电导率,hf为裂缝张开度,θf为裂缝倾角,d为裂缝间距。基于该平板状裂缝模型,当裂缝张开度hf足够小,裂缝流体电导率σf远小于基岩电导率σb时,裂缝表现为宏观各向异性[11]。

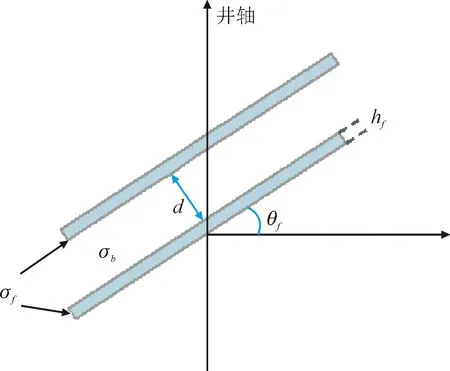
图1 平板状裂缝模型示意图Fig.1 Schematic diagram of parallel crack model

传统的平板裂缝模型中,裂缝流体大多为同一种流体,并未考虑井眼泥浆对裂缝流体侵入所造成的影响。该文基于井眼泥浆对不同裂缝流体的侵入情况,结合双侧向测井实际探测特性,建立了考虑侵入的平板状裂缝模型,如图2所示。

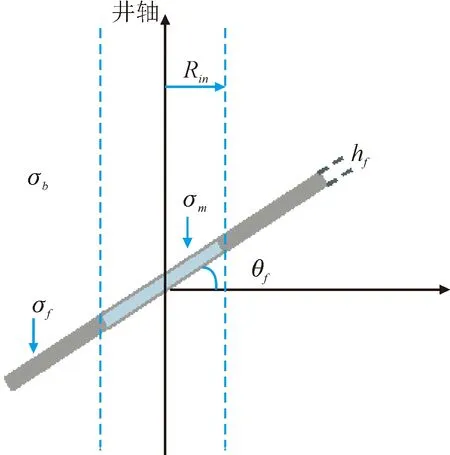
图2 侵入裂缝模型示意图Fig.2 Schematic diagram of invasion crack model

相对于传统无侵入平板状裂缝模型,该文所构建模型中原状地层流体电导率为σf,其电导率张量可表示为：

σ=

(1)

然而,在侵入深度范围Rin内的裂缝流体为井眼泥浆,其电导率为σm,对应侵入区域内的电导率张量为：

σ=

(2)

1.2 双侧向测井三维有限元建模

双侧向测井响应数值模拟的本质是求解地层中稳态电场的问题,其监督电极中的电位值可以分解为多个发射电极所产生分电场的叠加结果。根据有限元理论,若把分场中的电极记为A,则相应电位泛函极值问题可表示为[12]：

J(u)=

(3)

式中：σ为地层模型电导率;Γ为发射电极A的表面;IA为电极A的电流;UA为电极A的电位;Ω是计算求解域。

为求解式(3)中泛函极值,还需要联立以下模型边界条件[13-15]：在无穷远边界上满足第1类边界条件；在电极表面的绝缘环和对称轴边界上满足第2类边界条件；在电极表面满足等位面条件；在不同电阻率区域交界面满足电位连续条件。

通过边界条件约束即可求解获得单个发射电极的电场分布,进而通过电场叠加方法计算得到双侧向测井视电阻率值。

2 不同侵入条件裂缝储层双侧向测井数值模拟

2.1 高矿化度水层裂缝侵入特征模拟

高矿化度水层裂缝侵入模拟采用的地层参数如下：基岩电阻率Rt=10 000 Ω·m,泥浆电阻率Rm= 0.1 Ω·m,地层裂缝流体电阻率Rf= 0.01 Ω·m,裂缝张开度为200 μm。由于双侧向测井仪器实测电阻率曲线会经过自动井眼校正,因此井眼影响可以忽略,文中仅考虑泥浆对高矿化度裂缝流体侵入的影响。

为研究不同倾角裂缝在不同侵入程度的双侧向测井响应,文中选取了0°,45°和90°倾角3种不同裂缝(水平缝、45°缝和垂直缝),模拟了侵入深度为10～1 000 cm的双侧向测井响应,如图3所示。

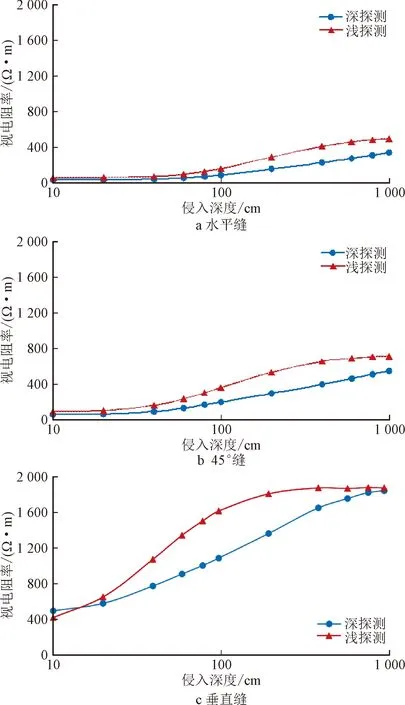
图3 不同裂缝侵入深度高矿化度水层双侧向测井响应Fig.3 Dual laterolog response of high salinity water layer with different fracture invasion

在高矿化度地层模型中,低阻裂缝流体容易形成优势导电通道,当侵入的泥浆电阻率Rm大于地层流体电阻率Rf时,随着侵入深度加深,裂缝导电性逐渐变弱。

如图3a所示,在水平裂缝模型中,在侵入深度较浅时,深浅探测电阻率差异较小,随着侵入深度增大,深浅探测电阻率差异逐渐增大；如图3b所示,在45°倾角裂缝模型中,同等侵入深度条件下,深浅探测电阻率值明显大于水平裂缝模型中的模拟值,侵入深度变化所引起的视电阻率变化比水平裂缝模型更加明显；如图3c所示,在垂直裂缝模型中,随着侵入深度的增大,浅探测电阻率增大最为明显,但当侵入深度达到200 cm时,浅探测电阻值对侵入深度变化不敏感,最终在侵入深度达到1 000 cm时,深浅探测电阻值接近。

对比而言,在高矿化度地层模型中,同等侵入条件下,随着裂缝倾角增大,双侧向受裂缝流体电阻率影响变小,深浅探测视电阻率值更加接近基岩电阻率值。由于深探测聚焦能力强于浅探测,深探测视电阻率值对裂缝流体侵入变化更加敏感。

2.2 油气层裂缝侵入特征模拟

高阻油气储层裂缝侵入模拟采用的地层参数如下：基岩电阻率Rt=10 000 Ω·m,泥浆电阻率Rm= 0.1 Ω·m,地层裂缝流体电阻率Rf= 1 000 Ω·m,裂缝张开度为200 μm。为研究不同倾角裂缝在不同侵入程度的双侧向测井响应,文中选取了0°,45°和90°倾角3种不同裂缝(水平缝、45°缝和垂直缝),模拟了侵入深度为10～1 000 cm的双侧向测井响应,如图4所示。

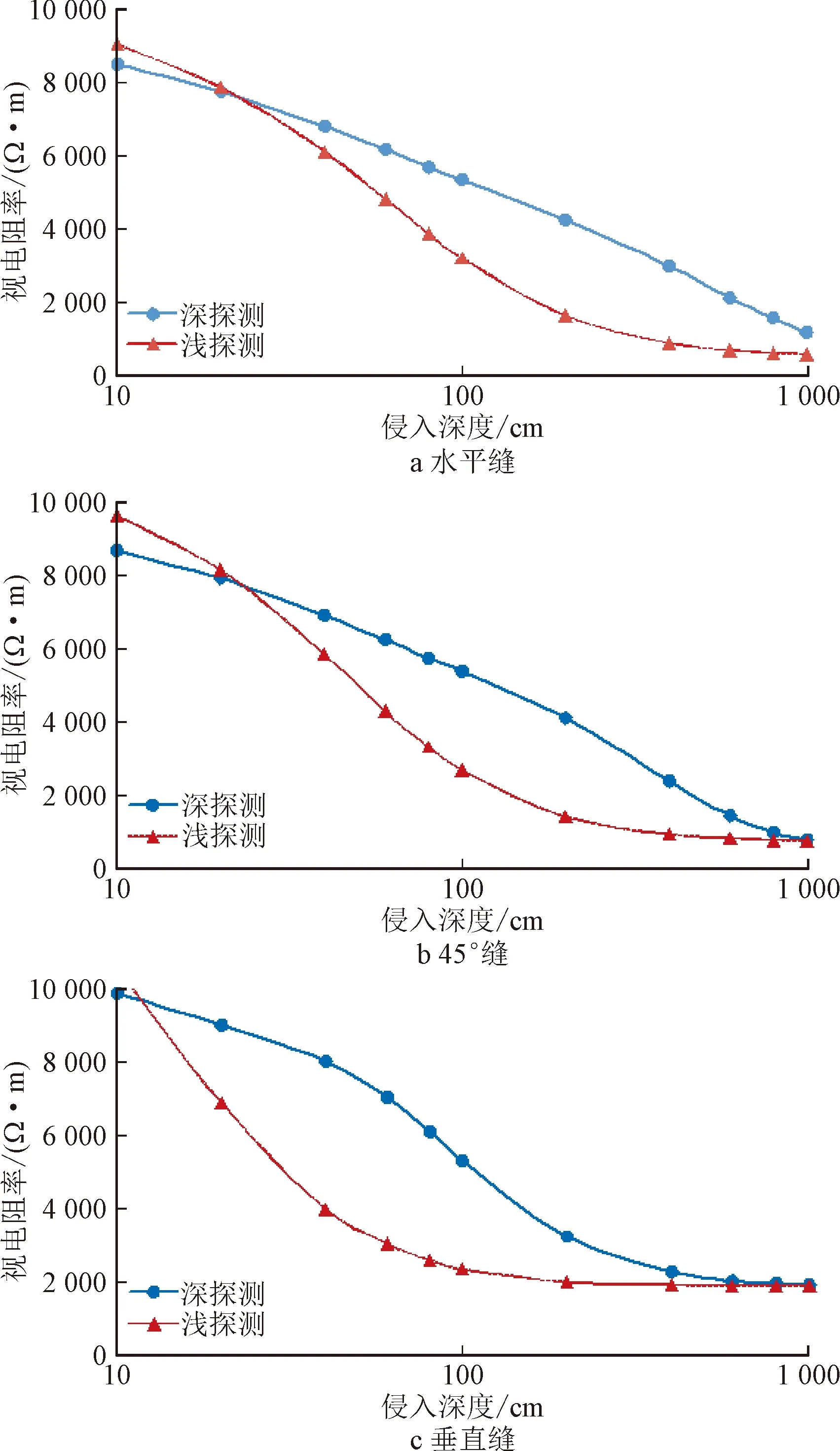
图4 不同裂缝侵入深度油气层双侧向测井响应Fig.4 Dual laterolog response of reservoir with different fracture invasion depth

在高阻油气储层中,原状裂缝流体一般为高阻,当侵入的泥浆电阻率Rm小于地层流体电阻率Rf时,随着侵入深度加深,裂缝导电性逐渐变强,裂缝逐渐形成优势导电通道。

如图4a所示,在水平裂缝模型中,在侵入深度较浅时,深浅探测电阻率差异较小,随着侵入深度增大,深浅探测电阻率差异逐渐增大,且浅探测视电阻率值小于深探测视电阻率值；如图4b所示,在45°倾角裂缝模型中,同等侵入深度条件下,侵入深度变化所引起的视电阻率变化比水平裂缝模型更加明显；如图4c所示,在垂直裂缝模型中,随着侵入深度的增大浅探测电阻率减小的最为明显,但当侵入深度达到200 cm时,浅探测电阻值对侵入深度变化不敏感,最终在侵入深度达到1 000 cm时,深浅探测电阻值接近。

对比而言,在高阻油气储层模型中,同等侵入条件下,随着裂缝倾角增大,双侧向受裂缝流体电阻率影响变小,深浅探测视电阻率值更加接近基岩电阻率值。由于深探测聚焦能力强于浅探测,深探测视电阻率值对裂缝流体侵入变化更加敏感。

3 结论

1)基于裂缝地层宏观各项异性电导率张量,建立了考虑泥浆侵入的裂缝储层双侧向测井三维有限元模型。相对于传统的平板状裂缝模型,文中裂缝模型不仅考虑泥浆侵入深度的影响,还考虑了不同裂缝流体被泥浆侵入的电导率变化,具有更加实际的应用价值。

2)利用所构建的裂缝模型,分别开展了高矿化度裂缝流体及高阻裂缝流体被低阻盐水泥浆侵入时的双侧向测井响应模拟。模拟结果表明,在高矿化度地层模型中,双侧向测井深浅探测视电阻率值呈“负差异”,在高阻油气储层模型中,双侧向测井深浅探测视电阻率值呈“正差异”；随着泥浆侵入深度的增大,双侧向测井深浅探测视电阻率值差异先增大后减小；随着裂缝倾角增大,裂缝影响逐渐减小,双侧向测井深浅探测视电阻率值逐渐增大。对比而言,深探测值对泥浆侵入更加敏感。

3)文中数值模拟结果为利用双侧向测井评价潜山储层裂缝提供了理论基础和模型基础。然而由于该模型裂缝模型较为简单,且未考虑裂缝密度等参数的影响,其应用效果有待进一步的研究和论证。