磨矿动力学研究现状及应用

田鹏程，王泽红，毛 勇

(东北大学资源与土木工程学院，辽宁 沈阳 110819)

磨矿作业在冶金、陶瓷、建筑、水泥、化工、医学甚至国防工业领域都占据极其重要的地位，尤其是矿物加工工程领域。有用矿物实现有效分选的前提是其与脉石矿物得到充分的单体解离，而这主要通过粉磨作业完成[1-3]。值得注意的是，粉磨过程是一个能耗和钢耗很高、效率偏低的作业，特别是在细磨和超细磨时表现得更加突出，因此，磨矿作业在选矿厂的基建投资和生产费用中占比很大[4-5]。为节约能耗、降低磨矿钢耗、提高磨矿效率，相关研究者一方面通过数学工具(数学模型)分析磨矿过程颗粒粒度及其组成的变化规律，另一方面从物理化学角度探究影响磨矿过程的因素(矿物界面性质和矿浆性质)，不断寻求改善磨矿工艺的有效手段[6]。

磨矿动力学模型是描述被磨物料的磨碎速率与磨矿时间之间关系规律的一种模型。通过磨矿动力学能够研究粒度减小的规律，计算磨机的效率和生产率，并对实际磨矿过程做出理论分析。随着选矿生产过程最优化、模拟计算及自动控制技术的应用和推广，磨矿动力学已逐渐成为矿物加工领域，特别是粉磨领域的重点研究方向之一[7-8]。为进一步推动磨矿动力学模型在矿物加工领域的研究与应用，本文系统综述了磨矿动力学的两个经典模型：m阶磨矿动力学模型(m≥0)及磨矿总体平衡动力学模型，以及影响磨矿动力学的主要因素，指出了磨矿动力学模型的应用现状及发展趋势，并据此提出展望。

1 m阶磨矿动力学模型

在矿物加工过程中，存在两大类动态模型：①模拟自动控制技术调节的正常工艺过程(存在外界干扰)的动态模型；②工艺过程正常进行时各项指标随时间变化的动态模型，即动力学模型[9]。在磨矿过程中，磨矿产品粒度分布随时间变化的关系可用m阶磨矿动力学模型来描述[10]。

Ri(t)=Ri(0)e-ktm,i=1,2,3,…,j

(1)

式中：t为磨矿时间，min；Ri(0)、Ri(t)分别为给料和产品中大于粒级i的颗粒的累积产率，%；j为给料或产品的窄粒级数目；k、m为与物料性质和磨矿条件有关的参数，k、m与粒度d的函数关系分别见式(2)和式(3)。

k(d)=A0+A1dX1

(2)

m(d)=C0+C1dX2

(3)

式中，A0、A1、C0、C1、X1、X2为待定的参数。

对式(1)而言，当m=0时，为零阶动力学模型；当m=1时，为一阶动力学模型。

对于参数k和m的理论意义，段希祥[11]曾用石英、方解石和重晶石分别进行粗磨和细磨试验，建立了m阶磨矿动力学方程，指出了动力学参数k、n的数值在不同磨矿阶段(即物料粒度不同时)的变化能反映磨矿过程的实际情况，对早期苏联学者的解释进行了修正，并结合试验与模型对参数的意义和相互关系进行了解释：m主要反映物料性质的均匀性，而与物料的强度几乎无关；k与磨矿粒度、物料性质以及磨矿条件有关。侯英等[12]在段希祥[11]的研究基础上，采用解析几何和偏导数的方法对m阶磨矿动力学参数k和m进行研究，分析了k和m与磨矿时间t的关系以及对磨矿速度的影响规律：当磨矿时间t≪e1/k时，k对筛上累积产率R起主要影响作用，k越大，R越小，R减少的越多，磨矿速度越快；当t≫e1/k时，m对R起主要影响作用，m越大，R越小，R减少的越多，磨矿速度越快；当t在e1/k附近时，k和m共同影响R的减少和磨矿速度。LIU等[13]对石英进行分批球磨试验，推导得出了石英粉磨动力学方程，结果表明：该磨矿动力学方程与理论的一阶动力学方程不一致，其动力学参数k并非常数，而是与时间有关的变量，且变化规律与物料性质、磨矿条件和产品粒度分布有关。

因此，关于m阶磨矿动力学模型参数k、m的研究，段希祥[11]和侯英等[12]的试验结果分别适用于参数与被磨物料粒度和磨矿时间的关系研究，LIU等[13]的研究结果只适用于参数k与物料性质和磨矿时间的关系研究。

2 磨矿总体平衡动力学模型

2.1 磨矿总体平衡动力学模型

1954年SEDLATSCHEK等[14]提出了物料研磨过程的数学理论，首次采用积分微分方程的形式表示批量研磨的基本质量平衡。该动力学模型根据物料平衡原理建立，在分批磨矿过程中，既没有物料加入也没有物料排出，这时某个指定粒级在磨机内的变化速率等于生成速率减去消失速率，综合矩阵模型和磨矿动力学，即可得到分批磨矿时间连续、粒度离散的总体平衡动力学模型[15]，见式(4)。

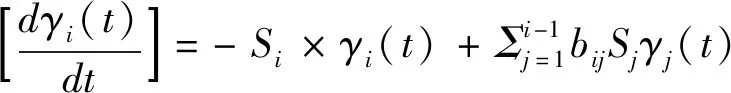
(4)

总体平衡动力学模型的矩阵形式见式(5)。

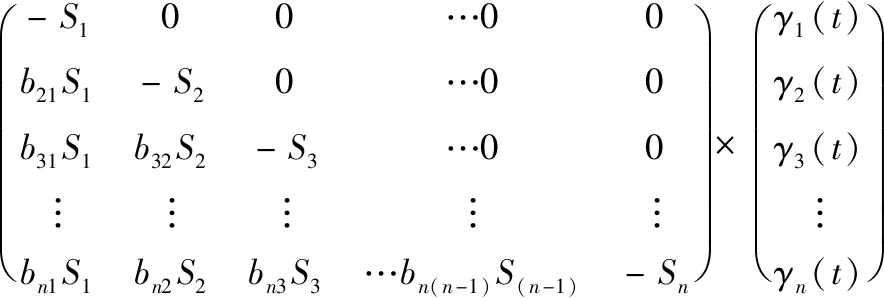
(5)

式中：γi(t)为t时刻第i粒级的含量(产率)，%；Si为破碎速率函数(选择函数)，min-1；bij为破裂分布函数，%，表示从给料第j粒级粉碎至产品中第i粒级的产率，i=1，2，3，…，n；j=1，2，3，…，n(i>j)。为便于表述和计算，总体平衡动力学模型中的破碎分布函数bij常用累积破碎分布函数Bij(破裂函数)表示，见式(6)。

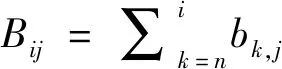
(6)

式中，Bij为给料中第j粒级破碎后形成的产品中小于i粒级的累积产率。

2.2 模型的分析解

1965年REID[16]在一定假设的前提下，以试验为基础，通过积分微分方程方法，结合总体平衡方程推导出了物料破碎速率函数Si(选择函数)和破碎粒度分布函数Bij(破裂函数)，并给出了式(4)的分析解。

当式(4)中i=1时，总体平衡动力学方程变为微分方程，见式(7)。

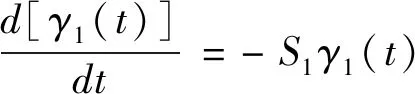
(7)

对式(7)进行求解，其结果见式(8)。

lnγ1(t)=-S1t+C

(8)

当式(8)中t=0时，可求得参数C=lnγ1(0)，则式(8)存在唯一确定解，见式(9)。

lnγ1(t)=-S1t+lnγ1(0)

(9)

对式(9)等号两边同时求指数，其结果见式(10)，表示在t时间磨矿产品中第1粒级的产率γ1(t)与给料中第1粒级产率γ1(0)之间的关系。

γ1(t)=γ1(0)×e-S1t

(10)

式中：S1为第1粒级的选择函数，min-1；t为磨矿时间，min。

当式(4)中i=2时，总体平衡动力学方程可转化为微分形式，见式(11)。

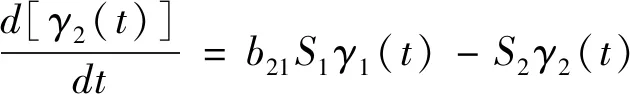
(11)

式(11)为一阶微分方程式，其通解见式(12)。

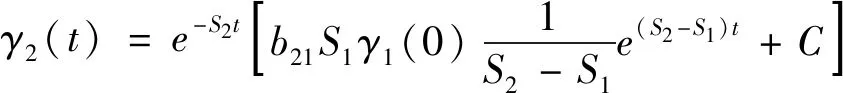
(12)

令式(12)中t=0时，可得参数C的表达式，见式(13)。

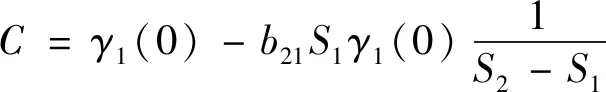
(13)

将式(13)代入式(12)，可得到微分方程解的表达式，见式(14)。

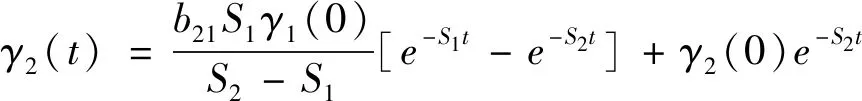
(14)

当式(4)中i=2时，总体平衡动力学方程变为一阶微分方程，见式(15)。

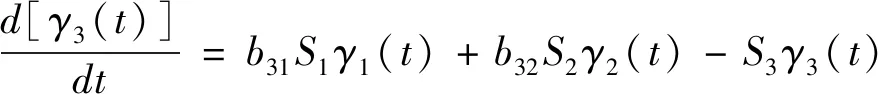
(15)

同样利用一阶微分方程的公式对式(15)进行求解，可得到γ3(t)的通解，即式(4)或式(5)的通解，见式(16)。

(16)

将式(16)的矩阵形式用求和符号表示，见式(17)。

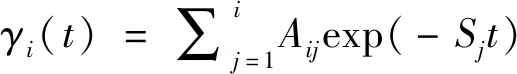
(17)

式(17)中系数Aij的计算见式(18)。

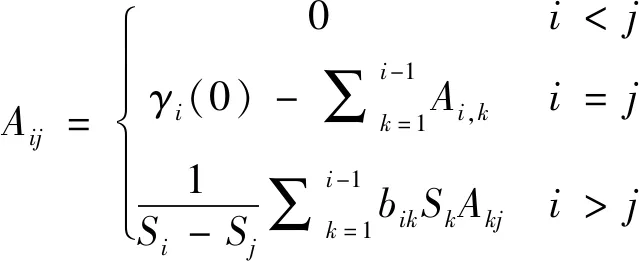
(18)

式中，γi(0)为磨机给料中第i粒级的含量，%。对于最粗粒级物料或者窄粒级别单粒级物料磨碎时，即第一粒级物料i=1，式(4)或式(5)的简化形式见式(19)。

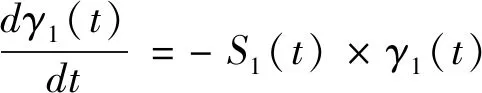
(19)

式中：γ1(t)为t时刻第一粒级的质量分数(产率)，%；S1(t)为第一粒级的破碎速率函数(选择函数)，min-1。当破碎速率函数S1与磨矿时间无关，即物料的磨矿过程符合一阶线性动力学模型时，对于单粒级物料可知γ1(0)=1，将式(19)积分求解，可得到常见的一阶磨矿动力学方程，见式(20)。

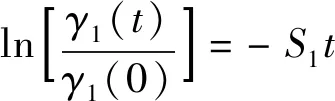
(20)

由式(20)可知，磨矿t时刻的试验结果γ1(t)的对数值与时间t为直线关系，该直线的斜率即为破碎速率函数S1。

2.3 选择函数和破裂函数

求解式(4)或式(5)时，必须先求得选择函数Si和破裂函数bij。Si和bij的求法有很多，一般需要根据具体矿物和作业条件进行试验，然后根据试验数据计算。常用方法有零阶产出率法、奥-勒(Austin和Luckie)理论简算法(又称预估-反算法)、卡普尔(Kapur)的G-H算法、经验公式法以及理想混合器模拟算法等[17-19]。

2.3.1 零阶产出率法

零阶产出率法由赫尔伯斯特和富尔斯坦诺(Herbst &Fuerstenau)提出，其出发点是假定磨矿速率为常数，见式(21)。

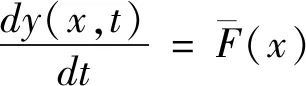
(21)

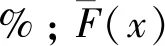
假定速度常数的表达式见式(22)。

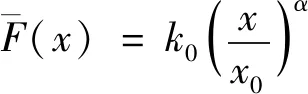
(22)

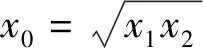
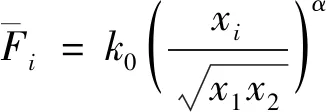
(23)

式中，i=1,2,…,n(n为物料粒级数)。

将每个速度常数表达式依次列出，见式(24)。

……………

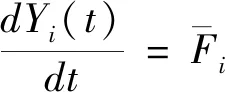
(24)

将yi(t)离散化，即以窄级别产率yi(t)之和表示，见式(25)和式(26)。

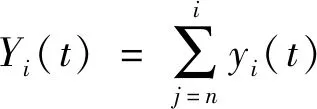
(25)

…+bn1S1y1(t)+b32S2y2(t)+b42S2y2(t)+

…bn2S2y2(t)+b43S3y3(t)+b53S3y3(t)+

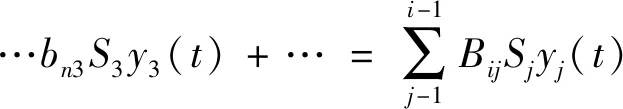
(26)

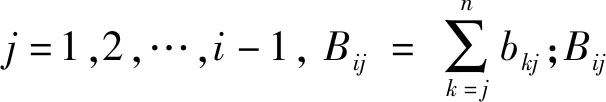
当磨矿时间较短时，细粒级产品符合的关系见式(27)。

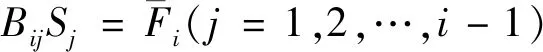
(27)

将式(27)代入式(26)可得Yi(t)与t的微分关系，见式(28)。

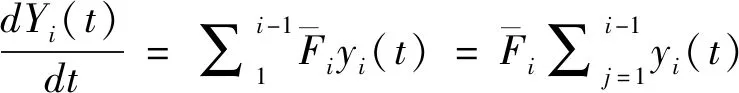
(28)

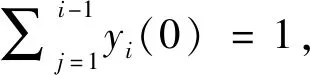
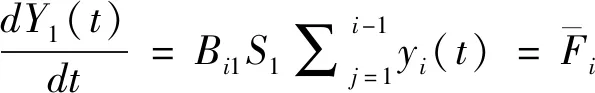
(29)

由式(22)和式(27)可得最粗粒级的破碎分布函数，见式(30)。

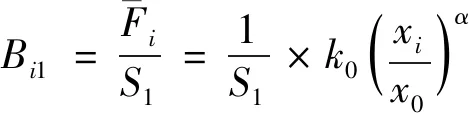
(30)

由式(27)可得最粗粒级的破碎速率函数和破碎分布函数的关系，见式(31)。

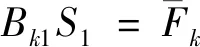
(31)

将式(31)进行整理，见式(32)。

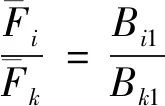
(32)

由式(30)和式(32)得到破碎分布函数与物料粒级关系，见式(33)。

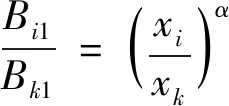
(33)

若破裂函数是规范化的，则可求得破碎分布函数和破碎速率函数的表达式，见式(34)和式(35)。

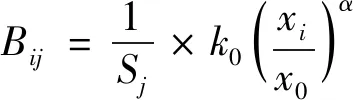
(34)

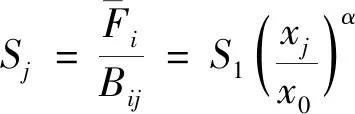
(35)

2.3.2 奥-勒法

奥-勒法[20-21]又称预估-反算法，这种算法1972年由AUSTIN等提出，以单粒级物料短时间磨矿试验的数据为基础来推导选择函数和破裂函数。进行单粒级不同磨矿时间试验后，根据一阶动力学方程求不同粒度的Si；求出S值后反算B的值。求B值有三种方法，即BⅠ法、BⅡ法、BⅢ法，其中BⅡ法使用最为广泛。具体方法如下所述。

原物料为单粒级，将其进行再次筛分得到筛下产率，见式(36)。

γ2(0)=σ

(36)

式中，σ为筛分误差，即原单粒级物料未筛分完全的剩余细级别含量，小数。

与零阶产出率法的假设相同，破碎分布函数与破碎速率函数的乘积为累积产率速度常数，见式(37)。

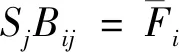
(37)

由一阶动力学方程得到i粒级的筛下累积产率表达式，见式(38)。

[1-pi(0)]exp(-SjBijt)

(38)

式中，pi(t)为产品中小于i粒级的累积产率，小数。

同样假设磨矿时间很短，无重复破裂，则原单粒级物料破裂后产物的筛下累积产率可表示为式(39)。

1-pi(t)=[1-pi(0)]exp(-SjBijt)

(39)

假定t=0时，原给料单粒级分布为(1-σ)，即产率为1减去少量的细粒级别σ，即p2(0)=σ。对于第2粒级(i=2)，筛下累积产率的表达式见式(40)。

1-p2(t)=[1-σ]exp(-S1t)

(40)

对式(40)等号两边取对数整理后得到对数表达形式，见式(41)。

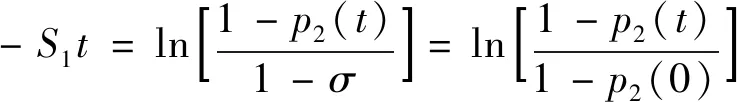
(41)

由式(38)可得到i粒级的破碎分布函数、破碎速率函数与筛下累积产率的关系，见式(42)和式(43)。

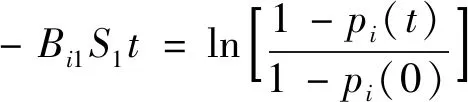
(42)

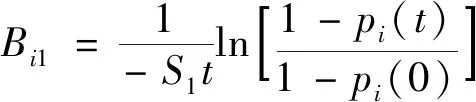
(43)

将式(41)代入式(43)得到i粒级的破碎分布函数表达式，见式(44)。

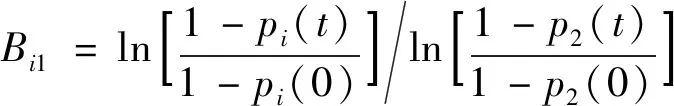
(44)

若假定破裂函数值是规范的，则求出Bi1后即可得出(i=1，2，3，…，n；j=1，2，3，…，i-1)。根据Bi1求解Bij的过程见式(45)。

Bij=Bi+1，j+1=B(i-j+1),1

(45)

式中，根据Bij的定义可知B11=1，B21=1。

2.3.3 G-H算法

该算法于1982年由卡普尔提出[22]，其基本指导思想是将总体平衡动力学方程式转换成G、H两个函数，使之能迭代运算，以便于计算机求解参数S、B的数值。该方程的推导过程较繁琐，本文给出主要求解步骤如下所述。

G-H算法方程见式(46)。

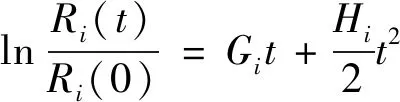
(46)

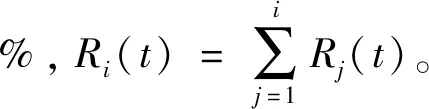
当原料为单粒级时，由式(46)得到系数函数Hi与破碎分布函数、破碎速率函数的关系，见式(49)。

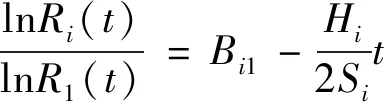
(49)

通过式(49)进行线性回归分析求得Bi1值，从而根据式(45)求得Bij值。

2.3.4 经验公式法

关于求解选择函数S、破裂函数B的经验公式较多，AUSTIN[23]和JIHOE等[24]提出的经验公式应用最为广泛，其是根据提纯矿物或均质物料试验结果所计算的，例如石英、石灰石、白云石、赤铁矿、无烟煤、金矿石、水泥熟料等。

对于干式磨矿，破碎速率函数表达式见式(50)。

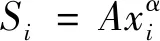
(50)

对于湿式磨矿，破碎速率函数表达式见式(51)。

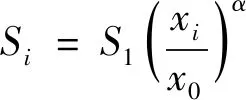
(51)

式中，A、α为参数。对于规范化的破裂函数B中的元素可用经验公式(式(52))求得。

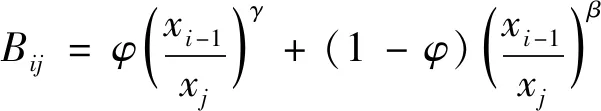
(52)

式中，φ、γ、β均为参数，其中，γ、β分别为Bij=f(x)曲线的两个斜率，φ为斜率为γ的直线与最大相对粒度的交点相应的Bij值。一般来说，这些参数与矿物粒度、磨矿时间等磨矿条件无关，对磨机矿浆充填率、球径或磨机内径也不敏感。

2.3.5 总体平衡动力学求解方法分析

总体平衡动力学方程是动力学模型与矩阵模型相结合的模型，通过对相关学者前期试验的研究，总结了其破碎速率函数和破碎分布函数的几种求解方法的特点和适用性，见表1。

表1 各求解方法特点与适应性Table 1 Characteristics and adaptability of solution methods

3 影响磨矿动力学的因素

磨矿是一个十分复杂的物理化学变化过程，磨矿效率受许多因素影响，这些因素在磨矿过程中使矿物颗粒性质和矿浆性质发生不同的变化，从而影响磨矿动力学模型参数[25-26]，各影响因素见表2。

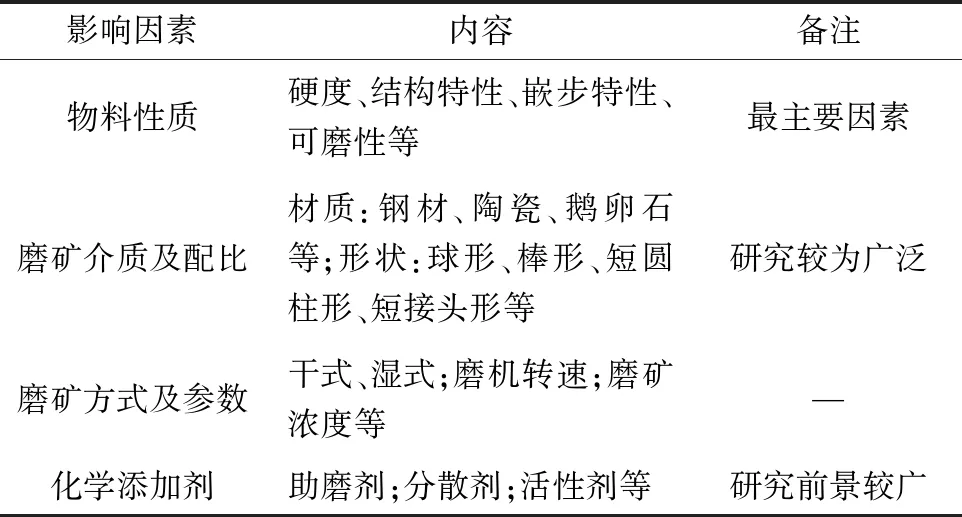
表2 磨矿动力学影响因素Table 2 Effecting factors of grinding kinetics

3.1 物料性质

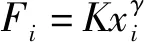
3.2 磨矿介质及配比

磨矿介质对磨矿动力学的影响也十分重要。在磨矿过程中，介质与物料、介质与介质、介质与衬板之间的相互作用会影响产品粒度。磨矿介质的材质比较多，主要包括钢材、陶瓷、鹅卵石等材质；介质的形状主要包括球形、棒形、短圆柱形、短截头锥形等[32]。QIAN等[33]在实验室规模球磨机中，利用直径为20 mm的钢球和20 mm×20 mm的圆柱形介质对水泥熟料进行粉磨试验，并比较了两种介质下的破碎速率函数和破碎分布函数后发现：两种介质下水泥熟料产品粒级均符合一阶磨矿动力学模型，并且圆柱形介质的破碎函数Si大于钢球，得出了这两种介质下的最佳给料尺寸为-2.00+1.77 mm，即此情况下破碎函数Si最大。李同清等[34]在三种研磨介质(钢球、钢段和立方体)下对四个单粒级的铁矿石进行磨矿试验，建立了m阶磨矿动力学模型，探究了磨矿动力学参数k和m，比较了三种磨矿介质下的比破碎速率：磨矿动力学参数k和m在钢球介质下始终最大，在钢段介质下始终最小；随着给料尺寸的增大，三种磨矿介质下的比破碎率先增大后减小，而且钢球介质下的比破碎率最大，立方体介质下的比破碎率最小。吴桂义等[35]采用直径为40 mm、30 mm和20 mm的三种钢球研究了介质配比对铁矿石磨矿动力学的影响研究得出：铁矿石不符合一阶磨矿动力学，比破碎率随着磨矿时间的增加而减小，介质配比(质量比)为Φ40∶Φ30∶Φ20=1∶1∶1时，对各种给料粒度的矿石磨矿效果均较差；对于-13.2+9.5 mm和-6.70+4.75 mm粒级矿石，配比为3∶1∶1时的磨矿效果优于其他配比。

3.3 磨矿方式及参数

磨矿方式、磨机转速、磨矿浓度等都是影响磨矿动力学行为的重要因素[36]。OZKAN等[37]利用实验室球磨机对沸石进行了湿磨和干磨试验，建立了单粒级的m阶磨矿动力学方程和累积分布函数表达式，并分析比较了干磨和湿磨的破碎函数S和分布函数B的差异：单粒级沸石湿磨和干磨均符合一阶磨矿动力学模型，在正常研磨区域湿磨的S值比干磨的S值高1.7倍，湿磨的Bi,1值与干磨近似相同，这充分说明了沸石在湿磨条件下能够产生更多的细粒级产物。叶贤东等[38]研究了球磨机在不同转速下的m阶磨矿动力学模型，并求出当磨机转速分别为120 r/min、150 r/min、180 r/min、200 r/min、240 r/min，磨矿时间分别为3 min、6 min、9 min、12 min时，待磨粒级(d=+74 μm)在t时刻的筛上累积产率R(t)。结果表明：当磨矿时间相同时，R(t)随磨机转速的增大而迅速下降，转速越大，这一趋势越明显；当磨机转速相同时，R(t)随磨矿时间的增大而减小，时间越长趋势越缓慢。周意超等[39]对湖南柿竹园某矿石进行了60%、65%、70%、75%和80%磨矿浓度下的两段磨矿试验，通过建立m阶磨矿动力学模型表示了磨矿产品粒级分布情况：当第一段和第二段磨矿浓度分别为75%和65%时，磨矿产品的粒度特性和能耗综合指标为最佳。

3.4 化学添加剂

在磨矿过程中，为了改善磨矿环境或物料表面的物理化学等方面特性，往往会加入助磨剂、分散剂等化学添加剂，从而导致磨矿动力学参数发生变化[40]。王力等[41]研究了煤沥青在MC(萘系磺酸盐)、AZMN(自制的改性α-甲基萘磺酸盐甲醛缩合物)两种助磨剂作用下的磨矿动力学方程式，分析了其研磨特性，确定了煤沥青水浆制备的磨矿工艺参数，并得出了两种助磨剂作用下任意时刻任一粒级的分布率。HEEKYU等[42]采用搅拌球磨机对方解石进行超细粉碎试验，研究了助磨剂添加对物料比表面积、研磨效率、粉碎系数k的影响，发现添加助磨剂的物料比表面积和粉碎系数k相对于不添加药剂分别增加了16%和34%，充分说明了助磨剂对磨矿的优化效果。黄勇等[43]研究了水泥在TEA和TIPA两种单体助磨剂作用下的磨矿动力学，发现水泥的比表面积与粉磨时间的平方根符合很好的线性关系，且加入TEA或TIPA后，水泥的比表面积大幅提高；高掺量TIPA对表面积和粒级分布的改善效果优于TEA。谢冬冬等[44]研究了NM-3、油酸钠、六偏磷酸钠、氟硅酸钠、乙酸铵和羧甲基纤维素钠对氧化铁矿石的磨矿动力学，通过建立m阶磨矿动力学方程，应用均匀实验设计方法确定了助磨剂最佳用量和配比并比较了不同种类助磨剂作用下各个粒级的磨矿效果。研究发现：添加乙酸铵和NM-3既增加了粗粒级颗粒的可磨性，又改善了矿浆流变性，从而显著提高粗粒级和细粒级的磨矿速度。

4 磨矿动力学的应用及发展趋势

目前，磨矿动力学的研究成果主要应用于以下几方面。一是改进、更新破碎设备及工艺。通过不同破碎方式及其产品的差异研究磨矿动力学及其参数的变化规律，从而确定适宜的破碎设备和工艺[45]。二是确定磨矿设备及磨矿方式。通过不同磨矿设备及磨矿方式对磨矿动力学的影响，为磨矿工艺提供指导[46]。三是确定磨机规格。通过计算机模拟不同规格磨机的磨矿过程，利用磨矿动力学模型分析其产品质量，为确定适宜磨机规格提供依据[47]。四是磨矿产品粒度的模拟计算，预测磨矿产品的粒度特性。五是确定适宜的磨矿条件，如磨机转速、介质尺寸及配比、磨矿浓度等。通过分析不同磨矿条件下的磨矿动力学参数的变化规律，确定适宜的磨矿条件[48]。六是分析磨机生产率与磨矿细度的关系。通过研究物料细度对磨矿动力学模型中与磨机生产率相关参数的影响规律，确定适宜的进料细度[49]。七是分析磨矿过程机理。通过将磨矿效率、磨机做功、受力分布等因素与磨矿动力学模型相结合，从粒度分布、能耗和受力等角度分析磨矿机理[50]。

磨矿动力学模型研究发展趋势主要有以下几方面。一是新型的参数求解方法。磨矿动力学模型参数的求解方法有多种，但随着经济社会的发展，步骤冗长、精确度低的计算方法越来越难以满足试验研究与实际生产，更加精确快速的求解方法需要被挖掘。二是化学添加剂的影响研究。物料性质、磨矿介质、方式及参数等因素对磨矿动力学的影响规律已得到很好的揭示，而化学添加剂对物料表面特性和矿浆性质会产生不同的作用，从而对磨矿动力学模型参数的影响规律存在差异，因此，化学添加剂与磨矿动力学模型的结合应当被予以重视。三是更加深入地研究磨矿参数对磨矿动力学的影响规律，进而明晰磨矿机理、改善磨矿产品、节约能耗钢耗。目前针对不同影响因素下的磨矿动力学参数变化规律已进行了大量的试验研究，但仍未建立适用于大多数磨矿过程的较为完整的磨矿动力学模型体系，因此，需要进一步探究磨矿参数对磨矿动力学模型的影响规律，为改善磨矿工艺提供理论基础。四是应用范围拓展。将磨矿动力学模型应用于可可豆、红葡萄籽、黑胡椒籽、玉米秸秆等食品的研磨加工过程中，并达到了预期的结果，可以预测，磨矿动力学模型将在生活、农业、工业生产中得到更加广泛的应用。

5 结论及展望

1) m阶磨矿动力学模型是粒度分布与时间及其相关量的动力学方程，该模型中存在参数m和k，m主要反映物料性质的均匀性，与物料的强度几乎无关，k与磨矿粒度、物料性质以及磨矿条件有关；在粗磨和细磨情况下，m和k分别有不同的变化规律。

2) 总体平衡磨矿动力学模型中包含破碎速率函数S和破碎分布函数B。关于S和B常用的求解方法主要有零阶产出特征法、G-H算法等。零阶产出特征法和BⅡ法作为G-H算法的特殊情况，使用条件是单粒级矿物短时间内的磨矿速率为常数，经验公式法对于不同矿物求解的误差较大。

3) 磨矿过程中，物料性质、磨矿介质、磨矿方式及参数和化学添加剂等因素对磨矿动力学的影响十分明显。通过研究这些影响因素，能够探究建立更加切合实际磨矿的动力学模型，改善磨矿产品，尤其是化学添加剂与磨矿动力学的结合，值得被关注研究。

4) 磨矿动力学模型在矿物加工领域已开展了许多相关试验研究且有广泛应用，今后在磨矿动力学参数求解、磨矿参数对磨矿动力学的影响以及化学添加剂对磨矿动力学参数影响等方面仍需加大研究力度。