基于实测模型的围框式翼身对接位姿优化

杜坤鹏，郑 炜，李泷杲，牛 振，彭 云

（1.中航西安飞机工业集团股份有限公司，西安 710089；2.南京航空航天大学，南京 210016）

随着数字化装配技术的发展，飞机总装引入了部件自动对接技术，该技术依靠数字化测量设备和调姿定位器，能够高效准确地完成飞机部件对接，而且具有一定的柔性，能够适应不同类型的部件对接，大大提高了飞机部件对接质量和效率[1]。其中调姿精度将直接影响最终的装配质量，精确求解部件的目标位姿是调姿的重点环节。

目前，国内的研究主要是对部件的位姿控制点进行测量并依此进行位姿求解[2–4]。由于制造误差和结构变形等因素，造成部件的位姿控制点、对合面与理论模型相比存在较大的偏差，仅采用位姿控制点进行位姿求解会使得部件的对接特征无法准确对接[5]。此外，围框式翼身对接的对合面形状复杂、尺寸大、容差要求严格，如何准确求解围框式翼身对接的目标位姿成为难题。

Devendeville等[6]研究了约束条件下的位姿拟合方法，将部件装配容差约束转化为最优问题进行位姿求解。Beutler等[7]利用解耦闭环极差的方法对机翼位姿进行优化，提高了位姿求解的精度。朱绪胜等[8]提出了基于关键装配特性的最佳装配位姿的多目标优化方法，但是没有考虑对合面的干涉问题。戴肇鹏[9]对围框式平面对接进行了目标位姿计算，没有考虑曲面配合问题。陈磊[10]提出了基于对合面质量的对接协调模型，通过对理论模型对合面协同采样、对测量数据间隙控制点筛选来构建综合协调模型，但是筛选得到的对合面点对距离不能准确代替对合面之间的法向间隙。

实测数据虚拟预装配分析是通过数字化测量设备获取装配件关键特征的实测数据，利用计算机仿真技术进行虚拟装配，然后进行偏差分析和工艺性检查，提前发现装配不协调问题，并对装配准确度进行预评估。张微[11]研究了基于实测数据的飞机装配干涉检测技术，以翼盒为例，对装配对合面的间隙值进行预测。窦亚冬[12]提出了一种基于飞机组件位姿协调的间隙控制方法，分析了扫描测量数据及装配间隙计算结果。基于以上研究基础，本文提出了一种基于实测模型的翼身对接位姿优化方法，通过测量对合面特征并重构，与位姿控制点一起参与飞机翼身对接位姿优化，不仅能准确分析曲面配合间隙，还能在保证机翼位姿在满足其容差要求的前提下确保整个对合面曲面间隙的均匀性，有效解决了仅依据位姿控制点进行位姿求解的弊端，适合多约束下飞机大部件精准对接的装配偏差分析和优化。

1 基于实测模型的位姿优化技术路线

围框式对接是部件间常用的对接形式，例如机翼与机身对接、机翼各段对接等。以ARJ21–700翼身对接为例，机翼和机身的上下左右4个对合面形状复杂，表面是三维自由曲面形式，尺寸大，如图1所示。对接完成后协调对合面之间是嵌合状态，对接时需要保证整个曲面配合间隙的均匀性，容差要求严格。若给定的上反角误差为3′，机翼长10m，则引起对合面间隙的波动量大约有8.722mm。对合面连接质量将直接影响连接部位的安全性和疲劳寿命，进而影响飞机装配质量，本研究在此结构基础上进行。

图1 对合面结构Fig.1 Docking surface structure

在翼身自动对接系统中，涉及到测量辅助装配技术（MAA），该技术首先利用测量系统对部件进行初始位姿标定，然后测量参与对接装配的有关特征的型面轮廓、边缘轮廓等。其次使用“位姿优化”软件计算部件的目标位姿，此过程需要综合分析实测特征、公差约束和理论特征。当位姿优化软件得到部件的目标位姿并进行虚拟装配定位，就可与理论模型进行比较，进行偏差分析，判断是否满足对接装配的所有约束条件。最后驱动自动化设备（如工业机器人、定位器）完成相应的装配对接工作[13]。这种技术的优点在于： （1）大幅度降低工装和夹具的成本； （2）提高装配准确度，从而提高整体产品质量； （3）减少部件装配过程所需的工时等。基于MAA技术基础，本文提出基于实测模型的位姿优化技术路线，如图2所示。具体可以分为以下7个步骤。

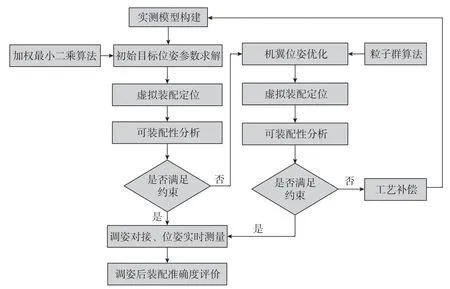
图2 基于实测模型的位姿优化技术路线Fig.2 Technical route of posture optimization based on measured model

步骤1：构建翼身对接实测模型。该实测模型包括机翼位姿控制点和通过测量数据逆向重构而成的机翼、机身之间的对合面。

步骤2：利用加权最小二乘算法对位姿控制点进行拟合得到机翼的初始目标位姿，进行虚拟装配定位。

步骤3：执行可装配性分析，即得到位姿控制点的三维偏差和对合面的间隙、干涉值，如图 3所示。可装配分析过程在试验部分有具体分析过程和结果，在此不再赘述。

图3 可装配性分析Fig.3 Assemblability analysis

步骤4：判断是否满足约束条件。如果满足，则输出目标位姿，进行实际对接装配；若不满足，则执行步骤5。

步骤5：通过分析机翼位姿约束，建立位姿优化模型，采用粒子群算法对目标位姿进行最优化求解，调整机翼的位姿参数，对关键尺寸进行误差分配优化，再次进行虚拟装配定位。

步骤6：执行可装配性分析，即得到位姿控制点的三维偏差和对合面的间隙、干涉值。

步骤7：判断是否满足约束条件。如果满足，则输出最优目标位姿，进行实际对接装配；若不满足，则进行工艺补偿，重新执行步骤1。

2 实测模型构建

2.1 对接装配特征定义

在翼身对接装配过程中，不同的飞机采用不同装配工艺以满足性能要求，本文采用外翼对接法。翼身对接时，中央翼盒已经和机身连接成整体后再与左右外翼进行对接，如图4所示。对接装配特征包括机翼的位姿控制点（姿态特征）和机翼、机身之间的对合面（协调特征）。在测量过程中，通过测量地面上的公共基准点，将测量值由测量坐标系转到飞机装配坐标系下，此坐标转换在测量过程中通过使用测量软件自动完成。因此本文中的坐标系有且只有飞机装配坐标系，测量数据都是飞机装配坐标系{g}下的测量值。

图4 翼身对接装配特征Fig.4 Wing-body docking assembly features

2.2 翼身对接实测模型构建

翼身对接实测模型构建是基于围框式翼身对接装配特征定义进行的。首先需要对位姿控制点和对合面进行测量，然后将激光扫描仪T–Scan釆集到的对合面扫描点云数据进行预处理，包括噪声点去除、数据修补、数据精简、三角网格化等[14]，最后对机翼、机身对合面三角化数据进行逆向重构[15]，在重构的机翼对合面上均匀生成对合面控制点。

通过上述步骤，在结构树上生成若干对合面重构特征、对合面控制点等几何图形集。本文将以上生成的若干几何图形集，还包括位姿控制点测量值几何图形的总和定义为翼身对接实测模型，如图5所示。

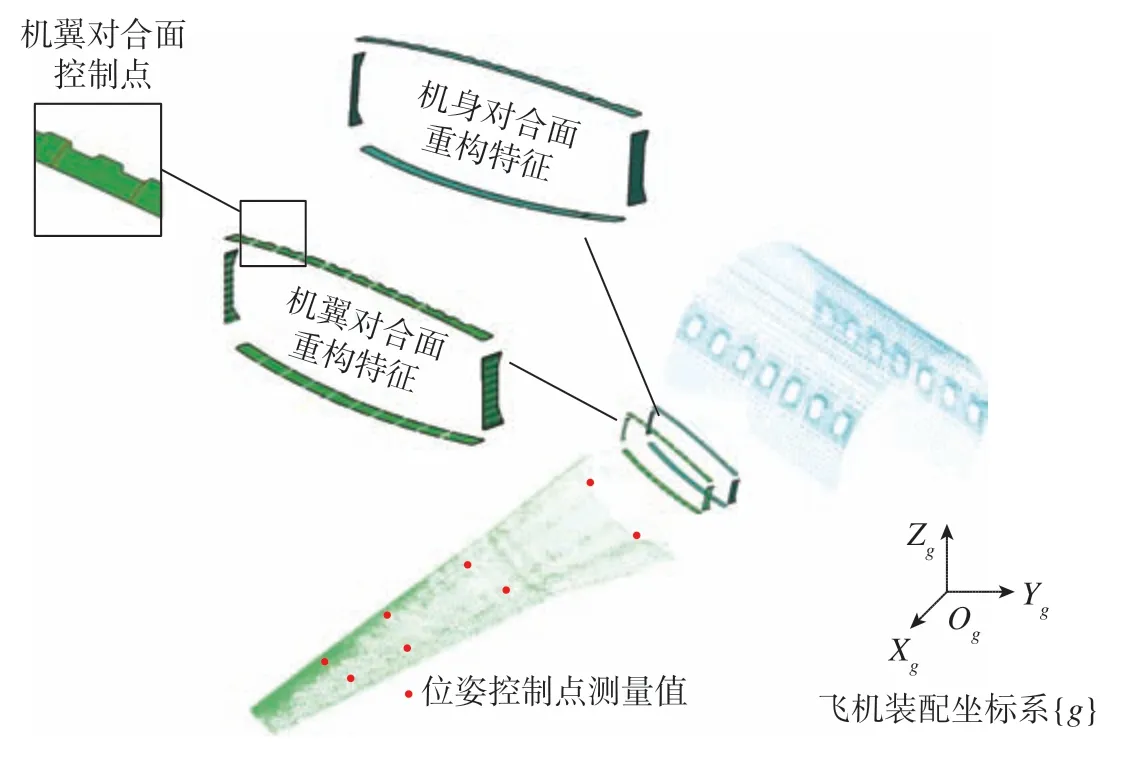
图5 翼身对接实测模型Fig.5 Wing-body docking measured model

3 机翼位姿优化

在机翼制造过程中，由于零件制造误差、定位误差、结构受重力和应力变形等因素的影响，机翼在飞机装配坐标系下的理论位姿不能作为实际对接的目标位姿[16]。下文通过分析机翼位姿约束来建立机翼位姿优化模型，得到机翼的最优目标位姿。

3.1 机翼位姿约束

3.1.1 位姿控制点容差

对实测模型进行定位后，需要对位姿控制点进行偏差分析，保证定位后的位姿控制点在容差范围内，如图6所示。

调姿后第i个位姿控制点在飞机装配坐标系{g}的残差为

n个位姿控制点的误差为

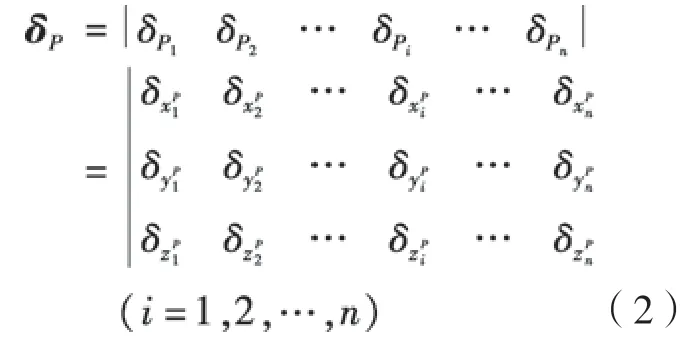
对于单个位姿控制点，在某方向上容差要求是对称的，即±tol，则容差要求矩阵为

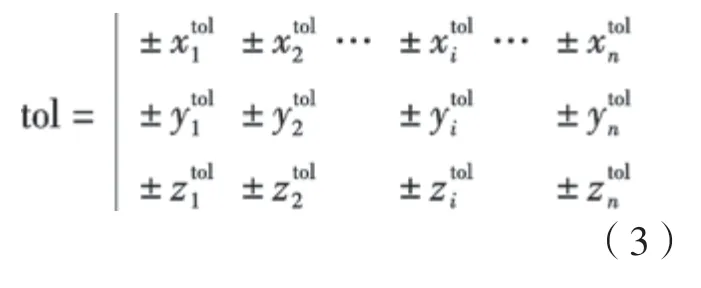
超差矩阵OverTol记为

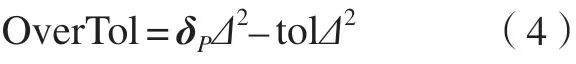
式中，Δ2表示矩阵元素的平方。

约束：位姿控制点在容差范围内。

3.1.2 对合面间隙容差

对实测模型进行定位后，需要进行对合面间隙分析，要保证对合面不产生干涉，间隙分布均匀，满足间隙容差要求。机身对合面控制点由机翼对合面控制点投影得到，形成一一对应的对合面控制点对，此点对距离能准确代替对合面之间的法向间隙，并将对合面间隙约束转化为对合面控制点组特征约束，如图 7所示。

图7 对合面控制点组特征约束Fig.7 Feature constraint of mating surface control point group

调姿后第j个对合面控制点处在{g}中的间隙为

第k（k=1，…，4）个对合面的mk个对合面控制点处的间隙为

（1）约束1：对于每个对合面控制点处的间隙，要求不能干涉，即

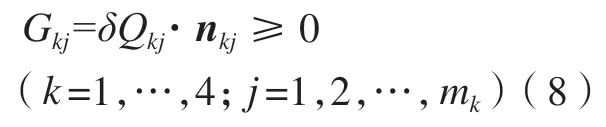
式中，nkj为机身第k（k=1，…，4）个对合面上第j个控制点处的单位法向量，方向为机翼理论模型上的控制点指向机身理论模型上的控制点。

mk个控制点的要求为

（2）约束2：对合面之间的距离（各处的法向间隙）的最大值与最小值可作为对合面控制点对配准的限定条件，以保证间隙均匀，实际点对之间的距离必须在确定的最大间隙dmax和最小间隙dmin之间。由于制造误差存在，对间隙限定条件进行适当放宽，即d′max=dmax+δ，d′min=dmin–δ，由此确定约束函数为

3.2 机翼位姿优化模型建立

点组特征与对合面特征的协同优化问题可以转换为带约束的最小化问题求解。最小化目标函数为对合面的间隙总和，即矩阵δQ的各元素平方和；约束为每个位姿控制点3个方向均在容差范围内；对合面不会发生干涉；第k个对合面间隙要均匀，在规定的间隙容差范围内。因此，采用加权最小二乘目标函数，即

最终，构建统一约束模型，即目标位姿变换参数计算模型为

3.3 机翼位姿优化模型求解

粒子群优化算法（Particle swarm optimization，PSO）是个体协作而成的群体与个体间的互动机制中寻求搜索全局最优解的方法，具有实现简单、解算效率高、非线性优化性能强等优点[17]。本文采用粒子群算法对位姿参数进行最优化求解。

将目标位姿参数作为由N个粒子组成的一个粒子群中一个优化粒子，维度D=6，则第i个粒子表示为一个6维的向量Zi=[ΔXiΔYiΔZiεxiεyiεzi]T（i=1，2，…，N）。设第i个粒子的最优位姿是Pi，整个群体经过的最优位置是G，第i个粒子的速度和位置更新公式为

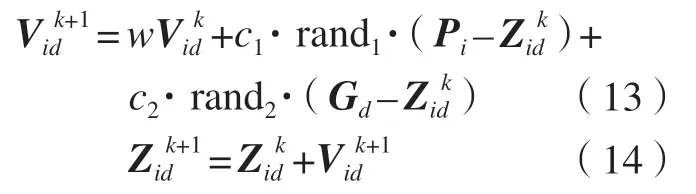
式中，w为惯性权重；c1、c2为学习因子；rand1、rand2为0～1之间的随机数；d表示第几维元素。这里取w=0.9，c1=1.5，c2=2.5，N=30，迭代次数Maxiter=15。由第i个粒子构造的适应度函数：

式中，minF（Zi）、s.t.参照前文为罚因子。算法流程如图 8所示。

图8 算法流程图Fig.8 Algorithm flowchart

4 试验验证与分析

4.1 试验平台建立

本文以围框式翼身模拟件对接为例（图9），验证算法的有效性。测量设备选用Leica激光跟踪仪和激光扫描仪T–Scan。机翼、机身采用自主研制的柔性定位器支撑和调姿，先进行机身调姿，然后锁紧固定，最后进行机翼调姿。由于测量设备、调姿机构等可能存在误差，调姿为多次逼近过程，需要进行多次位姿测量、解算和调整操作，直到位姿符合对接精度和质量要求。

图9 翼身模拟件对接应用试验Fig.9 Wing-body analog docking application test

4.2 实测模型构建

布设好测量场后，采用Leica激光跟踪仪测量机翼位姿控制点得到数据信息如表1所示，采用激光扫描仪T–Scan测量机翼、机身对合面，利用前文方法对合面进行重构，如图10所示。

图10 特征重构Fig.10 Feature reconstruction

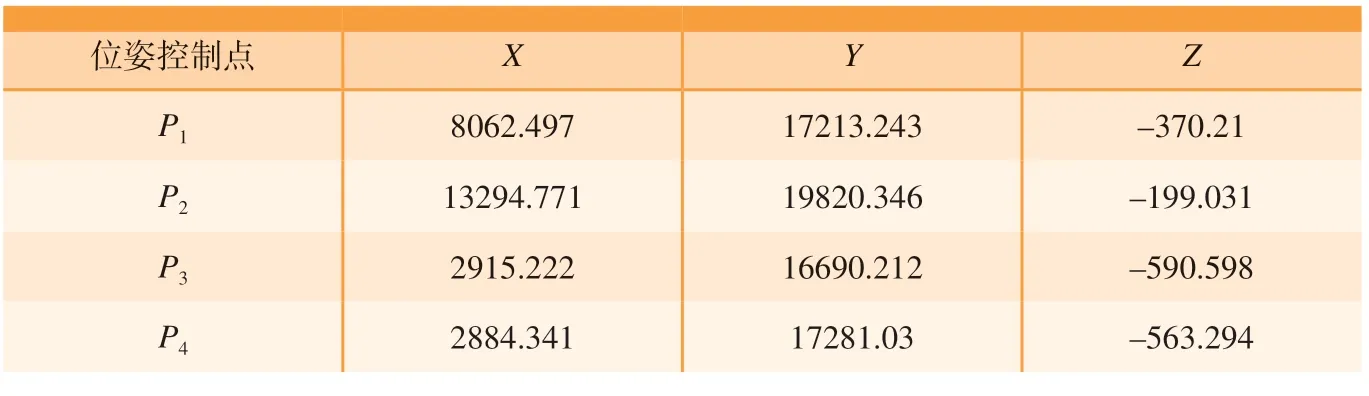
表1 机翼位姿控制点测量值Table 1 Wing posture control points measurement values mm

为了提高效率，利用开发的软件生成对合面控制点[18–19]。具体如下：以机翼对合面重构特征为对象，按照10mm×10mm的网格密度分别在机翼右、左、上、下对合面上生成控制点。此处采用U–V参数离散法即映射离散法，即将曲面展成为一张平面，在平面上进行布点后映射回原始曲面上，离散速度快[20]。该过程需手动选取待离散曲面并输入U、V方向的离散点数量或者长度，点击确认实现自动化离散，如图11所示。

图11 机翼对合面控制点生成Fig.11 Control point generation of wing mating surface

4.3 位姿约束

机翼位姿控制点理论坐标和容差要求如表2所示，对合面之间距离（各处的法向间隙）的限定条件如表3所示。

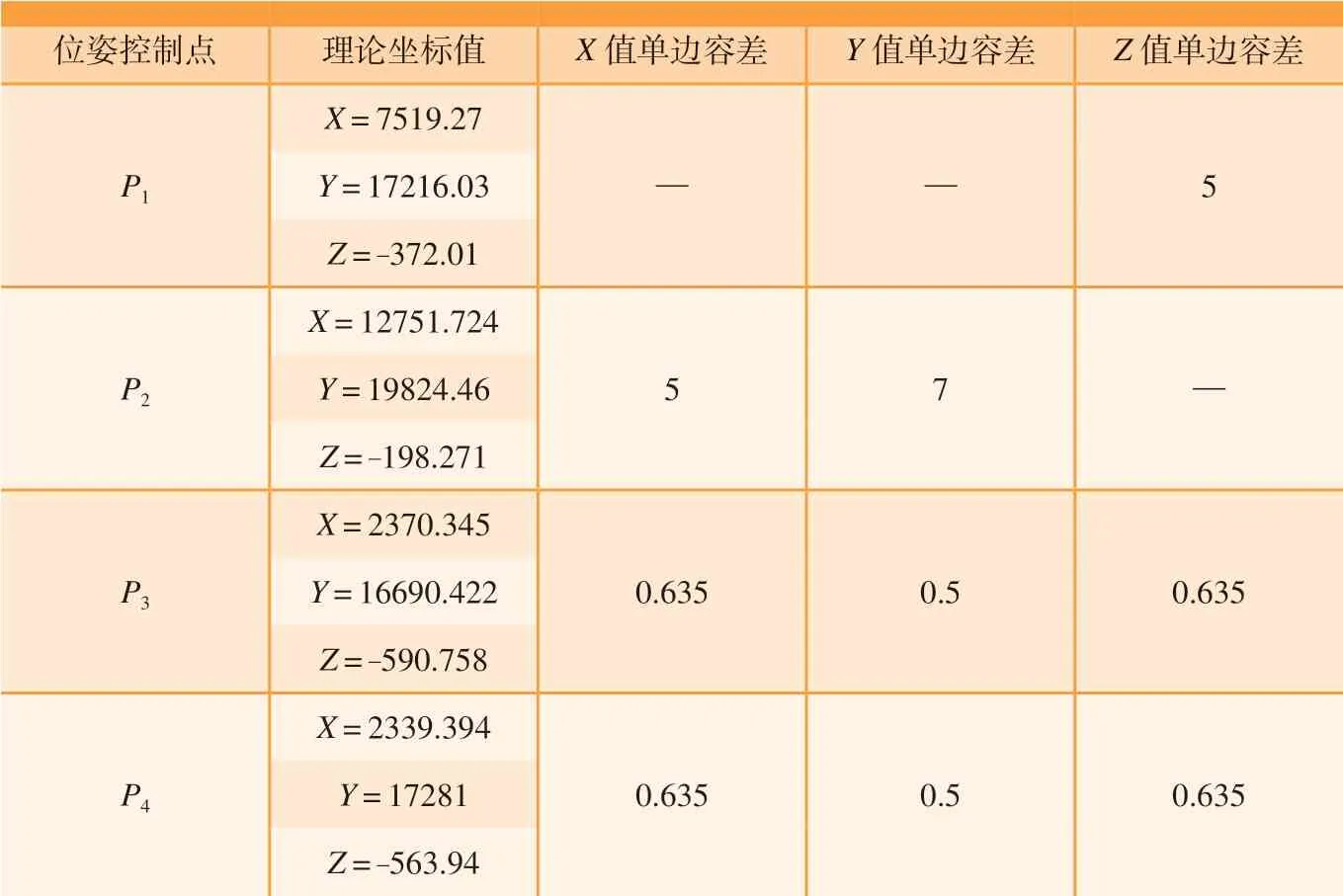
表2 机翼位姿控制点理论坐标和容差要求Table 2 Theoretical coordinates and tolerance requirements of posture control points mm

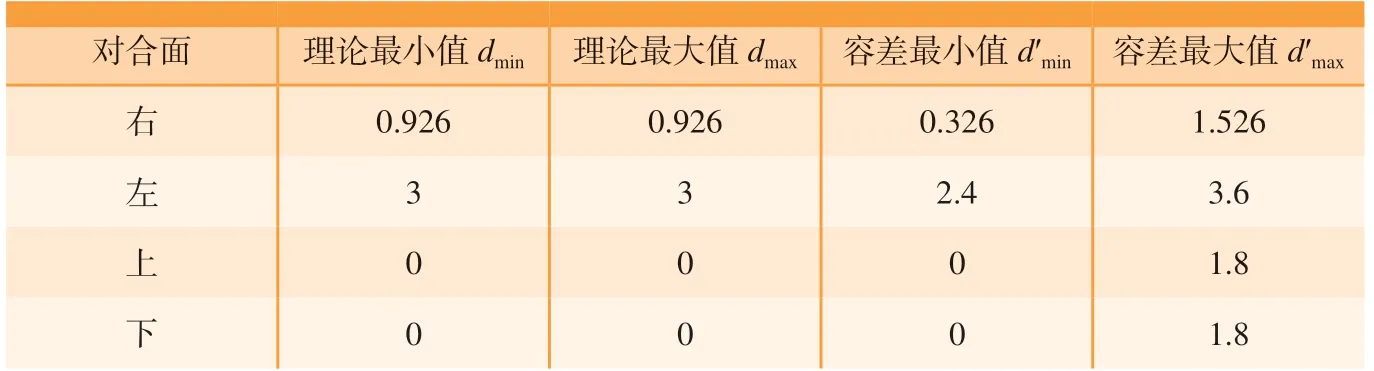
表3 对合面距离限定条件Table 3 Limiting condition of mating surface distance mm

4.4 位姿优化

首先利用加权最小二乘算法（权重与容差带宽成反比）得到机翼初始目标位姿，如表 4的第2列所示，将构建的机翼实测模型（包括机翼的位姿控制点、对合面、对合面控制点）按照此初始目标位姿进行平移和旋转；然后将机翼对合面控制点投影到机身对合面上，得到对应机身对合面控制点；最后利用粒子群算法对对合面间隙优化模型进行求解，得到最终目标位姿，如表4所示。

表4 目标位姿计算结果Table 4 Target posture calculation result

对实测模型进行可装配性分析的结果如表5和图12所示。从表5可以看出，仅采用加权最小二乘算法对位姿控制点进行拟合，并按照此初始位姿进行调姿，位姿控制点P1、P2、P3和P4的拟合残差均在表2规定的容差范围内，满足翼身对接装配对位姿控制点的要求。其中P1、P2的拟合残差较大，P2的z方向残差达到了4.908mm，这是由于点P1、P2远离翼根处，其误差对装配准确度影响较小，因此表2中对该两点的约束较为宽松。从图12可以看出，右侧间隙值偏差最大有0.938mm，超过表3规定的容差半带宽0.6mm有0.338mm。同理可知左对合面也出现了间隙超差现象，上对合面甚至出现了0.195mm的干涉，这严重降低了翼身对接质量。

表5 位姿控制点拟合残差Table 5 Posture control point fitting residuals mm

而采用本文的优化方法，可以有效解决点组特征和对合面特征组成的协同优化问题，从表5可以看出，位姿控制点P1、P2、P3和P4的最终拟合残差相对初始残差略有变化，但均在表2规定的容差范围内，满足翼身对接装配对位姿控制点的要求。从图 12可以看出，右、左、上、下对合面的间隙值均在表3规定的容差范围内。右对合面平均间隙偏差从0.781mm降为0.418mm，左对合面平均间隙偏差从0.825mm降为0.465mm。上对合面平均间隙偏差从0.629mm升为0.876mm，下对合面平均间隙偏差从0.573mm升为0.816mm（上、下对合面平均间隙偏差上升是为了消除上对合面0.195mm的干涉，机翼的位姿向z轴的正方向微调）。左、右对合面间隙实现了表3中规定1.2mm的容差带宽约束，上下对合面间隙实现表 3中规定1.8mm的容差带宽约束。这表明采用本文的优化方法可以准确获取机翼的位姿调整参数，对关键尺寸进行误差分配优化，同时保证了翼身间的相对位置准确度和对合面之间的协调准确度。

图12 间隙值优化结果Fig.12 Gap value optimization result

按照最优目标位姿对机翼进行实际的调姿对接，如图13所示，试验结果表明对合面间隙分布均匀，对合面质量符合要求。

图13 翼身对接完成Fig.13 Wing-body docking completed

最后选取对合面间隙测量位置，对比实际装配后的测量结果与可装配性分析结果，验证可装配分析方法的准确性。此次试验定义了机翼与机身的上对合面中的5个位置，如图14所示。在实测模型中的5个对应位置提取间隙值，如表6中的第2列所示。在对接装配完成后使用塞尺对图14所示位置的间隙进行测量，并记录下测量值，如表6中的第3列所示。从表6中的对比数据可以看出，可装配性间隙分析结果与装配后间隙实测结果的最大差值为0.08mm，满足可装配分析精度±0.1mm的要求。

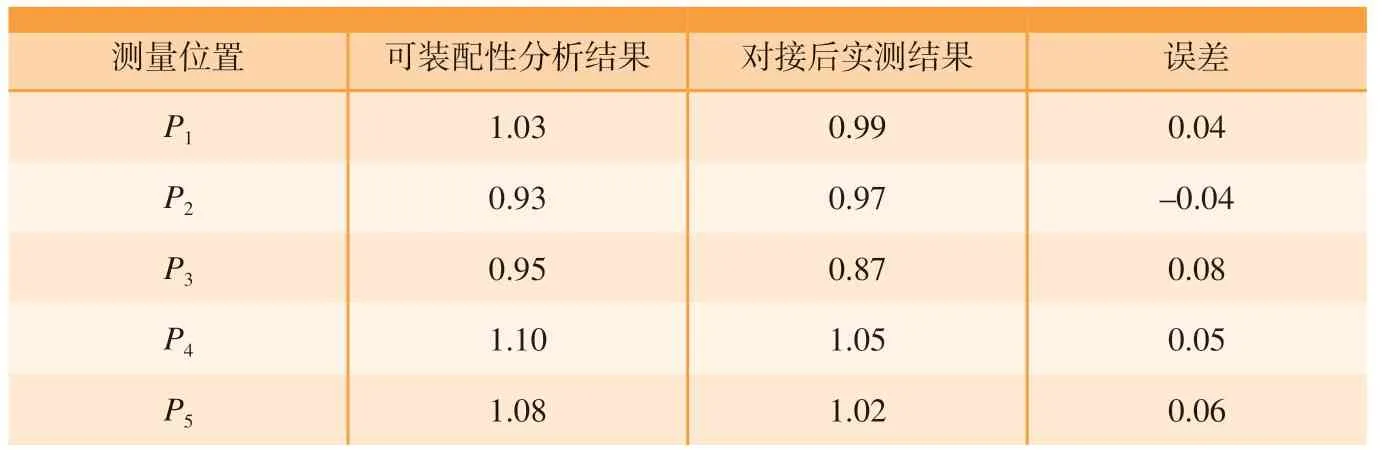
表6 可装配性分析结果与实测结果Table 6 Assemblability analysis results and measured results mm

图14 间隙测量位置Fig.14 Gap measurement position

5 结论

（1）仅以位姿控制点作为对接基准，采用加权最小二乘算法对位姿控制点进行拟合，位姿控制点在容差范围，但是会造成对合面间隙超差，严重降低翼身对接质量。

（2）本文提出的位姿优化方法，能够保证机翼位姿控制点在容差范围内，左右对合面间隙实现1.2mm的容差带宽约束，上下对合面间隙实现1.8mm的容差带宽约束。说明本文提出的位姿优化方法可行，能够有效解决协同优化问题，提高翼身对接质量。

（3）可装配性间隙分析结果与装配后间隙实测结果的最大差值为0.08mm，满足可装配分析精度±0.1mm的要求。

（4）本文研究为围框式翼身对接装配质量的控制提供新的方法和思路。此外，本文的方法不仅可用于围框式翼身对接，对于由点组特征和对合面特征组成的协同优化问题也适用。