毛毛虫树的L(3,2,1)-标号问题
张小玲
(集美大学师范学院,福建 厦门 361021)
图的距离标号问题源于无线电网络中的频率分配问题,即给每个无线电发射台分配一个频率,使得相互干扰的无线电发射台所分配的频率间隔落在允许的范围之内.关于频率分配问题的研究已有数十年的历史,1980年,Hale[1]将此问题归结成图的T-着色问题.1992年,Griggs等[2]将该问题抽象为图的距离标号问题,并考虑了更一般的L(p,q)-标号问题.从此,图的L(p,q)-标号问题得到了广泛研究,详见文献[3-4].
2004年,学者们开始研究图的L(3,2,1)-标号问题.Griggs等[2]已经证明了确定一般图G的L(3,2,1)标号数是NP-困难的问题.因而,确定一些特殊图类的L(3,2,1)标号数或给出L(3,2,1)标号数的上下界成为极具意义的研究课题.如,Shao[5]研究了Kneser图,Halin图等的L(3,2,1)-标号,并给出这些图类的L(3,2,1)标号数的上下界.Chia等[6]考虑了一般图和树的L(3,2,1)标号数的上下界.Clipperton[7]确定了路、圈、n-元树、完全图和完全二部图的L(3,2,1)标号数.同时也证明了对任意毛毛虫树T,有2Δ+1≤λ3,2,1(T)≤2Δ+2.我们在已有研究的基础上,对毛毛虫树的L(3,2,1)-标号进行研究,纠正了Clipperton等[7]的一个错误,并完全确定了最大度不小于4的毛毛虫树的L(3,2,1)标号数.
1 预备知识
对于任意非负整数i,j(i 定义1图G的L(3,2,1)-标号是指从顶点集V(G)到非负整数集Z*的一个映射f,满足:对于任意两个不同顶点u和v,若d(u,v)=i(i=1,2,3),则|f(u)-f(v)|≥4-i.若图G的一个L(3,2,1)-标号中的所有像元素都不超过整数k,则称之为图G的k-L(3,2,1)-标号.图G的L(3,2,1)标号数,记作λ3,2,1(G),是使得图G存在k-L(3,2,1)-标号的最小整数k. 引理1[6]若f是G的一个k-L(3,2,1)-标号,则映射f′:V(G)→[0,k]也是G的k-L(3,2,1)-标号,其中f′(v)=k-f(v). 引理2[6]设T是一棵树,则2Δ+1≤λ3,2,1(T)≤2Δ+3.进一步地,若λ3,2,1(T)=2Δ+1且f是T的一个(2Δ+1)-L(3,2,1)-标号,则对于T的每个Δ-点v,均有f(v)∈ {0,2Δ+1}. 注1根据引理2,若λ3,2,1(T)=2Δ+1且f是T的一个(2Δ+1)-L(3,2,1)-标号,则对于每个Δ-点v,都有f(v)∈{0,2Δ+1}.并且当f(v)=0时,有f(N(v))=O[3,2Δ+1];当f(v)=2Δ+1时,有f(N(v))=E[0,2Δ-2]. 根据引理2和注1,不难得到如下定理. 定理1设T是一棵树.若T满足条件(i)或(ii),则λ3,2,1(T)≥2Δ+2. (i)T中存在两个Δ-点v1,v2,使得d(v1,v2)=2; (ii)T中存在三个Δ-点v1,v2,v3,使得对于1≤i,j≤3,都有d(vi,vj)≤3. 毛毛虫树是指去掉悬挂点和与其关联的悬挂边后只剩下一条路(记为P=v1v2…vn)的树,其中P称为毛毛虫树的脊椎,vi称为毛毛虫树的脊椎点.设T是毛毛虫树,若Δ≤2,则T是一条路.下文将证明对于最大度不小于4的毛毛虫树T,条件(i)是λ3,2,1(T)=2Δ+2的充要条件. Clipperton等[7]研究了毛毛虫树的L(3,2,1)-标号,并给出如下结果. 定理2[7]设Pn是一条具有n个顶点的路,则 定理3[7]设T是毛毛虫树且Δ≥3,则2Δ+1≤λ3,2,1(T)≤2Δ+2.若T中任意4个连续的脊椎点至多包含两个Δ-点,则λ3,2,1(T)=2Δ+1. 注2定理3的后半部分是错误的.事实上,如果T只包含两个距离为2的Δ-点,显然满足T中任意4个连续的脊椎点至多包含两个Δ-点,但由定理1可得λ3,2,1(T)≥2Δ+2. 定理4设T是毛毛虫树且Δ≥4.那么λ3,2,1(T)=2Δ+1当且仅当T中不存在两个距离为2的Δ-点. 证明必要性.反证,若T包含两个距离为2的Δ-点,则根据定理1,有λ3,2,1(T)≥2Δ+2.结合定理3,可知λ3,2,1(T)=2Δ+2,但这与假设相矛盾. 充分性.设v1v2…vn是T的脊椎,vi1,vi2,…,vik是T的所有Δ-点,其中i1 首先,用0,2Δ-1,2,2Δ+1的模式循环标记vi1vi1-1…v1.一般地,假设vij-1…vij已经标记,其中2≤j≤k.下面分5种情形标记vij…vij+1. 情形1d(vij,vij+1)=1. 若(f(vij-1),f(vij))=(5,0)或(2Δ-1,0),则vijvij+1标记X1=0(2Δ+1). 情形2d(vij,vij+1)=4t+3,其中t≥0. 若(f(vij-1),f(vij))=(5,0),则vij…vij+1标记X2. 若(f(vij-1),f(vij))=(2Δ-1,0)或(2Δ+1,0),则vij…vij+1标记X′2. 其中 情形3d(vij,vij+1)=4t+4,其中t≥0. 若(f(vij-1),f(vij))=(5,0)或(2Δ-1,0)或(2Δ+1,0),则vij…vij+1标记X3. 其中 情形4d(vij,vij+1)=4t+5,其中t≥0. 若(f(vij-1),f(vij))=(5,0)或(2Δ-1,0)或(2Δ+1,0),则vij…vij+1标记X4. 其中 情形5d(vij,vij+1)=4t+6,其中t≥0. 若(f(vij-1),f(vij))=(5,0)或(2Δ-1,0)或(2Δ+1,0),则vij…vij+1标记X5. 其中 接下来,若f(vik)=0,则用0,3,6,9的循环模式标记vikvik+1…vn;对称地,若f(vik)=2Δ+1,则用2Δ+1,2Δ-2,3,0的循环模式标记vikvik+1…vn. 最后,若f(vi)为奇数,则用E[0,2Δ]{f(vi)±1,f(vi-1),f(vi+1)}标记vi的叶子邻点;若f(vi)为偶数,则用O[1,2Δ+1]{f(vi)±1,f(vi-1),f(vi+1)}标记vi的叶子邻点. 不难证明,上述每种情形下的片段均是可行的(2Δ+1)-L(3,2,1)-标号且每种情形下的标号都可相互衔接.因而,f是T的一个(2Δ+1)-L(3,2,1)-标号.故λ3,2,1(T)=2Δ+1. Clipperton[7]证明了对任意的最大度不小于3的毛毛虫树T,都有2Δ+1≤λ3,2,1(T)≤2Δ+2.且当T中任意4个连续的脊椎点至多包含两个Δ-点时,有λ3,2,1(T)=2Δ+1.我们发现这个结果的后半部分是错误的.本文纠正了这一错误,并完全确定了最大度不小于4的毛毛虫树的L(3,2,1)标号数.2 主要结果
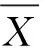
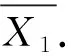

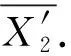

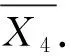

3 结 论

