基于数据非线性预处理的结构动力响应贝叶斯回归代理模型

林智炜，付赛赛，陈 俊，王东东

(厦门大学建筑与土木工程学院，福建省滨海土木工程数字仿真重点实验室，福建 厦门 361005)

结构动力分析通过计算结构在不同荷载条件下位移、应力等时变信息来评估结构的安全性，是有限元分析领域的一个重要研究内容[1].在结构动力有限元分析中，通常在空间进行有限元离散，而在时间域上采用差分法进行离散，常用的方法有Newmark-β法、Wilson-θ法、HHT(Hilbert-Hughes-Taylor)法等[1].然而，随着结构形式日益大型复杂化，在细化空间离散的同时也减小了时间离散步长，使得有限元动力分析计算量陡增，难以同时保证效率与精度.为了提高计算精度和效率，许多学者对时间积分算法进行了改进.例如，李志彬等[2]改进Generalized-α法并提高了结构大变形动力学问题的求解精度，Noh等[3]通过调节时间步长的比率提升了隐式直接时间积分方法的精度.但是，这些算法方面的改进仍然很难满足实际工程结构的动力分析效率需求，在进行复杂结构动力分析时耗时长、效率低的困难更加凸显.因而，如何在保证精度的前提下提高计算效率是结构动力分析中的一个核心问题.

近年来，人工智能技术的快速发展为提升结构分析的效率和鲁棒性提供了契机[4-5].例如，Afshari等[6]将机器学习技术与结构可靠度相结合；Feng等[7]利用能量守恒神经网络进行结构在地震作用下的动力学分析；陈健等[8]发展了与无网格法相匹配的循环卷积神经网络结构设计方法和动力分析的代理模型.同时，由于数据维数伴随着样本往往呈指数增长，机器学习的数据呈现超高维数趋势，数据选择与处理已然成为重点问题[9]，例如Xie等[10]通过检测特定类别的重要协变量进行高维异构数据的类别自适应筛选.本文基于贝叶斯回归算法[11]，研究基于数据预处理的有限元动力分析的机器学习代理模型，以加速结构动力响应分析的计算过程.

贝叶斯回归(Bayesian regression)是一类基于贝叶斯推断的回归模型[11].在贝叶斯回归中，将输入参数作为随机变量参与计算，然后通过已知的先验信息和模型似然分析其后验概率分布.贝叶斯回归对数据有较强的自适应能力，可有效防止过拟合现象，具有比较广泛的适用性，但初始数据对模型的预测精度仍有明显影响.Sigmoid激活函数具有高阶光滑的特点，可将变量输出至区间(0,1)[12]，相对原始数据增加了非线性关系，从而使贝叶斯回归模型与结构动力分析之间的结合更加准确.B样条基函数是一组高阶连续的分段多项式，其函数阶次p与数量nB可以同时灵活地进行调整[13].基于B样条基函数的处理步骤灵活地增加了输入数据的维度，可以提高贝叶斯回归模型的预测精度.

本文以结构时域内不同时刻动力响应之间的概率关系为研究对象，基于有限元节点形函数的影响域范围对输入数据进行相应提炼和压缩，形成数据训练集；随后通过激活函数和B样条基函数对数据进行非线性预处理，突出结构关键节点的预测精度，进而提出了一种结构动力分析的贝叶斯回归代理模型.该代理模型在保证结构计算精度的同时，显著提高了结构动力分析的计算效率.

1 贝叶斯回归模型的基本理论

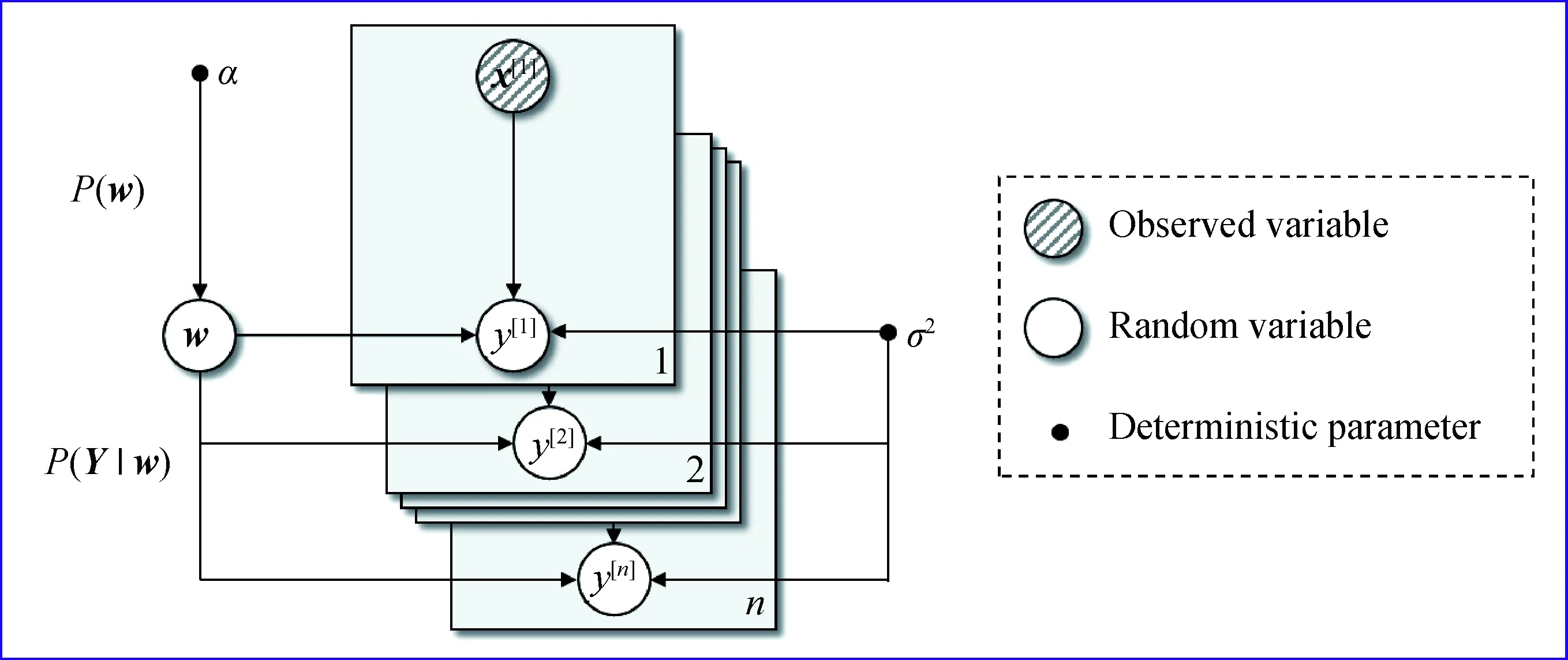
图1 贝叶斯回归概率图模型示意图Fig.1 Illustration of Bayesian regression probabilistic graphical model

y[i]=wTx[i]+ε,

(1)

其中ε为偏差，假定其服从高斯分布G(ε|0,β-1)，β为方差参数.w=[w1,w2,…,wm]T为待定模型参数.为方便表述，将n组自变量的集合表示为X=[x[1],x[2],…,x[n]]，n组因变量表示为Y=[y[1],y[2],…,y[n]]T.由此，模型的似然函数可表示为如下形式：

(2)

其中似然函数P(Y|w)表示给定参数w后变量Y的发生概率.

假定模型参数w同样服从高斯分布，其先验分布可表示为：

P(w)=G(w|0,α-1I),

(3)

其中向量0、I维度与参数w相同.因而，模型的联合概率分布P(Y,w)可以由式(2)和(3)得到：

P(Y,w)=P(Y|w)P(w).

(4)

此外，根据条件概率公式[12]，该模型的后验分布为：

(5)

其中mN=β(αI+βXXT)-1XY为概率分布的均值，SN=(αI+βXXT)-1为概率分布的方差.值得指出的是，当得到模型参数的概率分布后，还需求解模型参数w用于模型的预测计算.

2 训练集数据预处理

2.1 有限元动力分析数据

(6)

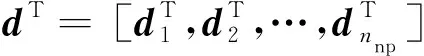
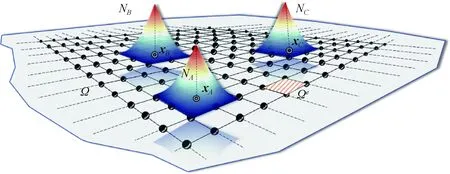
图2 有限元离散及节点形函数示意图Fig.2 Illustration of finite element discretization and nodal shape functions

基于式(6)的位移近似，不考虑阻尼影响的结构有限元动力离散方程可以表示为：

(7)

其中：f为力向量；M和K为质量和刚度矩阵，表示为

(8)

式中：ρ为密度，N为单元形函数矩阵，D为弹性矩阵，B为位移梯度矩阵，A表示将单元矩阵组装为整体矩阵的算子[1].利用有限元形函数的单元局部近似特性，质量和刚度矩阵均可通过单元计算和整体组装的有限元标准分析流程得到[1].

式(7)仅包含有限元空间离散，要进行时程分析需要在时间上引入离散，这里采用具有二阶精度的中心差分法.在式(7)引入中心差分法和集中质量矩阵后，可得如下的时空全离散的运动方程：

d[i+1]=Δt2M-1(f[i]-Kd[i])+2d[i]-d[i-1],

(9)

其中Δt=ti+1-ti.当ti-1和ti时刻的位移d[i-1]和d[i]及力向量f[i]已知时，可根据式(9)计算ti+1的位移，以此类推可获得全时程上的动力响应.但是由于在结构动力计算时每个节点产生一组乃至多组响应数据，若直接将所有节点的动力响应作为模型输入进行训练及预测计算，显然将导致计算时间大幅增加，因此这里根据所关注的关键位置及节点形函数的影响域选择周围相关节点的动力响应数据构建数据训练集.

2.2 数据非线性预处理

结构在受到荷载作用产生动力反应时，相邻时刻之间的动力响应往往由于荷载在空间和时域上的复杂性而相应呈现出复杂的非线性关系.为使贝叶斯回归模型与结构动力分析能更加准确结合，需要对输入模型的结构响应与激励的训练集数据进行非线性处理.

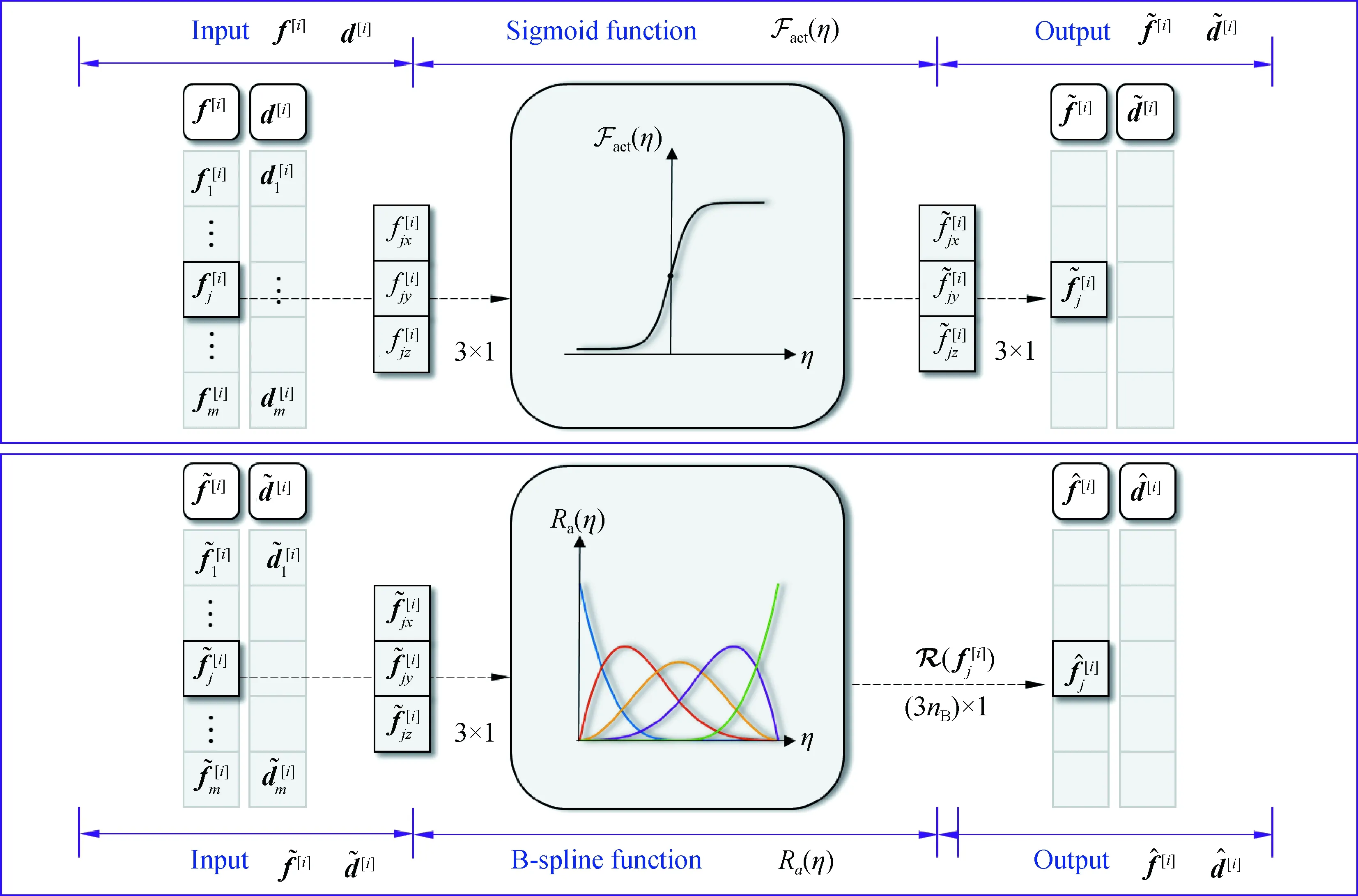
图3 数据非线性预处理流程Fig.3 Flowchart for nonlinear data preprocessing operations

Sigmoid激活函数将输入数据转化为区间(0,1)之间的输出数据，其表达式为：

Fact(η)=(1+e-η)-1.

(10)

对于一组向量变量η=[η1,η2,…,ηm]T，为方便表述，将Fact(η)定义为：

Fact(η)=[(1+e-η1)-1,(1+e-η2)-1,…,(1+

e-ηm)]T.

(11)

经过该数据处理，有限元节点力向量f[i]和位移向量d[i]变为：

(12)

(13)

和

(14)

为清晰起见，后续讨论中采用Ra来表示Rap，省略基函数的阶次.

对于一组向量变量η=[η1,η2,…,ηm]T，引入如下的扩展数据变量R(η)：

R(η)=[R1(η1),…,RnB(η1),R1(η2),…,

RnB(η2),…,R1(ηm),…,RnB(ηm)]T,

(15)

(16)

(17)

由上述数据非线性预处理过程可以看出，本文所提的非线性处理步骤在一定程度上保留了原始数据的特征，但通过引入B样条基函数对数据进行了扩展，丰富了数据信息.后续结构动力响应贝叶斯回归模型中的数据训练与预测均采用这些经过基函数扩展的非线性化结构动力分析数据.

3 结构动力响应分析的贝叶斯回归模型

基于贝叶斯回归的结构响应代理模型同样采用逐步求解方法，假定结构第i时刻的动力响应与该时刻之前的动力响应及外界激励相关，同时认为关联性的强弱与时刻的远近有关.现对一个有限元结构选取m个节点进行分析，其节点自由度为md.连续的3个i-1、i与i+1时刻之间位移响应可表示为以下形式：

(18)

W=[w1,w2,…,wmd],

(19)

其中wj为一组3md×(2+nB)维的列向量，体现了第j个节点的位移响应与输入变量之间的相关性.

(20)

根据模型似然与参数后验分布可以对第k时刻结构位移响应进行预测，表示为：

(21)

图4为基于贝叶斯回归的结构响应代理模型的计算框架和模块，基于该模型可逐步预测每时刻所选择的结构节点位移，最终得到结构动力响应的代理模型预测解.

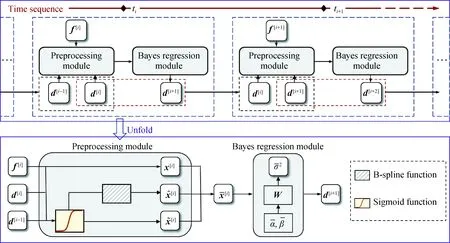
图4 结构动力响应的贝叶斯回归代理模型的计算框架与模块Fig.4 Computational framework and module of the Bayesian regression surrogate model for structural dynamic response

4 数值算例

4.1 一维弹性杆问题

图5 一维弹性杆问题Fig.5 1D elastic rod problem

对于该问题，计算总时长T=2 s，时程分析时间步长为Δt=0.001 s，总时间步数为2 000，选用中心差分法计算有限元模型动力响应，并选取前200步有限元数据作为训练集数据进行贝叶斯回归代理模型训练，后续1 800步作为目标解与模型预测解进行对比的数据.数据预处理参数p=3，nB=5.图6给出代理模型选取节点数m=11时的数据传递过程.值得注意的是，对于一维问题，节点数与自由度数相等，即m=md.

图6 基于数据非线性预处理的结构动力响应贝叶斯回归代理模型的详细数据传递过程Fig.6 Detailed data transfer procedure of the Bayesian regression surrogate model for structural dynamic response with nonlinear data preprocessing

图7为弹性杆在体力f(x,t)=1 000sint/(t+1)N作用下于x=L/2处的时域位移响应结果，m=11表示结构全部节点同时参与模型训练与位移响应预测，m=6表示代理模型仅选择位于区间(0,L/2)的节点进行训练与结果预测.贝叶斯代理模型的训练集分别采用经过预处理的数据与未处理的原始数据进行训练，并将有限元直接分析结果作为参照解来对比其预测结果.图8为其在f(x,t)=1 000sin(x+t)N作用下的动力响应.结果表明，基于数据非线性预处理的贝叶斯代理模型的结构响应预测结果与有限元动力分析参照解结果吻合良好.另一方面，训练数据的完整性对仅使用原始数据直接训练的贝叶斯代理模型预测精度有明显影响，而数据的非线性预处理可以有效提升训练数据不完整情况下的预测结果.同时由不同数据训练构造的代理模型均较好地给出动力响应的预测值，体现出所提的代理模型对荷载类型的泛用性.

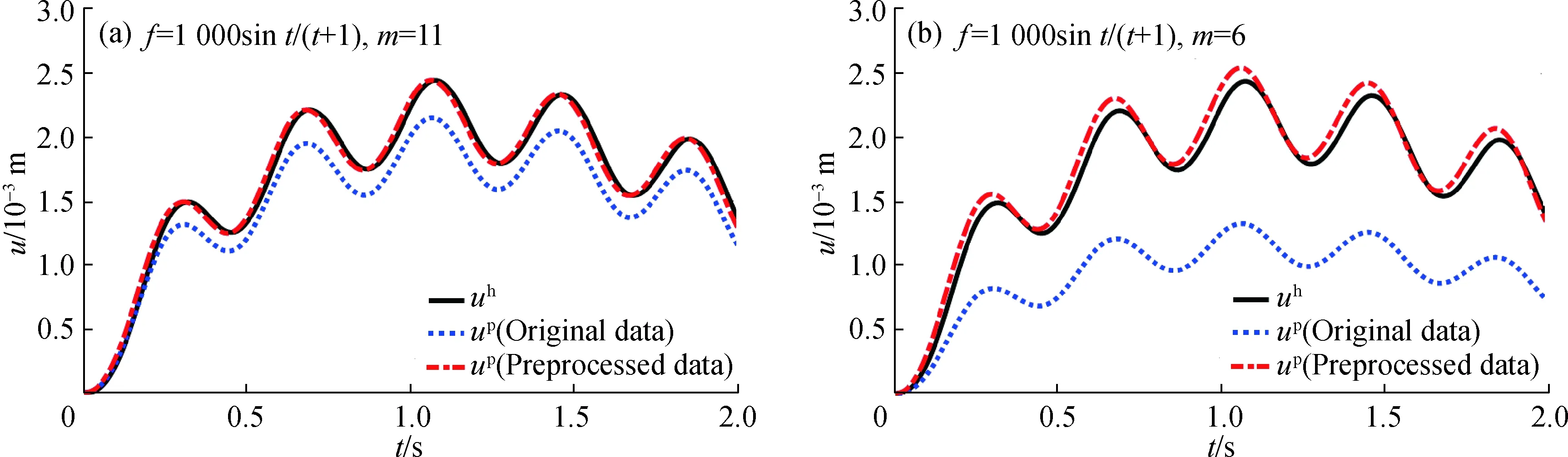
图7 有无数据预处理的代理模型对f=1 000sin(t)/(t+1)的预测结果对比Fig.7 Comparison of predicted results by the surrogate model with and without data preprocessing under f=1 000sin(t)/(t+1)

图8 贝叶斯回归代理模型对f=1 000sin(x+t)的预测结果对比Fig.8 Comparison of predicted results by the Bayesian regression surrogate model under f=1 000sin(x+t)

4.2 三维框架问题

第2个算例是图9所示的三维四层混凝土框架结构动力分析问题.对于该问题，采用三维四面体单元进行精细离散分析，包括111 127个单元，227 590个节点.该结构的材料常数为：密度ρ=2 300 kg/m3，弹性模量E=30 GPa，泊松比ν=0.18.框架尺寸为：L1=6 m，L2=3 m.该结构在(x,y,z)=(0,6,12)(单位：m)处受集中荷载.我们考虑两种工况.工况1的集中荷载为：f1(t)=Csin(πt/2)/(t+1)，工况2的荷载为：f1(t)=Csin(πt/2)，其中常数C=1×106N，荷载作用方向如图9所示.动力计算总时长T=10 s，时间步长为Δt=0.05 s.选用α=0.25，β=0.5的Newmark-β法计算有限元模型动力响应，为了加速代理模型的计算和便于模型的预测效果分析，对代理模型在训练阶段的数据进行了选取处理，即选取图9所示的各构件连接点及连接点附近的节点所对应的动力响应作为模型的训练数据，共选取节点数m=142，对应自由度数为md=426.由于有限元离散模型的节点数与选取的输入节点数目相差较大，数据预处理参数选择p=5，nB=50.图9中使用空心圆节点标注的位置仅代表代理模型的预测解与有限元计算参照解的对比位置，实际上代理模型的输出结果为模型输入的所有节点所对应的下一时刻的动力响应.对于该三维问题，同样采用前10%计算时长的有限元计算结果来构造训练集，进行非线性预处理和建立代理模型.

图9 动力学响应预测的3D空间框架模型及解观测节点选择Fig.9 3D spatial frame structure and selection of observation nodes for dynamic response prediction

为清晰起见，图10给出结构工况1时在t=1 s的框架结构及观测节点附近的有限元网格剖分及变形情况，其中白色虚线方框表示预测解和参照解进行对比的具体范围.图11为代理模型在不同工况下对4个观测点的时程动力分析位移预测情况.可以看出基于数据非线性预处理的贝叶斯回归代理模型的预测位移与参照解吻合情况良好，同时4个观测点响应数据幅值依次降低，与图10所示的模型整体变形相符.

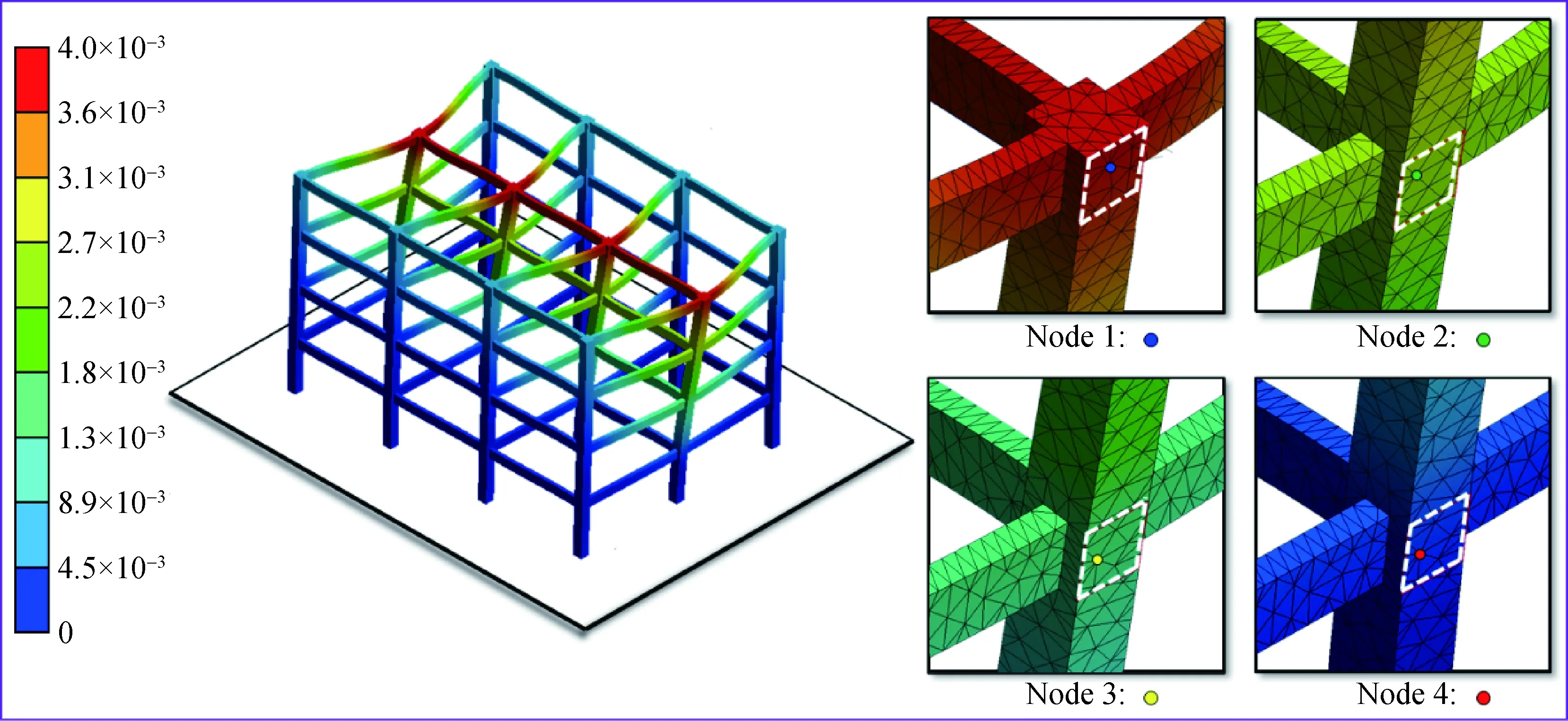
图10 空间框架及观测节点局部区域t=1 s时刻位移预测解(单位: m)Fig. 10 Displacement prediction for the spatial frame structure and regions near observation nodes at t=1 s(unit: m)

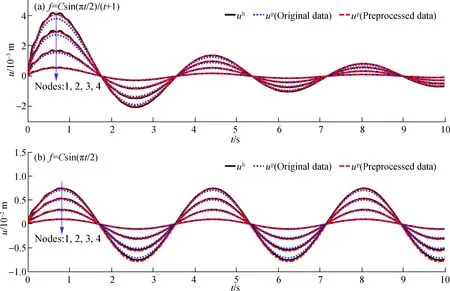
图11 空间框架观测点动力响应预测结果对比Fig.11 Comparison of dynamic response prediction results at observation nodes for the spatial frame structure

图12 空间框架观测点局部区域动力响应代理模型预测解与有限元数值解对比(单位: m)Fig.12 Comparison between the predicted solutions by surrogate model and the numerical solutions by finite element dynamic analysis near observation nodes for the spatial frame structure (unit: m)

为了进行代理模型和直接有限元分析的效率对比，表1列出了框架问题的各部分计算耗时，计算平台为Amd 3600 CPU及NVIDIA GeForce RTX 2080S.通过计算时间对比可以发现，相比于直接的有限元动力计算分析，基于数据非线性预处理的结构动力响应贝叶斯回归代理模型可以大幅减少计算时间，显著提高计算效率.

表1 空间框架问题的有限元动力分析和代理模型预测计算效率对比

5 结 论

在有限元结构动力分析中，网格细化可以提高空间离散的精度但会降低时程分析的步长，降低计算效率.为了提升有限元结构动力计算效率，本文基于有限元节点形函数的影响域范围对输入数据进行提炼和压缩，通过引入激活函数先将输入数据进行归一化非线性处理，然后利用非负B样条基函数对数据进一步进行扩展处理，提高关键节点的预测精度.最后，将经过非线性预处理的数据集和贝叶斯回归方法相结合，提出了一种结构动力响应的贝叶斯回归代理模型.数值结果表明，基于数据非线性预处理的结构动力响应贝叶斯回归代理模型的动力预测结果与直接有限元动力分析结果吻合良好，且能够大幅提高结构动力响应分析的计算效率.