考虑结构质量未知的非链式结构系统识别方法

林 英，陈泽宁，雷 鹰*

(1.厦门城市职业学院建筑工程学院,福建 厦门 361008;2.厦门大学建筑与土木工程学院，福建 厦门 361005)

目前国内外已发展了许多基于结构振动响应进行结构系统识别的方法，但这些方法大都是用结构已知的质量信息，对结构刚度、阻尼等参数进行识别和损伤评估[1-4].然而，结构在服役中，其质量可能会发生变化，或者不易确定与测量.如：雪荷载使结构质量增加，混凝土结构中，水分的吸收使结构质量增加[5]，建筑结构中为满足使用而布置的设备、物品等.以上因素使结构质量发生改变.此外不准确的质量信息也会导致错误的结构识别结果[6].因此，需要研究在结构质量未知下的结构系统识别.虽然目前有部分学者提出了质量未知下结构识别和损伤诊断方法.如Nayeri等[7]和Masri等[8]提出恢复力方法，识别链式结构质量归一化刚度参数.Zhan等[9-10]进一步提出了链式系统的质量归一化刚度解耦，独立识别结构质量和刚度变化.de Angelis等[11]利用识别的结构状态，求解结构质量、刚度等参数，但需对结构中任意一个自由度同时安装传感器和激振器，并在其余每个自由度放置传感器或者激振器.Mukhopadhyay等[12]利用结构外激励和响应信息，识别剪切结构质量、刚度等物理参数.Zhang等[13]提出利用子结构的运动方程进行循环识别，估算未知质量剪切型子结构的质量归一化参数.Huang等[14]在扩展卡尔曼滤波(EKF)中引入能量平衡，估计结构刚度和质量，但需要观测外激励和所有自由度加速度，并重建结构速度和位移响应.Xu等[6,15-16]提出质量未知下的结构非线性识别系列方法.但上述这些方法主要适用于较简单的链式结构，且往往需要观测结构全部自由度加速度、速度和位移响应.对于非链式结构，由于其并非像链式结构一样具有集中质量矩阵，在利用EKF时，结构状态方程和观测方程无法对质量求偏导，因此对质量未知的非链式结构系统识别研究还很少.

虽然目前已开展了未知外部激励下结构系统的识别[17-19]，但研究的均是结构质量已知的情况.Liu等[20]研究了未知地震激励下质量及结构恢复力无参数化识别，Lei等[21]也研究了在未知环境激励下的基于部分加速度响应识别结构单元质量和刚度变化，但这些方法也仅适用于链式结构.

本文针对目前相关研究存在的不足，考虑了结构质量未知的非链式结构在已知外激励和未知外激励下的识别，分别基于EKF方法和作者最近提出的未知激励下的EKF(EKF-UI)方法，识别结构状态与未知的结构质量、刚度和阻尼参数，并通过梁结构数值模型，验证提出的两种方法的有效性.

1 本文提出的两种方法

1.1 已知激励下基于EKF的质量未知非链式结构系统识别

结构质量未知时，n个自由度的非链式结构在已知激励下的运动方程为：

(1)

将结构参数扩展到结构状态向量组成系统增广向量，即

(2)

式中θ包含结构单元线刚度和阻尼参数.

由增广状态向量(2)可以将结构运动方程(1)转化为状态方程：

g(Z,f)+w,

(3)

其中：w为均值为0的模型误差项，其协方差矩阵为Q.

观测方程可以表示为：

h(Zk+1,f)+vk+1,

(4)

其中：yk+1为t=(k+1)Δt(Δτ是采样时间间隔)时刻的加速度响应观测向量；νk+1为白噪声形式的误差向量，其协方差矩阵为Rk+1.

(5)

(6)

其中

(7)

假设结构阻尼为比例阻尼，并利用M(θ)M(θ)-1=I，得：

(8)

则有：

(9)

(10)

EKF方法包括时间更新和测量更新.第一步对结构状态向量进行时间更新，

(11)

其误差协方差为：

(12)

其中Φk|k≈I+ΔtGk|k.

第二步是对状态预测值进行修正：

(13)

相应的误差协方差为：

(14)

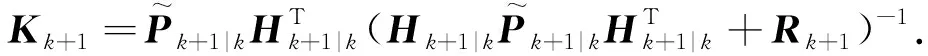
1.2 未知激励下基于EKF-UI的质量未知非链式结构系统识别

结构质量信息和外激励均未知时，n自由度非链式结构在未知激励下的运动方程为：

(15)

其中fu是结构所受的未知外激励,ηu为未知激励作用位置矩阵.

g(Z,fu)+w.

(16)

观测方程为：

yk+1=h(Zk+1,fu)+vk+1.

(17)

对结构状态方程(13)和观测方程(14) 进行一阶泰勒展开：

(18)

(19)

其中：

(20)

(21)

(22)

(23)

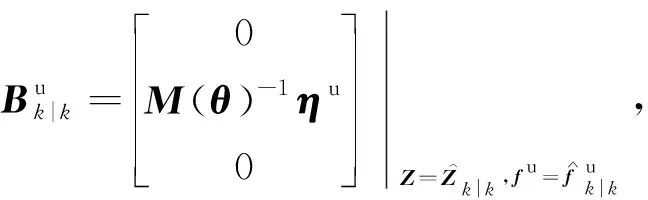
(24)

(25)

结构状态随观测值不断更新：

(26)

式中Kk+1为卡尔曼增益矩阵.

(27)

(28)

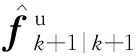
(29)

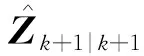
(30)

状态预测值的误差协方差为：

Qk.

(31)

值得注意的是，在激励未知且质量未知的情况下，结构参数无法求得唯一解.因此，需假设结构激励处自由度某个相邻单元的质量为已知，结构参数可有唯一解.此外，仅观测加速度响应时，由于测量噪声的存在，使得在估计结构位移时会出现漂移现象.本文通过加速度与应变响应的数据融合，解决漂移问题.

2 数值算例

为验证提出方法的有效性，以梁结构的数值算例，分别在外激励已知和外激励未知情况下，应用EKF和EKF-UI对质量未知的非链式结构系统进行识别.

2.1 外激励已知质量未知的非链式结构参数识别

图1所示简支梁，梁长15 m，横截面尺寸为0.15 m×0.06 m，弹性模量为E=2.06×1011N/m2，各单元线质量为70.20 kg/m，各单元线刚度为3.708×106N·m，沿梁长方向划分10个单元，记为编号①～⑩，共有11个单元节点.阻尼为瑞利阻尼，α=0.592 7，β=9.718×10-4.在结构第4节点处施加一个竖向白噪声激励F.

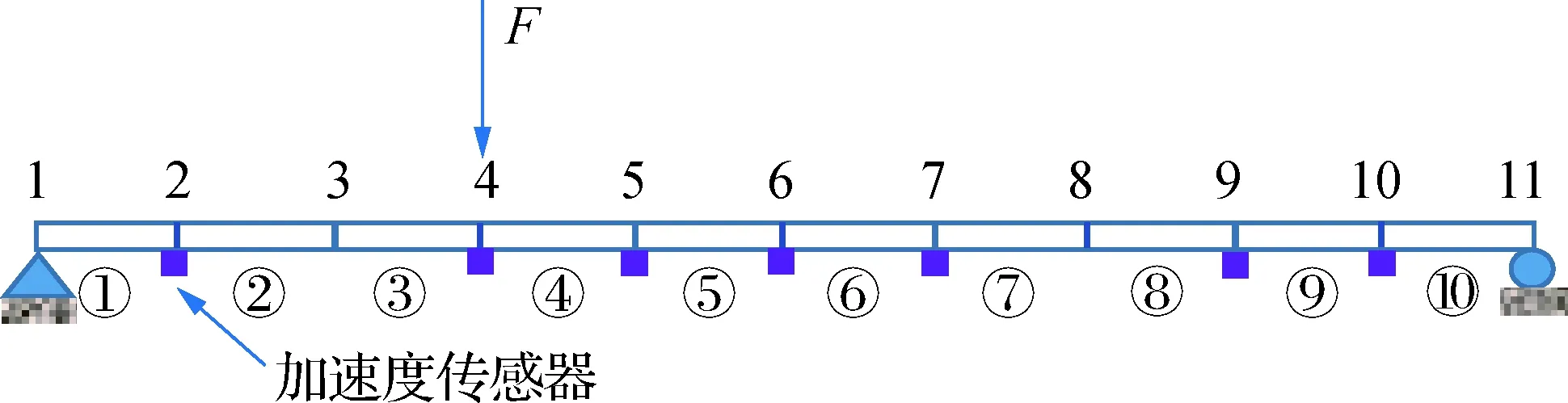
图1 已知外激励下简支梁Fig.1 Simple supported beam

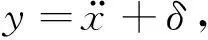
假设各个单元的线质量、线刚度、阻尼系数的初始值均为真实值的70%.利用质量未知情况下的EKF方法对结构线质量、线刚度、阻尼系数和结构状态同时进行识别.图2和图3分别为结构第5节点的速度、第8节点的位移识别结果，由图可见，所提方法对结构响应的识别与真实情况能够很好符合.

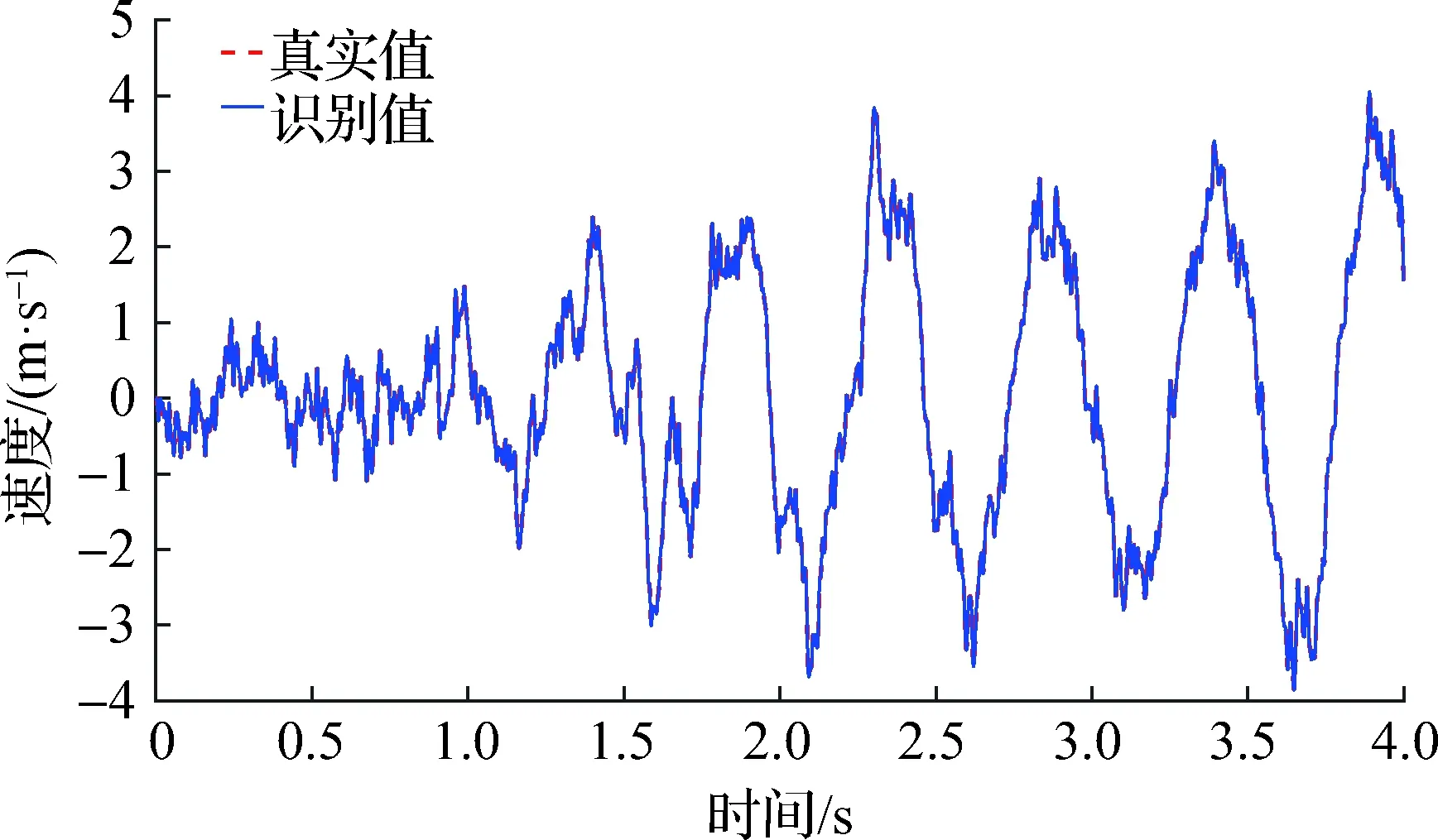
图2 第5节点速度

图3 第8节点位移

结构第5和第9单元的线质量、第3和第6单元的线刚度识别值如图4和5所示；结构阻尼系数α、β的识别值如图6所示，结果表明质量、刚度和阻尼的识别均能很快收敛到真实值.

图4 第5(a)和第9(b)单元线质量识别结果Fig.4 Identification of the line quality in element 5 (a) and 9 (b)

各单元的结构参数识别结果以及识别误差如表1所示，结构各参数的识别误差均不超过1%，验证了本文所提出的质量未知下的EKF方法，对于已知激励作用下的质量未知的非链式结构有很好的识别精度，能在部分观测并且考虑观测噪声情况下，同时识别出结构质量、刚度、阻尼及结构响应，具有良好的抗噪性.

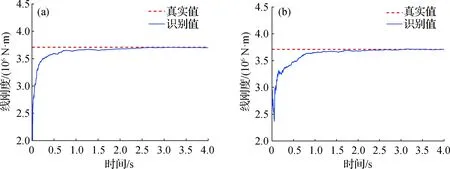
图5 第3(a)、6(b)单元线刚度识别结果Fig.5 Identification of the line stiffness in element 3 (a) and 6 (b)

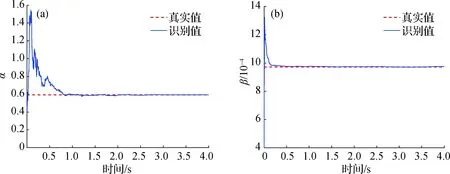
图6 阻尼系数α(a)、β(b)识别结果Fig.6 Identification of the damping coefficient α (a) and β (b)

表1 白噪声激励下简支梁结构参数识别结果

2.2 外激励和质量未知的非链式结构参数识别

图7所示一个简支梁，全长2 m，单元长度均为L=0.4 m，共计10个自由度；结构参数为：截面为0.05 m×0.015 m矩形，各单元线密度为mb=6.075 kg/m，弹性模量为E=2.06×1011N/m2，单元线刚度为EI/L=7 242.187 5 N·m.结构第2自由度位置受到一个未知的竖向外激励F.①～⑤是单元编号，1～10是节点自由度编号.

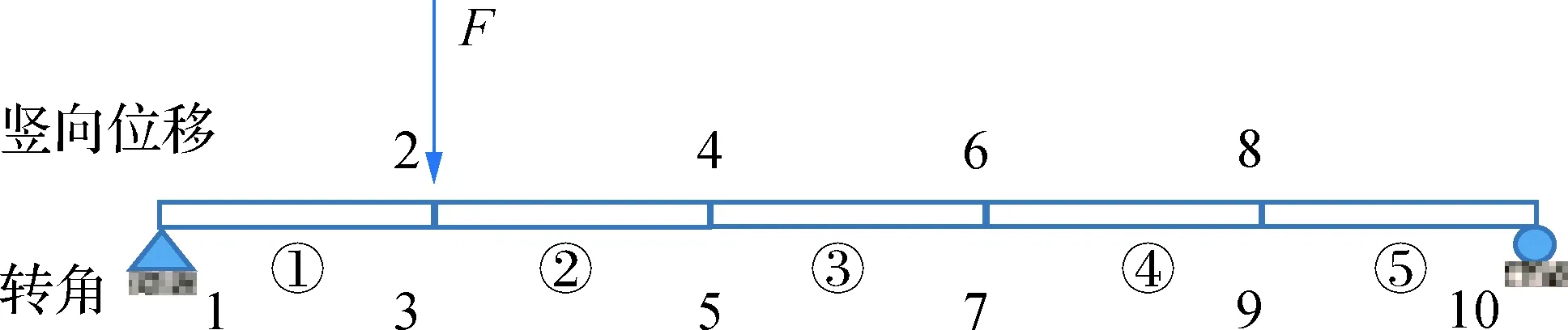
图7 5单元简支梁模型Fig.7 Model of simple supported beam with 5 elements

仅观测第2、4、6、8的自由度竖向加速度及所在节点应变，并考虑响应受1%的噪声污染.由于外激励是未知的，如果外激励附近单元质量也未知，将无法识别得到唯一解.因此，为保障有唯一解，需假设外激励附近的第①和第②单元线密度已知，其余单元初始线密度为真实值的90%.通过未知激励下质量未知的EKF-UI方法对结构参数进行识别. 各单元线密度和线刚度的识别结果如图8、9和表2所示.各参数的识别值很快能够逼近收敛于真实值，最大误差不超过1.5%，在测量噪声情况下，具有很好的识别精度和良好的抗噪性，验证了所提方法的有效性.

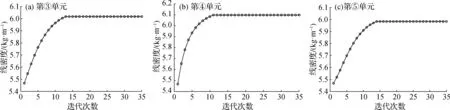
图8 单元线密度识别结果Fig.8 Identification of the line quality in elements

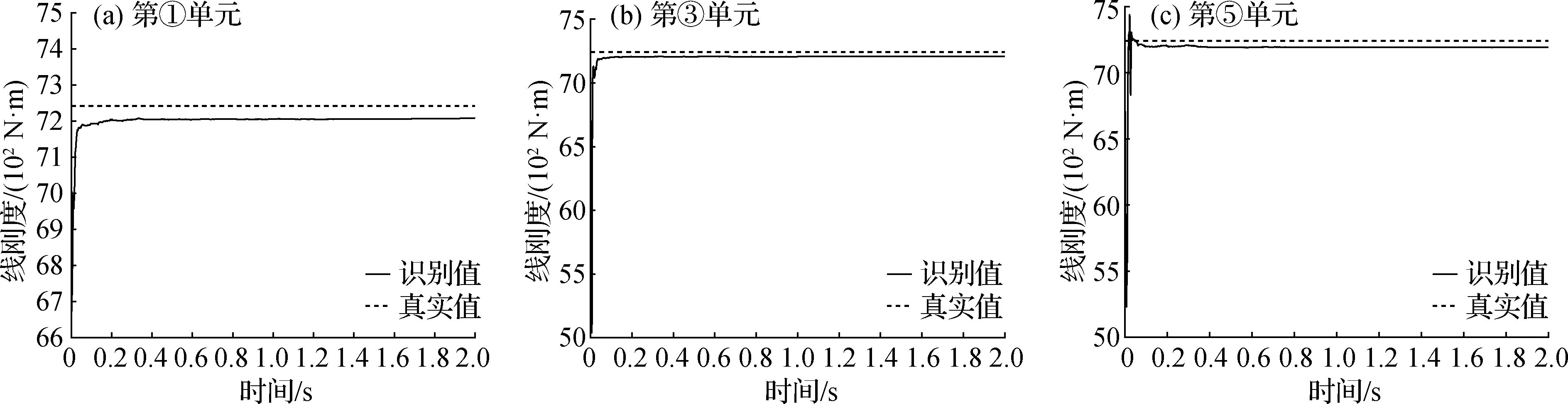
图9 单元线刚度识别结果Fig.9 Identification of the line stiffness in elements

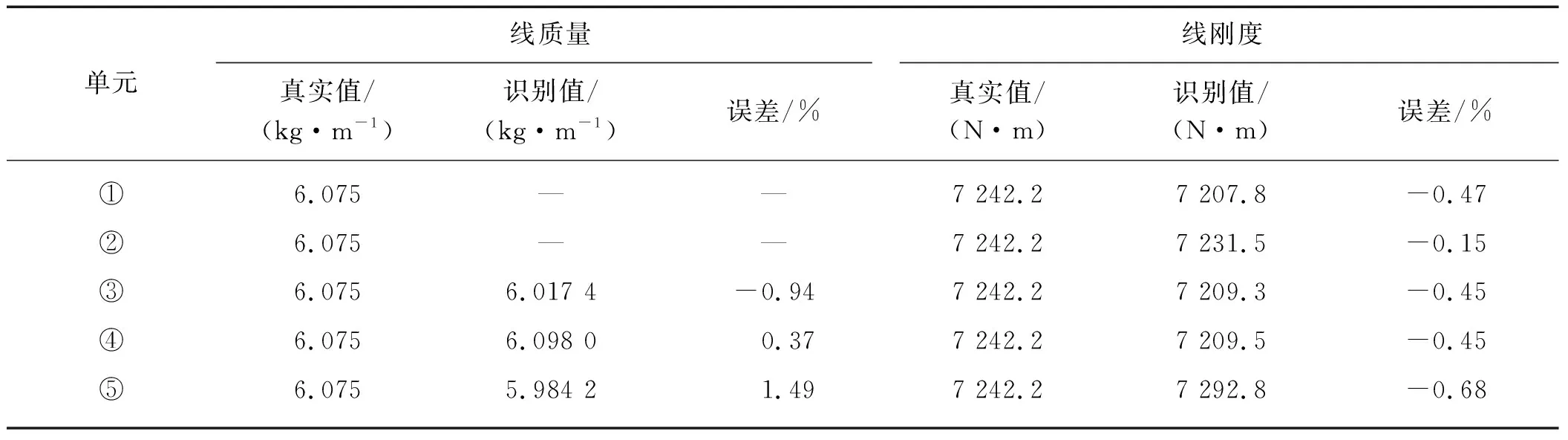
表2 结构单元线刚度、线质量识别值及其误差

3 结 论

本文首先提出了已知结构外激励下结构质量未知的非链式结构系统的识别方法，该方法基于EKF方法，可仅观测梁结构的部分加速度响应，通过将结构质量逆矩阵关于未知质量参数的偏微分转化为结构质量直接对未知质量参数的偏微分，可以得到线性化的结构运动方法及结构加速度响应观测方程，进而同时识别结构的位移速度响应状态与未知的结构质量、刚度、阻尼参数.进一步推广研究在外激励未知情况下，基于发展的EKF-UI方法，融合观测的结构部分加速度与应变响应，同时识别结构的位移速度响应状态与未知的结构质量、刚度和阻尼参数.提出的两种方法分别通过梁结构在已知和未知外激励下结构系统识别的算例，验证了提出的两种方法能有效准确识别结构响应状态与未知的结构质量、刚度与阻尼参数.

本文所提出的方法在其他复杂的未知质量的结构系统识别的应用，包括未知地震作用下非线性结构系统识别，还值得进一步的研究.