方位多通道滑动聚束SAR通道相位偏差估计方法*

王 宽， 毋 琳， 李 宁

(1.河南大学 计算机与信息工程学院，河南 开封 475004；2.河南大学 河南省大数据分析与处理重点实验室，河南 开封 475004；3.河南大学 河南省智能技术与应用工程技术研究中心，河南 开封 475004)

0 引 言

星载方位多通道合成孔径雷达(synthetic aperture radar，SAR)系统在方位向上结合数字波束形成(digital beamforming，DBF)技术，可以克服最小天线截面积的限制，实现高分辨率和宽测绘带(high resolution and wide swath，HRWS)成像[1,2]。此外，方位多通道SAR系统还可以采用与滑动聚束模式相结合的方式对地进行观测，在获得超高分辨率的同时仍然保证大的距离测绘带宽[3,4]。

在实际的星载SAR系统中，不可避免地通道间幅相特性不一致将大大降低DBF的解模糊性能。其中，通道间的幅度偏差通过使用幅度均衡方法可以有效地校正[5,6]。针对通道间的相位偏差校正问题，目前，学者们提出了一些行之有效的解决方法[7～10]。然而，由于多通道滑动聚束SAR模式下波束在方位向上的渐进扫描，导致传统的通道误差估计方法不再适用。针对这一问题，Fan H T等人[11]在经典方位互相关方法的基础上考虑了波束旋转的影响，提出了一种多通道滑动聚束SAR系统通道相位偏差校正方法。Gao H L等人[12]基于频谱优化原理，提出了一种基于最小熵的方法对相位偏差进行估计。然而，上述方法通常要求多普勒中心精确已知，这将在实际处理中引入繁琐的估计过程，且估计精度有限。

本文提出了一种基于重构多普勒谱分析的方位多通道滑动聚束SAR通道相位偏差估计方法。通过分析得到相位偏差会导致重构后的方位多普勒谱产生跳变，基于相位偏差与跳变幅度之间的关系，通过优化多普勒谱，可以得到相位偏差估计值，在多普勒中心未知的情况下仍然有效。仿真实验和实验对比结果验证了方法的有效性和稳健性。

1 方位多通道滑动聚束SAR模式

1.1 回波信号模型

在方位向上具有3个接收通道的星载方位多通道滑动聚束SAR系统工作几何模型如图1所示。其中，中间孔径(Tx)发射线性调频信号，3个接收孔径(Rx)同时接收地面回波，可以得到3个通道的回波数据。此外，通过控制方位波束主动扫描，可以获得相较于传统条带模式更大的合成孔径时间，提高方位向分辨率。

图1 星载方位多通道滑动聚束SAR模式示意

三通道滑动聚束SAR回波平面几何模型如图2所示。假设在正侧视情况下，坐标原点选择为卫星整个照射时间的中心处，ωr为方位波束扫描角速度，卫星以恒定速度v沿方位向飞行，波束在扫描过程中聚焦在一个虚拟旋转点O′处，Rrot为雷达到虚拟点的最短斜距，r为雷达到场景的斜距。方位波束扫描造成方位分辨率的改变，其改变因子A为

A(r)=1+r×ωr/v

(1)

图2 方位多通道滑动聚束SAR回波平面几何模型

假设方位多通道滑动聚束SAR系统具有N个通道，则第i个接收天线接收到的位于(r,x)的点目标方位向的回波信号可以表示为

(2)

(3)

式中σ(r,x)为(r,x)处目标的后向散射系数，t为方位向时间，rect[·]为窗函数，Δxi为第i通道与参考通道之间沿航向的距离，λ为波长，Lf为波束在地面的“足印”长度，Tb为方位总照射时间。

1.2 方位回波时频关系

星载方位多通道滑动聚束SAR的回波频谱由于波束渐进扫描和多通道采样的特点而具有一定的特殊性。其与传统条带模式的区别主要体现在方位向上,如图3所示。其中，f表示方位多普勒频率，Ba，Bs和Bb分别表示点目标多普勒带宽、方位波束带宽和方位向总带宽，PRF为系统脉冲重复频率，Ta为每个点目标的照射时间。由于波束的恒速扫描，目标的多普勒中心频率随方位位置的不同呈现一个线性关系，用krot表示多普勒中心随时间的变化率可以表示为

(4)

图3 方位多通道滑动聚束SAR回波方位时频关系

多通道SAR系统通道间的相位偏差会严重影响DBF的重构性能，通过对重构后的多普勒谱进行优化，可以得到相位偏差估计值。然而，由图3可知，在方位多通道滑动聚束SAR中每个点目标的方位多普勒带宽是按照Nyquist采样定律进行采样的，但在整个波束照射时间Tb内，方位向总的多普勒带宽超过了N×PRF的总方位采样率。所以，方位多通道滑动聚束SAR模式的回波频谱同时包含来自波束旋转和信号非均匀采样造成的频谱混叠，传统的多通道条带SAR模式的通道相位偏差方法也将不再适用。

2 方位多通道滑动聚束SAR相位偏差估计方法

2.1 总体架构

本文提出了一种用于方位多通道滑动聚束SAR系统的通道相位偏差估计方法。首先，使用两步式聚焦技术中的“去斜”操作去除由于波束扫描造成的多余旋转带宽，经过快速傅里叶变换(fast Fourier transform,FFT)后通过方位重构滤波得到重构多普勒谱；然后，通过分析相位偏差对重构多普勒谱特性的影响，使用相邻频谱分量间的跳变幅度定量描述多普勒谱的变化；最后，构造目标优化函数，提出一种最优化理论得到相位偏差估计值。本文方法的处理流程如图4所示。

图4 本方法的处理流程

2.2 方位多普勒谱重构

每个方位通道的去斜函数h1,i(n·Δt′)可以表示为

(5)

式中 Δt′=1/PRF，Na为每个方位通道的采样点数。将所有通道的回波经FFT变换到方位频域进行滤波重构。去斜后的多通道SAR信号的系统响应由矩阵H(f)表示

(6)

通过对矩阵H(f)求逆，可以得到重构滤波器P(f)

P(f)=H-1(f)=[P1(f),P2(f),…,PN(f)]T

(7)

在实际的星载SAR系统中，通道间的相位不一致性是不可避免的，假设通道间的相位偏差用Γ表示，方位信号的重构过程可以表示为

(8)

式中e为存在相位误差，0(f)=[S0,1(f),S0,2(f),…，S0,N-1(f)]T，Γ-1=diag{x}=diag{ejζ0,ejζ1,…,ejζN-1},Se(f)=[Se,1(f),Se,2(f),…,Se,N-1(f)]T。

经过加权求和可以得到无模糊的方位多普勒谱

(9)

式中 [·]H为共轭转置。

2.3 “通道偏差—重构多普勒谱”解析关系

由式(9)可以看出，重构多普勒谱中的能量来自各接收通道信号的频谱分量。在无通道相位偏差的影响下，各通道频谱分量相等，重构后可以得到平滑的无模糊多普勒谱。然而，通道间的相位偏差将会严重影响DBF技术的重构性能，导致各频谱分量的能量不再相等，在拼接处出现明显的跳变。令Hs(f)=Pn(f)diag{Se(f)}=[hs,0(f),hs,1(f),…,hs,N-1(f)]H，可以得到相邻频谱分量之间的跳变幅度与相位偏差的关系

(10)

式中l为取跳变点两侧频谱分量的采样点数，E{·}为数学期望。由式(10)可以得到相位偏差与多普勒谱跳变幅度的关系如图5所示。

图5 相位偏差与频谱跳变关系

2.4 基于最优化理论的相位偏差求解

由图5可知，通道相位偏差为0时，重构多普勒谱平滑，无跳变现象，可以构造目标优化函数

(11)

3 实验验证

3.1 有效性验证

通过非均匀地物场景仿真实验对所提方法进行验证，主要仿真参数如表1所示。在模拟中，通道1被设置为参考通道，l的取值为100个采样点，每个通道附加的相位偏差分别为0°,25°和45°，利用所提方法得到各通道间的相位偏差分别为0°,25.87°和45.81°，估计误差在1°以内，具有较高的精度。将估计结果用于相位偏差补偿后，使用方位重构方法进行多普勒谱重构[4]，经过传统的CS成像算法处理后即可得到聚焦的SAR图像。存在相位偏差情况下的成像结果如图6(a)所示，可以清楚地看到图像中存在明显的模糊分量，特别是圆圈标注的区域，严重降低了SAR图像的质量。图6(b)为使用本文方法对相位偏差矫正后的结果，图像中的模糊分量得到了很好地抑制。这说明了本文所提方法对通道间相位偏差的估计具有较高的精度，并对最终聚焦的SAR图像质量有着很大的改善。

表1 仿真参数

图6 聚焦后的SAR图像

3.2 性能对比分析

利用Mento-Carlo实验对比分析本文方法与文献[11]方法在不同信噪比下的相位偏差估计性能，采用平均均方根误差(average root mean square error,ARMSE)描述相位偏差的估计性能[9]，实验次数为100次。图7为上述两种算法在不同信噪比下的ARMSE曲线。可以看出，相位偏差估计精度随着信噪比的增大而增大，与文献[11]方法相比，本文方法具有更高的精度，特别是在低信噪比的情况下。

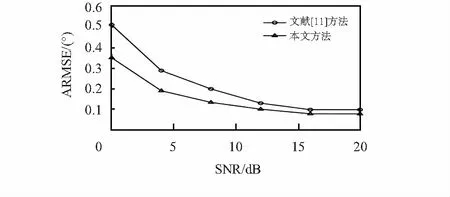
图7 算法性能对比

4 结 论

本文提出了一种星载方位多通道滑动聚束SAR系统通道相位偏差估计方法，将两步式聚焦技术的“去斜”操作与DBF技术结合，解决了方位频谱的混叠问题；提出了一种最优化理论通过求解重构多普勒谱中跳变的最小值，可以成功地估计通道间的相位偏差。仿真实验和方法性能对比表明了所提方法的精确性和稳健性。