基于单目视觉的无人水面艇目标跟踪方法*

饶六中， 王建华， 郑 翔， 张山甲

(上海海事大学 航运技术与控制工程交通行业重点实验室,上海 201306)

0 引 言

无人水面艇(unmanned surface vehicle,USV)是一种新型的无人化水上智能作业平台，具备小型轻量，机动灵活等优势[1]，适用于执行危险、狭窄水域等情况下的任务。在无人水面艇领域，对水面目标的跟踪是研究热点之一，具有十分广泛的应用前景，例如无人水面艇主从式编队作业、水面目标抵近监视与跟踪、航运服务等。特别在弱联通的狭窄河道水域，无人水面艇之间互为中继节点实现与岸基的通信[2],这一应用为无人水面艇的目标跟踪提供了工程应用价值。

近十几年来，视觉跟踪技术取得长足进步，研究人员提出许多有效的视觉目标跟踪算法[3]。针对文献[4]提出的传统纯方位目标跟踪算法存在较大跟踪误差的问题，文献[5]提出利用计算机视觉技术分析被跟踪船航行图像，计算被跟踪船航向和位置信息，该方法有效降低跟踪误差。

无人水面艇的目标跟踪根据使用领域不同分为实体目标跟踪和图像目标跟踪[6]。基于图像目标跟踪的应用，文献[7]提出一种基于立体视觉的方法估计运动中无人水面艇的位置、速度和航向，该方法将简单的立体视觉匹配算法与扩展卡尔曼滤波的预测校正方法相结合实现无人水面艇对被跟踪船的跟踪；文献[8]提出基于单目视觉的自动特征提取和跟踪滤波算法，对被跟踪船进行实时检测和跟踪，利用相机图像中地平线到被跟踪船的像素距离计算出距离信息，最终利用无人船对被跟踪船进行跟踪实验；文献[9]通过处理高清图像获得高精度的被跟踪船距离，在提取的感兴趣区域上，对原始图像进行立体匹配，为被跟踪船的定位提供准确的三维信息，最终提出将基于二维图像的目标跟踪与约束模板匹配相结合计算深度的方法，对被跟踪船进行跟踪；文献[10]提出融合HOG与颜色特征进行运动目标跟踪；文献[11]通过将经典的跟踪方法Mean-Shift搜索模型和卡尔曼(Kalman)滤波预测模型用于水面图像中目标位置信息跟踪。

结合国内外文献发现,在非均匀流场下的水面目标跟踪研究较少，但流场干扰在实际河道中不可忽略，因此，本文提出一种基于单目视觉的无人水面艇目标跟踪方法。首先，描述了无人水面艇在不均匀流场干扰下的平面运动方程；然后，通过对运动状态下标志物的检测提出视觉跟踪方法；在不均匀流场干扰下，利用实验室自主开发的无人水面艇实验平台进行仿真实验，验证本文所提方法的有效性和正确性。

1 目标跟踪问题描述

为成功地跟踪上被跟踪船，需要获得被跟踪船相对于跟踪船的距离和方位信息。假设跟踪船与被跟踪船机动性能相同，跟踪船利用单目相机对被跟踪船船尾搭载的标志物进行检测并保持限定距离跟随被跟踪船，最终分析不均匀流场干扰和不同目标路径对跟踪轨迹误差和航向误差的影响。

1.1 跟踪船运动模型

跟踪船运动模型的建立是基于课题组自主研制的固定双桨无人水面艇“海翔”号，该艇长1.6 m，宽1.2 m，最大航速可达4节，无艏侧推器和舵，主要通过调节两侧推进电机螺旋桨的转速对无人水面艇进行控制[12，13]。

无人水面艇在抛物线型流场干扰下跟踪被跟踪船的示意图如图1所示，其中无人水面艇作为跟踪船搭载单目相机，被跟踪船船尾搭载标志物。为表述跟踪船的速度、航向以及位置等信息，本文建立世界坐标系XwOwYw和跟踪船附体坐标系xoy描述跟踪船水平运动特性。

图1 跟踪问题示意

其中，Yw轴与正北方向平行，Xw轴与正东方向平行；附体坐标系原点O与无人艇重心G重合；u为无人艇在附体坐标系中沿x轴的航速，v为无人艇在附体坐标系中沿y轴的航速；Fl，Fr分别为无人水面艇左右螺旋桨产生的推力；Xflow，Yflow分别为流作用于艇体的流体动力；Nflow为流体作用于艇体的力矩；Vflow为抛物线型流场的流速；d为无人水面艇的宽度；ψ为无人水面艇的艏向角，取正北方Y轴方向为0°；f为无人水面艇行驶中所受所有阻力之和。本文仅考虑无人水面艇的前进，艏摇，横漂运动，忽略艇的垂荡、横摇、纵摇运动得出如下平面运动方程[14]

(1)

式中m为无人艇的总质量；J为艇的转动惯量；ω为转动角速度；fl，fr分别为艇体左右两侧所受的阻力；ψ0为无人水面艇的初始艏向角。

1.2 流场模型

本文假设天气情况良好，在内河航道水域只存在流场干扰的情况下，仿真验证跟踪船对被跟踪船的跟踪性能。通常情况流速沿航道纵向变化不大，但航道横断面分布不均匀，一般航道中心流速最大，向两侧逐渐减小，本文结合实际建立如图2所示的流场模型，流速分布纵向不变，横向沿航道以抛物线型分布，流向与航道平行。

图2 流场模型

上述流场模型的公式表达如下

(2)

式中 2Pflow为峰速，Wflow为流场宽度。

2 基于单目视觉的无人水面艇目标跟踪方法

2.1 被跟踪船标志物检测方法

图像中目标对象识别主要基于目标对象的颜色、纹理和形状三个属性。为更准确识别被跟踪船标志物，所选特征应不易受运动状态的改变而影响，因此,本文选用目标对象的颜色属性进行检测。为简化描述过程，本文只针对红色特征的标志物进行检测流程的说明。首先将采集到的红色标志物由三原色(RGB)颜色空间转换到HSV颜色空间，如图3(a)所示；在HSV颜色空间确定标志物的颜色阈值范围并进行二值化处理，效果如图3(b)所示；从图3(b)可以看出存在一定的噪点，需要对图像进行降噪处理。文献[15]使用自适应中值滤波图像去噪方法，通过自适应改变滤波窗口大小，有效降低了非噪声点误判为噪声点的概率，本文应用该方法后的处理效果如图3(c)所示，图像中的噪声点被有效去除；最终，初始化标志物轮廓质心，确定图像中标志物面积最大的轮廓的外接矩形，检测出标志物在图像中的位置，效果如图3(d)所示。

图3 图像处理效果

2.2 视觉跟踪原理

跟踪船对被跟踪船船尾搭载的标志物进行动态跟踪时，需要实时获取被跟踪船相对跟踪船的方位和距离，本文选择标志物图像的几何中心位置与标志物期望图像进行对比来获取方位误差和距离误差。跟踪船只与标志物位置关系如图1所示。为了更好说明本文提出的视觉跟踪原理，定义虚拟航线AcB垂直于标志物几何中心表面，跟踪船搭载的单目摄像机光轴与跟踪船航向相同。定义摄像机光轴水平方向偏离标志物图像几何中心的角度为偏航角θc，跟踪船偏离虚拟航线的距离为偏航距离D，本文将偏航角和偏航距离作为控制器的输入量进行目标跟踪。

2.2.1 偏航角的计算

标志物图像与期望图像的几何位置关系如图4所示，其中,θc为偏航角，θc(-)为标志物的几何中心在摄像机图像坐标的左侧，θc(+)为标志物的几何中心在摄像机图像坐标的右侧。

图4 偏航角计算

偏航角θc定义为标志物图像的几何中心X1与期望图像的几何中心Xc的差值与相机焦距的比值

θc=arctan((X1-Xc)/f)

(3)

式中f为摄像机焦距，假设标志物图像的几何中心X1与期望图像的几何中心Xc的横坐标相等。

2.2.2 偏航距离的计算

在不考虑相机镜头畸变的情况下，根据小孔成像模型可以计算出相机沿光轴方向到实际标志物几何中心X1的距离Z，其计算公式为

(4)

其中，H为实际标志物的高度，h为标志物图像与X1横坐标处的垂直像素高度。在附体坐标系下，实际标志物相对于跟踪船的位置可以由偏航角θc和距离Z计算得出

(5)

在跟踪过程中，虚拟航线始终垂直于标志物表面，可以通过检测标志物图像左右两侧边界确定标志物图像的几何中心Ac，在附体坐标系下，如图1所示，以船体中心为坐标原点，设标志物几何中心为Ac，在虚拟航线上任取一点B，则偏航距离D可具体表达为

(6)

利用偏航距离可以判断出跟踪船与标志物的相对位置关系，当D<0时跟踪船位于虚拟航线右边，当D>0时跟踪船位于虚拟航线左边。

2.3 性能评估

(7)

(8)

式中Δ1=Xi-Xobji，Δ2=Yi-Yobji，Δ3=xi-Xobji，Δ4=yi-Yobji，(Xi,Yi)为跟踪船在第i个跟踪点的位置；(Xobji,Yobji)为期望路径在第i个跟踪点的位置；(xi,yi)为被跟踪船在第i个跟踪点的位置，ψusvi为跟踪船在第i个跟踪点的航向；φusvi为被跟踪船在第i个跟踪点的航向。

3 仿真实验

仿真实验基于“海翔号”的视觉系统，搭建仿真实验平台，其中,跟踪船搭载的摄像机内参矩阵为[1 050,640,0;0,1 050,512;0,0,1]，像素焦距为1 050，图像分辨率为1 280像素×1 024像素，标志物的大小为2 m×1 m。仿真实验结合大多数实际河道宽度、不同季节流速不同的情况，设计不同流速干扰和不同期望路径验证本文提出视觉跟踪算法的跟踪性能，仿真忽略船的垂荡、横摇、纵摇运动，只考虑跟踪船在水平面内的运动。

3.1 抛物线型流场干扰下直线路径的目标跟踪

为了直观地观察和分析抛物线型流场干扰对直线路径下目标跟踪的影响，仿真实验设计了流向为0°，宽度为35 m不同峰速的抛物线型流场，目标路径为起点坐标(0,50)m，终点坐标(35,85)m的直线，整个运动过程的仿真结果如图5所示。

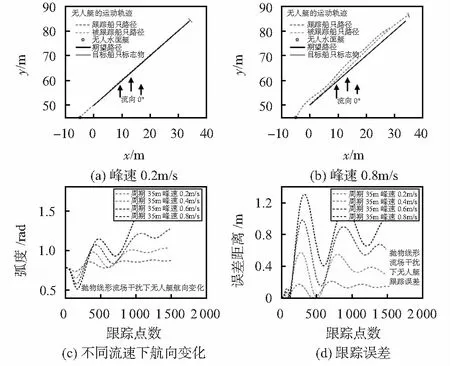
图5 流场干扰下直线路径的目标跟踪

由图5(a)，(b)可以看出，在同类型流场下，随着峰速的增大，跟踪船的跟踪轨迹与被跟踪船的跟踪轨迹整体向流向的方向偏移。由图5(c)，(d)可以看出，随着峰速的增大，跟踪船的航向变化逐渐增大，并向流向的反方向偏移,反映在轨迹上就是跟踪精度的下降。Tend时刻，当流场流速在0.8 m/s以内，跟踪船的平均跟踪误差为0.507 m，平均航向误差为9.98°，以上仿真结果表明在流场干扰下跟踪船能够较好跟踪上被跟踪船标志物，具有一定的抗干扰性。

3.2 抛物线型流场干扰下回转路径的目标跟踪

为验证在流场干扰下对沿回转路径运动的目标的跟踪性能，设定被跟踪船的期望路径为圆心(30,30)m，半径20 m的顺时针方向的圆弧，被跟踪船的初始位置为(13,10)m，跟踪船的初始位置为(13,5)m，结合实际河道宽度，设定抛物线型流场宽度为40 m，流向0°。仿真实验将对比分析不同峰速下跟踪船的跟踪误差，如图6所示。

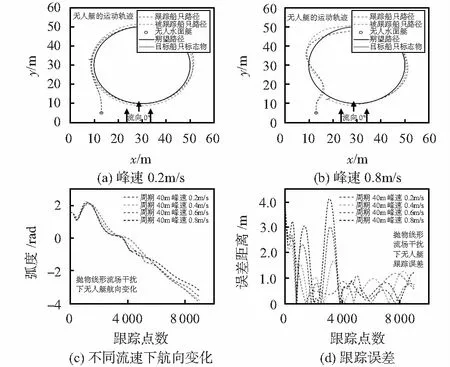
图6 流场干扰下回转路径的目标跟踪

仿真结果可以看出，随着流速的增大，跟踪船与被跟踪船的运动轨迹偏离期望路径的程度增大，航向变化也逐渐增大，导致跟踪误差也逐渐增大。基于固定双桨无舵的船体模型，仿真试验得出跟踪船能抵抗非均匀流场的最大流速为0.8 m/s。为了抵御流场的干扰，被跟踪船的实际航向与期望路径方向有一定的角度，但被跟踪船的速度和干扰的合速度仍指向期望路径，跟踪船正是利用这一部分合速度来平衡流场的干扰，当干扰的速度过大时，这一合速度将变小，导致被跟踪船无法前进。实验结果表明:在0.8 m/s的流速干扰以内，跟踪误差与航向误差随着流速的减小而逐渐减小，均保持在可跟踪范围之内。

4 结束语

本文针对无人水面艇跟踪水面目标物的问题提出一种基于单目视觉的无人水面艇目标跟踪方法。为验证本文提出视觉跟踪算法的有效性，仿真实验设定不同峰速的流场干扰、不同期望路径对跟踪精度的影响进行分析。实验结果表明:不同峰速的流场干扰下，峰速越大，跟踪误差和航向误差越大，反之越小。针对本文所述“海翔号”船体模型可以得出，流场峰速在0.8 m/s以内，本文算法能够保持良好的跟踪效果，为下一步的实际实验奠定了理论基础。