“一棵大树”立模型,助解题,促发展
江苏省苏州市工业园区星汇学校(215127) 田 潇
数学模型是特定类型的题目可以概括为一种思想方法来解决问题,归纳数学模型可以帮助学生在解题中高效的,高质量的解决问题,不仅能提高学生的学习效率,还能提高学生对问题认识的深度和知识理解的系统性.本文是依据学生在利用勾股定理解决问题过程中出现解题困难、思考不到位,不能够灵活运用知识解决此类问题的现象.针对此问题,笔者为了让学生加强理解,从题目中总结规律,建立模型,再运用这模型去解决共性问题,所以便于学生理解和掌握,笔者给这类型的题目总结了一个模型“一棵大树”,这样贴近学生的最近发展区,来源于生活的额模型有助于学生理解和自主构建知识体系,从而能够灵活运用模型高效解题,巩固所学内容,提升自己的思维能力.
1 定理再现,追本溯源
勾股定理:直角三角形两直角边的平方和等于斜边的平方.如图,∵∠C=90°,∴a2+b2=c2.

勾股定理是学生在已经掌握了直角三角形的有关性质的基础上进行学习的,它是直角三角形的重要性质,它把三角形有一个直角“形”的特点转化为三边之间的“数”的关系,它是数形结合的典范.定理的作用是已知直角三角形的两边,求第三边.利用好这个关系它可以解决许多直角三角形中的计算和应用问题.提出定理是能够在解题中帮助学生再次把握和理解模型的基本条件和存在模式,揭示模型产生的根源,符合学生的认知心理,从而为利用模型解决问题做好铺垫.
2 经典例题,提炼模型
(1)如第1题图一棵大树在其三分之一的D处折断,量得AC=5米,则旗杆原来的高度为____.
(2)已知,如第2题图,长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕为EF,则ΔABE的面积为( )
A.6 B.8 C.10 D.12

第1题

第2题
分析第一题中已知CD=1/2AD,AC=5.第二题已知条件需要利用翻折的性质去挖掘隐藏的条件,通过翻折其实已知条件是AE+ED=AD=9,AB=3.二个典型例题存现出的条件都是相仿的,已知两边固定关系,第三边具体长度,通过构造或已知所在的直角三角形,从而利用勾股定理解决问题.
两个例题从基本题型出发,利用典型题目启发引导学生自主探索,自主研究,教师启发引导,分析隐形条件,思考解决问题办法,找到共性思路,为提出模型做好铺垫.分析典例条件引导学生思考,已知两边关系和一边具体的值,要求第三边,需要找到或构建直角三角形,利用勾股定理解决问题的基本思路,基本模型思想.因而根据此典型题目提炼出模型思路:在直角三角形中,已知一变量,另外两边之间存在着一定的关系即已知a=x,c+b=y,利用a2+b2=c2解决问题,把直角“形”的特点转化为三边之间的“数”的关系来解决问题.这样我们就可以设一边来表达与之相关的另一边,从而利用勾股定理解决问题,初步形成了找到这类问题的共性方法“一棵大树”模型.模型的提炼是重在启发和引导学生利用好条件,根据提炼出的模型完善所学知识,灵活运用模型,从而高效的解决问题.
3 变式练习,巩固模型
(3)已知矩形ABCD沿直线BD折叠,使点C落在同一平面内C′处,BC′与AD交于点E,AD=8,AB=4,求DE的长.
分析已知C′D=4,通过翻折,利用矩形的性质,发现ΔABEΔC′DE,得出AE+CD=AD=8.通过对已知条件和隐含条件的进一步的分析,我们发现题目的解决方法最终回归到“一棵大树”模型的思路中.
(4)四边形ABCD是一张矩形纸片,AB=6,AD=8,在AB上取一点E,将纸片沿DE翻折,使点A落在BD上的点F处,则AE的长为______.

分析本题需要二次变换,通过翻转得到ΔADEΔEDF,得出BE+EF=AB=6,再利用矩形的性质和勾股定理已知量BF=2,这样又可以转换成“一棵大树”模型.
(5)如图,铁路上A、B两站(视为直线上两点)相距25千米,C、D为两个村庄(视为两个点),DA⊥AB于A,CB⊥AB于B,DA=15千米,CB=10千米,现要在铁路上建设一个土特产收购站E,使得C、D两村到E的的距离相等,则E应建在距A多少千米处?

分析根据AD=15,CB=10,AE+EB=AB=10,DE=CE条件,可借助两个直角三角形来解决问题,从而把“两棵大树”模型通过设而不解转化为“一棵大树”模型.
通过变式练习,对模型的基本条件重新构建,让学生在变式中感知,体验,总结提炼出模型的变换思路,在变式练习渗透模型思想,完善知识体系,让模型更具有活力.从复杂的图形中提炼出模型的基本图形,基本思路,让学生对模型有个更加深刻的认识,加深了对模型的理解,从而抓住模型的本质,灵活运用,举一反三,从总结知识到模型提炼,自主构建知识体系,三维角度提升学生解题能力,思维能力和创新意识.
4 自主构建,提升模型

(6)如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,请问水深多少?
分析通过条件,我们知道红莲在吹动到齐及水面时本身长度不变,根据右图可知,AC=6,AB=BC+3,这样我们就可以转化成“一棵大树”模型,自主构建直角三角形解决问题.
(7)如图,在RtΔABC中,∠C=90°,AC=3,BC=4.现将线段AC沿AD折叠后,使点C落在AB上,求折痕AD长度.

分析作出辅助线DH,利用折叠HE和勾股定理,得得出DH+DB=BC=4,BH=2,进而转换成“一棵大树”模型.
分析给定具体的一边长和另外两边的数量关系.
分析给定一边长,另两边长不固定,放大两边的数量关系,发散学生的思维,提升模型的利用率,多角度,多思维,多方向的解决问题.
分析进一步发散思维,提升对模型的思考维度,升华对模型的理解,从特殊到一般,由具体的边长变为不确定的边长,但模型思想的运用本质并不改变,从而强化了模型的存在性和合理性.
通过对实际问题的构建转换,使得模型更加具有说服性和传承性,更让学生通过自主构建条件,从外化模型到内化思维提升,从固定模式到自主构建,从模仿解决到自我发展,把知识的运用和解决升华到自我构建,自我完善,为今后学习夯实了基础,提供了自我创新和发展的提供了基本思路,也为思维的提升和解决问题的能力发展找到了方向.
5 实际运用,深化模型
(9)阅读:如图1,在直角ΔABC中,∠C=90°,AC,BC为直角边,AB为斜边,设BC=a,AC=b,AB=c,则a2+b2=c2.
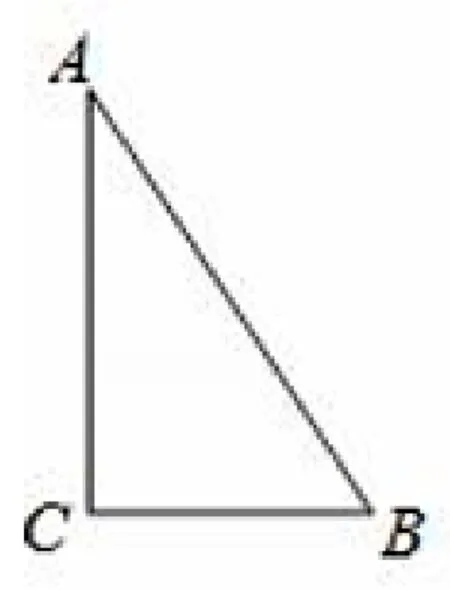
图1
例如,AC=8,BC=6,则可得10.根据阅读材料,完成题目:
如图2有一块直角三角形的绿地,量得两条直角边长分别为6cm,8cm.现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.

图2
分析建模型,用模型都是为了更好的解决生活问题.本题给定一个具体的直角边长,利用模型分类思考,自主构建解决问题的框架.
在教学中,教师要关注解题的方法,思路的提炼和总结,加强数学解题方法的延伸和升华,启发和引导学生对定理概念的再造和完善,从而在解题中培养学生分析问题,提出问题,解决问题的能力.
教学反思模型是解决问题的一种思路,帮助学生能够在共性问题中找到一种规律,帮助学生高效的解决问题.在教学中我们应该更多的关注学生自主构建知识体系,从学生的学习最近发展区出发,关注学生的思考过程,给学生思考的时间和空间,让学生在解题中总结归纳知识,主动自主的构建知识体系,发展学生的数学素养,在今后的解题中能够逐渐养成运用模型思想和数学的思维方式进行思考问题解决问题,不断增强发现问题,提出问题,解决问题的能力.
课堂教学要依托一定的模型思想,培养学生的良好解题习惯,增强数学思维的理解,让学生在解题中自主提升,在解题汇总完善所学知识,在解题中锻炼解题能力,在解题中提升数学思维.
用模型是为了更好的提高解题的效率,当然在用模型中怎样做到不拘泥模型的束缚,需要我们老师在选题和启发引导方面要根据模型的规律,注重学生对模型的知识的理解,对模型产生过程的探究,提高学生的解题技能和技巧,平时教学中注重能力和创新思维的培养,促进学生多角度,多思维的思考,不受模型的约束,又能借助模型产生过程和思想提升学生的总结能力和再造能力.模型只是一种解决共性问题的思路,我们关注更多的是学生自我能力的发展和数学素养的培养,这样,学生在今后的解题中,能够灵活运用自己所学的知识,所构建的知识体系来解决问题,提炼深化,不在畏惧难题,具备了一套自己解决问题的“通解”模型.

