黏度时变双液浆盾构壁后注浆过程数值模拟研究
李文广,王东武,张晨光,陈敬轩,曹宏涛
(1.中铁十八局集团第五工程有限公司,天津 300450;2.浙江工业大学 土木工程学院,浙江 杭州 310023)
盾尾壁后注浆工作多数基于工程经验,缺乏科学、合理的理论指导,导致注浆工程施工效果难以把控,盾构隧道变形[1-2]、破损[3]和渗漏等工程问题频频发生,维修成本高昂[4]。因此,深入探究各类注浆施工参数与注浆扩散形态的关系极具工程指导意义。目前,相关学者在盾构壁后注浆浆液填充扩散机理方面做了一定的研究工作。白云等[5]以单位时间内形成的盾尾空隙为浆液充填的横断面,推导出盾尾空隙横断面内浆液压力分布模型;李志明等[6]进一步将盾构同步注浆的填充分解为环向填充和纵向填充两个独立的阶段,没有考虑浆液纵横向扩散的相互影响,得到了环向填充及纵向填充的力学模型及计算方法;李培楠等[7]则建立了盾尾同步注浆纵环向整体扩散理论模型;胡长明等[8]基于简化假设条件分析了盾尾环向流体微元空间力学特性,建立了浆液在盾尾空间中的二元流环形填充扩散模型;苟长飞[9]建立了单液浆同步注浆时的扇形充填扩散模型;陈少波[10]依托南京轨道交通L5项目,分别采用环向独立模型和整体填充扩散模型对浆液压力分布模式进行计算分析,证实了整体填充扩散模型的准确性优势。然而,目前相关学者对盾构注浆填充扩散的纵横向耦合扩散研究甚少,值得进一步探究。
就材料而言,盾构壁后注浆主要采用以下两种浆液:以水泥为主的单液型浆液和以水泥-水玻璃(C-S)为主的双液型浆液。单液浆虽然流动性能好,利于填充扩散,且原料便宜,但是其往往存在稀释离析或筛滤流失等问题。而C-S双液浆中水玻璃类浆液起到速凝作用,该浆液有着流失少、泵送时材料分离度小、短期和长期强度均比较大、体积收缩低以及凝结时间短等优势[11-12],被越来越多地应用于盾尾同步注浆施工。然而双液浆凝结时间快(黏度时变特性不可忽略),在壁后注浆往往留有未充填的空隙,不能保证100%填充,会影响盾构注浆施工安全。目前的注浆研究鲜有考虑双液浆黏度时变性对注浆填充的影响[13]。因此,笔者深入探讨双液浆黏度时变性和施工参数对浆液纵横向耦合扩散的影响。基于多物理场耦合有限元软件COMSOL,模拟双液浆在盾尾间隙的三维局部填充扩散过程。通过控制变量,系统分析了浆液黏度时变性、入口注浆压力和注浆孔位置对注浆填充扩散特征的影响,以期为注浆工程采取合理的注浆策略提供参考。
1 有限元模型创建
COMSOL软件应用于非牛顿流体流动的模拟运算已经相对成熟[14-16]。刘人太等[14]针对水泥-水玻璃浆液与高聚物改性水泥浆液,应用COMSOL建立动水条件下裂隙注浆扩散的数值模型,研究动水条件下裂隙注浆扩散规律,分析不同黏度时变性、初始动水流速与注浆速率对注浆扩散的影响,并将数值模拟结果与模型试验进行对比,验证了数值模拟方法的有效性;高芙蓉[15]以脲醛树脂浆液为研究对象,在COMSOL中还原了室内注浆模拟中浆液的黏度时变性,并研究了浆液在含水砂层中的扩散机制,验证了脲醛树脂浆液对流砂的治理效果;杨志全等[16]依托COMSOL平台,通过二次开发得到考虑多孔介质迂回曲折效应的幂律流体渗透注浆的模拟程序,并以此开展不同水灰比水泥浆液在砾石土体中渗透注浆过程的数值模拟。
笔者基于浆液和空气两相流体的相互关系,且考虑两流体在扩散全程均为层流状态,将COMSOL流体力学模块中的层流物理场与两相流物理场进行耦合,对不同工况的盾尾同步注浆进行数值模拟计算,两相的界面追踪计算采用相场方法,对浆液的空隙填充过程进行数值模拟,浆液和空气在整个计算区域内的分布采用体积分数法进行表征。
1.1 物理场控制方程
1.1.1 层流接口的控制方程
模型基于Navier-Stokes方程模拟流体的质量和动量传递,为了考虑表面张力的影响,在控制方程中包含表面张力项,因此采用的Navier-Stokes方程为

(1)
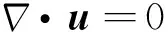
(2)

1.1.2 相场接口的控制方程
在相场接口中,两相流动力学由Cahn-Hilliard方程控制。该方程用于跟踪不相溶的两种液体的扩散界面。扩散界面定义为无量纲相场变量φ从-1到1的区域。在COMSOL中求解时,Cahn-Hilliard方程分成两个方程,即
(3)
(4)
式中:u为流体速度矢量,m/s;λ为混合能量密度,N;ε为界面厚度参数,m;γ为迁移率,(m3·s)/kg;ψ为相场助变量。
在相场接口中,各种流体的体积分数为
(5)
(6)
式中:Vf1为流体1的体积分数;Vf2为流体2的体积分数;φ为无量纲相场变量。
在笔者模型中,空气定义为流体1,浆液定义为流体2。后处理时,以两相体积分数各为0.5的等值面为相界面,追踪浆液的实时扩散面。
1.1.3 多物理场的耦合方程
多物理场耦合特征通过以下表达式定义混合物跨两相界面平滑变化的密度和黏度,分别为
ρ=ρ2+(ρ1-ρ2)Vf1
(7)
μ=μ2+(μ1-μ2)Vf1
(8)
式中:μ为流体黏度,Pa·s;下角标1,2分别表示流体1和流体2;其他符号含义同上。
1.2 几何创建、边界条件及基本参数
参考杭州下沙隧道工程盾构施工段的相关参数,构建局部注浆模型。基于化曲为直的简化思想,将弧形的局部盾尾间隙创建为7 000 mm×2 000 mm×200 mm的长方体空腔,并在前侧面的居中位置设定直径为80 mm的同步注浆管口,长方体空腔的两侧设为无压出流边界。其他壁面则设为无滑移壁(图1)。采用自由四面体网格进行划分,网格划分示意图见图2。

图1 三维几何建模Fig.1 Three-dimensional geometric modeling
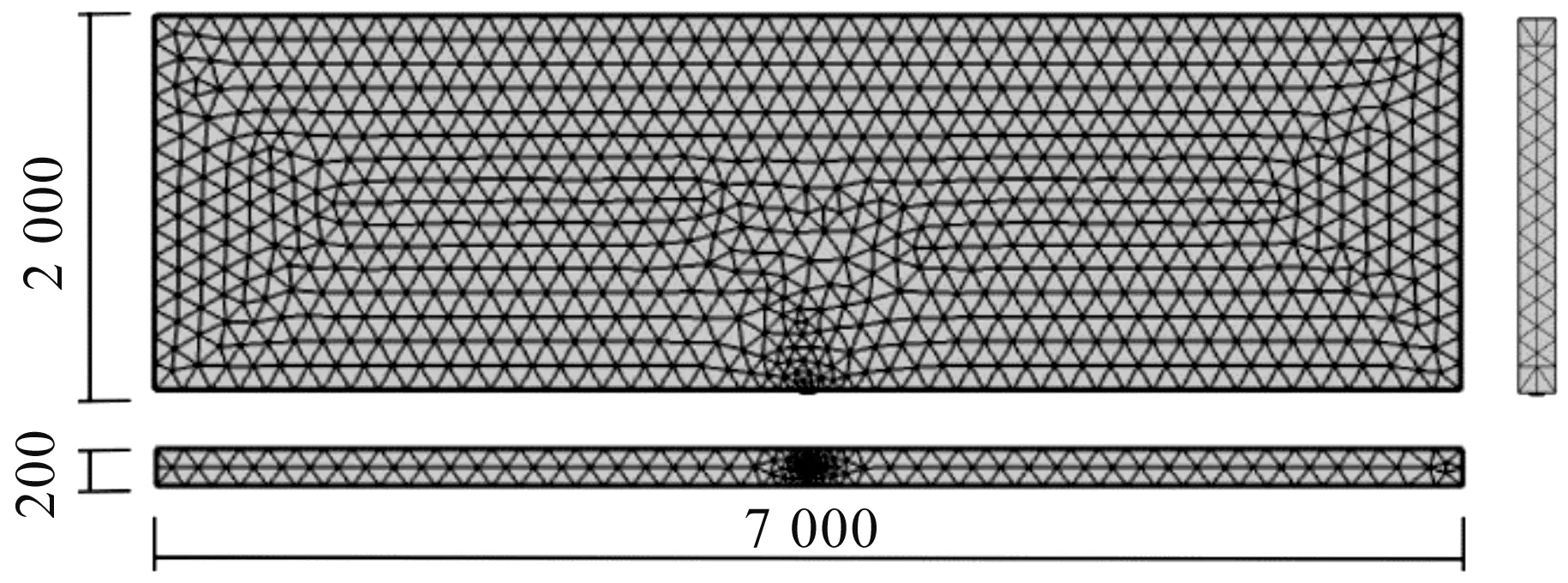
图2 网格划分(单位:mm)Fig.2 Mesh division (unit: mm)
模型计算初始状态设定局部盾尾间隙内填充相为空气,而注浆管道内的初始填充相为浆液,因此初始的两相界面位于注浆管体与待填充腔体的衔接面上。在恒定注浆入口压力条件下,浆液逐渐扩散并填充盾尾间隙,完成局部间隙的填充。
创建如图3所示的3条观测压力场与速度场的观测线,所有观测线均处在盾尾间隙水平对称面上。其中,观测线1通过注浆孔圆心且平行于侧面出口;观测线2平行于盾尾间隙前侧壁面且与其相距100 mm;观测线3平行于右侧出口且与其相距100 mm。观测线1将表征注浆入口正前方浆液注入方向的压力场分布与速度场分布;观测线2将表征与注浆方向垂直的横向压力场分布与速度场分布;观测线3的观测结果则反映了出口边界附近的压力场与速度场的分布情况。
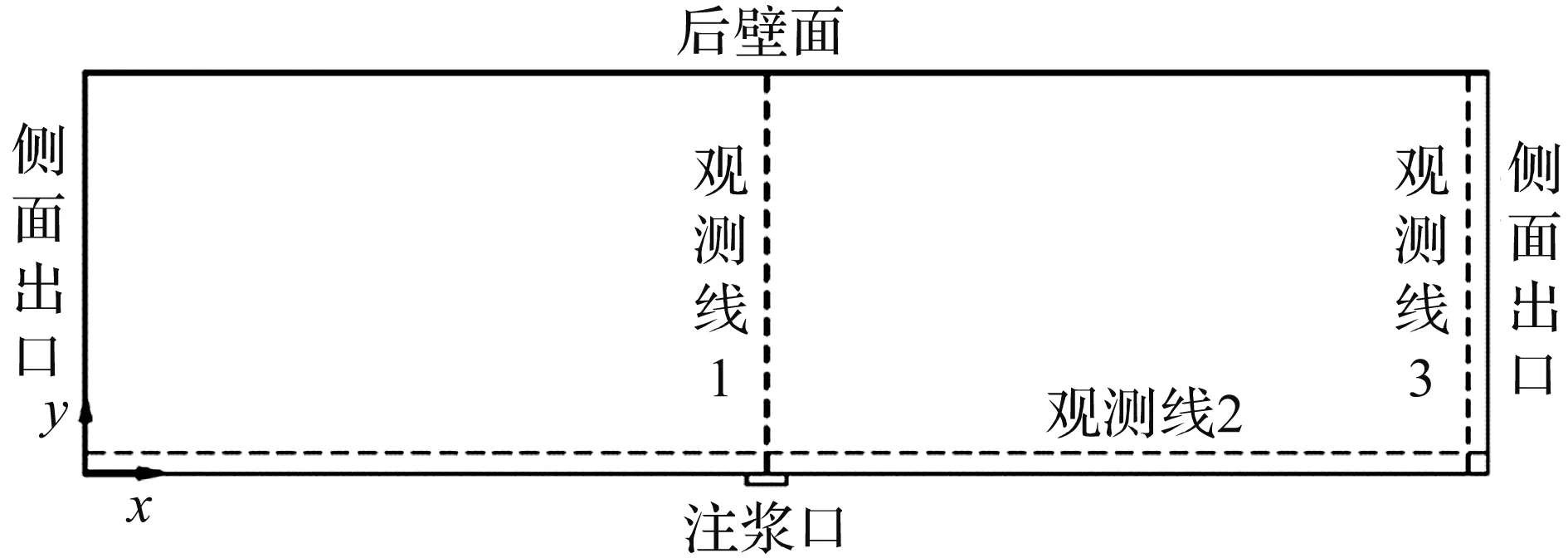
图3 观测线布置Fig.3 Observation wire cloth
1.3 计算工况
为研究浆液黏度时变性、入口注浆压力以及注浆孔位置对局部填充注浆的影响,共设定6种计算工况以供后期对比分析。考虑到浆液在配制完成后还需一段时间从调配位置运输到盾尾[17],设其黏度μ=0.018 64(t+50)2.066,单位为Pa·s;工况1,2,3采用不同的入口注浆压力,分别为100,200,300 kPa;工况1,5,6将盾尾间隙局部模型与重力的夹角设定为90°,60°,30°,从而模拟不同位置注浆孔的浆液扩散特征;工况4不考虑浆液的黏度时变性,认为浆液黏度值始终为t=0 s时的黏度值60 Pa·s,将其作为工况1的对照组,探究浆液黏度时变性对填充扩散的影响。综合以上各类参数的设定,通过控制变量的研究方法得出不同因素对浆液填充的影响。

表1 算例参数Table 1 Example parameter setting
2 浆液扩散典型工况分析
2.1 浆液扩散形态分析
当盾尾间隙局部模型与重力的夹角为90°时,在不同浆液黏度及入口注浆压力条件下,浆液的扩散形态具有相似性。因此,选择典型的工况3进行浆液的扩散形态分析,取6个代表时刻的浆液体积分数剖面图反映浆液的整个扩散过程。图4为工况3浆液扩散形态图,黑色轮廓线代表两相的分界面,即浆液的扩散边界。由于注浆条件、几何尺寸及边界条件的对称性,浆液的扩散形态整体呈现出对称性。扩散初期,浆液自注浆入口开始以扇形形态逐渐扩散,当浆液扩散面抵触到后壁时,浆液扩散面开始分成左右对称的两个界面向两侧开口继续扩散,直至填充整个盾尾间隙,完成局部填充。
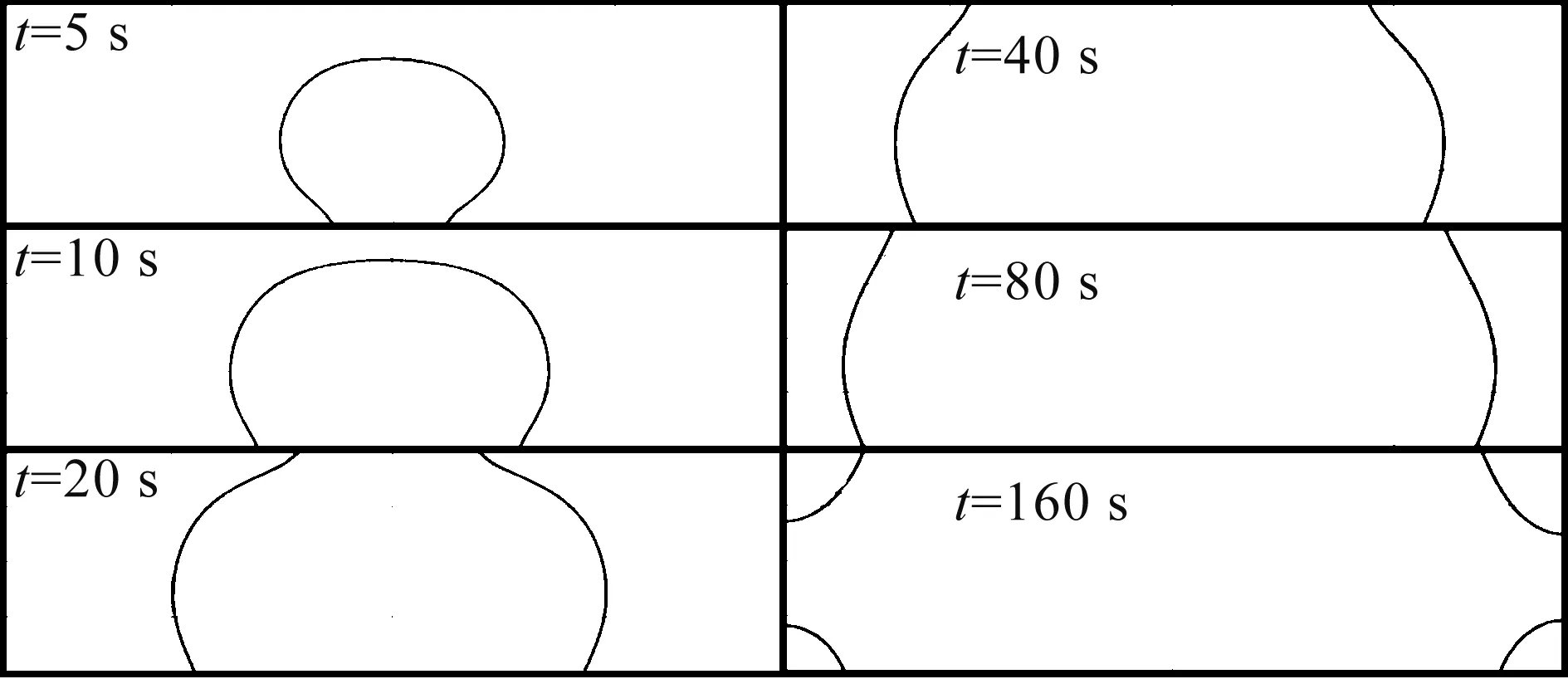
图4 浆液扩散形态(工况3)Fig.4 Slurry diffusion pattern (case 3)
2.2 速度场与压力场变化规律分析
2.2.1 速度场特性分析
以工况3测线上的速度场变化为例(图5),说明注浆过程中流体速度场随时间的发展规律。考虑到浆液的黏度时变性,即浆液黏度随时间推进不断增大。在入口压力恒定的条件下,入口处注浆流速随着时间推进锐减,观测线1与2中其他观测点的速度也随时间的推进而减小。此外,随着浆液扩散边界的发展,相同点后侧的浆液更为广泛,且黏度更大,从而提高了对该点的浆液推进阻力,这也是导致速度场值随着时间推进而逐渐减小的原因。观测线1与观测线2沿着y轴和x轴的速度场值分布基本相似,速度下降梯度在靠近注浆处最大,随着远离注浆口的位置逐渐减小。

图5 工况3速度场Fig.5 Velocity field of case 3
2.2.2 压力场特性分析
以工况3的3条测线上的压力分布为例(图6),说明注浆过程中压力场随时间的变化情况。由图6可知:观测线1与2的压力峰值均位于注浆口处,流体压力以注浆口为中心向四周递减。这是因为随着注浆范围增大,流体压力因内部剪切和边界摩擦沿程损失。考虑到浆液的黏度时变性,流速随着黏度增大而减小(图5)。根据流体力学中压力衰减与流速关系,流体流速越小,流体压降梯度越小[18]。因此,观测线1远离注浆口的压力值随时间推进略有提高。观测线2的压力值呈对称分布,流体压力随距离的变化规律和时间的推进规律与观测线1基本相同,即流体压力随着距注浆口距离的增大而不断减小。随着时间的推进,流速降低,因此沿程压力损失逐渐减小,远离注浆口的压力略有提高。在观测线2的两端,由于出流边界的压力始终为0,导致压力场最终均趋于0值。观测线3表征了沿着出口边界附近的压力分布规律。由于两侧出口附近的区域与注浆入口相距较远,且紧挨着出口边界,因此这些区域表征为相对均匀的气体低压场。通过对观测线3不同时刻压力场的对比分析,可以得出流体压力随时间的推进(即随浆液的扩展)而提高。在t=160 s时,由于浆液扩展到了观测线3的位置,在该时刻的局部区段压力(浆液压力)明显增大。
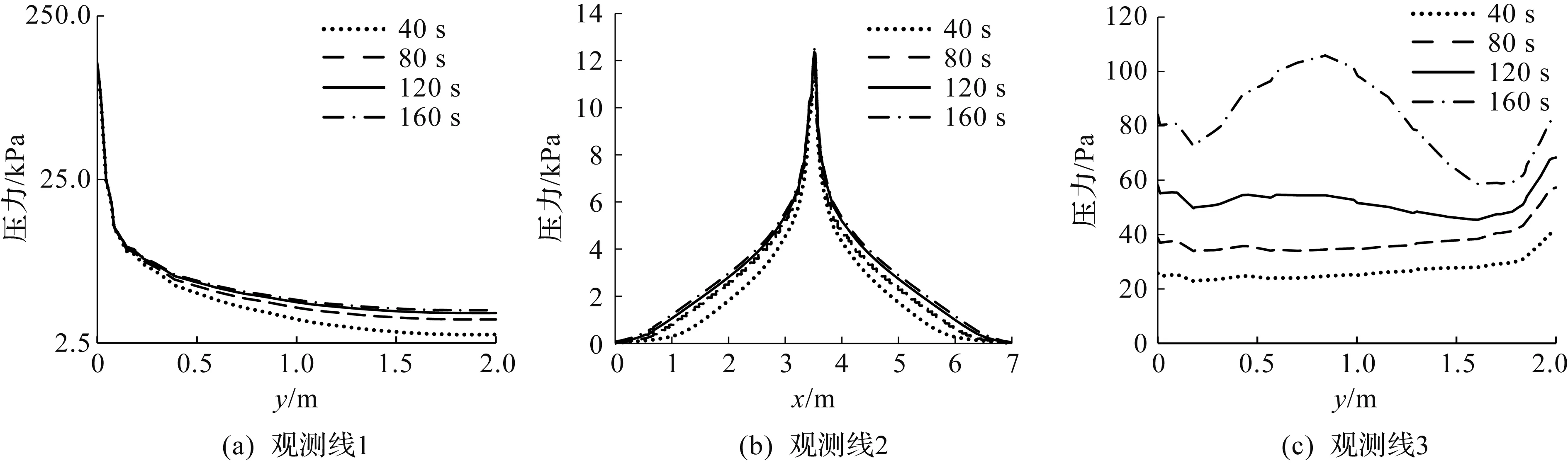
图6 工况3压力场Fig.6 Pressure field of case 3
3 不同参数对浆液扩散规律的影响
3.1 不同黏度模型浆液扩散规律
为研究双液浆黏度时变性对浆液扩散的影响,对工况1,4的模拟结果进行对比分析,结果如图7所示。在整个填充扩散过程中,相同时刻下不考虑浆液黏度时变性的浆液扩散面始终比考虑浆液黏度时变性的浆液扩散面发展更为广泛。
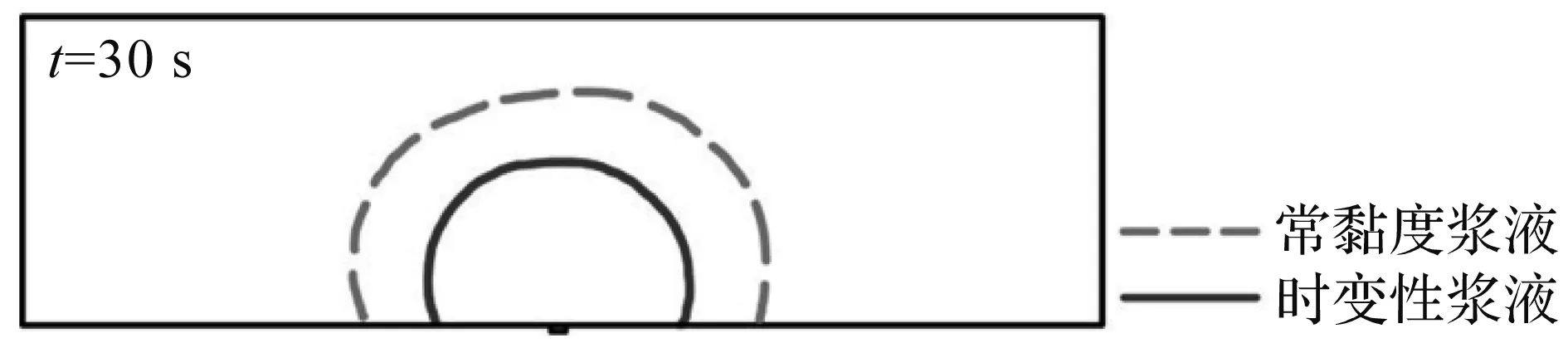
图7 工况1,4浆液扩散面(t=30 s)Fig.7 Slurry diffusion surface of case 1 and 4 (t=30 s)
进一步分析模拟结果中盾尾间隙观测线数据,探究黏度时变性对速度场和压力场的影响作用。工况1,4的观测线对应的速度分布如图8所示,压力
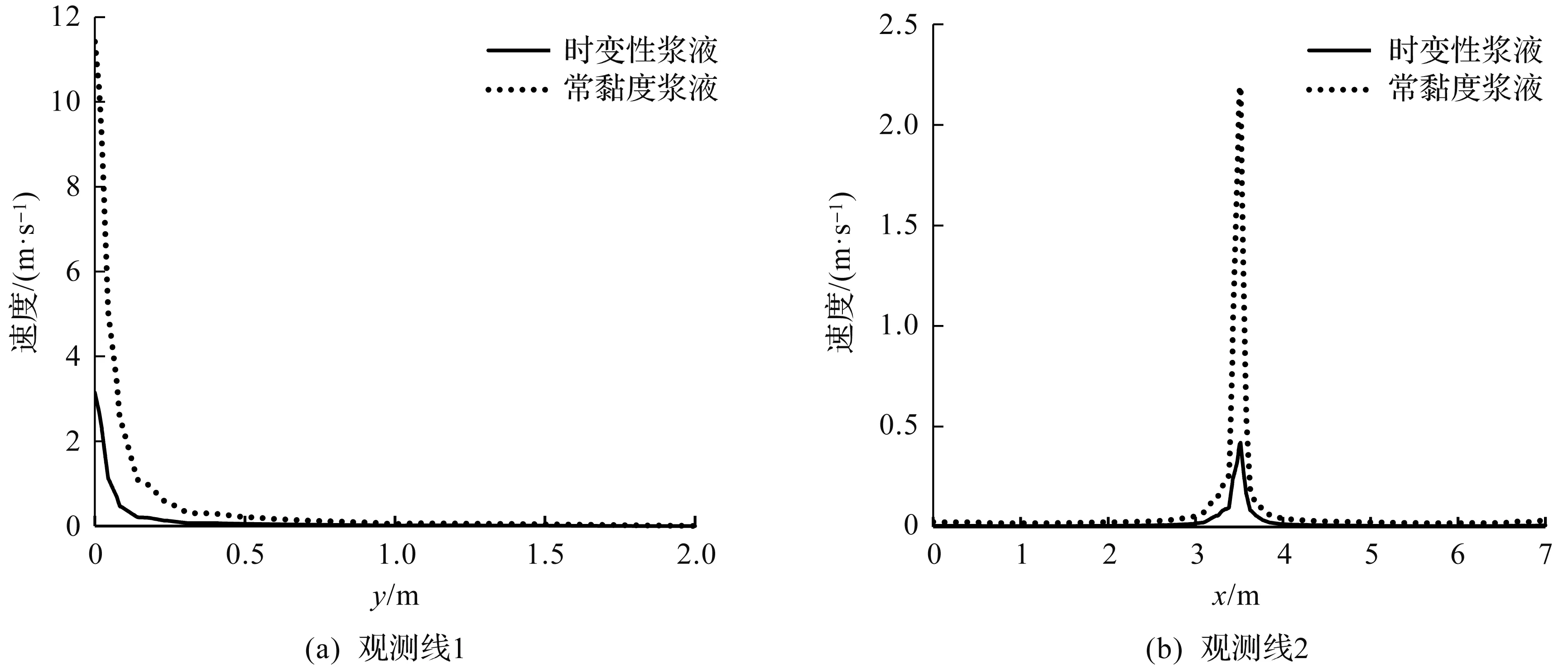
图8 工况1,4速度场(t=30 s)Fig.8 Velocity field of case 1 and 4 (t=30 s)
分布如图9所示。因为双液浆黏度的增加使得浆液流动过程中受到的摩擦阻力和内部剪切增大,造成流体动能在传递过程中的损耗提高,最终导致浆液压力场和速度场的减小[19]。因此,黏度与速度场、压力场呈负相关。在考虑浆液黏度时变性的工况中,随着时间推进浆液黏度增加,故在相同时刻下工况4的速度场与压力场比工况6的速度场与压力场更小。因此,在考虑浆液黏度时变性的工况中,浆液的整体扩散过程先快后慢。由此看来,双液浆的黏度时变性对浆液的填充扩散发展速度影响显著,在数值模拟和理论计算中均不可忽略。进一步对浆液扩散面在y轴方向上的推进距离d进行量化分析,结果如图10所示,经数据拟合得到工况1,4的d—t曲线的函数方程。考虑浆液为常黏度工况的d随t增长迅速;考虑浆液黏度时变性工况的浆液因黏度的不断提高,扩散阻力不断增大,使得d随t的发展由快转慢,这正是实际工程中注浆不充分的主要原因。
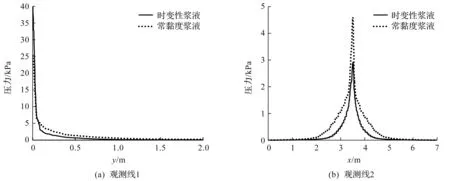
图9 工况1,4压力场(t=30 s)Fig.9 Pressure field of case 1 and 4 (t=30 s)

图10 工况1,4的扩散距离拟合曲线Fig.10 Diffusion distance fitting curve of case 1 and 4
3.2 不同入口注浆压力下的浆液扩散规律
如图11所示,对比入口注浆压力分别为100,200,300 kPa时浆液的填充扩散结果。通过对比分析可得:在相同时刻下,随着注浆压力的提高,浆液填充扩散发展越充分。
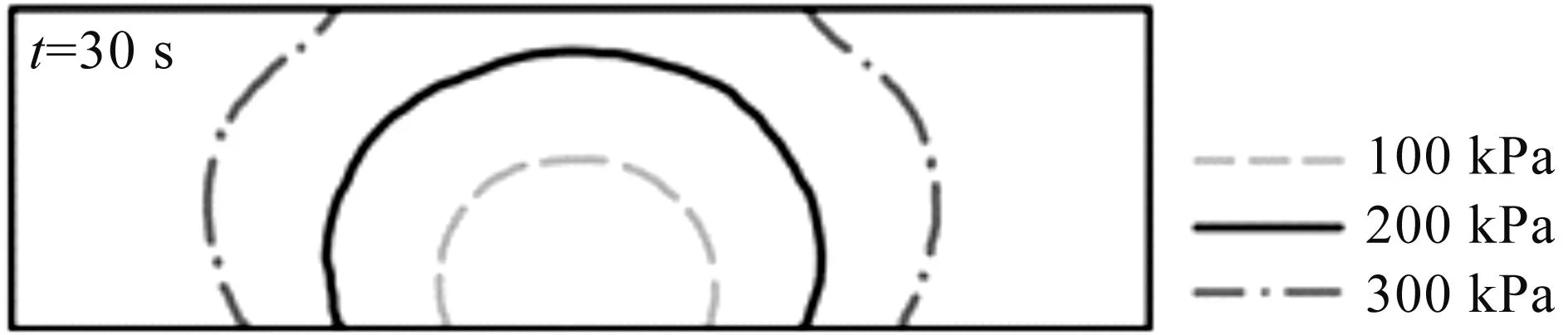
图11 工况1,2,3浆液扩散面(t=30 s)Fig.11 Dispersion surface of slurry in case 1, 2and 3 (t=30 s)
进一步分析浆液在填充盾尾间隙时速度场和压力场的不同,研究不同入口注浆压力对浆液扩散的影响。取工况1,2,3在t=30 s这一典型时刻的观测线数据进行分析,结果如图12,13所示。由图12,13可以得出:不同入口压力并不改变盾尾间隙内全局的速度场和压力场变化趋势,只是影响速度和压力的数值大小,且入口注浆压力与速度、压力均呈正相关。以观测线2为例,随着注浆压力的增大,观测线2的速度场随之提高,但速度场分布始终呈现对称的倒V型走势。注浆压力由100 kPa增至200 kPa,对应测线2上速度峰值增量为0.49 m/s。注浆压力由200 kPa增至300 kPa,对应测线2上速度峰值增量为0.57 m/s。随着注浆压力的增大,在相同的注浆压力增幅下,速度场增量略有提高。随着注浆压力的增大,观测线2的压力峰值分别为2 911,7 029,12 466 Pa。可见压力场与注浆压力也呈正相关,且随着注浆压力的增大,在相同的注浆压力增幅下,压力场增幅略有提高。通过对比分析所有观测线的压力场、速度场,可得入口注浆压力与研究域内的速度、压力均呈正相关。值得注意的是:由于工况1注浆压力较小,浆液发展相对较慢,在t=30 s时,盾尾间隙内仅在注浆口附近存在少量浆液,而观测线3距离注浆口较远且紧挨着零压出口边界,因此图13(c)的100 kPa的压力曲线表征为相对均匀的气体低压场。
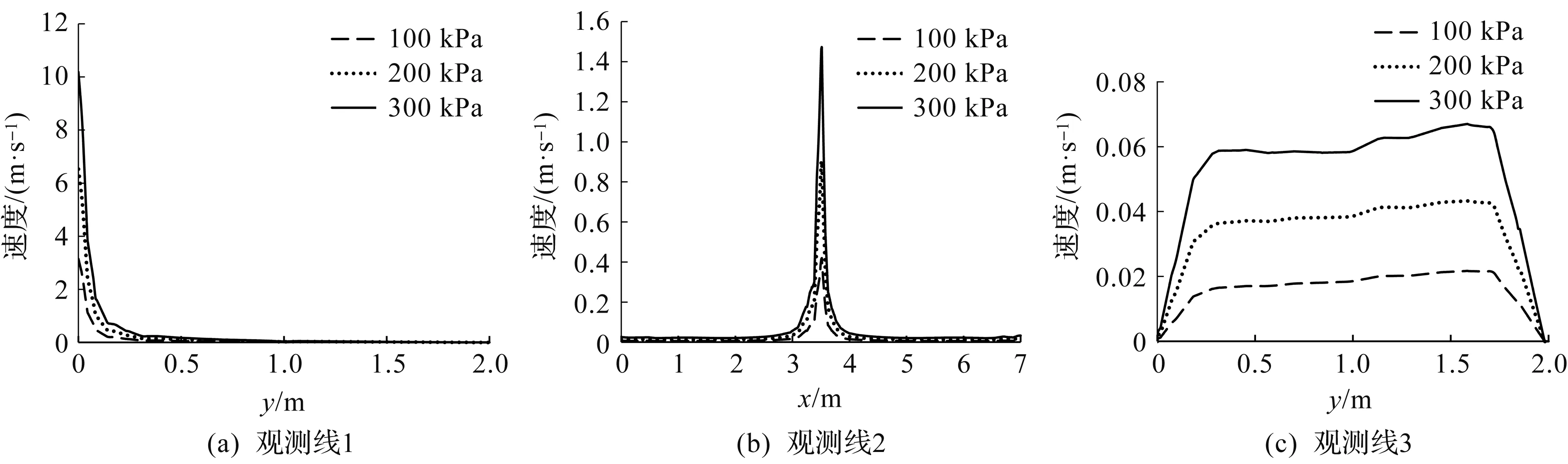
图12 工况1,2,3速度场(t=30 s)Fig.12 Velocity field of case 1, 2 and 3 (t=30 s)

图13 工况1,2,3压力场(t=30 s)Fig.13 Pressure field of case 1, 2 and 3 (t=30 s)
3.3 不同位置注浆孔浆液扩散规律
通过改变局部填充模型与重力的夹角,模拟不同位置注浆孔的局部填充扩散过程。当盾尾间隙局部模型与重力的夹角小于90°时,浆液扩散形态因重力作用体现出明显的不对称性,如图14所示,在工况6条件下,浆液右侧扩散面填充速度明显大于左侧扩散面。起初随着时间的推进,浆液迅速填充右侧盾尾间隙,随后浆液黏度的提高使得其可注性不断减小,浆体扩散面在注浆后期趋于稳定,因而左侧的空隙始终没有得到浆液填充,该模拟结果诠释了实际注浆工程中盾尾间隙填充不满工况的发展过程。
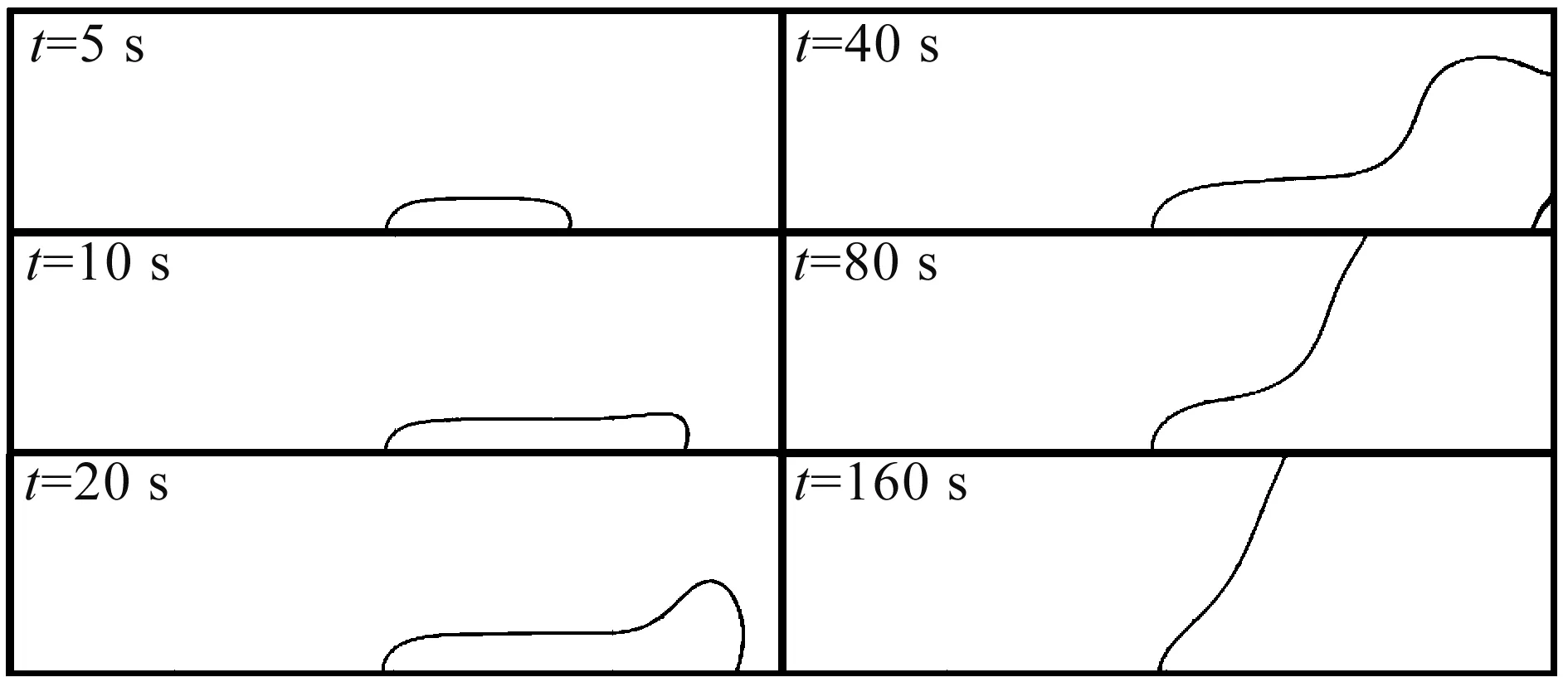
图14 浆液扩散形态(工况6)Fig.14 Slurry diffusion pattern (case 6)
如图15所示,对比不同重力夹角工况下模型内浆液扩散的发展形态可知:在相同时刻下,随着夹角的减小,浆液扩散形态的不对称性就越为明显。进一步观测模型内速度场和压力场的不同,探究不同位置注浆孔的浆液扩散规律,结果如图16,17所示。观测线2的速度场随着盾尾间隙与重力夹角的减小,速度数值出现左低右高的非对称性,且非对称性与重力夹角呈负相关。分析认为:随着重力夹角的减小,重力在盾尾间隙平面的分力随之增大,从而使得右侧浆液下滑,扩散加速发展;左侧浆液上爬,扩散减缓发展。由图17可以看出与速度场对应的压力场的不对称性也与夹角成负相关。该模拟结果说明:盾尾不同位置注浆孔呈现不同的浆液扩散形态,在实际施工时,应采取不同的控制参数。
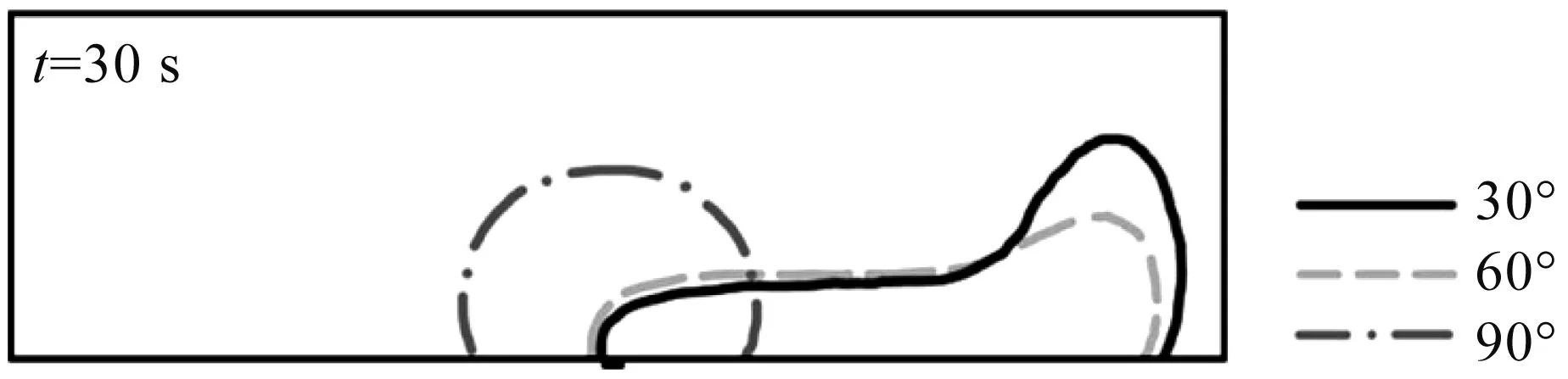
图15 工况1,5,6浆液扩散面(t=30 s)Fig.15 Dispersion surface of slurry in case 1, 5 and 6(t=30 s)

图16 工况1,5,6观测线2速度场(t=30 s)Fig.16 Velocity field of observation line 2 in case 1,5 and 6 (t=30 s)

图17 工况1,5,6观测线2压力场(t=30 s)Fig.17 Pressure field of observation line 2 in case 1,5 and 6 (t=30 s)
4 结 论
通过控制变量法,组合对比了不同工况下,盾尾壁后注浆局部模型内双液浆扩散面的发展过程以及速度场与压力场的变化规律,探究了盾尾壁后浆液的填充扩散机制,得出了以下结论:1) 浆液扩散速度与浆液的黏度呈负相关,而与入口注浆压力呈正相关;2) 由于双液浆具有黏度时变性,其扩散进程表现出显著的先快后慢的趋势,导致施工过程中盾尾间隙填充不满,因此在实际工程中应适当增加注浆压力,保证盾尾间隙填充率;3) 在盾构壁后注浆过程中,压力场和速度场的峰值出现在注浆口附近,且两者数值的大小基本都与注浆口距离呈负相关;4) 在盾尾不同位置的注浆孔中,顶部和底部注浆孔的浆液扩散形态基本对称,侧边注浆孔的浆液同时受压力和重力作用,扩散形态不对称,绝大多数浆液沿重力方向向下扩散并堆积,上侧区域填充不
满,因此在实际工程中可以适当增加顶部注浆孔的注浆量或上侧注浆孔的排布密度,以保证注浆效果。

