带有区间时变时滞的非线性扰动切换系统的指数镇定
冯改红,张志银,蔡国梁
(郑州升达经贸管理学院 应用数学研究所,河南 郑州 451191)
切换系统具有离散和连续的动态属性,是一类特殊的混杂系统。近年来,随着社会经济的发展和科学技术水平的提高,工业生产正面临机械化、智能化以及网络化的普及[1-3]。切换系统在日常生活中得到应用广泛,如空调调节温度、车辆变速箱档位变化、开关调节电灯亮度、人工智能学习策略转换和起重臂高度升降等。随着研究的深入,一些优秀的研究成果不断涌现[4-7]。时滞现象以及非线性扰动广泛存在于实际系统中,其存在使得系统的稳定性以及部分性能遭到严重的破坏,导致系统不能正常的运行,进而影响工业生产和日常生活。所以,带有时滞和扰动的系统在工程上有重要的应用。目前,针对切换系统的研究主要集中在系统稳定性、镇定、能控性等方面。随着众多科研工作者的不断参与,相应的研究结果已被提出[8-9]。然而,目前的研究仅仅考虑了常时滞和简单的时变时滞。事实上,由于区间时滞可能具有很大的时滞边界,相较于一般时滞,区间时滞对系统性能的影响最大。
笔者考虑了区间时变时滞以及非线性扰动对系统的影响,研究切换系统的指数镇定问题。首先,通过构建L-K泛函,引入自由参数,在证明过程中利用詹森不等式、索尔普引理以及平均驻留时间技术,得到了以矩阵不等式形式为基础的闭环系统指数镇定的充分条件;然后,通过矩阵适当变形,给出了控制器增益设计方法;最后,通过Matlab进行仿真,系统的状态轨线图说明了方法的有效性。
1 问题描述
建构切换系统,其表达式为

(1)
式中:u(t)∈Rm为控制输入;x(t)∈Rn为状态;φ(s)∈Rn为初始条件;Ai,A1i,Bi(i∈L)为常矩阵;σ(t)为切换信号,且σ(t):[0,∞]→L={1,2,…,n}为分段连续的函数,n为子系统的个数;{(t0,σ(t0)),(t1,σ(t1)),…,(tk,σ(tk)),…}为切换序列;t0为系统初始切换时刻;tk为系统第k次切换时刻。区间时滞函数d(t)满足
(2)
非线性扰动函数为f(t,x(t-d(t)))且满足
‖f(t,x(t-d(t)))‖≤‖Vi(x(t-d(t)))‖
式中Vi为已知常数矩阵。
对于切换系统式(1),使用如下形式的状态反馈控制,表达式为
u(t)=Kσ(t)x(t)
(3)
式中Ki(i∈L)为反馈增益矩阵。
(4)
定义1[10]记Nσ(t1,t2)为切换信号σ(t)在区间(t1,t2)上的切换次数,对于给定N0≥0,τa≥0,如果
Nσ(t1,t2)≤N0+(t2-t1)/τa
(5)
式中:τa为平均驻留时间;一般取N0=0。
定义2[11]闭环系统式(4)的平衡点x*=0在切换信号σ(·)和反馈控制u(t)=Kσ(t)x(t)下为指数镇定的,如果闭环系统式(4)的解满足如下条件:

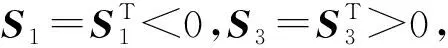

2 结果与讨论
以下给出闭环系统指数镇定的充分条件并进行证明。
定理1对于给定的正常数α和β≥1,如果存在正标量ε以及对称正定矩阵Pi,Qi,Ri,则对任意的i,j∈L(i≠j),成立矩阵不等式为
Pi≤βPj,Qi≤βQj,Ri≤βRj∀i,j∈L
(6)
(7)
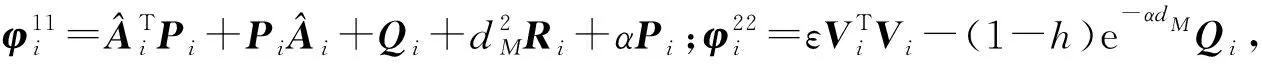
证明构建L-K泛函为
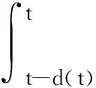
(8)
对系统轨线进行求导,可得
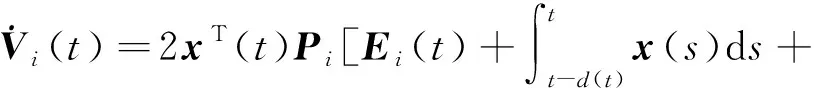
从而,可得

(9)
由于‖f(t,x(t-d(t)))‖≤‖Vi(x(t-d(t)))‖ε>0,则对ε>0有
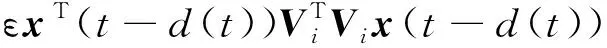
(10)
根据引理2可得到

(11)
由式(9~11)可得
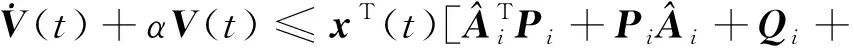
(12)
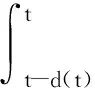

(13)
当t∈[tk,tk+1)时,对式(13)两端进行从tk到t的积分,可得
V(t)=Vσ(t)(t)≤e-α(t-tk)Vσ(tk)(tk)tk≤t (14) 由式(14)以及k=Nσ(t,t0)≤(t-t0)/τa,可得 V(t)≤e-α(t-tk)βVσ(tk-)(tk-)≤…≤ (15) 构建L-K泛函,可得 (16) 由式(15,16)可得 进一步简化为 由定义2可得闭环系统式(4)为指数镇定。 定理2对给定的正常数α和β≥1,如果存在正常数ε,矩阵Yi以及对称正定矩阵Xi,Ti,Oi,满足如下条件: Xj≤μXi,Tj≤μTi,Oj≤μOi∀i,j∈L,i≠j (17) (18) (19) 证明由于Ti>0,Oi>0,可得 (20) (21) 假设 (22) 由式(21)和引理1可以得到式(7)成立。根据定理1可知闭环系统式(4)是指数镇定的。 通过Matlab数值仿真计算来验证理论结果的正确性。针对系统式(1)考虑两个子系统,各系统参数分别为 通过式(17,18),可得 另外,可通过式(19)求得K1=[0.957 2 0.086 1],K2=[0.785 0 0.647 2]。 现假设系统初态为x(0)=[0.5 -0.5]T,利用Matlab仿真,可得闭环系统状态轨线,系统状态响应如图1所示。由图1可知:闭环系统在区间[0,12]前半段并不稳定,随着状态反馈控制器的作用,闭环系统逐渐趋于镇定,从而说明了该方法的有效性。 图1 系统状态响应Fig.1 State response of the system 首先,针对带有区间时变时滞和非线性扰动项的切换系统,根据Lyapunov稳定性定理,通过构建L-K泛函,研究系统的指数镇定问题;然后,针对区间时滞切换系统的镇定及控制器的设计,引入自由参数矩阵,利用自由权技术和平均驻留时间方法给出切换规律,建立以矩阵不等式为基础的非线性切换系统的指数镇定的充分条件,通过矩阵有规则的变形设计出该切换系统的控制器;最后,通过Matlab进行仿真,得到的数据和系统的状态轨线图说明了理论结果的有效性。带有区间时滞非线性切换系统的镇定问题研究具有积极的现实意义和一定的应用价值,后续,笔者会将其作为研究主题进一步开展深入研究。
e-α(t-t0)βkVσ(t0-)(t0-)≤
e-α-lnβ/τa(t-t0)Vσ(t0)(t0)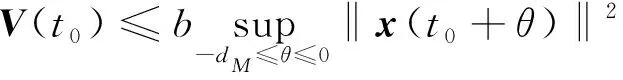
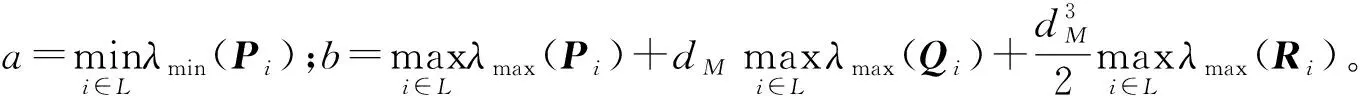
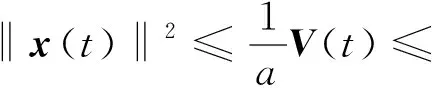
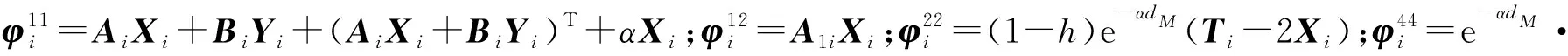

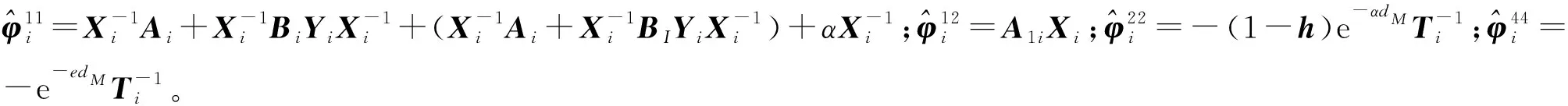
3 数值仿真
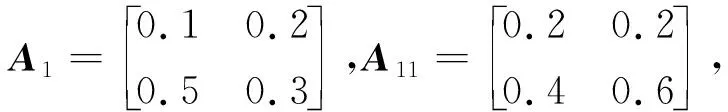
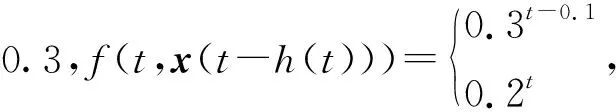


4 结 论

