考虑有效不透水下垫面的城市雨洪模拟模型
——Ⅰ.模型原理与模型构
周 宏,刘 俊,高 成,周 毅,胡尊乐,徐向阳,樊金璐
(1. 河海大学水文水资源学院,江苏 南京 210098;2. 河海大学水科学研究院,江苏 南京 211106;3. 江苏省水文水资源勘测局,江苏 南京 210029;4. 江苏省水文水资源勘测局常州分局,江苏 常州 213022)
作为全球最大的发展中国家,中国正处于城市化进程不断推进和深入的时期,常住人口城镇化率从1978年的17.92%增长到2019年的60.60%,城市建成区面积由1981年的7 438 km2增加到2019年的60 313 km2[1],平均每年增加约1 400 km2。快速城市化进程中不透水下垫面显著增加,改变了产汇流机制,导致城市内涝灾害频发[2]。雨洪模拟是有效应对城市内涝的一项关键支撑技术,对内涝防治及海绵城市建设具有指导意义[3]。
自爱尔兰人Mulvany于1850年最早提出推理公式,建立了一个由降雨强度推求相应径流峰值的简单“事件”模型开始[4],水文模型扮演着越来越重要的角色,发挥着越来越重要的作用。从20世纪70年代美国环境保护署(EPA)开发出SWMM(Storm Water Management Model)开始,城市雨洪模型不断发展,Salvadore等[5]罗列了40余种可用于城市雨洪模拟的水文模型,表明模型在城市雨洪模拟、管理、利用等方面发挥了重要作用[6]。然而,目前对城市雨洪模型中最重要的参数——不透水面积[7],缺乏深入研究。不透水面积包括有效不透水面积(Effective Impervious Area,EIA)、非有效不透水面积(Non-Effective Impervious Area,NEIA),EIA与NEIA之和为总不透水面积(Total Impervious Area,TIA)[8]。
目前国内外的主流城市雨洪模型的产汇流计算方法包括水文学方法和水动力学方法2类。几乎所有城市雨洪模型都包含下垫面不透水性的参数,但大多数模型并不区分EIA和NEIA。坡面产汇流过程为水动力学方法的模型,通过高精度网格考虑汇流路径,在汇流过程中区分了有效、非有效不透水下垫面的影响[9-10],但模型各模块之间耦合关系复杂,对资料要求高,在实际应用中受到限制。对于产汇流过程采用水文学方法的模型,早期通常的做法是直接使用TIA来表征汇水区的不透水性[11],也有模型使用EIA表征不透水性,但将NEIA直接当作透水下垫面(Pervious Area,PA)进行产汇流计算[12]。实际上,城市下垫面的异质性导致城市产汇流的复杂性。对EIA而言,其表面上的降雨除满足洼蓄、蒸发损失外几乎全部形成径流,并且产生的径流通过完全不透水的路径流动,直至到达雨水排放系统,EIA直接影响排水系统的径流过程;NEIA上产生的径流并不会直接进入排水系统,而是流至相邻的PA上,待到PA上也产生地表径流后排至管道或河道[13],即NEIA在与之相连的PA产生径流之前对地表径流过程没有影响[14]。因而,EIA和NEIA两者对流域出口过程线的贡献不同[15],上述2种常用的水文学方法均无法准确模拟城市雨洪过程。
近年来,作为应用最广泛的城市雨洪模型,SWMM考虑了EIA对产汇流过程的影响并作出了改进[16-17],可选择Outlet、Pervious、Impervious等不同出水口模式反映子汇水区内部汇流过程,但无法模拟不同子汇水区之间的水量交换。国内外也基于SWMM进行了二次开发[18-22],但多是与地表二维水动力模型耦合,或与数据管理及地图工具结合开发界面,而未对其产汇流计算方法进行改进。此外,海绵城市建设中,采取低影响开发(LID)措施往往加剧下垫面的异质性,导致子汇水区汇水范围、不透水性发生改变,各子汇水区内部及之间的汇流路径也可能产生变化。模型中往往难以直接反映这些变化,有时甚至需对模型重新概化,无法针对EIA的改变作出快速响应。
针对目前常用雨洪模型难以对EIA的改变作出快速响应的问题,本文有效区分EIA和NEIA等不同下垫面产汇流过程,研发考虑EIA的精细模拟模型,以适应新形势下雨洪管理实践的需求。
1 基于分类属性的EIA分步确定
为探究EIA的水文响应,基于下垫面分类信息,将不透水下垫面分为道路和屋顶,分别确定其EIA,主要分为空间数据获取及数字化、道路中EIA确定、屋顶中EIA确定3步,将屋顶从总不透水面积中分离出来,在道路EIA确定之后,利用城市雨洪模型及实测资料进一步率定屋顶EIA。
1.1 空间数据获取及数字化
空间数据获取是指借助ArcGIS将地理实体的空间数据和属性数据输入或转换为GIS数据的过程,将获取的高精度CAD数据转换为Shapefile、Geodatabase格式。空间数据可以包含丰富的点、线、面要素信息及其属性信息,目前数据多为CAD数据,尤其是排水管网信息。CAD数据在ArcGIS中是以组的形式存储的,主要分为Annotation(注记)、Point(点)、Polyline(线)、Polygon(面)等形式,使用ArcGIS的导出功能将CAD中的所有类型数据转换为Shapefile文件,主要包含高分辨率下垫面数据(面)、地表高程数据(点)、检查井数据(点)、排水管网信息(线)及河道资料(面),输出数据的类别、属性用各种不同的符号加以识别和表示。
1.2 道路EIA确定
道路中包含的EIA定量评估,主要是通过地表不透水下垫面排水路径来确定[23]。为了有效解决利用栅格数据在地形起伏较小的地区无法准确判断流动路径的问题,根据地形将实际高程接近的道路、建筑、绿地等划分成单个面要素,每个面要素中仅包含1种下垫面类型(如道路、屋顶、绿地、裸地),以面要素为分析对象,将Shapefile文件通过ArcGIS中的叠加分析,赋予每个面要素1个高程数据,然后借助ArcGIS确定每个面要素的流动路径,以面要素的流动路径来代替栅格确定流动路径,进而识别出EIA与NEIA。
(1) 面要素高程赋值。将数字化后输出的信息进行整合,尤其是对地表高程数据。由于数字化后的各种下垫面通常是作为1个面要素,其中往往包含较多个地表高程点,因而将数字化后空间数据中包含的面要素根据地形进一步分割,将同种类型下垫面中地表高程相近的区域分割为1个面要素,分割后的各个面要素内部高程点基本接近,通过ArcGIS的属性计算,将包含的高程点求平均值后赋值给面要素,作为该面要素的高程属性。
(2) 流向分析。流向分析主要是基于各个不透水下垫面面要素的高程信息,首先判断单个不透水面要素的流向,然后根据流向将所有面要素连接成汇流网络。流向的判断主要借鉴D8算法,假设单个面要素水流的流向有若干种可能(主要取决于包含几个相邻的面要素),但水流只能从1个方向流出,采用最陡坡度法来确定水流的方向,即计算目标面要素与各相邻面要素间的距离权落差,取距离权落差最大的面要素为目标面要素的流出方向[24]。当目标面要素与周边面要素具有相同的距离权落差时,该算法无法识别最陡的斜率,此时需人工判别该面要素的流动方向[15]。
(3) 汇流路径分析。首先,将检查井位置数字化为单独的GIS点状图层,并利用ArcGIS叠加分析功能,根据检查井位置信息对各面要素是否包含检查井进行赋值;其次,判别面要素自身是否包含检查井,如果面要素自身包含检查井,则该不透水下垫面直接划分为EIA;最后,根据流向分析方法确定不透水下垫面流动路径,在计算汇流路径过程中,如果识别到流入的面要素中包含检查井,则计算停止,包含检查井的面要素即为目标面要素汇流路径的终点。分析目标面要素的汇流路径,如果汇流路径中所有面要素均为不透水下垫面,则目标面要素为有效不透水下垫面;如果汇流路径中包含透水下垫面,则目标面要素为非有效不透水下垫面。
(4) EIA确定。根据汇流路径分析的结果,给不同道路面要素赋值为EIA或NEIA。对极少数目标面要素无法判别是否为EIA的情况,进行目视检查。例如,对于某些道路无法判定是排至雨水管网还是相邻的透水下垫面,可根据具有相似建设年限、相似地形、沿着街道具有相同排水基础设施的相邻下垫面的特征来推测该属性[23]。
1.3 屋顶EIA确定
对于屋顶部分EIA确定,理论上应按照落水管连接情况判断屋顶是否为EIA。比如,当所有落水管连接到雨水管网时,则屋顶被全部划分为EIA;当屋顶上的所有落水管连接到草坪或其他透水表面时,则屋顶被全部划分为NEIA;如果屋顶80%的落水管连接到排水系统,20%连接到草坪或其他透水表面,则80%的屋顶面积被划分为EIA,20%被划分为NEIA。
然而,由于现有地图和GIS数据通常不包括落水管位置及排水方向,因而无法获得屋顶的实际径流路径信息,即无法单纯通过地形资料和GIS数据识别并量化屋顶中包含的EIA。为了准确评估屋顶中的EIA比例,在城市雨洪模型中设置了参数γ(屋顶直接连接到排水系统的比例),即屋顶面积的γ部分为EIA,其余为NEIA,此参数作为率定参数在模型率定与验证过程中确定。
(1) 选择合适的实测资料。为了科学确定屋顶直接连接到排水系统的比例,消除模型率定过程中“异参同效”对确定γ的影响,要选择合适的实测资料。选择的实测降雨场次,应主要为有效不透水下垫面产流,透水下垫面尽量不产流或少产流,以消除下渗率调整对模型结果的影响。因而,应选择降雨量级较小,主要为不透水下垫面产流的降雨场次。
(2) 确定模型率定的目标函数。模型率定过程中如果满足以下条件则EIA的评价会比较接近真实值[8]:① 率定过程中目标函数对EIA的数值变化较敏感;② 模型中EIA的初始值与实际值较接近;③ 模型中其他参数与EIA相互作用较少,即模型的“异参同效”不明显。由于大部分城市地区的EIA小于TIA,即TIA中还会包括一部分NEIA,且城市中的透水下垫面也是径流来源重要组成部分,因此如果产流过程中不透水下垫面、透水下垫面上均产生径流,则峰值流量与径流总量不仅与不透水面积有关,还与透水下垫面的下渗速率有关,故较难区分屋顶直接连接到排水系统的比例与下渗速率的影响。
为了解决上述问题,在参数率定过程中考虑将EIA与下渗率分开率定。由于降雨量较小时径流基本为EIA上产生,而PA及NEIA上不产流,因而可采用降雨总量较小的降雨过程率定γ。对于下渗率,由于降雨量较大时,所有下垫面上均产流,当γ确定后,径流的产生主要取决于下渗率的大小,此时可采用降雨总量较大的降雨过程率定下渗率。
由于短时间内蒸发量较小,影响EIA产流的参数决定洪量的大小,主要包括不透水下垫面洼蓄量、γ;影响EIA汇流的参数仅会影响洪水的过程,并不会决定洪量大小,主要包括不透水下垫面的糙率、管道及河道的糙率。因而考虑将场次降雨径流过程的洪量作为模型率定的目标函数,需要率定的参数仅为不透水下垫面洼蓄量、γ。虽然不透水下垫面洼蓄量、γ两者均会直接影响洪量大小,但不透水下垫面洼蓄量变化范围较小(一般取值为1~2 mm),对洪量影响不大,根据经验即可确定,因而当选择洪量作为目标函数时,可以认为所需率定的参数仅包含γ这1个参数。所以,在确定屋顶直接连接到排水系统的比例这一参数时选择洪量作为目标函数。
(3) 确定γ及EIA。先赋予γ1个初值,利用构建的城市雨洪模型计算得到洪量,与实测降雨径流过程的洪量进行比较,并根据比较结果调整γ,直至与实测资料吻合较好为止,从而最终确定屋顶中的EIA。
2 考虑EIA的城市雨洪精细模拟模型构建
2.1 模型结构
城市下垫面的空间异质性,尤其是不透水下垫面的空间异质性,导致了城市产汇流过程与天然流域存在差别。总的来说,有不同类型的水文模型可用于模拟城市产汇流过程。虽然这些模型在所需输入、水文过程表示和计算输出的算法方面各不相同,模型的实用性也因集水区特征、数据可用性和用户目标而异[25],但无论何种模型,不透水性对城市水文响应都有重要影响。在确定城市集水区的水文响应时,需要准确评估下垫面的不渗透性[26],有效区分EIA和NEIA,揭示产汇流过程的差异,厘清二者对城市集水区产汇流的影响,以便更好地管理集水区内的城市开发、预测未来情景下的水文响应[27]。
为了达到这一要求,在模型构建过程中主要考虑空间离散程度、模型输出的不确定性、计算耗时三者之间的平衡[16],合理划分不同下垫面类型,将下垫面划分成透水和不透水两大类,不透水又细分成道路和屋顶2种,每种都包括EIA和NEIA,选择合适的空间离散方式与程度,并考虑EIA、NEIA、PA等下垫面空间异质性对汇流过程的影响。采用合理的产汇流方法,构建适用的城市雨洪精细模拟模型,对EIA、NEIA、PA等不同类型的子汇水区采用不同的产流计算方法,坡面汇流过程考虑子汇水区内的坡面汇流以及不同子汇水区之间的坡面汇流,再经过管网及河网汇流计算得到出流过程。
2.2 下垫面离散
集水区的特性决定了城市径流的数量和质量,在城市雨洪模拟过程中,如何将集水区下垫面离散并表示为空间要素对模型参数和模拟结果都有较大的影响[28]。因而,集水区细分并表示为空间要素在很大程度上决定了城市雨洪模型的输出[16],影响城市雨洪模拟的准确性。平衡下垫面离散程度、输出不确定性和计算耗时三者之间的关系[16],将具有高度异质性的城市下垫面离散成均匀或“准均匀”特性的子汇水区对城市雨洪模拟是十分重要的[28-29]。区分EIA和NEIA,下垫面的离散主要有图1中几种方式。
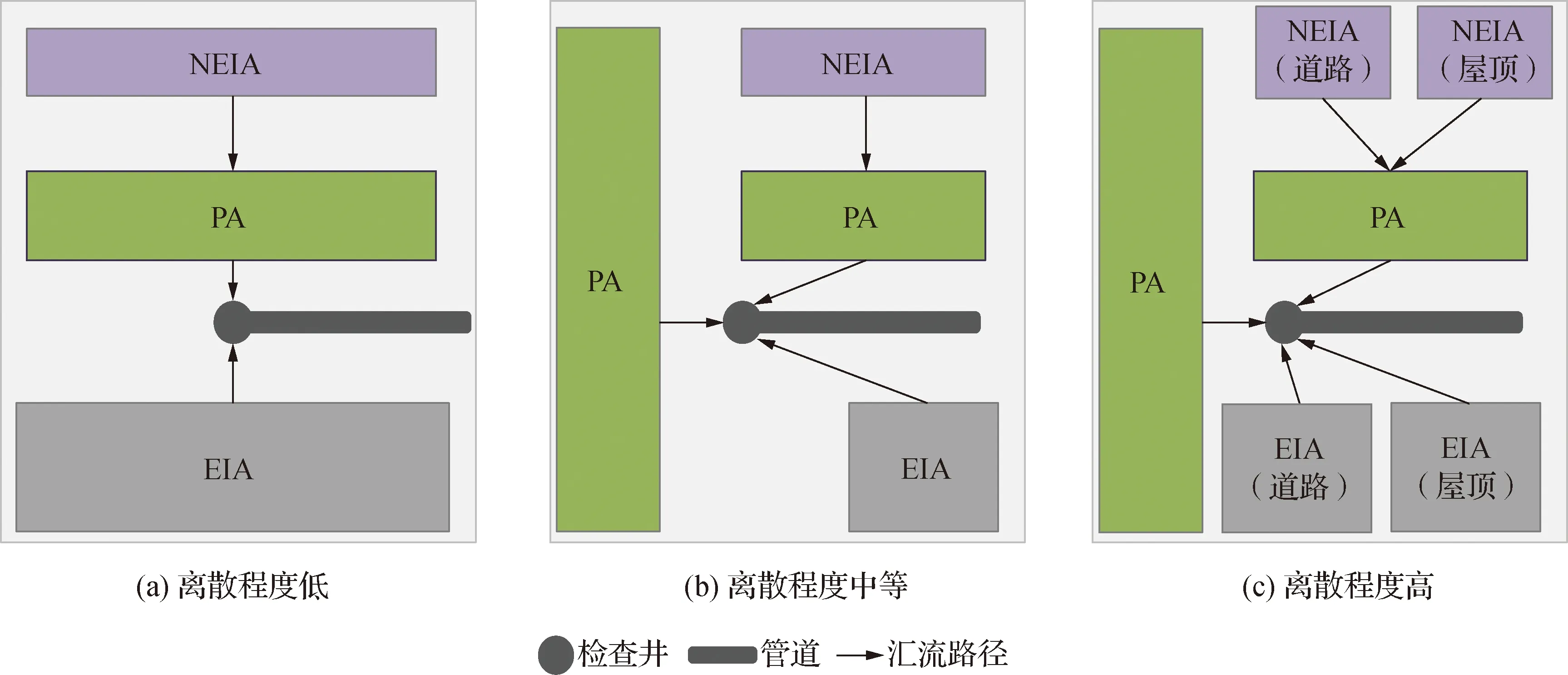
图1 下垫面不同离散程度示意Fig.1 Diagram of different degrees of dispersion of the underlying surface
下垫面离散程度最低的是图1(a),1个子汇水区,仅考虑EIA、NEIA和PA,EIA和PA直接进入排水系统,NEIA通过PA进入排水系统,整个区域被概化为3个集总的子汇水区,将所有的空间异质性集中到一个没有物理现实基础的虚构空间中[16],离散程度较低,模型输出不确定性较大,预测能力可能较差。下垫面离散程度最高的是图1(c),将每块不透水和透水下垫面离散为一个独立的子汇水区,并且不透水下垫面中区分道路和屋顶,还可表示不同子汇水区之间的汇流过程,这种精细的离散方式可以降低模型输出结果的不确定性[30],但需要确定所有子汇水区之间的流向以及为细分的每个子汇水区确定各自的参数。
无论城市实际的下垫面是多么不连贯,一个集水区内的所有下垫面都被离散概化成为一个个单独产汇流的子汇水区,这建立了子汇水区大小和模型空间分辨率之间的关系。子汇水区面积越大,所产生的空间聚集越强,下垫面异质性也就反映得越不充分,模型可能也就越脱离实际。下垫面的离散结果,包括子汇水区的大小、下垫面的异质性及其在每个子汇水区内或子汇水区之间的相互作用,将影响模型的复杂性和准确性。总的来说,下垫面离散程度较高且模型经过良好的率定、验证后,模型输出的不确定性将会降低[16],预测的准确性会得到加强;相反,下垫面离散程度较低,即使模型经过率定、验证后,模型预测的准确性不高,用于模拟其他地点,特别是无实测资料的地点时,结果的确定性也不高。
为了准确地表征城市下垫面异质性及地表汇流过程,排水区域应没有或很少有影响水文特性的景观特征的空间聚集。因此,综合考虑不同下垫面离散水平导致的模型输出不确定性和计算时间差异,模型离散方式选择图1(c),以较为准确地反映不同类型下垫面的产汇流过程,提高模型输出的准确性。
2.3 不同下垫面产流计算
2.3.1 有效不透水下垫面
在城市雨洪模拟过程中EIA上产生的径流,降雨损失仅考虑洼地蓄水,有效不透水下垫面产流强度(rEIA)为
rEIA=i+DIAi-DIA
(1)
式中:i为降雨强度,mm/min;DIAi为第i时段不透水下垫面洼蓄量,mm;DIA为不透水下垫面最大洼蓄量,mm。
洼蓄由于雨间地面蒸发而消耗,时段递减计算公式为
DIAi+1=DIAi-EIAi
(2)
式中:EIAi为第i时段不透水下垫面地面蒸发,可由水面蒸发(Ei)折算推求:
EIAi=βIAEi
(3)
如果有相邻的PA上的径流流动至该子汇水区, 则降雨强度应为
(4)
式中:βIA为折算系数;iEIA为有效不透水下垫面降雨强度,mm/min;rPA为流入该子汇水区的透水下垫面的产流强度,mm/min;SPA为透水下垫面子汇水区的面积,m2;SEIA为有效不透水下垫面子汇水区的面积,m2。
如果没有相邻的PA上的径流流动至该子汇水区,则降雨强度应为
i=iEIA
(5)
因此,在时段Δt内,地表产流深(hEIA)为
hEIA=rEIAΔt
(6)
此外,由于不透水下垫面中直接连接到下游收集系统的屋顶部分的值是在子汇水区和集水区尺度上准确估计EIA的一个重要参数,因此,在模型中将EIA主要分为道路和屋顶2类。由于屋顶是排至雨水系统还是排至建筑相邻的透水下垫面较难调查,故将屋顶直接连接到排水系统的比例作为率定参数在城市雨洪模拟过程中进行率定。
2.3.2 非有效不透水下垫面
NEIA将径流输送至相邻的透水下垫面,在透水下垫面产流之前不产生直接径流,与EIA的主要差别在于汇流过程不同,产流计算与EIA一样,非有效不透水下垫面产流强度(rNEIA)为
rNEIA=i+DIAi-DIA
(7)
如果有相邻的PA上的径流流动至该子汇水区,则降雨强度应为
(8)
式中:iNEIA为非有效不透水下垫面降雨强度,mm/min;SNEIA为非有效不透水下垫面子汇水区的面积,m2。
如果没有相邻的PA上的径流流动至该子汇水区,则降雨强度应为
i=iNEIA
(9)
在时段Δt内,地表产流深(hNEIA)为
hNEIA=rNEIAΔt
(10)
2.3.3 透水下垫面
雨降到地面后,首先满足植物截留、湿润地表土壤和填洼等损失,然后当雨强大于下渗率后产生地表径流(RS),渗入到土壤中包气带层的水被土壤吸收,当土壤含水量大于田间持水量时,出现自由水在土壤中流动,一部分流出地面称为浅层流或壤中流,另一部分继续下渗补充地下水,在城市中这2部分水在当次洪水中基本不流出。
透水面积的降雨损失包括雨期蒸发、植物截留、填洼和土壤蓄水。在下渗可及的包气带土壤含水量W=0时,其下渗率为最大下渗率(f0);在充分供水条件下,土壤含水量逐渐增加,相应下渗率(f)逐渐减小,当土壤缺水量全部蓄满即达到田间持水量(Wm)时,即W=Wm,相应的下渗率为稳定下渗率(fc)[31]。假定透水面积下渗率满足霍顿公式
f=f0exp(-kt)+fc[1-exp(-kt)]
(11)
式中:t为时间,min;k为与土壤特性有关的经验常数。
根据文献[12]中透水下垫面产流过程推导,不同降雨强度i rPAs=i-f[1-(1-i/Im)1+b]+DPAi-DPA (12) 当降雨强度i≥Im时地表径流产流强度为 rPAs=i-f+DPAi-DPA (13) 洼蓄由于雨间地面蒸发而消耗,时段递减计算公式为 DPAi+1=DPAi-EPAi (14) 式中:rPAs为透水下垫面地表径流产流强度,mm/min;Im为点最大下渗率,mm/min;DPAi为第i时段透水下垫面洼蓄量,mm;DPA为透水下垫面最大洼蓄量,mm;EPAi为第i时段透水下垫面地面蒸发,可由水面蒸发折算推求。 需要注意的是,式(12)及式(13)中的降雨强度可能还包括与之相邻的NEIA上流至该子汇水区的产流强度(rNEIA),故当有NEIA汇入透水下垫面时,透水下垫面上降雨强度可表示为 (15) 当无NEIA汇入透水下垫面时,透水下垫面上降雨强度可表示为 i=iPA (16) 式中:iPA为透水下垫面子汇水区的降雨强度,mm/min。 2.4.1 汇流路径 城市集水区下垫面如何离散将会对雨洪模型的结果产生重要影响,如何将离散的下垫面表示为空间要素,即确定汇流路径,也是影响城市雨洪模拟结果的关键环节。 目前城市雨洪模型坡面汇流机制主要包括以子汇水区为单元进行汇流演算、以DEM栅格为单元进行汇流演算、以结构或非结构化网格为单元进行汇流演算3类方法[32]。考虑各种坡面汇流机制的优缺点,采用以子汇水区为单元进行坡面汇流演算。汇流路径的确定主要包括以下2点[33]:① 子汇水区至出水口汇流路径,即EIA、NEIA、PA子汇水区各自的汇流过程如何计算;② 子汇水区之间汇流路径,即EIA、NEIA、PA子汇水区之间的汇流过程如何计算。不同的汇流路径代表了不同类型子汇水区之间的流动路径的选择[34]。 (1) 子汇水区至出水口汇流路径。EIA子汇水区、NEIA子汇水区、PA子汇水区考虑独立的透水、不透水出口,EIA和PA上产生的地表径流可以独自进入管道节点,但NEIA子汇水区上产生的地表径流不能直接进入管道节点,必须流经PA子汇水区后才可进入管道节点。 (2) 子汇水区间汇流路径。子汇水区间汇流路径,EIA与NEIA之间不能相互流动;PA上的径流可通过EIA流动至管道节点,但EIA上的径流不可通过PA流动至管道节点;NEIA和PA上的径流可相互流动,通过对方流动至管道节点。三者之间汇流路径情况见表1。 表1 子汇水区之间汇流路径情况 因此,模型中坡面汇流路径总共包括5种(图2)。首先,直接汇入管道节点的只能为EIA子汇水区、PA子汇水区2种,NEIA子汇水区不能直接汇入管道节点;其次,各子汇水区之间,NEIA子汇水区可汇流至PA子汇水区,PA子汇水区可汇流至EIA子汇水区,也可汇流至NEIA子汇水区。 图2 坡面汇流路径Fig.2 Overland flow path 2.4.2 坡面汇流模型 径流模拟通过将水量平衡方程与用于估算流量的曼宁方程联立求解来进行[35],在输入降雨过程后,首先对子汇水区内各种类型下垫面进行产流计算和调蓄演算,它们的流量之和,加上其余子汇水区的来水过程,形成该子汇水区汇入检查井的入流过程,经管道、河道汇流计算后得出该子汇水区的出流过程。 坡面汇流模型以子汇水区为单元进行汇流演算,把坡面汇流看作是非线性水库的调蓄过程,即可用下列公式计算出口流量: (17) 非线性水库方程组是非线性方程组,在大部分情况下无法直接求解,但可把两式结合,采用级数解或差分法求解: (18) 式中:ie为入流量,m3/s;O为出流量,m3/s;Sw为滞蓄水量,m3;KS为库容系数;n为非线性水库法中的指数,相关文献中n通常取2/3[12]。 2.5.1 管网汇流 管网内流量演算的基本方程为圣维南方程组,其质量方程和动量方程分别见式(19)和式(20)。 (19) (20) 式中:A为过水断面面积,m2;Q为流量,m3/s;x为沿管道方向的长度,m,H为水头,m;g为重力加速度,m/s2;Sf为摩阻坡度。 将式(19)和式(20)合并,并用差分形式表示为 (21) Ht+Δt=Ht+(∑QΔt)/At (22) 据式(21)和式(22),可依次求解时段Δt内每段管道的流量和每个节点的水头。 如果上游与节点入流超岀下游满管岀流量时,根据管网布设情况,超载水量溢流进入河道或暂时蓄存于调节池,否则漫溢于节点地面,待退水阶段下游管道流量小于满管流量时再流岀[12]。 2.5.2 河网汇流 描述水流在明渠中运动的一维非恒定流基本方程为圣维南方程组: (23) (24) 式中:q为河道旁侧入流,m3/s;BT为当量河宽,m;xr为沿水流方向的河长,m;Z为断面水位,m;K为流量模数,m3/s。 整个河网为若干河道和节点的组合,数值求解河网圣维南方程组,可以求出每个河道指定断面处以及节点上的水位、流量、流速等水力变量。 中国城市化进程快速推进,城市承载了人类社会的主要人口和财富。城市有效不透水面积的增加,导致城市产汇流机制发生改变,本文考虑有效不透水下垫面对产汇流过程的影响,构建了城市雨洪精细模拟模型。 (1) 完善现有确定模型不透水性的方法,将屋顶从整体不透水面积中分离出来,以面要素为单位,先利用影像资料结合ArcGIS确定道路有效不透水面积,再利用城市雨洪精细模拟模型及实测资料率定屋顶有效不透水面积,可快速、准确地确定有效不透水面积。 (2) 综合考虑空间离散程度、模型输出的不确定性及计算耗时三者之间的平衡,合理划分不同下垫面类型,将下垫面划分为有效不透水下垫面、非有效不透水下垫面和透水下垫面3类,并考虑下垫面空间异质性对产汇流过程的影响,确定了模型的结构,选择合理的模型离散方式与程度,从而较为准确地反映不同类型下垫面的产汇流过程,提高模型输出的准确性。 (3) 根据不同下垫面产流特征,对有效不透水下垫面、非有效不透水下垫面和透水下垫面分别采用不同的方法计算产流过程,并设计了不同下垫面产流计算模型。考虑透水下垫面和不透水下垫面汇流过程相互之间的作用,确定子汇水区至出水口、不同子汇水区之间汇流路径,并采用非线性水库法进行坡面汇流计算。针对管网排水及河网汇流特性,建立了管网及河网汇流模型,两者均为求解圣维南方程组的动力波形式。2.4 考虑EIA的坡面汇流计算

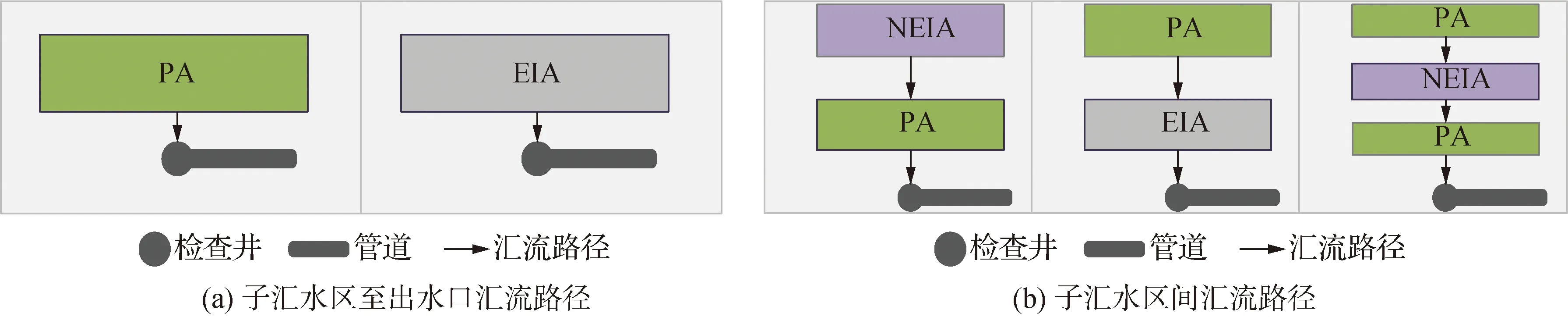
2.5 管网及河网汇流
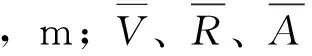
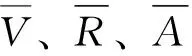

3 结 论

