基于太湖流域模型的城市内涝过程高效模拟

王船海，郑世威，李小宁，陈 凯，翟 月，华 晨，汪 姗，陈 钢

(1. 河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2. 河海大学水文水资源学院，江苏 南京 210098；3. 南京慧水软件科技有限公司，江苏 南京 210036；4. 江苏省水文水资源勘测局常州分局，江苏 常州 213022)

随着城镇化快速推进，目前中国已全面形成了“两横三纵”城镇化战略格局，布局了19个国家级城市群，预计到2025年中国城镇化人口比例达到65%[1]。高度城镇化地区水文特征单元众多，河流水系水文、水动力条件复杂，河流水系连通工程、防洪排涝工程调度等人类活动影响强烈，诸多问题交织导致内涝模拟的难度极大。因此，建立高效、准确、稳定的城市内涝模型对于确定内涝风险、采取调控措施、降低灾害损失具有重要的意义[2-4]。

城市内涝模拟方法主要包括水文学方法、水动力学方法和水文-水动力耦合的方法3大类[5-6]。国内外研究者根据实测降雨—径流数据比较了水文学方法，发现城市雨水地表汇流模型的非线性水库法最优[7-8]，然而其只能计算研究区域的出流流量而未能模拟内涝积水分布的具体过程；水动力学方法主要通过求解二维浅水方程组模拟地表漫流以及通过一维圣维南方程求解管道流量来模拟城市内涝情况[9]，受计算效率限制在较大区域城市的内涝模拟中应用较少；水文-水动力耦合模型采用水文学方法计算子汇水区的产汇流，采用水动力学方法计算管网汇流和地表漫流，该方法主要通过泰森多边形划分子汇水区，难以描述子汇水区的非均匀性，多用于模拟雨水井冒水时的内涝情况而忽视了道路行洪现象，也难以模拟内涝发生的全过程[10]。

在城市内涝水文学模拟方法上，国内外研究者主要基于数字高程模型(DEM)提出计算积水淹没范围的不同方法。Chen等[11]结合降雨—产流模块和基于地理信息系统(GIS)的内涝模块来模拟城市内涝，但GUFIM模型未能模拟管网汇流过程，而是将产流量直接作为内涝模块的输入条件来模拟内涝分布；Thrysøe等[12]开发了基于GIS计算生成积水淹没路径的城市内涝灾害评估模型FloodStroem，相较于MIKE Flood，模型低估了上游内涝而高估了下游内涝情况。城市内涝水文学模拟方法在模拟内涝出现、扩散以及消退过程中存在缺陷，很难模拟内涝的全过程。基于二维浅水方程组的地表漫流水动力模型主要包括LISFLOOD-FP、CityCAT、HiPMS以及FullSWOF_2D等[9，13-15]。这些模型通过求解二维浅水方程组的完整或者简化形式来描述径流在地表上的分布和运动情况，对DEM的精度以及计算成本要求很高。

从20世纪60年代开始，发达国家就开始了水文-水动力耦合的城市内涝模型开发，常见的城市内涝模型主要包括美国环保部开发的城市雨水管理模型SWMM(Storm Water Management Model)及其二次开发模型[16]。例如，国外常用模型PCSWMM、InfoWorks ICM、MIKE Flood[17-18]和国内自主开发的DigitalWater、IFMS Urban及IHUM[19-21]等。黄国如等[21]以SWMM模型与自主研发的二维模型为基础，提出通过水平和垂直方向连接构建的水文-水动力耦合模型，并将模拟结果与InfoWorks ICM进行了比较；Ma等[22]通过SWMM模型参数的实时校正实现了城市内涝的动态模拟；王兆礼等[23]基于SWMM和TELEMAC-2D模型构建一种新的耦合模型TSWM，在复杂城区内涝模拟方面具有良好的适用性和较高的模拟精度；Leandro和Martins[24]应用DLL方法耦合了二维地表漫流模型P-DWAVE和一维管网模型SWMM，实现水文-水动力模型的耦合。模型的时效性和精细度是评估模型适用性的2个标准，然而这2个标准往往相互冲突[25]。SWMM模型在子汇水区概化的过程中往往忽视真实的地形情况以及子汇水区内下垫面的非均匀性而增大模型的不确定性；模型中未能实现管网、河道与地面的耦合因而不具备模拟城市内涝全过程的能力，目前主要用于城市管网排水能力评估和模拟由于管道排水能力不足引起的雨水井冒水而导致城市内涝的情况。

本文基于太湖流域模型中的高效模拟算法和二维水动力算法建立试验基地城市内涝模型，并根据监测数据对模型进行率定和验证；通过深入分析试验基地降雨事件下内涝模拟的精度与可靠性，对城市内涝高效模拟方法的适用性进行评估。

1 模型原理

太湖流域模型是以太湖流域为原型案例构建的一个从山丘区到平原区的多要素、多尺度、多过程的完整水循环精细化模型[26-30]，历经40多年的开发研制，已形成完整的模型理论与架构体系，是完全自主研发的，能解决不同复杂下垫面水循环、水质、泥沙问题的一体化模型软件。太湖流域模型提出了分布式架构体系与水文特征单元的新概念，将流域内产汇流机理相同的区域分别概化为山丘区子流域及坡面单元、山丘区河道单元、平原区坡面单元、平原区河道单元、闸坝工程单元等[31]，针对每类水文特征单元采用最合适的模型算法进行模拟，对各种类型水文特征单元进行耦合，使其能够成为一个完整的模型体系。

1.1 城市水文特征单元概化

由于受到道路与建筑的阻隔，城市内涝主要呈现斑块化、局域化的特点，太湖流域模型中以雨篦子为核心构建排水管网水动力模型体系。如图1所示，研究区域结合DEM与雨篦子分布情况进行汇水区划分，每个汇水区作为一个基本单元，包括区域产流单元、调蓄单元、雨篦子、管道等要素。在产流阶段按照水体、绿地、建筑以及道路和广场4种下垫面类型进行产流模拟，采用单位线方法模拟城市水文特征单元内的汇流过程，径流经过坡面汇流过程后通过雨篦子进入管道，进而流向下游管道或河道。

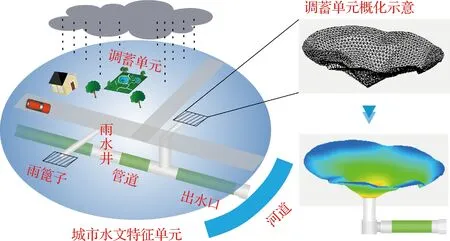
图1 基于雨篦子的城市水文特征单元概化Fig.1 Conceptualization of urban hydrologic unit based on grate inlet

1.2 城市内涝模拟

与SWMM模型不同，太湖流域模型中根据地形将调蓄单元概化为蓄水面积随水位变化的节点，因此，可以根据调蓄单元内的水位计算积水淹没深度和空间分布。降雨后地表产生径流汇集到调蓄单元出口并通过雨篦子进入管道，当管道排水能力不足或者雨水井冒水时调蓄单元内积水增加，进而模拟实际的内涝情景。城市水文特征单元中调蓄单元、雨篦子以及管道的耦合概化方法如图2(a)所示，根据水量平衡公式计算调蓄单元内的水量变化：

(1)

式中：q0为降雨产流，m3/s；Q为雨篦子过流量，m3/s；AS(Z)为随水位变化的调蓄单元面积，m2；ZV、ZV0为调蓄单元的计算水位与初始水位，m。

太湖流域模型中雨篦子的过流能力计算分为3种不同的情况[32]：当地面水深较浅未完全淹没雨篦子时采用堰流公式(式(2))计算，如图2(c)所示；当地面水深增加将雨篦子完全淹没后采用孔口流量公式(式(3)、式(4))计算，如图2(d)和图2(e)所示。

(2)

(3)

(4)

式中：C为雨篦子过流常数；L为雨篦子过流长度，m；g为当地重力加速度，m/s2;Am为雨篦子过流面积，m2；H为雨水井深度，m；h为地表积水深度，m；HP为雨水井水深，m。

通过对雨篦子过流量公式做线性化处理[33]，可得雨篦子过流量与调蓄单元计算水位以及排水管道水位(ZP)的关系如式(5)所示，其中α、β为相关系数，θ为余项。

Q=αZV+βZP+θ

(5)

将式(1)改写差分形式，并与式(5)联立消去ZV可得雨篦子过流量与管道水位之间的关系：

Q=αWZP+βW

(6)

其中：

(7)

式中：Δt为时段长度，即计算时间步长，s。

由式(6)可知，若管道水位已知，即可求出雨篦子过流量。太湖流域模型中管网计算过程为：通过边界条件得出管道各断面的追赶关系，进而表达为与管网节点水位的关系，节点的水力要素通过联解得出后，回代求出各管道断面的水位和流量。太湖流域模型中针对城市排水管网系统的明满流共存这一计算难点，从一维圣维南方程组的物理意义出发，推导了适用于有压管流的方程组表达形式，提出了当量宽度的概念和计算方法，修正了Preissmann窄缝法中的窄缝宽度公式，进而统一了明渠和有压2种情况下的方程组，实现了对明满过渡流的有效数值模拟[34]。

太湖流域模型中的城市水文特征单元也可以通过求解二维浅水方程组来模拟地表内涝积水情况[35]。如图2(b)(q0i为二维网格单元中每个网格单元的流量，m3/s)所示，将每个网格视作节点，通过地表产流模块计算出网格节点内的产流流量，然后通过求解二维浅水方程模拟地表径流汇流到雨篦子并进入雨水管的过程。与高效模拟方法类似，雨篦子过流量与相邻二维网格水位(Zcell)以及管道水位的关系如式(8)所示。

图2 调蓄单元、二维网格单元、雨篦子以及管道耦合概化Fig.2 Conceptualization of storage unit，two-dimensional cell unit，grate inlet and pipe coupling

Q=αZcell+βZP+θ

(8)

采用与式(6)类似的处理方式，得到Q与ZP之间的关系；随后采用直角坐标系下矩形网格的控制体积法对浅水方程组进行数值离散，得到二维相邻网格节点之间的交换流量与网格节点内水位的线性关系；分别对连续性方程和动量方程组进行离散来构建待求解的线性矩阵；联立构建的求解矩阵和上下游边界条件即可得到1组完备的线性方程组，随后通过矩阵追赶法求解联立的矩阵，最终求得每个网格内的水位值[36]。

2 研究区域与数据

双桥浜城市产汇流与内涝试验基地位于江苏省常州市(31°48′04″ N，119 °57′06″ E)中北部，属太湖流域武澄锡虞区较为典型的城市小区。研究区内地势平坦，略呈西北高、东南低之势，地面高程为-1.13～12.35 m(1985国家高程基准)，研究区域总面积约为1.62 km2，如图3(a)所示。双桥浜河道由北南方向贯穿试验基地，并在润德半岛附近分成2支，河道总长1.91 km(其中西支0.27 km)，河道宽约20.0 m，水面面积约3.82 hm2，下游出口汇入北塘河处建有泵站，设计流量为4.0 m3/s。

图3 试验基地基础信息Fig.3 Basic information of experimental site

双桥浜试验基地的基础数据包括下垫面数据、管网数据和地面高程数据等。研究区域地面高程概况如图3(b)所示，分辨率为0.5 m。从地面高程和管网分布可以看出研究区域相对封闭且不受客水的影响，便于进行内涝模拟分析。现有2个HOBO雨量计用于监测区域内的降雨数据，其位置如图3(a)中①与②所示；由于研究区域内管网与河道之间的耦合模拟十分重要，因此，分别在红莲桥管网入河口处(图3(a)中入河口③)与盛世名门管网入河口处(图3(a)中入河口④)设置了管道水位流量监测设备，用于监测2处管道入河口的水位、流量数据；此外，还设有1套ADCP河道自动测流装置，监测双桥浜出口处水位数据，其位置如图3(a)中⑤所示。

3 模型建立与率定验证

3.1 城市内涝模型建立

如图4(a)所示，根据土地利用信息网格化研究区域，网格分辨率为6 m，网格数总共为44 323个。如图4(b)所示，该研究区共概化308个雨篦子、294段管道以及3条河道，图4(b)圈中为与河道连接的管道断面。根据每个网格的地表高程值使用城市水文特征单元自动划分功能为每个雨篦子分配对应的汇水区，如图4(c)所示，其中不同颜色的色块表示不同雨篦子对应的汇水区，无色块处表示该地区产流通过沿河短管(长度<50 m)就近直接流入河道。

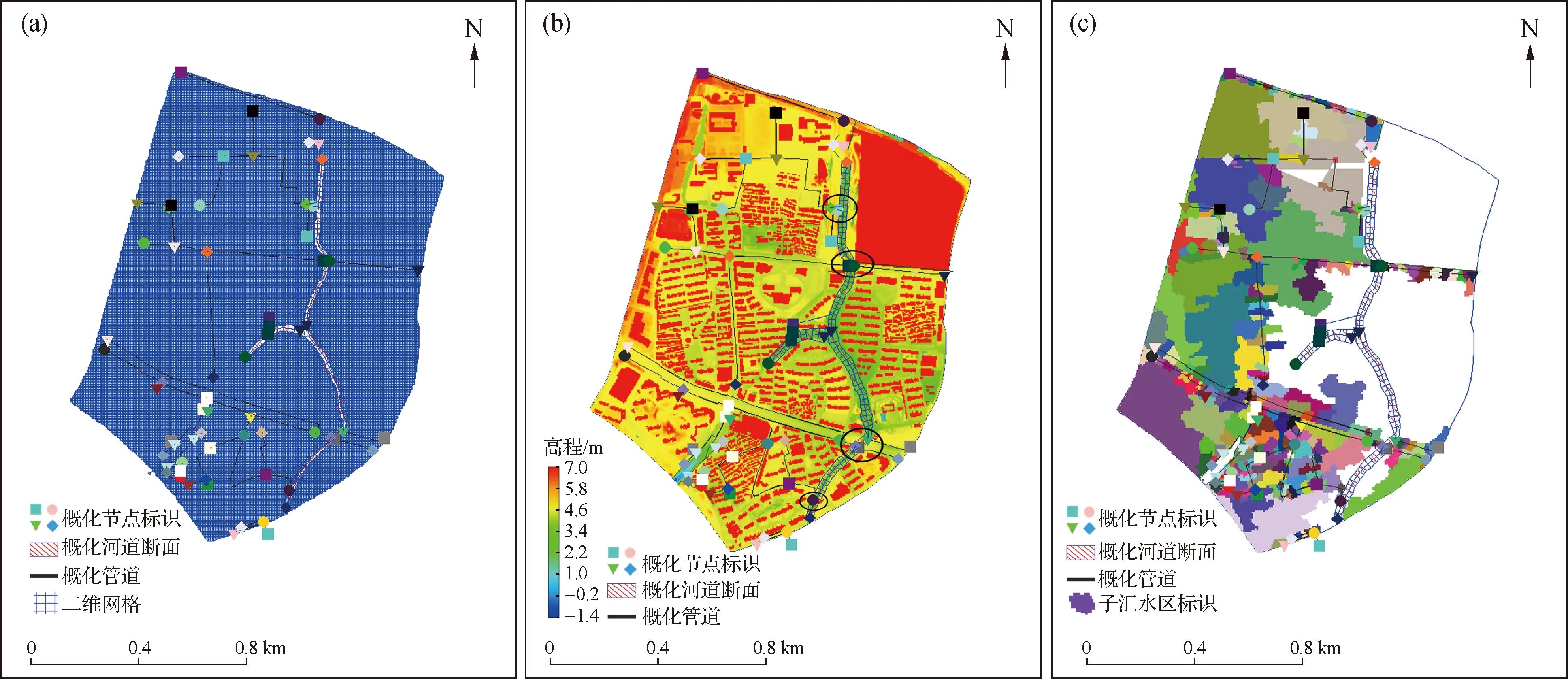
图4 城市内涝模拟模型信息Fig.4 Basic information of urban flood inundation model

在高效内涝模型基础上添加该研究区域的二维模型要素，同样设置研究区域二维网格分辨率为6 m，在每个雨篦子处将其对应的管道断面与网格建立雨水排水口联系，得到该研究区域的二维水动力内涝模型。二维水动力内涝模型除地表漫流计算方法与高效内涝模拟模型不同外，其余模型设置均与高效内涝模拟模型采用同1套参数设置。

3.2 模型率定和验证

选取红莲桥处入河口管道水位、盛世名门内管道入河口管道水位和流量进行率定与验证。其中，选取3个降雨事件(20200711、20200720和20200915)进行模型率定，选取2个降雨事件(20200705和20200706)进行模型的验证。通过纳什系数(ENS)、相对总径流量误差(ERR，%)、相对流量峰值误差(ERP，%)以及峰值时间误差(EPT，min)4个指标评价模型率定与验证结果。表1统计了用于率定和验证的降雨事件特征，降雨量范围为5.2～74.2 mm，降雨历时最短为145 min、最长为320 min。其中，用于率定的降雨事件中包括1场前峰型降雨和2场后峰型降雨，用于验证的降雨事件中有1场前峰型降雨和1场后峰型降雨。总体而言，选取用于率定和验证的降雨事件雨量大小、历时长短和雨型分布较为合理，能够满足模型率定和验证的需求。

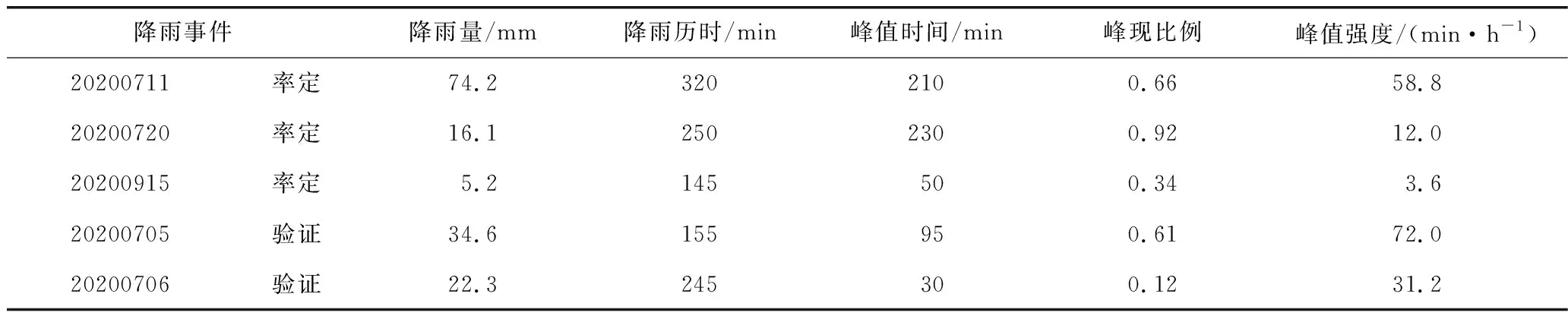
表1 率定和验证降雨事件特征统计

4 结果分析与方法比较

4.1 率定和验证结果

监测区域内2处入河口平时均处在淹没状态，入河口内的水位会随着河道水位变化而同步变化。河道下游泵站会周期性开启进行阶段性抽水，导致该河道水位呈现周期性的起伏变化，同时引起管道入河口处的流量波动和水位的同步变化。因此，在没有降雨时，管道入河口处的水位和流量受到河道水位变化影响呈现一定的起伏波动；当降雨时，管道入河口处的水位和流量变化受河道水位变化与降雨同时影响。20200706场次与20200711场次降雨盛世名门管道入河口断面处的模拟结果如图5所示。

图5 20200706和20200711场次降雨模拟结果Fig.5 Simulation results of rainfall events for 20200706 and 20200711

可以看出，在20200706降雨事件中，盛世名门入河口处水位随着降雨过程先缓慢升高后逐渐降低，这是由于双桥浜泵站开启导致河道水位下降，盛世名门管道入河口处的水位也随之降低。图5(a)也可以看出模型模拟的管道流量会出现负值，即往复流现象，这是由于入河口处的流量受到区域内降雨和河道水位顶托的共同作用。在20200711降雨事件中，盛世名门处入河口水位随着降雨而逐渐升高，由于此时双桥浜泵站未开启，盛世名门入河口流量主要受到降雨的影响。表2列出了5场降雨事件的水位率定和验证结果，5场降雨盛世名门管道断面处的流量率定和验证结果如表3所示。

表2 水位率定和验证结果

表3 盛世名门管道断面处流量率定和验证结果

从各场次降雨模拟结果图可以看出，本次水位与流量模拟结果均较符合实测情况，其中水位模拟结果ENS值均在0.85以上，但是通过流量模拟结果可知，部分流量模拟的结果ENS值在0.5以上。分析原因可能为：

(1) 实测流量间隔为10 min，模拟结果输出间隔为5 s，因此，实测流量过程线相对比较平滑，然而中间时刻的流量波动却未能测得。

(2) 由于管道长期处于淹没状态，受河道水位波动影响而产生往复流，但监测设备并不能测量往复流量。

(3) 受河道顶托影响管道入河口的流量较小，容易导致相对流量峰值误差的绝对值偏大，以20200705场次降雨为例，计算流量峰值为0.108 m3/s，实测流量峰值为0.103 m3/s，两者流量峰值仅相差0.005 m3/s，但是相对误差却达到了4.85 %。

4.2 城市内涝模拟结果分析比较

论文选取了监测事件中降雨量较大的2场降雨进行基于太湖流域模型的城市内涝模拟方法分析，内涝分析事件包括20200705和20200711场次降雨。20200705场次降雨量大致相当于常州市暴雨强度计算公式计算的一年一遇降雨量(39.9 mm)；20200711场次降雨量大致相当于常州市暴雨强度计算公式计算的50年一遇降雨量(72.3 mm)。图6显示了20200705和20200711场次中高效算法与二维算法模拟的每个网格内淹没水深(d)的比较。图6中统计了每个网格内的淹没水深并做散点图，其中不同颜色表示数据点的密集程度。图6(a)中，20200705场次事件的模拟中高效算法与二维算法的模拟最大淹没水深相关性系数(R2)为0.14，均方根误差(ERMS)为0.06 m。图6(b)中，20200711场次事件中高效算法与二维算法的模拟最大淹没水深R2为0.19，ERMS为0.09 m。由于2种方法计算原理不同，二维算法会模拟降雨产流后的汇流过程，而往往在汇流过程中的水深是比较小的，因此，在剔除水深小于0.15 m的数据点后，20200705场次的模拟结果中高效算法与二维算法的R2为0.53，ERMS为0.23 m；20200711场次的模拟结果中高效算法与二维算法的R2为0.43，ERMS为0.18 m。这也说明由于计算原理的不同，高效算法和二维算法在小水深模拟时有一定的差别，但2种方法模拟的淹没水深在大于0.15 m的区域一致性较高。

图6 20200705和20200711场次高效算法与二维算法最大淹没水深对比Fig.6 Comparison of simulated water depth in 20200705 and 20200711 events

图7显示的是场次20200711中高效算法与二维算法的最大淹没水深分布情况。通过对比2种算法模拟水深的分布情况可以看出：研究范围内的区域Ⅰ、区域Ⅱ、区域Ⅲ和区域Ⅳ对应的模拟结果较为相近，其中，区域Ⅱ和区域Ⅳ为2座下凹式立交桥的桥区，淹没面积比较大，淹没深度模拟结果也相近；区域Ⅰ为城中村和小学，城中村地势低洼加之内部缺少排水设施，学校内产生径流很难排入附近管网而排到城中村区域，因而造成区域Ⅰ内的淹没水深较大，这也与事后内涝调研结果相符；区域Ⅲ为住宅区域，内部下垫面硬化程度较高，径流系数过大加上排水管网能力较低，导致此区域内的淹没水深较大。结合图6和图7可以发现，在相同位置高效算法模拟的水深一般会大于二维算法的模拟淹没水深。这是由于二维算法中模拟了地表漫流过程，地表水深的分布较为分散，而高效算法中只模拟地表积水的分布，因此，高效算法模拟的地表淹没水深较为集中且一般会大于二维算法模拟的地表淹没水深。

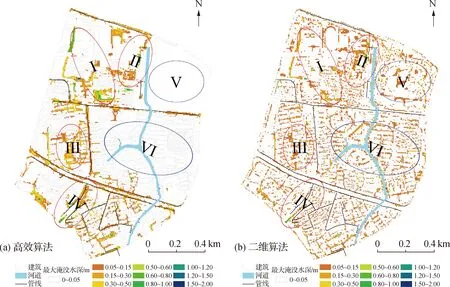
图7 20200711场次最大淹没水深分布模拟结果Fig.7 Distribution of simulated water depth in 20200711 events

图7中区域Ⅴ和区域Ⅳ高效算法和二维算法结果的不同主要是由于区域靠近河道，区域内产生的径流通过很多沿河道的小支管(长度<50 m)直接排入河道中。在这种情况下，高效算法中区域Ⅴ和区域Ⅵ产生的径流直接进入河道，因而很少积水；二维算法则会模拟降雨产流后通过地表漫流进入支管和河道的过程。因此，高效算法中区域Ⅴ和区域Ⅵ内基本上d<0.05 m，二维算法中的大部分0.05≤d≤0.15 m。

表4分类总结了20200705和20200711场次降雨事件中淹没水深的模拟结果，并针对高效算法和二维算法的模拟水深进行了对比。表4中可以看出高效算法和二维算法的不同淹没水深统计面积非常接近，20200705场次中2种方法不同水深面积R2为0.99，ERMS为2.95 m；20200711场次中2种方法不同水深面积的R2为0.99，ERMS为4.99 m。总体而言，高效算法和二维算法模拟的城市内涝中不同淹没水深范围的结果是非常接近的。表4中统计了不同淹没水深范围的斑块数用以计算不同淹没水深范围的破碎度即分散情况。可以看出，二维算法的模拟结果破碎度总是大于高效算法的模拟结果，这也体现了城市内涝往往呈现分散化、斑块化以及局域性的特征。

表4 不同淹没水深高效模拟与二维模拟算法结果总结

5场降雨事件模拟均通过笔记本电脑计算完成，建模型中高效算法和二维算法共用同一套网格，网格大小为6 m × 6 m，研究区域内总共网格数目为44 323个，电脑CPU为Core i5-6300HQ，内存为8 GB 2 133 MHz。表5统计对比5场降雨事件中的高效算法和二维算法所用的时间，可以发现在模拟相同历时的降雨事件时二维算法所需要的时间是高效算法的780～1 275倍，高效算法具有更高的时效性，而二维算法的计算效率较低。二维算法中计算耗时往往是模拟历时的2.17～2.83倍，即计算耗时/模拟历时大于1，因此在计算机硬件水平一般的情况下很难及时输出城市内涝模拟的结果；高效算法中计算耗时/模拟历时远远小于1，说明高效算法能够实现真正的城市内涝快速模拟。

表5 各个事件模拟时效性统计

5 结 论

基于自主研发的太湖流域模型中城市水文特征单元概念，以常州市双桥浜城市产汇流与内涝试验基地为对象，分别构建了城市内涝高效模型和城市内涝二维水动力模型。选用5场实测降雨事件对模型进行率定和验证，对两者的模拟结果与实测资料进行了对比分析，主要结论如下：

(1) 2种方法管道水位与流量模拟结果与实际情况较为吻合，均具有良好的精度和可靠性，可应用于城市地区内涝模拟。

(2) 比较两者内涝模拟结果发现由于受到城市道路、建筑等阻隔作用，城市内涝区域呈现斑块化和破碎化的特点而非平原区洪涝的连续一致。此外，城市内涝主要发生在局部低洼处，内涝积水的流动性不强，这也从侧面验证了城市内涝高效模型中城市水文特征单元的概化符合实际情况。

(3) 通过对城市内涝高效模型与二维水动力模型的时效性进行对比分析，在两者的模拟结果较为接近的情况下，城市内涝高效模型的时效性远远高于城市内涝二维水动力模型，可适用于大范围区域城市内涝模拟。