高速远程滑坡沿程速度演化与冲击力分布研究
——以三溪村滑坡为例
陈 果,钮志林,樊晓一,3,胡晓波
(1.西南科技大学土木工程与建筑学院,四川绵阳 621010;2.中国公路工程咨询集团有限公司,北京 100089;3.西南石油大学土木工程与测绘学院,四川成都 610500;4.中国科学院、水利部成都山地灾害与环境研究所,四川成都 610041)
引言
高速远程滑坡具有巨大的体积,运动速度快,启动突然的特点[1-2],在运动过程中常表现出异常的高速运动和流动性强的特征,是自然界中具有极端破坏力的地质灾害现象之一,常造成严重的人员伤亡和财产损失,严重威胁山区建筑安全和人民财产安全[3-4]。国内外针对高速远程滑坡的研究主要采用野外调查和遥感勘测、理论计算、实验室模型实验以及数值模拟等技术手段,分析其启动机制、动力学过程以及堆积特征等。理论计算如谢德格尔法,能计算滑坡的运动距离和速度。野外调查和遥感监测可以直接获取滑坡的形态特征和部分运动参数,例如Perinotto等[5]基于对La Reunion岛的滑坡堆积体的实地考察,提出大块石崩解释放的大量弹性势能以及细粒碎屑的润滑作用能显著增加滑体的动能;李华等[6]采用野外调查等手段,分析滑坡基本特征和滑坡体结构,研究公路切坡和持续强降雨因素对滑坡稳定性的影响。实验室模型实验能在缩尺比例上研究滑坡的变形和破坏机理,如冷晓玉等[7]利用滑坡模型试验研究不同坡角和颗粒级配对滑坡运动的影响机制。赵运会[8]等通过开展室内滑坡模型试验,分析岩土体类型、斜坡坡度和滑体体积对滑坡运动距离、速度及堆积体厚度的影响。
由于滑坡发生时间和位置的不确定,其致灾速度和冲击力的实时监测存在难度,缺乏对致灾强度的准确评估。运用数值模拟,以滑坡最终堆积特征为参照,模拟其运动的过程,反演致灾过程中的运动速度和冲击力,为滑坡致灾强度的研究提供了有力的工具。Li等[9]基于MPM法,考虑速度弱化摩擦效应和应变软化效应模拟大光包滑坡,但相比于物质点法,离散元法基于细观力学出发,考虑了颗粒的不连续性,能够较好的模拟大变形、大位移,对于模拟高速远程滑坡运动具有较好的适用性。Tang等[10]利用PFC2D,研究摩擦系数和颗粒粘结强度对集集滑坡数值模拟的影响,并进一步分析润滑机制。Wang等[11]运用PFC3D并考虑地震的因素,研究红石岩滑坡速度、堆积特征。毕钰璋[12]等采用离散元软件对四川绵竹清平文家沟地震滑坡的运动过程进行了研究,并设置不同摩擦系数条件作为变量,研究滑坡堆积情况以及防护结构体对滑坡的耗能作用。肖思友等[13]在离散元软件中采用Hertz-Mindlin模型建模,模拟防护结构为柔性网和刚性挡墙在受到滑坡冲击时,冲击力及动力响应过程;Bi[14]等使用离散元法,设置挡板列、排的数量和间距作为变量,研究滑坡对挡板产生的冲击力以及挡板对滑坡的耗能作用。张睿骁等[15]运用三维离散元软件,研究3种不同拦挡结构对滑坡运动和堆积特性的影响,得到较好的结果。
室内模型试验能较好的研究冲击力随岩土体参数和坡度的变化规律,但针对滑坡巨大的体积,室内模型试验一般采用较小的相似比,导致滑坡地形地质条件的简化,对呈现滑坡的实际运动特征存在一定的局限性。数值模拟可以通过匹配滑坡参数实现堆积结果与实际滑坡的一致性,来反演滑坡致灾参数,在分析滑坡致灾机制方面得到了广泛运用。本文以典型滑坡灾害——三溪村滑坡为例,研究三溪村滑坡沿程速度演化和冲击力分布。
1 三溪村滑坡概况
1.1 滑坡概况
三溪村滑坡位于四川省都江堰市中兴镇三溪村,处于龙门山断裂带与成都平原过渡地段,滑坡体呈NE方向展布。2008年5·12汶川地震导致三溪村大字岩平台上部岩土体开裂形成贯通性裂缝,在强降雨的影响下,大量水体渗入到裂缝中,在动水压力和静水压力的作用下,山体结构破坏失稳,形成灾难性高位滑坡。滑坡前后缘垂直高差377 m,后缘到前缘的水平距离为1 240 m,滑源区1.47×106m3的山体发生整体滑动,在沿程运动过程中破碎解体,导致运动堆积区内11户居民建筑被毁、52人死亡、109人失踪[16],造成巨大的人员伤亡及财产损失。三溪村滑坡属于典型的沟道偏转型滑坡,其滑坡方向由57°转向350°(图1)。
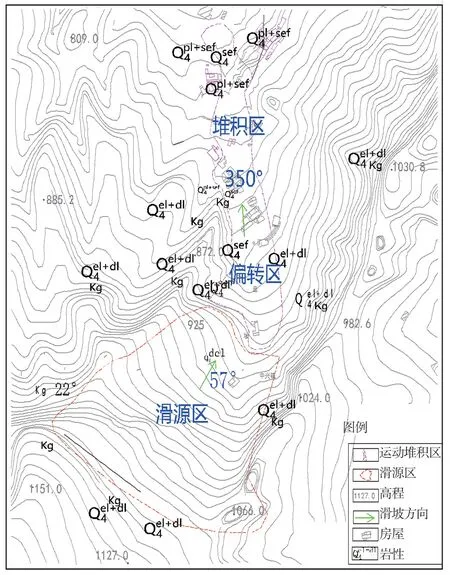
图1 三溪村滑坡平面图Fig.1 Landslide plan of Sanxi Village
1.2 三溪村滑坡岩性
三溪村滑坡区主要出露白垩系灌口组(Kg)和第四系地层(Q)。其中白垩系灌口组(Kg)分布于三溪村滑坡整个区域,在滑坡区上部主要以黄棕、红棕色砂岩、泥质粉砂岩为主,滑坡区中下部主要以砾岩为主。三溪村滑坡沟槽内主要分布堆积层(Q4sef),其主要物质为含碎石(巨石、漂石)的粉质粘土,粉质粘土主要以褐黄色为主,软塑~流塑状态、饱和,碎块石(巨石、漂石)主要为强风化砂岩、粉砂岩,无分选性,磨圆度差,直径一般5~20 cm,漂石、巨石多大于80 cm,个别达数米大。其中巨石、漂石的含量约为20%~25%;沟槽的底部及沟口前缘两岸的岸坡上主要分布第四系泥石流积、洪积层(Q4pl+sef),其主要物质为含砾石粉质粘土;滑坡坡面上主要分布第四系滑坡堆积层(Q4del),其主要物质为粉质粘土夹碎块石土;斜坡表层主要分布第四系残坡积层(Q4el+dl),其主要物质为粉质粘土夹碎块石土。
2 模型建立和参数标定
2.1 离散元介绍
PFC作为离散元方法的一种,由Cundall(1979)定义[17]。在PFC程序中离散颗粒能独立产生运动和旋转,在计算过程中每个颗粒都能独立自动识别接触并产生运动。PFC在岩土体领域应用广泛,主要用于模拟离散颗粒的运动和相互作用。
2.2 建模过程
PFC3D滑坡模拟中常采用ball-ball法和ball-wall法建模,ball-ball法指用ball构建滑体和滑床及边界,ball-wall法指用ball构建滑体,而滑床及边界由wall构建。本研究采用ball-wall法模拟三溪村滑坡,该法所需颗粒较少,提高模拟的效率,适用于模拟滑床及边界已知的滑坡。如图2所示滑坡体物源区被分成了9块区域(G1-G9),用不同颜色表示,用以追踪研究堆积区物质的来源。因本文主要目的是研究三溪村滑坡前缘速度和滑坡对山区房屋的冲击致灾机制,所以主要监测前缘颗粒。选择较少的监测点会存在较大的误差。因此每个部分选择4个监测点(P1-12),共计12个监测颗粒。
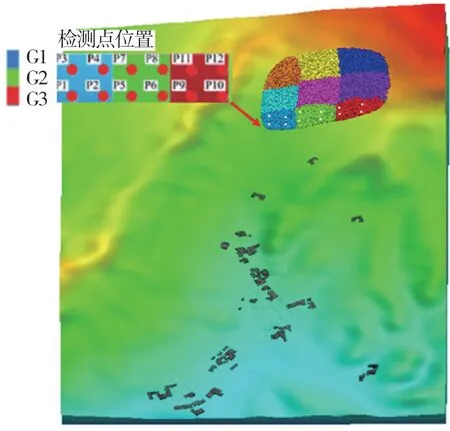
图2 三溪村滑坡模型图Fig.2 The model of Sanxi Village landslide
2.3 接触模型
PFC中内含多种接触模型,本研究选择平行键粘结模型(Linearpbond),该模型其粘结组件和线性元件平行,可以在不同颗粒之间传递接触-接触间的弹性相互作用(类似于环氧树脂胶合玻璃珠、水泥间骨料的黏结)。因此平行键粘结模型在滑坡、泥石流、崩塌等地质灾害中应用广泛[18-19]。
2.4 参数标定
PFC中参数采用的是颗粒之间的微观参数,而实际岩土体中的宏观参数很难与微观参数对应,颗粒不能直接实现宏观材料的性质,但二者之间存在一定的联系。常见的参数标定方法有试错法和通过三轴实验获取应力应变曲线,并和宏观参数做比较,但试错法尝试次数多且标定参数可能造成比较大的误差。利用PFC建立三轴实验进行微观参数标定,成为广大学者研究灾难性滑坡的有效工具。
PFC中颗粒是刚性物质,不能实现模拟颗粒破碎及磨损,颗粒之间碰撞产生的非弹性能量耗散难以直接模拟,所以引入阻尼来加速数值解的收敛和实现能量的耗散。在平行键粘结模型中,有效粘结模量与和杨氏模量有关,颗粒刚度比和泊松比有关,平行粘结强度和单轴压缩应力有关,利用PFC3D中的伺服机制设置无侧限单轴压缩实验,获取应力应变曲线图3,通过和室内试件的参数对比,校核数值模拟的微观参数,查阅文献得到白垩系粉砂岩[20-21]的单轴抗压强度约61 MPa,杨氏模量约11.06 GPa,密度约2 300 kg·m-3,无侧限单轴压缩实验得到的结果同室内试验参数一致,获得数值模拟参数见表1。
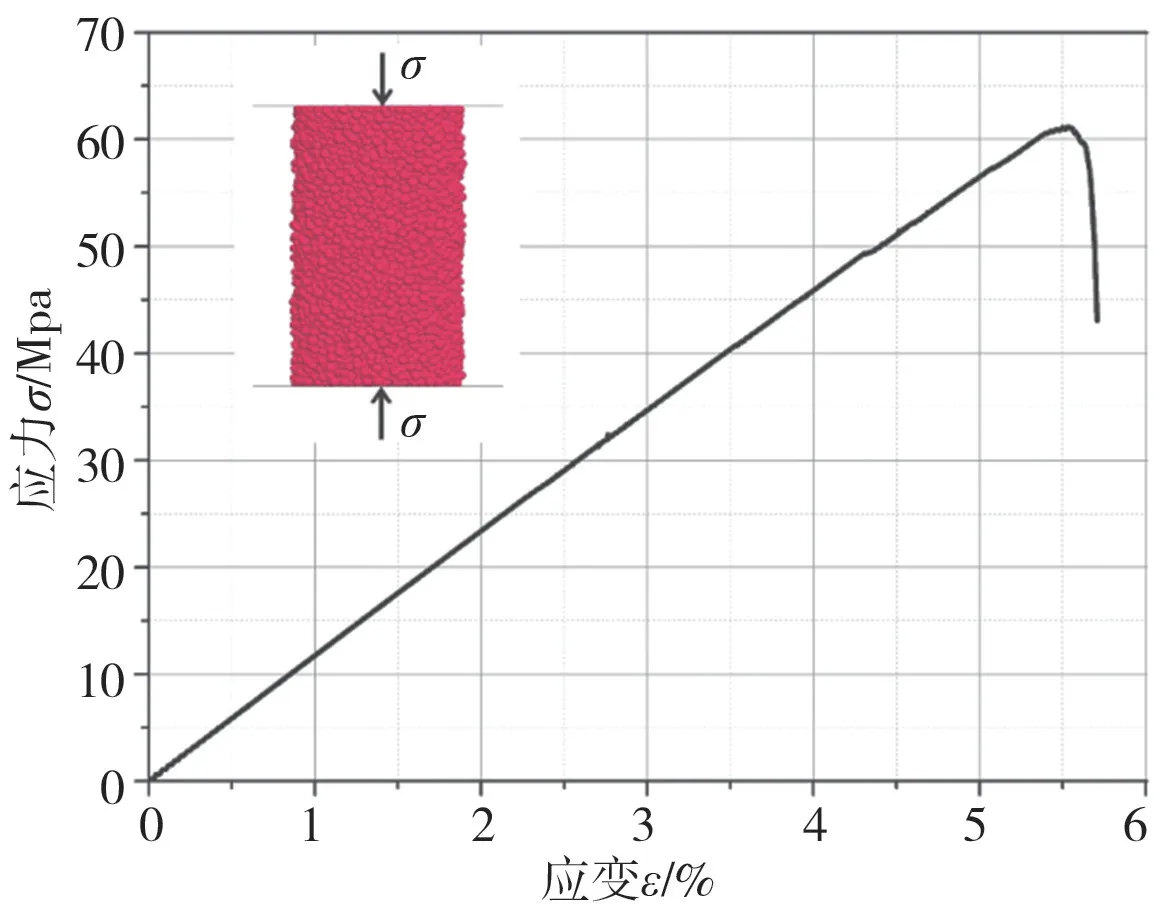
图3 单轴压缩试验Fig.3 Uniaxial compression test
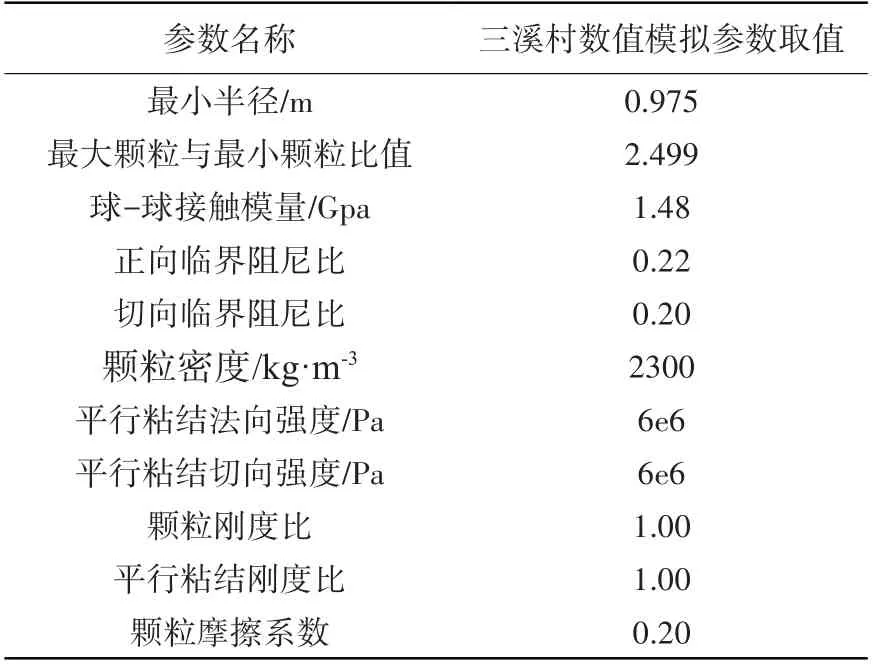
表1 数值模型微观参数Table 1 The numerical micro-parameters of the PFC model
2.5 模拟结果
根据三溪村滑坡地形(图1),滑坡发生后的影像(图4)和文献资料(图6)[16],比较数值模拟的最终堆积结果(图5、图7),表明数值模拟的堆积形态符合实际滑坡堆积特征,滑坡堆积区后缘高程850 m,前缘高程740 m,堆积长度约560 m,宽50~140 m,堆积厚度5~15 m。
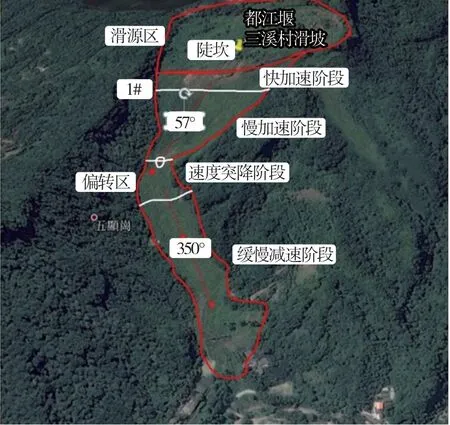
图4 滑坡发生后的遥感影像图(Google Earth)Fig.4 Remote sensing image after landslide
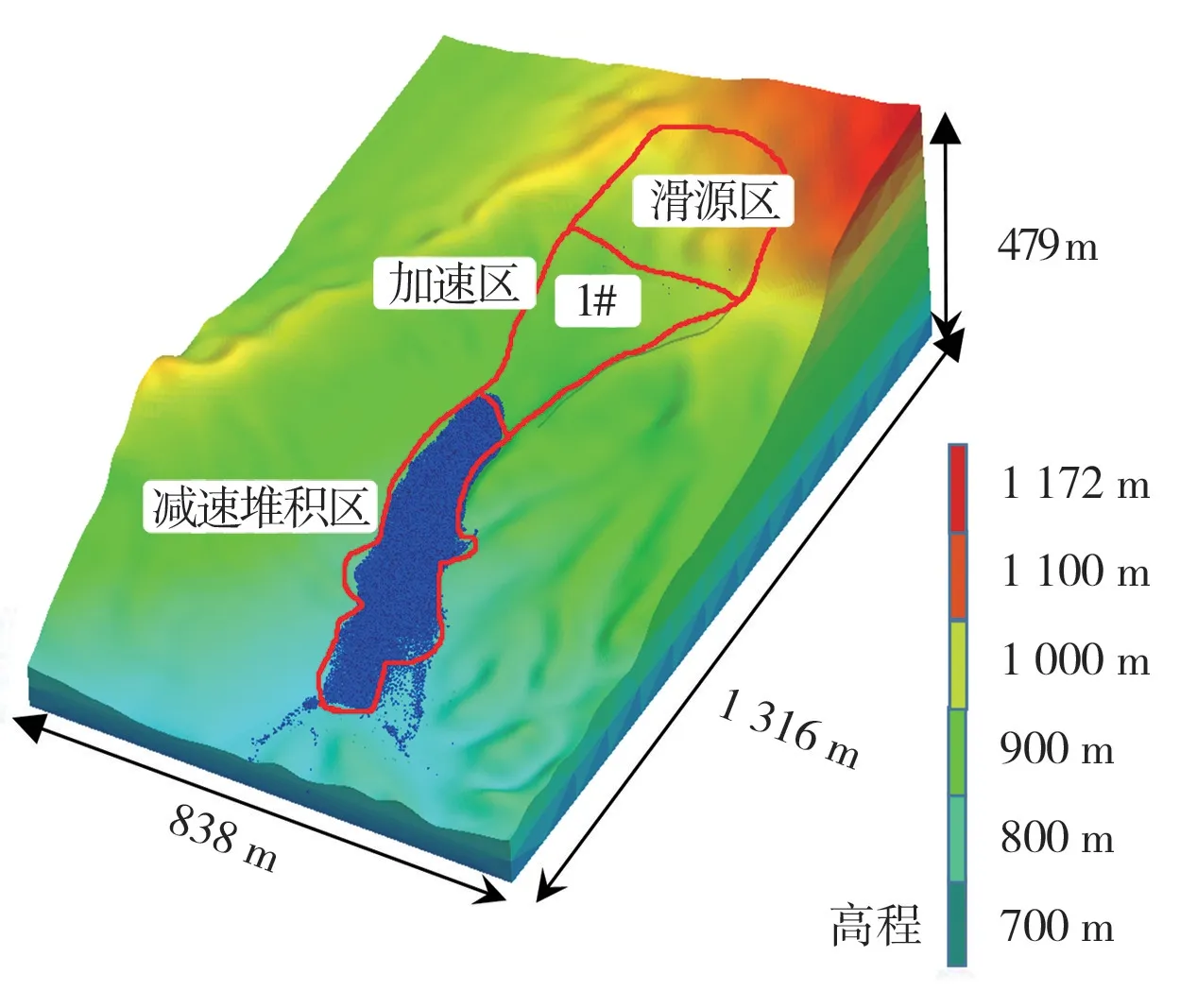
图5 数模拟堆积图Fig.5 Numerical simulation stacking diagram
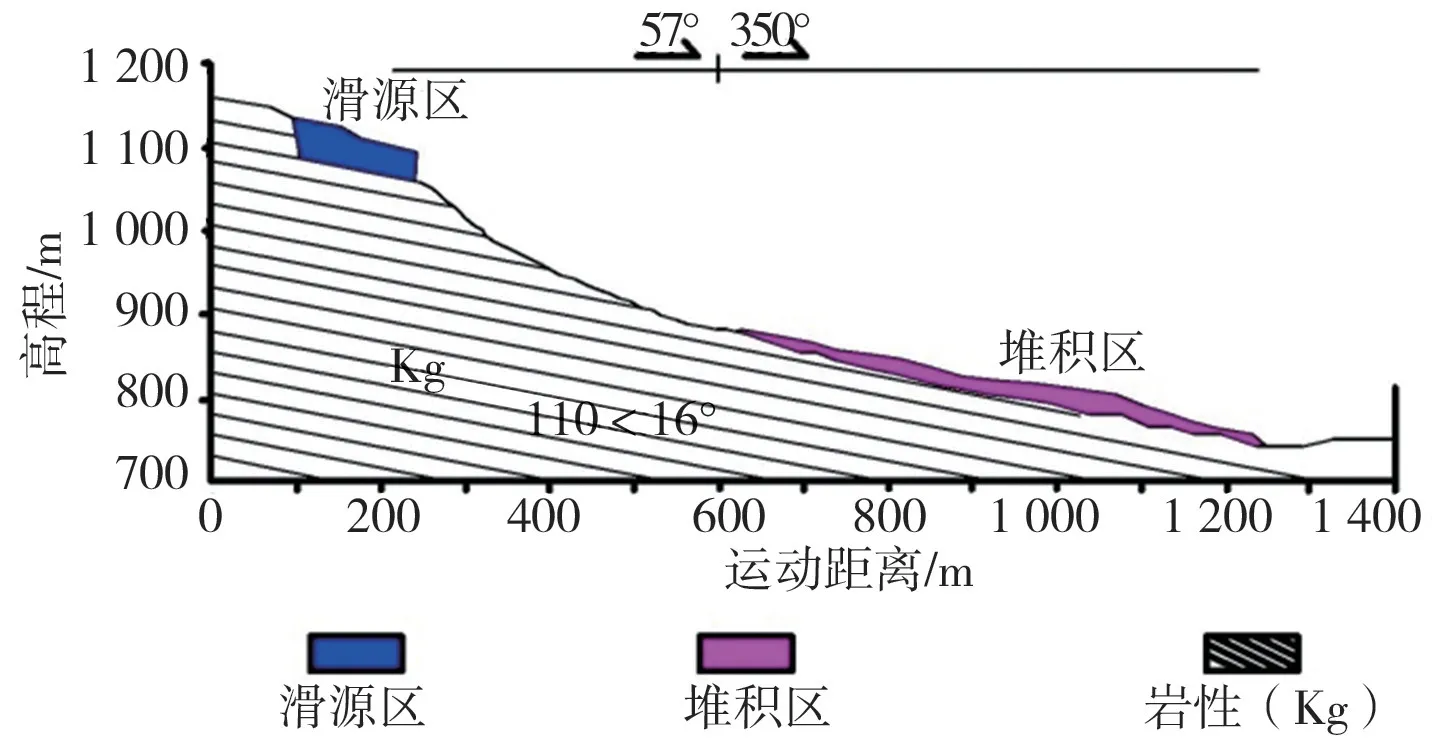
图6 滑坡剖面图Fig.6 Landslide profile
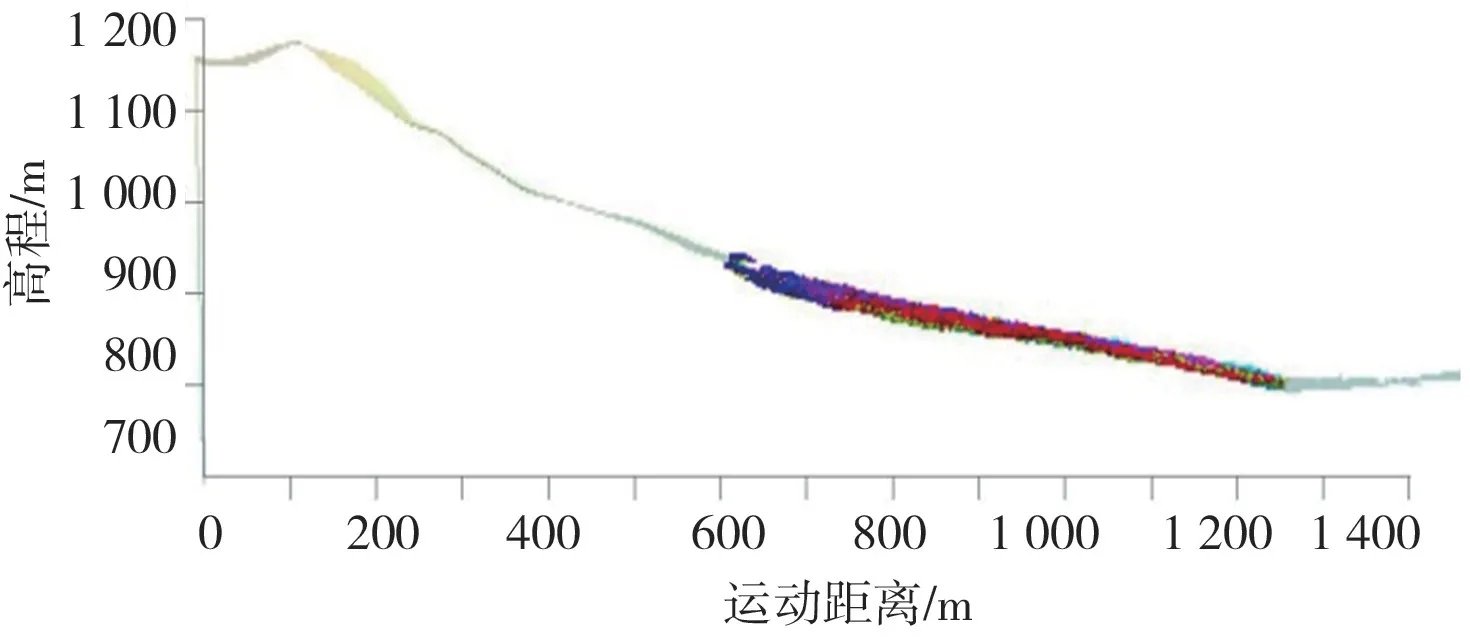
图7 数值模拟剖面图Fig.7 The profile of numerical simulation
3 三溪村滑坡前缘运动速度特征
三溪村滑坡启动、加速运动后,土体快速崩落、破碎。在撞击右侧山体后,滑坡的运动由北东方向转向北西方向,沿程冲击损毁和掩埋山区农房建筑,到最终停止堆积,模拟结果表明,三溪村滑坡的运动时间约为80 s(图8),滑坡启动后,在重力的作用下,岩土体崩塌破碎,经过陡坎地形后速度快速增加,运动到7.5 s时速度达到20 m/s。后受狭窄沟道的影响,岩土体速度增速降低,经过19.5 s后,滑坡体进入沟道偏转区,速度增至峰值速度35 m/s。受到沟道偏转区地形的影响,岩土体和山体激烈碰撞,滑坡主滑方向改变为350°,T=36 s时,滑坡大部分岩土体到达沟道偏转区,速度降至12.4 m/s。随着滑坡大部分岩土体经过沟道偏转区,滑坡岩土体运动到相对宽阔平坦的地形,在摩擦和碰撞的因素作用下速度逐渐减小,在大约80 s时,滑坡岩土体停止堆积,滑坡运动结束。
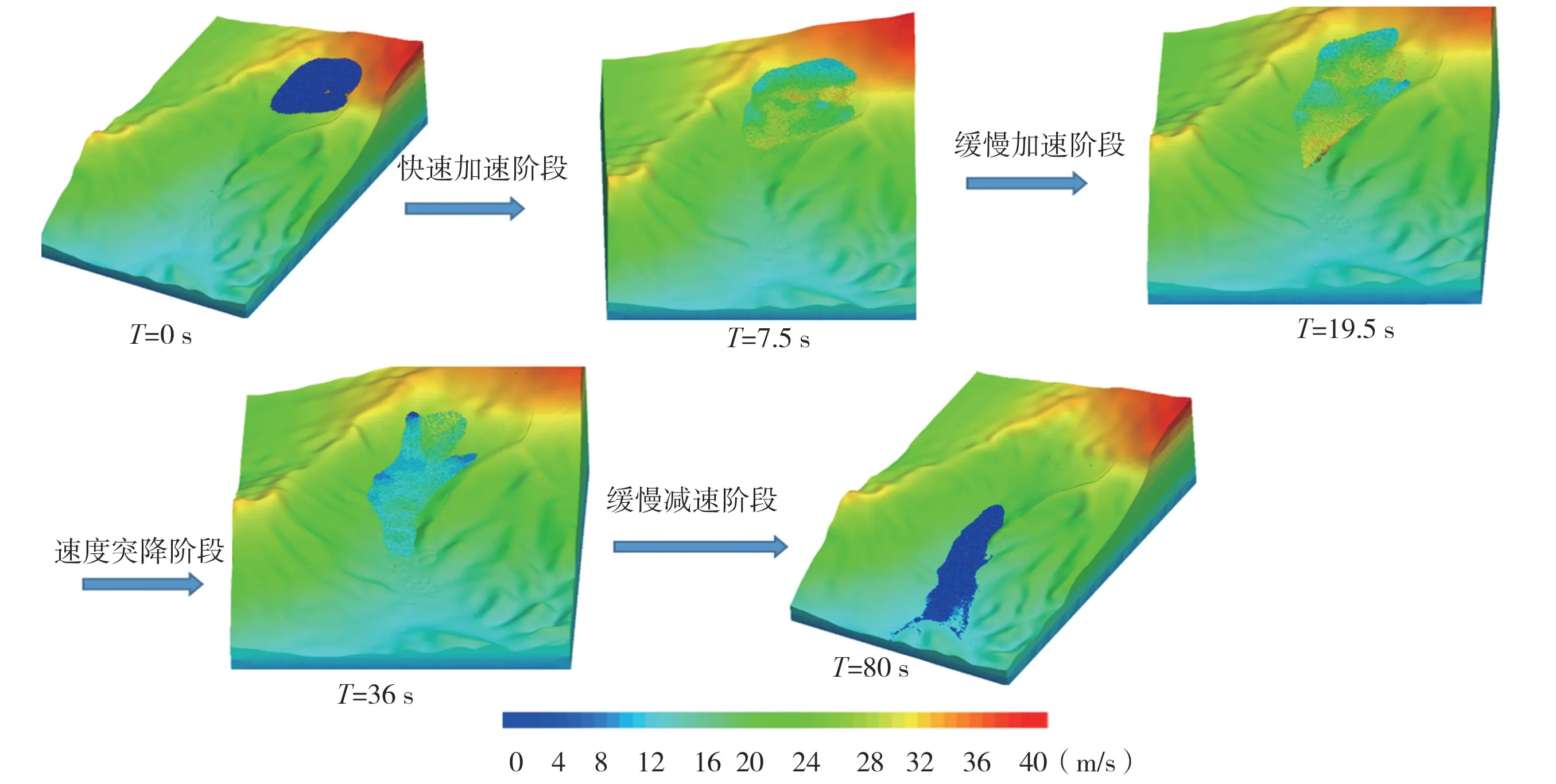
图8 滑坡运动演化过程Fig.8 The evolution process of landslide
受地形条件的作用,三溪村滑坡前缘岩土体运动速度呈现一定的差异(图9)。在开始阶段,前缘岩土体运动基本一致,即滑坡失稳后,经过陡坎阶段速度快速增加,到达偏转区时速度增加至峰值速度,由于岩土体和偏转区山体激烈碰撞,岩土体破碎解体继续向前运动并逐渐停止堆积。其中前缘左侧岩土体运动距离<前缘右侧岩土体运动距离<前缘中部岩土体运动距离,这是因为滑坡启动后前缘左侧岩土体不在主滑方向上,而是向主滑方向运动,在运动过程中和中部岩土体碰撞,能量耗散较多,呈现出运动距离最短的现象。而前缘右侧岩土体运动到偏转区时,和山体激烈碰撞、摩擦,造成滑坡动能大量耗散,致使运动距离小于中部岩土体运动距离。
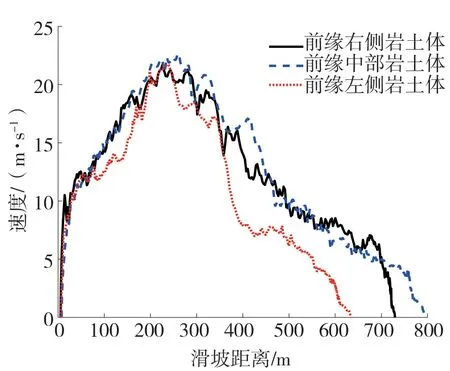
图9 滑坡沿程速度演化曲线Fig.9 The velocity evolution curve of landslide
三溪村滑坡前缘各部位岩土体速度曲线也呈现一定的差异(图10),右侧岩土体峰值速度为21.05 m/s,中部岩土体峰值速度为22.68 m/s,左侧岩土体峰值速度为21.75 m/s。前缘岩土体速度均是先增加后减小至0,但前缘岩土体各部位速度变化不相同。滑坡前缘各部位岩土体速度的差异主要受地形和主滑方向改变的影响,结合图4可以看到三溪村滑坡前缘开阔,滑坡启动后,受重力势能和后部岩土体的推挤作用,前缘岩土体速度持续增加,前缘岩土体到达陡坎地带,受到重力势能的影响,岩土体速度急速增加并向前冲击。滑坡岩土体运动到狭窄的沟谷地带后,受到沟谷地形条件的影响,岩土体和沟谷两侧山体、岩土体之间撞击、摩擦加剧,导致岩土体速度增加幅度降低。滑坡岩土体运动到偏转区时,受到偏转地形条件的影响,前缘岩土体和右侧山体激烈碰撞致使岩土体破碎解体,由于激烈的碰撞和摩擦,滑坡速度减小,主滑方向发生改变。滑坡岩土体运动到堆积区后,滑坡进入最后的减速阶段,岩土体颗粒与地面持续发生摩擦,滑坡前缘速度持续减小,滑坡前缘陆续堆积在堆积区,后部分岩土体撞击并铲刮堆积区岩土体使得滑坡速度进一步减小直至停止。
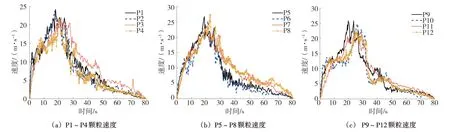
图10 前部岩土体颗粒速度Fig.10 The velocity of the front rock mass
运用加速度随时间的变化曲线进一步揭示了滑坡速度变化规律(图11)。如图11所示,3个部位岩土体加速度变化趋势大致相同,都是先由正向负变化直至停止运动。即滑坡启动初始阶段加速度最大,呈现为快速加速阶段,后受地形条件和摩擦的影响,加速度逐渐减小至0,随着滑坡岩土体运动到偏转区,岩土体破碎解体,滑坡前缘速度减小,加速度变为负值,且随着碰撞加剧,加速度向着负方向增加至最大值,后因受到地面摩擦和铲刮作用,滑坡加速度逐渐减小直至停止运动。
结合三溪村滑坡前缘运动速度和加速度分布演化特征,三溪村滑坡前缘速度分为4个阶段,即快速加速阶段、缓慢加速阶段、速度突降阶段、缓慢减速阶段。下文逐一介绍各阶段速度变化情况:
(1)快速加速阶段:运用滑坡前缘岩土体速度曲线进一步揭示滑坡速度变化规律(图12),如图12所示,滑坡岩土体右侧快速加速阶段持续时间最短为1.91 s,中部岩土体快速加速阶段持续时间为5.39 s,左侧岩土体快速加速阶段持续时间为7.31 s。且由图11加速度曲线可知三溪村前缘右侧岩土体初始阶段加速度最大,其次是中部岩土体加速度,左侧岩土体加速度最小。作者认为其原因在于以下2个方面,滑坡启动后左侧岩土体受到左边突出山体的挤压和碰撞,启动和下落受到限制,而右侧岩土体处在比较平坦的地形条件之下,启动和下落受限制较小,即呈现出在较短的时间内速度迅速增大。三溪村滑坡主滑方向的改变是影响前缘各部位岩土体快速加速阶段不同的主要因素,右侧岩土体运动方向为主滑方向,而中部和左侧岩土体在初始阶段是向主滑方向运动,运动过程中和右侧岩土体碰撞,导致初始阶段右侧岩土体加速度>中部岩土体加速度>左侧岩土体加速度。
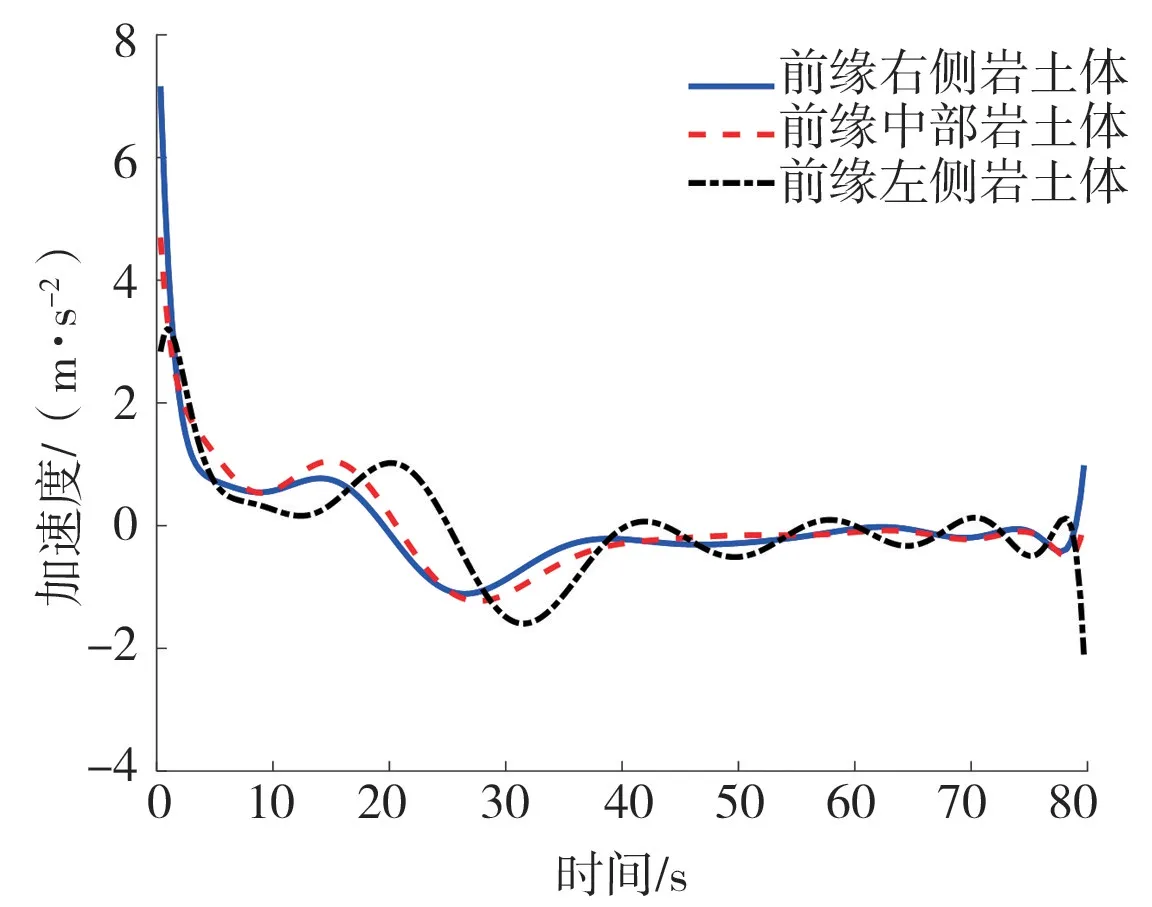
图11 前缘岩土体颗粒加速度Fig.11 The acceleration of the front rock mass
(2)缓慢加速阶段:观察图12可以看出,滑坡前缘岩土体缓慢加速阶段持续时间不同,其中右侧岩土体缓慢加速阶段持续时间为18.89 s,中部岩土体缓慢加速阶段持续时间为15.81 s,左侧岩土体缓慢加速阶段持续时间为19.09 s,前缘岩土体在地形条件的影响下,加速度逐渐减小。中部岩土体的峰值速度最大,其原因在于中部岩土体处于主滑方向上,受两侧山体凸出地形条件的影响小。
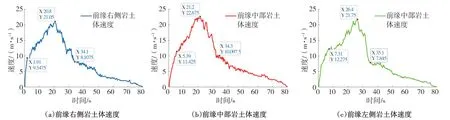
图12 前缘岩土体速度Fig.12 The velocity of the front rock mass
(3)速度突降阶段:右侧岩土体速度突降阶段持续时间为13.3 s,中部岩土体速度突降阶段持续时间为13.1 s,左侧岩土体速度突降阶段持续时间为8.7 s。岩土体受到摩擦和碰撞的作用导致速度快速降低。为了更好的研究三溪村前缘岩土体减速阶段运动过程,对减速阶段进行拟合(图13),右侧岩土体减速阶段呈现出规律性的减速过程,而中部和左侧岩土体减速阶段则呈现出明显的速度突降和缓慢减速过程。其中左侧岩土体速度突降阶段斜率>中部岩土体斜率>右侧岩土体斜率。这是因为左侧岩土体进入沟谷地形时,受到偏转地形的影响,滑动方向改变幅度较大,如图4,主滑方向由57°改变为350°,造成左侧岩土体颗粒和中部岩土体激烈碰撞,致使左侧岩土体迅速减速。相关的沟谷偏转型滑坡的模型试验[22]显示了滑坡体速度在偏转位置处发生突变。
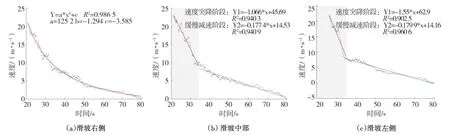
图13 滑坡减速阶段拟合Fig.13 Fitting of debris flow deceleration stage of landslide
(4)缓慢减速阶段:滑坡岩土体运动到堆积区,在摩擦和碰撞的影响下,岩土体逐渐减速直至停止堆积。当滑坡岩土体运动到堆积区,进入缓慢减速阶段,右侧、中部、左侧岩土体共同运动到开阔地带,其缓慢减速阶段加速度变化相似。
4 三溪村滑坡对山区房屋的冲击力特征
为研究滑坡对山区建筑的冲击作用机制,采用冲击力作为量化指标,建立4处房屋的冲击力时程关系(图14),分析滑坡运动堆积区房屋遭受滑坡冲击的致灾机制。本研究利用PFC将需监测的房屋受冲击面设置为“刚性wall”,利用PFC遍历颗粒与“wall”的接触,获得该位置的冲击力曲线。虽然山区农房结构存在不同差异,但房屋尺寸和灾难性滑坡的规模相比是极小值,文中主要研究的是冲击力的时程和运程的分布,不开展房屋结构的损坏机制研究,因此不考虑房屋结构的影响,因此本文选择在房屋所在位置处,将房屋简化为挡墙的形式,进行冲击力的提取与研究。得到冲击力时程曲线(图15)。图15中,房屋离滑源区距离越远,其遭受的滑坡峰值冲击力越小。房屋遭受滑坡冲击可以分为三个阶段即冲击力陡增阶段、冲击力下降阶段和准静态堆积阶段。1、2、3号房屋冲击力变化形式为先增大至峰值冲击力再减小至残余冲击力,4号房屋冲击力变化形式为从零开始逐渐增加至残余冲击力。其原因是4号房屋处于滑坡运动逐渐堆积的位置,当滑坡岩土体运动到此处,其运动速度较小,对房屋建筑的动态冲击作用较小,而随着滑坡岩土体逐渐堆积在房屋建筑周围,其对房屋建筑作用的静态堆积力逐渐增加。而1、2、3号房屋位于滑坡运动堆积阶段,即房屋先遭受滑坡的动态冲击,随着滑坡岩土体逐渐堆积在房屋周围,其遭受的冲击力形式由动态冲击阶段转变为准静态堆积阶段。用Fmax1、Fmax2、Fmax3、Fmax4分别表示1号房屋~4号房屋的峰值冲击力,F1、F2、F3、F4分别表示1号房屋~4号房屋的残余冲击力,其中Fmax1>Fmax2>Fmax3>Fmax4,F2>F3>F4>F1,对比残余冲击力可以看出1号房屋残余冲击力最小,这是因为1号房屋位于堆积区后缘,堆积的岩土体较少,而2,3,4号房屋位于滑坡堆积区前缘,堆积的岩土体较多。

图14 房屋位置Fig.14 The location of the building
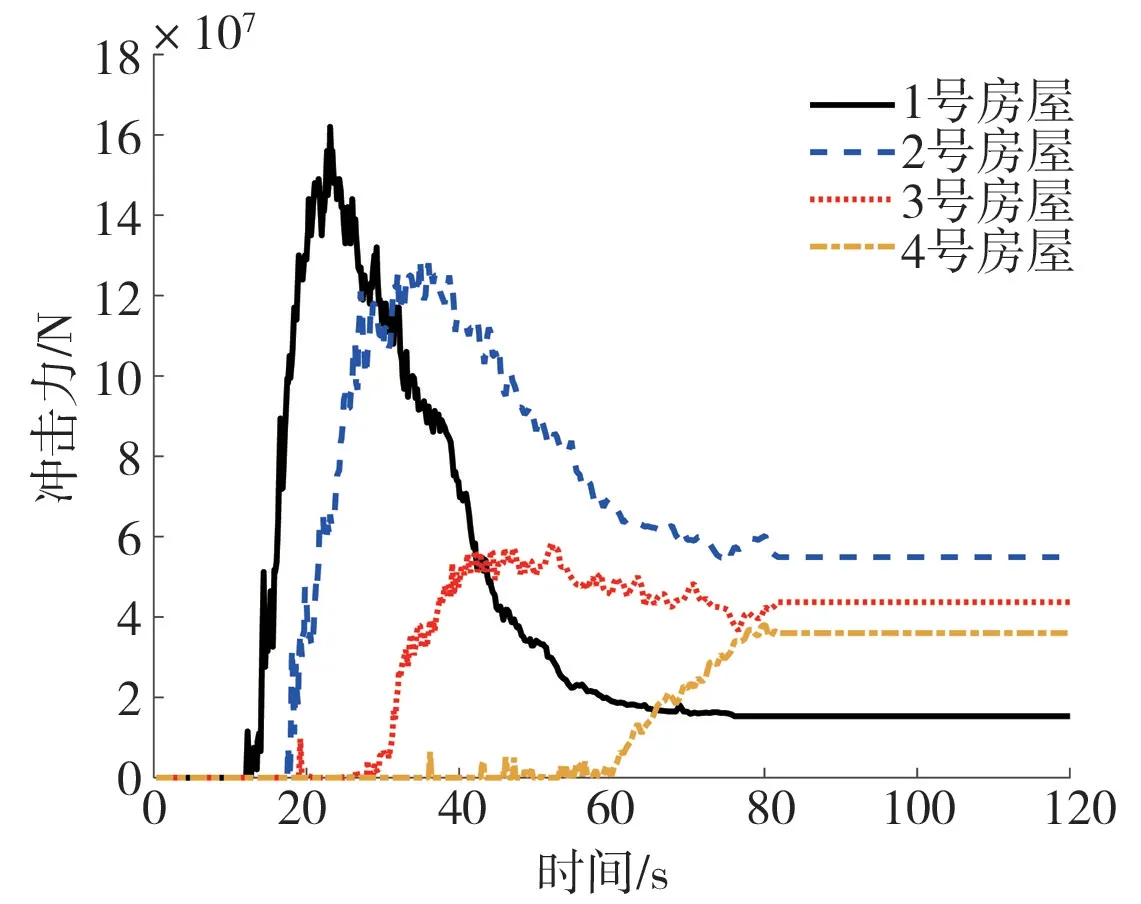
图15 房屋冲击力时程曲线Fig.15 Time history curve of building impact force
从冲击力增加阶段来看,1号房屋斜率>2号房屋斜率>3号房屋斜率>4号房屋斜率,冲击力下降阶段中1号房屋斜率>2号房屋斜率>3号房屋斜率>4号房屋斜率,滑坡前缘开始冲击1号房屋时速度为15.4 m/s,三溪村滑坡在1号房屋处达到峰值冲击力时刻的速度为23.1 m/s(表2),即是1号房屋位于滑坡加速阶段,滑坡加速通过1号房屋致使1号房屋受到的冲击力急速增加,并且三溪村滑坡在1号房屋周围堆积较少,致使1号房屋受到的冲击力在短时间内快速下降。而2、3、4号房屋位于滑坡减速阶段,呈现出滑坡在冲击房屋的过程中,随着速度的降低,部分岩土体逐渐堆积在房屋周围,滑坡冲击力缓慢下降,呈现出准静态堆积阶段。

表2 冲击力与速度Table 2 Impact force and velocity
由上面分析可知,山区建筑遭受滑坡冲击,产生的峰值冲击力和山区建筑离滑源区的距离存在联系,为进一步研究山区建筑物遭受峰值冲击力和其位置的关系,文中以1号房屋为初始点按40 m的间距设置11个监测点得到峰值冲击力和距离的关系(图16)。由图16得到,监测点到滑源区距离越远,峰值冲击力逐渐减小,0~50 m阶段随着距离的增加,冲击力下降的较快,其后随着距离的增加,冲击力下降较慢,这是因为三溪村滑坡的特殊地形造成的,在滑坡启动后岩土体激烈冲击右侧山体,使得滑坡方向偏转,岩土体以碎屑流的形式继续向前运动,三溪村滑坡在这一阶段能量损失较大,岩土体能量和速度变化较大,造成在这一阶段房屋遭受滑坡的冲击力变化幅度较大。在滑坡堆积区处,房屋遭受的峰值冲击力受距离的影响较小。这是因为随着滑坡运动速度逐渐减小,滑坡岩土体逐渐堆积在房屋周围,房屋遭受的动态冲击作用很小,静态堆积作用占据主导。
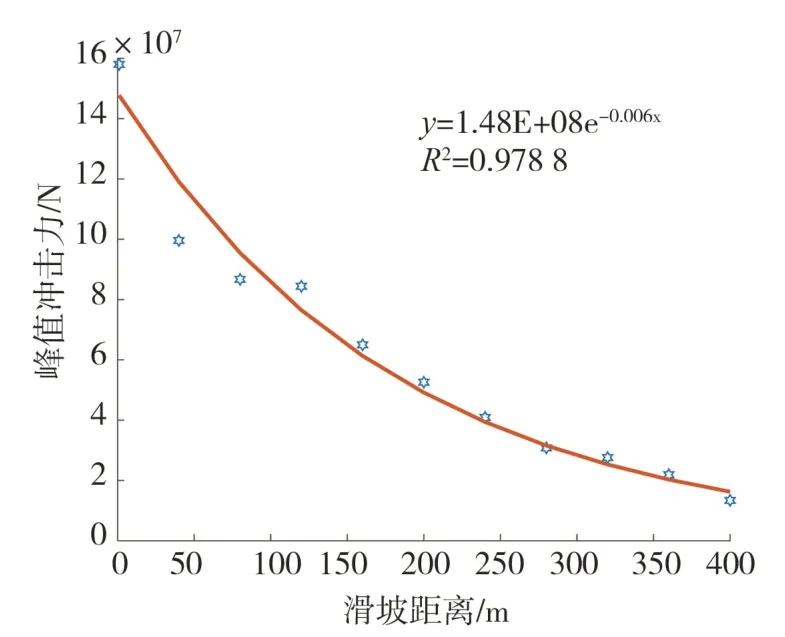
图16 峰值冲击力与运程曲线Fig.16 Peak impact force and distance curve
利用峰值冲击力与速度关系曲线进一步揭示速度对峰值冲击力的影响(图17),如图17,随着滑坡速度的减小,滑坡对房屋产生的峰值冲击力逐渐减小,当速度较大时,滑坡对房屋产生的冲击力受速度的影响较大,而当速度较小的时,滑坡对房屋产生的冲击力受速度的影响较小,由此可见滑坡速度是影响滑坡对房屋建筑峰值冲击力的主要因素。
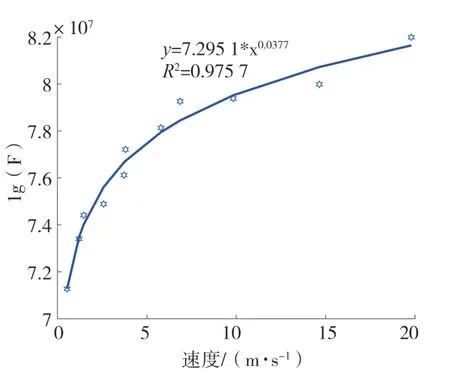
图17 峰值冲击力与速度曲线Fig.17 Peak impact force and velocity curve
5 结论
本研究利用三维离散元软件PFC3D,对三溪村滑坡进行模拟,取得了较好的效果。特别是对于前缘颗粒速度变化、滑坡冲击力研究取得了较好的结果。通过对三溪村滑坡进行数值模拟得到以下结论:
(1)三溪村滑坡启动后前缘岩土体在重力势能和后缘岩土体的推挤作用下,沿着沟谷地形快速向下滑动,三溪村滑坡前缘开阔,致使滑坡初期岩土体速度快速增加并向下滑动,通过监测前缘速度发现,前缘岩土体由于能量传递、碰撞、推挤,呈现出不同的速度变化。其中偏转地形造成主滑方向的改变,是影响滑坡运动的主要因素,受到偏转区的影响,滑坡前缘各部位速度变化各不相同,滑坡初期前缘右侧岩土体加速度最大,在加速阶段中,中部岩土体呈现出最大的峰值速度,在急减速阶段中,左侧岩土体加速度最大。
(2)根据滑坡前缘岩土体运动速度和加速度分布演化特征,三溪村高速远程滑坡的运动过程可划分为四个阶段,即快速加速阶段、缓慢加速阶段、速度突降阶段、缓慢减速阶段。
(3)通过对冲击力的研究发现,房屋遭受滑坡冲击主要分为3个阶段即冲击力陡增阶段、冲击力下降阶段和准静态堆积阶段,滑坡启动后岩土体持续冲击山区建筑,在动能的作用下,滑坡冲击力急剧增大至峰值,而随着滑坡继续向前运动至停止,房屋遭受滑坡动态冲击阶段结束,部分岩土体堆积在房屋周围并持续给房屋施加“静态冲击力”,使得冲击力曲线呈现出准静态堆积。
(4)建立的冲击力运程曲线显示,滑坡冲击山区建筑,产生的峰值冲击力和山区建筑位置相关,房屋到滑源区距离越远,峰值冲击力越小。当房屋离滑源区近时,房屋遭受峰值冲击力随着距离的变化幅度较大,而当房屋离滑源区较远时,房屋遭受峰值冲击力随着距离的变化幅度较小。当速度较大时,滑坡对房屋产生的冲击力受速度的影响较大,而当速度较小时,滑坡对房屋产生的冲击力受速度的影响较小。

