基于CRITIC法与TOPSIS地铁车站施工安全评价

胥 明，许 杰，万友生，覃 君，吴 波，谢云杰

（1.南昌轨道交通集团有限公司，江西南昌 330038；2.广西大学土木建筑工程学院，广西南宁 530004；3.中铁二局第六工程有限公司，四川成都 610036）

引言

随着我国经济的发展和城市人口的剧增，越来越多的城市兴建地铁以缓解日益增长的交通压力。地铁车站一般修建在城市繁华地区，且具有“深、大、近、难”的特征［1］，往往遇到周边环境复杂的情况：工程地质条件复杂、施工范围内管线众多、周围房屋密集、交通繁忙、周围居民较多，造成不确定因素多，风险大，施工困难的问题，需要对地铁车站施工安全做出科学合理的评价。

地铁车站施工安全评价一般使用的方法为故障树法、模糊理论、熵权法、灰色关联度法、层次分析法和其他方法［2］。薛模美等［3］、周红波等［4］采用故障树法对基坑施工风险进行分析，得出施工各阶段的风险等级与风险控制措施。Guohua Zhang等［5］、李朝阳等［6］、吴波等［7］基于模糊理论确定施工风险因素的权重，建立了深基坑风险评估体系。Zhenhua Luo等［8］、陈蓉芳等［9］、王景春等［10］利用熵权法对评价指标进行加权处理，构建地铁深基坑的风险评价体系。郎秋玲等［11］利用现场数据和灰色关联度法建立评价模型，对地铁深基坑开挖稳定安全性进行评价。Yuanshun Shen等［12］、李凤伟等［13］、聂菁等［14］采用层次分析法对地铁车站风险元素进行排序，进行安全风险分析。Ping Liu等［15］使用粒子群优化算法（PSO）的支持向量机（SVM）模型，对地铁车站施工的安全风险进行预测。Luyuan Wu等［16］将网络分析法（ANP）和模糊综合评判法（FCE）结合，可对地铁车站总风险等级进行评价。顾雷雨等［17］基于风险概率统计分析的理论，对复杂环境中基坑施工安全预警标准研究，提出了一种预警标准设计方法。姜安民等［18］基于突变级数法构建了地铁车站施工风险预测模型。上述方法虽能较好地对地铁车站基坑施工安全评价，但是却均有一些局限性，如故障树法计算复杂，且需事先知道所有基本事件发生的概率，否则无法进行定量分析；模糊综合评判法对指标权重矢量的确定主观性较强，结果可能会出现超模糊现象，分辨率差；熵权法仅依靠数据分析，客观性过强，计算结果常与工程实际有较大的偏差，无法体现决策者对各个安全评价指标的重视程度；灰色关联度法无法解决评价指标间相关造成的评价信息重复问题，对指标的最优值难以确定；层次分析法和模糊层次分析法过于依赖决策者的主观判断，可能受到主观偏好的不利影响。

由此可见，国内外在分析复杂环境地铁车站施工安全性的研究较少，如何综合考虑安全评价指标的主、客观性，对其量化并确定权重是进行安全评价的关键。文中将CRITIC法与TOPSIS理论结合，综合考虑安全评价指标的主、客观性，并能将安全评价结果量化，形成一套地铁车站施工安全评价模型：CRITIC法可以综合评价指标间的对比强度与冲突性，对评价指标进行客观赋权，将CRITIC法与TOPSIS理论相结合，可以克服采用传统的定性分析或经验模糊数学理论存在主观性大、可靠性不高的缺点，而TOPSIS理论则可以对多评价指标进行合理排序、综合决策并求得具体的隶属度。经实例验证，将CRITIC法与TOPSIS理论两者结合能在地铁车站施工安全评价中得到较好的应用，评价结果较科学、准确，符合工程实际。

1 地铁车站施工安全评价流程

1.1 安全评价指标体系

根据地铁车站施工情况和事故发生的机理，依据相关法律法规［19］和相关文献［20－24］，参考行业专家意见与类似工程案例，对地铁车站安全性评估系统进行全面分析，建立一套科学合理、操作性强的安全指标体系：建立4个二级指标，20个三级指标，如图1所示。

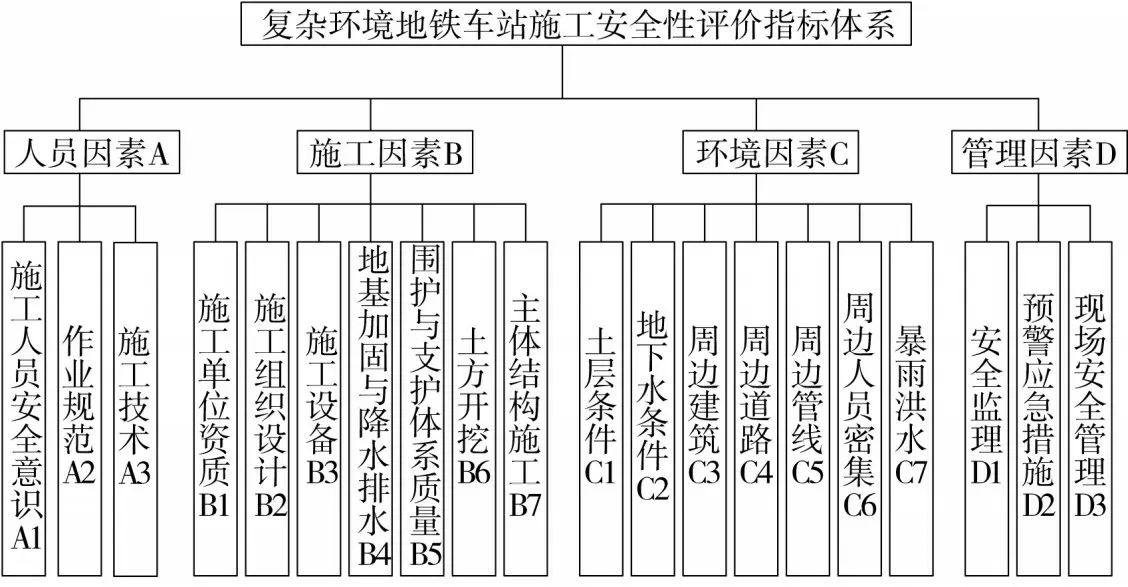
图1 地铁车站施工安全性评价指标体系Fig.1 Safety evaluation index system for subway station construction in complex environment

为保证评价指标的一致性，结合概率论理论和专家评分习惯，参照相关规范标准［25］中风险发生可能性与损失等级，将地铁车站施工安全等级和安全性接受准则划分为5个级别，并按［0，1］区间取值，数值越大表示安全性越高，数值越小表示安全性越低，如表1和表2所示。

表1 地铁车站施工安全等级Table 1 Safety level of subway station construction

表2 地铁车站施工安全接受准则Table 2 Safety acceptance criteria of subway station construction

根据相关规范标准［25］与相关文献［22，27－28］，可以得到三级安全评价指标的量化范围，如表3所示。

表3 地铁车站施工安全指标量化范围Table 3 Quantitative scope of construction safety index for subway station

1.2 构建评价矩阵

为综合考虑决策者对各个安全评价指标的重视程度，根据已建立的安全评价指标体系，邀请专家小组对评价指标进行量化打分，取专家评分平均值构成矩阵S1，将此专家评分结果用于构成评价矩阵，步骤如下：

（1）将各专家对每个评价指标的赋值平均，建立一组评价矩阵S1；

（2）将表示专家主观因素的评价矩阵S1与表示指标客观因素的地铁车站施工安全等级节点构成评价决策矩阵D；

（3）将评价决策矩阵进行标准化，并通过初等变换得到标准化评价决策矩阵Q，标准化评价决策矩阵Q是CRITIC法综合赋权的基础矩阵。

1.3 CRITIC法综合赋权

Diakoulaki提出CRITIC法，该方法用于处理多属性决策的综合赋权问题，将CRITIC法应用于安全评价时，可对多个安全评价指标进行综合赋权，不仅能考虑安全评价指标间的对比强度，更能考虑其冲突性，综合衡量评价指标的客观权重［29］。

CRITIC法计算评价指标组合权重步骤如下：D=（dij）m×n为评价决策矩阵，d ij为评价矩阵S1的元素与地铁车站施工安全等级节点共同组成，若原始评价指标的量纲和数量级不一致，为消除其影响，需对其进行标准化处理，得到标准化评价决策矩阵Q，再求出评价指标间的相关系数rtj，构建相关系数矩阵R=（rtj）m×n，其中rtj为：

求各评估属性的信息量与权重。各评价指标的客观权重以评价指标间的对比强度和冲突性来综合衡量，设Cj表示第j个评价指标所包含的信息量：

σj为第j个评价指标的标准差，rtj为评价指标间的相关系数。CRITIC法的客观性通过评价指标间的对比强度与冲突性来体现，其中对比强度表示同一个评价指标各在各方案中取值差距的大小，以标准差的形式来表现，标准差越大，说明该评价指标在各方案之间的差距越大，数据反映的信息量越大；冲突性是以评价指标间的相关性为基础，计算评价指标间的冲突性，如2个评价指标存在较强的正相关，则这2个指标冲突性较低［29］。式（1）体现了CRITIC法的赋权综合了评价指标的对比强度与冲突性，显然Cj越大，第j个评价指标所包含的信息量越大，该指标的相对重要性也就越大，故权重wj为：

构建标准化加权评价决策矩阵V=（vij）m×n。

1.4 TOPSIS理论

1981年C.L.Hwang和K.P.Yoon提出了一种解决单一型或混合型多评价指标决策问题的方法——逼近理想解排序方法TOPSIS（Technique for Order Preference by Similarity to Solution）［31－32］，其具有易于理解、计算简单、适用范围广、几何意义直观、结果合理等优点［33］。将TOPSIS应用于安全评价中，具有以下优点：TOPSIS理论则可以对多评价指标进行合理排序、综合决策，并求得评价指标具体的隶属度。但该方法需要评价指标的量化数据，且采用各方案与理想解和负理想解的距离来计算，故受指标的离散程度影响较大。故文中将其与CRITIC法相结合，以减小上述不足，使其可应用于地铁车站施工安全评价。

TOPSIS计算原理为：基于标准化加权评价决策矩阵，定义多评价指标决策问题的正理想解和负理想解，分别计算各方案与理想解和负理想解的距离，然后计算各方案的综合评价值（即各评价方案与最优方案的相对接近距离），最后根据综合评价值对各方案进行排序。综合评价指标距离正理想解越近，而距离负理想解越远，评价结果越优，其方案越好。具体计算如下：

基于标准化加权评价决策矩阵，计算正理想解V+和负理想解V－。

计算各方案的相对贴近度。

1.5 安全评价流程图

将CRITIC法与TOPSIS结合用于评价地铁车站施工安全评价主要流程如下：首先根据安全评价体系，邀请业内专家对评价工程按评价指标进行打分，再将专家打分结果与安全等级节点构成评价决策矩阵，利用CRITIC法综合考虑主、客观因素，计算指标权重，再采用TOPSIS计算评价指标具体的隶属度，确定施工安全等级，最后根据评价结果，参考安全接受准则，实施相应的安全对策，安全评价流程如图2所示。

图2 地铁车站施工安全评价流程图Fig.2 Flow chart of construction safety assessment of subway station

2 案例分析

2.1 工程概况

施尧站为南昌市轨道交通3号线工程的第8座车站，车站位于江铃六路与迎宾北大道交汇处，车站总长约197.6 m，标准段宽22.7 m，端头井处宽26.8 m，底板埋深约为16.7 m，端头井处底板埋深约为18.1 m。本车站采用半盖挖法施工，车站主体围护结构采用800 mm地下连续墙，内设3道支撑，第一道为钢筋混凝土支撑，支撑一端与冠梁连接，另一端与盖板纵向连系梁连接，第二道至第三道支撑为钢支撑，在连系梁位置用钢筋抱箍固定并预加轴力。车站标准断面图如图3所示。

图3 地铁车站标准断面图Fig.3 Standard section of the subway station

施尧站位于赣抚冲积平原区的二级阶地，地处鄱阳湖滨湖前后缘地带，地表水系发育，且降雨量多集中在4～6月，约占全年降雨量的51%，常有暴雨洪涝灾害。地层自上而下依次为0.6～0.7 m厚的杂填土、0.6～4.0 m厚的素填土、0.8～7.8 m厚的粉质黏土、2.0～11.5 m厚的中砂、1.4～7.5 m厚的粗砂、4.5～12.2 m厚的砾砂、圆砾、0.5～1.2 m厚的强风化泥质粉砂岩、往下为中风化泥质粉砂岩和钙质泥岩。

场地周边环境主要为居民区、城市道路，道路两边地下管线复杂。车站周边建筑有汽车玻璃厂（距车站约10 m）、超市（距车站约11 m）、药房（距车站约14 m）、医院综合楼（距车站约16 m）等，建筑较多、较近和密集；周边城市道路主要为双向4车道的迎宾北大道和江铃六路；周边管线多且密集，见表4。

表4 地铁车站管线情况Table 4 Pipeline condition of subway station

2.2 确定评价指标权重

根据已建立的安全评价指标体系，邀请5位专家对评价指标进行量化打分，评分情况汇总于表5。

表5 专家小组评分汇总表Table 5 Summary table of expert panel scores

将代表主观因素的专家评分平均值与代表客观因素的安全等级节点构建评价决策矩阵，并进行标准化处理，得到标准化评价决策矩阵Q如下。

利用CRITIC法可计算得各评价指标的权重如表6所示。

表6 评价指标权重Table 6 Weight of evaluation index

由此可知，三级评价指标中最重要是C3（周边建筑）、C6（周边人员密集）、C5（周边管线），二级评价指标的重要性排序为C＞B＞A＞D。

根据CRITIC法计算得到的客观权重，分别将此权重赋予标准化决策矩阵Q，可以得到标准化加权决策矩阵I。

2.3 地铁车站安全性评价

依据图1所示的地铁车站施工安全评价指标体系和通过CRITIC法得到的标准化加权决策矩阵Q，利用TOPSIS理论进行安全性评价。利用式（8）、（9）计算各指标到正理想解和负理想解距离、，对评价指标进行综合决策，利用式（10）计算相对贴近度C*i，进行合理排序，结果如表7所示。

表7 各评价指标的距离及相对贴近度Table 7 The distance and relative closeness of each evaluation index

二级评价指标人员、施工、环境、管理的隶属度分别为：0.550、0.605、0.504、0.572，其中人员、环境、管理均对应于安全接受准则Ⅲ级，即安全性中等，施工对应于安全接受准则Ⅱ级，即安全性较高。

2.4 多种方法对比分析

为验证本文方法的准确性与实用性，分别采用层次分析法和灰色关联度法，对本地铁车站施工安全性进行评价，其中灰色关联度无法计算权重，故采用1/n权重和CRITIC法权重分别计算，限于篇幅此2种方法计算过程不做具体说明。所得结果如图4所示，其中方法1为层次分析法计算结果，方法2为1/n权重的灰色关联度法计算结果，方法3为CRITIC法权重的灰色关联度计算结果，方法4为本文CRITIC法－TOPSIS计算结果。

图4 多种方法对比分析结果Fig.4 Comparison and analysis of results by multiple methods

由图4可得：层次分析法确实过度依赖决策者的主观判断，导致各二级评价指标差异过大，对人员、施工、管理的安全评价过于冒险。灰色关联度法存在无法计算评价指标权重的缺陷，需与其他权重计算方法结合使用，当采用CRITIC法权重计算所得隶属度与本文方法大致相同，但确实可能存在前文所提的超模糊现象，分辨率差的问题，如人员指标与施工指标、环境指标与管理指标的隶属度大小较接近，结果无法很好地区分。文中的CRITIC法结合TOPSIS进行地铁施工安全评价，所得结果与本工程验收专家得出的结果一致，与该复杂环地铁车站的实际情况相符，且综合考虑了评价指标的主、客观因素，不会过分依赖决策者的主观判断，不存在分辨率差的问题，由此可见本方法是可行且较准确的。

3 地铁车站施工安全措施分析

根据上述地铁车站施工安全性分析，结合施尧站实际情况，得出以下安全措施与施工建议。

（1）通过上述安全性评价结果可知：指标人员、施工、环境、管理的隶属度分别为：0.550、0.605、0.504、0.572，其中环境的安全性最低，因此在施工过程中需要加强对周边复杂环境的安全管控，否则一旦发生安全事故，将会在很大范围内造成人员伤亡与财产损失。

（2）在施尧站施工中，周边环境的权重占46.03%，且其安全性程度最低。为保证复杂周边环境地铁车站的施工安全，可采取以下措施：1）由于地层为富水砂层，且地下水丰富，因此要做好基坑降水工作，承压水必须控制到确保不发生基底管涌的水位以下；2）加强周边道路、建筑、管线的监控量测，用监测数据指导施工，特别是对距离基坑较近的重要管线，可以迁移的尽量迁移，对于不能迁移的管线，应对其变形进行监测，保证不会因基坑施工而破坏；3）开挖基坑是引起道路、建筑、管线等变形的主要原因，在施工过程中，尽量缩短围护结构暴露时间，土方开挖满足混凝土结构施作条件后，立即展开混凝土结构的施工。

（3）二级指标人员与施工安全性评价为中等，因此需要对施工人员进行相应的技术培训与安全培训，保证其施工作业规范。在土方开挖、围护结构、主体结构等施工过程中，应注意施工工序的合理规范。

4 结论

文中采用CRITIC法与TOPSIS理论，依托南昌轨道交通3号线施尧站项目，对地铁车站施工进行安全性评价，主要结论如下：

（1）考虑工程实际的不确定性和复杂性，在调研国内外相关学者研究的基础上，较完整合理地建立了地铁车站施工安全性评价指标体系。将影响地铁车站施工的安全性因素划分为人员因素、环境因素、施工因素和管理因素，再细分为20个三级指标，既把握全面又突出重点，能为类似工程项目安全评价提供参考。

（2）在影响地铁车站施工安全的人员、环境、施工和环境因素中，采用CRITIC法对其进行权重分析，可知环境的权重较大，且环境的安全评价指标较小，原因是施工现场的建筑、道路、管线等因素对施工安全影响很大，因此在施工过程中，需要对周边环境给予足够的重视，采取相应保护措施是十分重要的。

（3）将CRITIC法与TOPSIS理论有效结合，建立了地铁车站施工安全评价模型：采用CRITIC对各安全性评价指标进行客观赋权，再利用TOPSIS理论计算本工程的安全评价等级为Ⅲ级，安全性为中等，复杂的环境是导致本工程安全性较低的主要因素，与工程实际情况一致，证明了本评价模型是合理适用的，可为类似具有复杂环境的工程提供一种科学合理的安全性评价方法，为后续施工安全保证提供理论支持。