低盒形拉深零件展开尺寸的计算

◇重庆航天职业技术学院 吴 飞

拉深零件的展开尺寸对工厂的制作成本有重大影响。本文先说明了圆筒形拉深零件的展开尺寸的计算方法。在此基础上，又分析了低盒形拉深零件的展开计算方法，并用实例加以说明。

1 序言

拉深成形（又叫压延成形）是钣金工艺中的核心技术之一。它是将平的板料（或空心半成品）利用拉深模压制成一个开口的空心零件。一般的有底筒类零件和盒类零件都是通过拉深成形来制造的。

拉深零件的展开尺寸的计算，对于保证零件的质量和精度，降低制造成本都起着非常重要的作用。

2 预备知识：筒形零件展开尺寸的计算方法

要弄清低盒形零件的展开尺寸的计算方法，必须先弄清圆筒形零件的展开尺寸的计算方法。因为低盒形零件的拐角处圆角的展开，是被当成四分之一个圆筒来处理的。

筒形零件的展开图尺寸计算的原则是：展开图的形状是圆形，展开图的面积等于筒形零件的表面积（不计板厚）

如图1所示为筒形零件。它的表面可以分为三部份，上部为一圆柱面，中部为一四分之一的圆环面，底部为一圆面。设其表面积分别为f1、f2、f3。则（以下这些公式见文献2、3、4）：

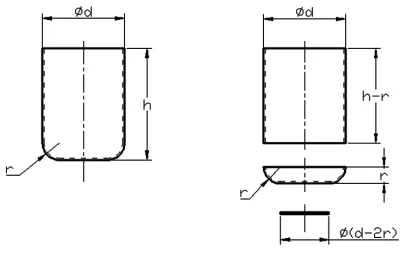
图1 筒形零件及其分解

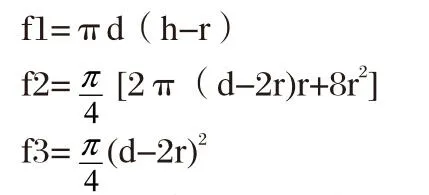
故筒形零件的表面积为

3 低盒形零件展开尺寸的计算

（1）低盒形零件的特点（见图2）。盒形零件的四个拐角部份为四分之一圆筒，其余部分为直边。在拉深时，直边的变形较简单，为弯曲变形。四分之一圆筒的变形则为圆筒的拉深变形。

图2 低盒形零件立体图

低盒形零件一般是指一次就能拉深成形的盒形件，一般情况下，其高度h应小于其短边长度B.其拐角部分的半径r'对拉深成形的影响很大。r’越小，拉深成形越困难，故一次拉深成形的低盒形零件高度h也应越小。

工厂实践表明，对于低碳钢制成的无凸缘的低盒形零件，r'与h的对应关系如下：r'=0.05B,h=(0.26-0.3)B；r'=0.1B,h=(0.45-0.55)B；r'=0.2B,h=(0.7-0.9)B；r'=0.3B,h=(0.85-1.0)B。

（2）展开尺寸的确定。我们的展开方法是：低盒形零件的直边按弯曲零件展开，其四个拐角处按四分之一圆筒形拉深零件展开。这样画出的展开图一般在弯曲与拉深的相接处是不连续的。这时，我们应根据面积不变原理，把它圆整成为平滑连续的曲线。这才是它正常的展开图。

低盒形零件如图3所示，不考虑板厚。它的拐角部分（占整体的四分之一）的展开图的画法如下（见图4）。

图3 低盒形零件三视图

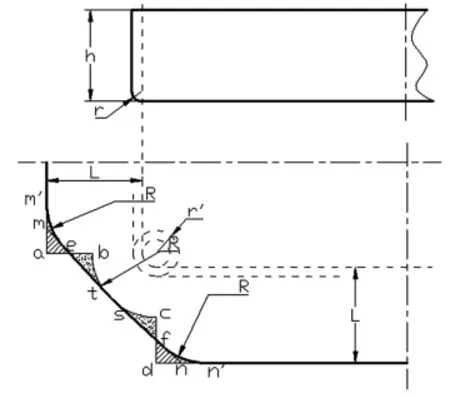
图4 低盒形零件四分之一展开图

a、直边按弯曲零件展开，成一矩形，宽度为L

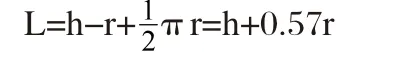
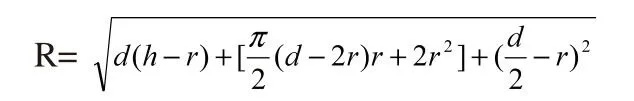
（上式中，d=2r'）

c、画出矩形与扇形连接处的形状曲线abcd。

d、设e,f分别为ab和cd之中点，过e,f分别作圆弧R的切线，切点分别为t,s。切线与展开图的垂直边，水平边之交点分别为m，n。

e、作半径为R的圆弧，分别与展开图左上角及右下角的钝角∠emm'和∠fnn'的两边相切，其中二切点分别为m',n'。

f、平滑曲线m'tsn'就是拐角处的展开图。这是因为去掉的二个曲边三角形之面积等于增加的二个曲边三角形之面积。

实践证明，这种方法确定的毛坯的展开尺寸非常准确。

实例见下：

【例】：已知一低盒形零件之尺寸如图5，求其展开图之尺寸。（图中h=20, B=40, r=2, r'=5）

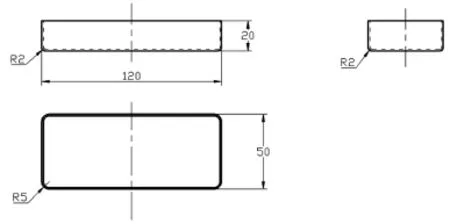
图5 一个具体的低盒形零件

解：此零件的四个拐角中的一个（零件的四分之一）的展开如下（见图6）。

图6 一个具体的低盒形零件四分之一展开图

a、直角弯曲部分展开成一矩形，宽度L为：

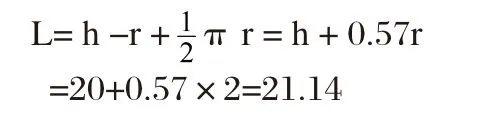
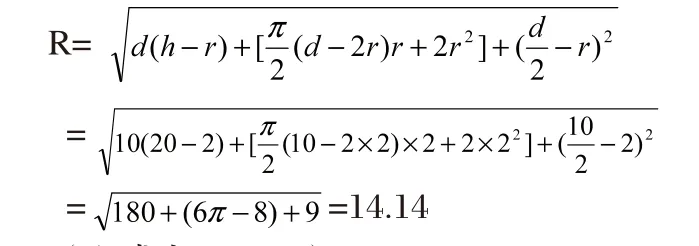
（上式中，d=2r'）

c、画出矩形与扇形连接处的形状曲线abcd。

d、设e，f分别为ab和cd之中点，过e，f分别作圆弧R的切线，切点分别为t,s。切线与展开图的垂直边，水平边之交点分别为m',n'。

e、用半径为R=14.14的圆弧，分别与展开图上的钝角∠tmm'和∠snn'的两边相切，其中二切点分别为m',n'。

f、平滑曲线m'tsn'即为拐角处的展开图。

g、用镜象的方法，即可得到这个低盒形零件的全体展开图（见图7）。

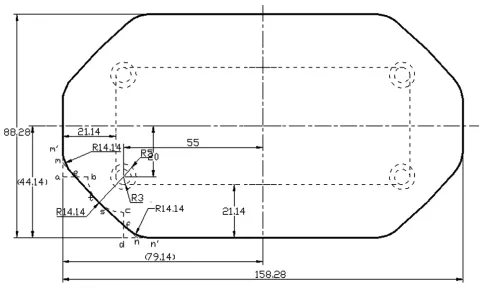
图7 低盒形零件完全展开图