证据理论在模式分类中的应用综述

刘帅彤, 李晓军, 周志杰, 姚俊萍, 王 杰

(火箭军工程大学, 陕西 西安 710025)

0 引 言

近年来，随着互联网和大数据技术的盛行，人工智能，尤其是机器学习和深度学习领域的各种算法得到了不断的创新和发展[1]。模式分类问题及其算法是机器学习与人工智能领域当前发展与研究过程中的热点内容，相关领域的众多学者和研究人员也分别针对不同问题提出了各种方法[2]。然而，在现实生活中，人们所能采集到的信息充斥着大量不确定性，只有在某些特定的条件下才能保证获取到的信息是完备、准确的。在人工智能与模式分类等领域中，往往需要对已知的不完整数据进行处理，最终做出正确有效的判断与决策[3]。

从不确定性信息处理的角度来看，分类结果的不精确甚至不准确很可能是由于样本的属性值不能明确指向某一类，即不同类之间的属性边界通常不精确，甚至重叠[4]。例如，在一个二分类问题当中，有A和B两类，对于某一待分类数据得到的初步分类结果是(0.51,0.49)，即该数据项指向A类别的概率为0.51，指向B类别的概率为0.49，根据常识应该将其归为类别A，但实际上不难看出，两种类别的差距十分相近，类别边界无法区分，此时就会存在有错误分类的风险。因此，不确定性问题的研究对模式分类技术的发展具有至关重要的作用。众多学者们多年以来对于不确定性问题的探究已逐渐形成了各种理论，如概率论[5]、模糊集理论[6]和粗糙集理论[7]等。证据理论作为一种表示和处理不确定性的经典理论，自二十世纪七、八十年代被提出以来，凭借其在不确定性推理方面的优势得到了飞速发展，并被广泛应用于专家系统[8]、故障检测[9]、多属性决策[10]、信息融合[11]和模式分类[12]等领域。

不同于传统的贝叶斯理论，证据理论可以准确地区分缺乏信任和不信任两种概念。一方面，证据理论利用信任函数对具有不确定性的知识进行表示，克服了传统方法依赖于推理的先验知识或条件概率等诸多限制[13]；另一方面，证据理论能够合理地分配基本概率分布，将证据的剩余支持分配给整个辨识框架，从而可以更加有效地处理各类不确定性[14]，如模糊性、随机性等。因此，将证据理论的思想与模式分类方法相结合便可以有效提高分类器对具有不确定性数据的分析、表达以及处理能力。

根据分类方法的不同，证据理论在模式分类问题中的应用主要可分为两种：一是在作为单个分类器设计的核心思想时，将证据理论中对证据的处理及合成机制与分类方法相结合，即对“证据”进行表征处理后，通过一定的合成规则生成结果，以此来提高分类器的性能[15]；二是在作为多分类器集成的集成规则时，将基分类器的原始输出转化成软输出的形式，这些软输出的结果作为基本概率赋值，再用证据理论方法的组合规则将它们融合，从而通过融合多个不同分类器的结果来提高整体系统的分类准确率[16]基于此，为了全面总结、梳理证据理论在模式分类中现状及发展趋势，本文围绕单分类器设计和多分类器集成两大不同的应用场景，分别系统综述了证据理论在模式分类问题中的发展和应用过程，结合实际对各阶段不同方法的优缺点进行比较，并展望了证据理论在模式分类领域中的未来发展趋势。

1 模式分类概述1.1 模式分类的定义

模式分类作为机器学习领域一大重要组成部分，同时也是处理许多问题的重要工具[17-18]。早在二十个世纪七十年代，文献[19]中就给出了具体的定义：通过训练已知的数据集构造一个分类函数或者分类模型，再将新的数据集导入并映射到一个特定的类别之中，这样的一个过程就叫做模式分类。因此，根据上述定义，可将模式分类的过程分为数据输入、数据采集、特征提取与选择、模型选择、分类器训练和评价等多个部分，各部分具体流程如图1所示。

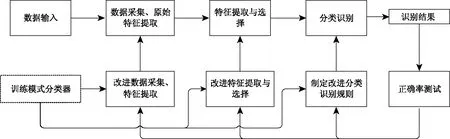
图1 模式分类具体过程

文献[20]认为在采集数据的过程中，数据量过小或过大都会对整个模型的性能指标造成影响，实验初期采用较少的小样本进行训练是可行的，但到后续无法保证已知数据具有足够的代表性供训练和测试阶段使用。同样当数据量过大时会消耗大量的实验成本，不利于研究的进行。综上所述，模式分类主要是预先通过训练样本训练得到一个分类模型，根据特征提取与选择最终将所采集数据的目标样本进行分类规则识别的一个过程。

1.2 模式分类基本方法

根据应用领域的不同，模式分类方法主要包括有支持向量机(Support Vector Machine，SVM)、k-近邻算法(K-nearest Neighbor，KNN)、反向传播神经网络(Back Propagation Neural Network，BPNN)、朴素贝叶斯(Naive Bayes，NB)、线性判别分析(Linear Discriminant Analysis，LDA)和证据理论(Dempster Shafer Theory，DST)等，各方法的优劣对比如表1所示。

表1 各模式分类方法优劣势对比

综上所述，现有的模式分类方法具有各自的优势并能够用来解决不同领域的相关问题，但由于方法自身存在的局限性，同一种方法很难做到适用于各种情况的分类问题。同时，当分类模式中的特征变量过多时，获取这些特征样本就会变得困难，使用上述传统的模式分类方法时会出现难以判别等情况[27]。证据理论在处理带有不确定性的输入信息时可对其进行有效描述，并实现证据的定量表达。这样做的好处是不仅在面对多分类和大规模的样本时能够保持较好的性能，还可以应对并处理非线性样本等复杂情况[8]。例如，在与朴素贝叶斯等方法相比，采用证据理论进行分类时，分类情况的好坏取决于可用数据，在构建好分类器之后，整体系统并不依赖于先验概率等其他参数，具有良好的稳定性和鲁棒性[28]。

2 证据理论概述

证据理论最早于1967年由Dempster提出，是一种经典的不确定性推理方法[29]。在证据理论中，通常用集合来表示命题。假设辨识框架Θ={H1,H2,…,HN}是由一组互不相容且构成完备集的命题所组成的集合[30]，即对于任意的i,j∈[1,N]且i≠j，恒有Hi∩Hj=∅。2Θ是Θ所有子集所构成的集合，表示辨识框架中一共包括有2N个子集。定义m为辨识框架上的基本概率质量函数，也称为mass函数，则有：

(1)

式中：Hi表示第i个命题；∅表示空集。除了基本概率质量函数(Basic probability assignment，BPA)之外，还有两个重要的核心函数：信任函数Bel和似然函数Pl，其具体定义为

Bel(A)=∑B∈Am(B)

(2)

Pl(A)=∑B∩A≠∅m(B)

(3)

式(2)中，Bel(A)表示命题A的全部子集的BPA之和，即命题A一定成立；式(3)中Pl(A)表示所有与命题A相交的子集的BPA之和，即不否认命题A的信任度。二者存在以下关系：

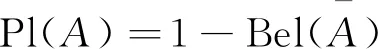
(4)

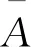
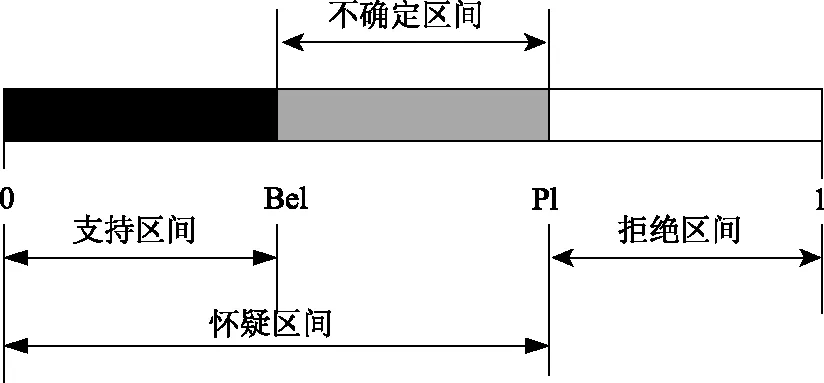
图2 不确定性表示

Dempster组合规则用于组合相互独立且完全可靠的证据，假设分别对应的BPA为m1和m2，对于任意的A∈Θ，则有：

(5)

然而，当证据之间存在冲突时，其往往会产生与常理认知相违背的结果，这种现象被称为“反直觉问题”[31]。另外，当证据数量超过一定限制时，Dempster组合规则的计算量会呈指数级提升，从而产生“组合爆炸”问题[32]。因此，在以上这些问题的基础上，相关学者分别从输入形式的表达以及组合规则的改进等方面对传统的D-S证据理论进行了深入的探讨和研究，后来逐渐形成了两种不同的分支形式即围绕信任函数[33]的证据理论和围绕置信分布[34]的证据理论，且二者都在解决不同领域的问题时发挥了重要的作用。

在信任函数方面，文献[33]首先提出了Pignistic概率转换和可传递信度模型，并将信任函数分配到辨识框架中的所有模糊子集上，实现了从mass质量函数到概率分布一系列的转化。文献[35]在Bayes的基础上提出了信任函数的Bayes近似计算公式，从公式的角度证明了信任函数之间信度的合成与Bayes近似计算是等价的，这大大减少了证据理论合成公式的计算量。文献[36]在组合证据的过程中首次采用了“等权法”的方式将证据进行统一平均赋值，这样做的好处是通过对权重赋值的方法提高了Dempster合成规则解决证据冲突问题的能力，进一步提升了证据合成的性能。在置信分布方面，文献[34]于1994年首次提出了证据推理算法(Evidential reasoning，ER)，而后，文献[37]进一步将ER算法推广到了区间推理的形式。2013年，文献[38]在考虑了证据权重的基础上首次引入了证据可靠度，形成了一般化的ER规则(ER-rule)。2017年，为了解决证据之间的相关度表示问题，文献[39]提出了一种新的最大似然证据推理框架，将状态空间模型和证据空间模型相结合，分别用于描述不同状态下的系统变化和数据映射。至此，证据理论的发展逐渐推向了一个新的高度，凭借其表示和处理不确定性问题的能力，其被广泛应用在安全性评估[40]、故障诊断与风险分析[41]、系统工程[42]等诸多领域。

综上所述，随着研究内容的不断推进和研究方法的持续创新，一方面，由于Dempster规则存在的合成证据冲突问题，在后续产生了多种证据合成的改进规则；另一方面，证据理论在发展过程中逐渐产生的针对于信任函数和置信分布的两种研究分支，各分支对于证据理论框架的研究侧重点也有所不同。因此，衡量和选取合适的证据合成规则，并将其应用于单分类器设计方法和多分类器集成方法之中尤为关键，而研究不同的合成规则所能造成的不同影响和性能差异也是目前需要分析和探讨的问题之一。

3 基于单分类器设计的方法研究现状

分类的核心思想就是把待分类数据通过某种机制映射到不同的类别当中，基于证据理论的单分类器设计方法是指将证据理论框架中关于证据不确定性的表示与合成思想与不同分类方法的具体过程相结合，从而使分类过程更具有一般化的特点[43]。根据证据理论在分类器设计过程中应用角度的不同，可将单分类器设计的方法分为基于信任函数的方法和基于置信分布的方法，接下来将从对应这两大分支不同的角度出发分别介绍其发展和应用研究。

3.1 基于信任函数的方法

基于信任函数分支的证据理论实质上是对于所输入证据信息表达方式的更新。将其应用至模式分类问题当中可以看作是在特征层面，把可以用来表征不同类别的特征样本看作是支持该类别的证据项，并为其分配信任函数，此时输入分类函数映射的不再是待分类样本自身，而是样本对应的证据项，证据项更新的同时也会得到不同的分类效果。

因此，众多学者开始从输入方式表达的角度将证据理论应用于单分类器的设计和改进，最早且较为经典的是1995年文献[44]率先提出的一种基于D-S证据理论的k-近邻分类规则算法。该方法把要分类样本的每个邻居都视为关于支持该模式类别类成员的某些假设的证据项，其中各类别的集合被定义为一个识别框架C={C1,C2,…,CM}，M表示该集合中的最大类别数，根据距离对不同证据项的不确定性进行量化，给出每个证据相应产生的基本概率赋值，利用组合规则将其融合，进而决策并判断出其所属类别。实验结果表明，在数据受到不同程度噪声扰动的情况下该方法仍能发挥出不错的分类性能，并且在此基础上还解决了原始k-近邻算法对不同的k值敏感的劣势，这得益于在引入了证据理论之后，每一个被分类的对象可以看作是对该模式类别成员不同的置信支持证据项，从而量化了复杂假设的不确定性关系。在Denoeux研究的基础上，1998年，文献[45]提出了基于证据理论k-近邻分类的进一步优化算法，其通过最小化误差函数的办法从数据中确定最优或近似于最优的参数值，并通过实验结果证明了该方法不仅保留了原始方法所有优点，还显著提升了优化后算法的整体分类性能。之后，在文献[45]的基础上，文献[46]又提出了一种新的针对于证据理论分类规则相似度参数计算的方法，该方法采用了统计概率学的思想，对每一模式分类的参考最近距离值进行估计，结果证明这种方法在处理小样本和非高斯分布情况下的数据时，不论是准确率还是运行效率都得到了较好的提升。在神经网络全连接理论的基础上，文献[47]于2000年设计并提出了一种基于证据理论的神经网络分类器，该方法同样将每个模式类的证据项用基本概率赋值的形式表示，合成过程则在特定架构的多层神经网络中实现，与之前的传统方法相比分类性能得到了明显提升。同年，文献[48]又提出了基于D-S证据理论的决策树规则分类器，解决了传统方法中树节点熵的度量问题，将类成员转换为信任函数的形式，并在EGG数据集上取得了更好的效果。但无论是基于证据理论的神经网络分类器还是决策树规则分类器，在处理数据不均衡的小样本问题时都很难发挥出其性能，因此，文献[49-50]针对基于训练样本数据不充分、不均衡的情况，提出了相应新的模式分类决策规则，进一步奠定了基于信任函数的证据理论在单分类器设计方面进行模式分类的理论基础。

文献[51]认为分类的不确定性主要是由于缺失数据的信息不足造成的，并将这一情况定义为“不完整模式分类”，为了解决这类问题，提出了一种基于原型的分类方法，将依托于原始训练样本获得的类原型用于估计样本缺失值，再利用信任函数框架对其进行表征，通过在人工和真实数据集上的测试结果表明这种组合规则可以有效地解决不完整模式的分类问题。文献[52]针对医学影像不确定性数据分类问题，将证据理论与深度神经网络进行结合，提出了一种基于证据神经网络的医学影像三支决策方法，在理论层次上对可能出现误判的影像进行证据函数的构造，实验验证结果表明，所提方法既解决了传统方法中受标注数据有限、数据表征模糊的问题，又能够有效地对具有不确定性的医学影像进行模式判别，对医学影像的处理与分析提供了理论支撑。文献[53]针对电影历史数据缺乏、可用变量少以及预测过程中的不确定性等特点，将XGBoost算法和D-S证据理论进行结合，首先利用XGBoost算法对已有样本数据进行有效划分，从而完成证据信任函数值的计算，然后将计算得到的信任函数值通过证据理论进行信息融合，最终得到一个票房归属区间，验证了该方法的有效性。

3.2 基于置信分布的方法

基于置信分布分支的证据理论是在经典证据理论的基础上，对证据组合过程中的置信分布表示进行新的定义与改进，常被用于解决不同的分类与决策问题。如前文中所提到的，文献[31]最早对于一条证据置信分布组成做出了如下定义[31]：

ei=(θn,pn,i),n=1,2,…,N;(Θ,pΘ,i)

(6)

式中：pn,i表示证据ei被定义为类别θn的概率置信度；i表示第i条证据；n表示第n个类别；对于每条证据对应不同的权重wi(i=1，2，…,L)，ER-rule则是引入了证据可靠度作为证据项的参数，后来的研究人员主要针对上述置信分布框架进行研究。

针对预测模型中各项参数难以主观精确设定的困难，文献[9]提出了一种基于证据推理的故障预报方法，通过对权重等模型参数进行优化学习，最终有效提升了模型的预测和模式分类的能力。在航天工程领域，文献[54]针对航天继电器中存在的大量强不确定性并发故障特征，提出了一种基于证据推理的航天继电器故障分类方法，该方法基于三阶Volterra滤波器对故障的特征变量进行分类，在求取合成规则权重的过程中首次用到了变异系数法，并于STS2104A电磁继电器系统上的大量实验验证表明了该方法的有效性。2016年，文献[55]基于证据推理规则提出了一种纯数据驱动的模式分类方法，该方法中充分考虑了主观和客观不确定性因素的存在，区分了权重和可靠度对于分类效果不同的影响，即前者表示属性或其证据对模式分类问题提供正确判断的能力，后者则反映证据在需要组合时与其他证据相比的相对可靠度。论文中该方法还详细阐述了从证据获取到权重、可靠度等参数的确定以及证据组合的过程，在UCI的五个公开数据集中都显示出了可以与其他经典方法相媲美的优异性能。

而后，文献[56]又在此前的基础上提出了一种改进型的基于证据推理规则的分类算法，针对之前方法中纯数据驱动，并不对证据属性和类别之间关系进行假设定义等特点，利用证据理论中的歧义测度，对属性样本和对应证据的不确定性进行量化处理，实验结果证明了改进后的方法更适用于解决定量数据和定性知识不确定的模式分类问题，且具有更高的分类精度。文献[57]对当前证据推理规则中参考值的设置进行改进，提出了一种基于证据推理规则的分布式参考值航天继电器性能分类模型，首先，为了有效嵌入专家知识并捕获性能信息，使用高斯分布来描述参考点，其次，通过对证据参数的计算和优化，构成一个完整的性能评价指标模型，最后在JRC-7M航空继电器进行了案例研究，以验证了所提出模型的有效性。针对客户投诉叙述中存在不准确或不一致信息的问题，文献[58]以基于证据推理规则的分类器作为核心开发了一种用于处理用户投诉的新型决策分类系统，通过对文本和数字特征的结合来生成证据，并以权重和可靠度的形式对这些特征与结果之间的关系进行量化，不仅可以生成分类结果还可以得到类别对应概率，与其他机器学习算法相比具有更强大的特征表示能力和分类处理性能。文献[59]基于贝叶斯网络和证据推理提出了一种新的模型聚合方法和多种数据源的船舶风险评估概率框架，其通过实际观测数据对风险参数之间的关系进行刻画，然后输入至贝叶斯网络和证据推理结合的分类模型之中，在考虑了其他综合特征的情况下建立了完整的风险评估模型，结果表明，该方法能够有效判断在多源数据场景下的风险类别，并为风险分析应用中使用多个数据源提供了经验证据。

3.3 基于单分类器设计方法小结

表2按时间顺序总结了上述基于两种不同分支方法的发展和应用研究内容，从这些工作中可以发现，将证据理论的原理及思想应用到单分类器的构造和设计中，可以有效提升单个分类器的分类性能。并且证据理论在处理不精确、不确定的信息时有着强大的组合与分析能力，这使得证据理论作为单分类器进行使用时有着更为宽广的应用范围。然而，由于证据分类器本身是从不确定性量化的角度出发的，从训练样本到证据函数的信息转换是一种近似于纯数据驱动的方法，因此如何根据不同的证据样本对证据函数进行合理构造有待进一步验证。值得关注的是，目前对证据理论分类方法的性能优化相关研究较少，因此，使用遗传算法之类的优化算法对分类模型的结构进行优化，从而使模型具有更好的结构和更轻量化的计算负担是一个较为开放的问题。

表2 基于单分类器设计的方法内容对比

4 基于多分类器集成的方法研究现状

多分类器集成在机器学习领域又被称为集成学习，其最早的研究是于二十世纪九十年代文献[60]在研究如何提高神经网络的性能时，通过调用相似网络之间的集成和交叉验证从而发现不同的神经网络在经过某种组合之后可以减少剩余的残差泛化误差，达到更好的训练和分类效果。在后来的研究中文献[61]提出了一种基于Boosting算法的支持向量机基学习器集成方法，研究结果证明Boosting的集成方法在保证分类精度提高的同时还可以有效防止过拟合等问题。

证据理论中包含有信任函数和置信分布两大基本概念，在处理决策层不确定性信息的表示和融合时具有强大的推理能力。因此，将证据理论引入到多分类器集成当中可以获得更加优异的分类性能，具体的理论框架如图3所示。

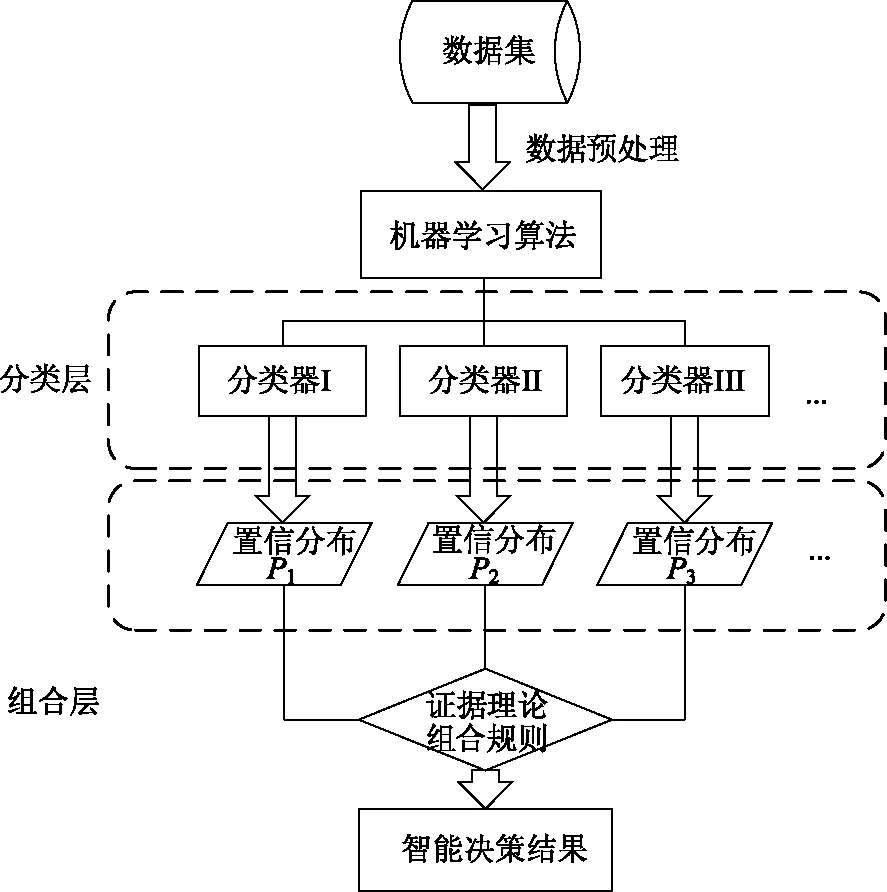
图3 基于证据理论的多分类器集成过程

在该框架形成的基础上，众多学者并没有从严格意义上的信任函数和置信分布分支进行改进，更多地则是针对多分类器集成系统的不同层面纷纷开展研究。因此，证据理论在多分类器集成方面的应用可分为基于分类层改进的方法和基于组合层改进的方法。

4.1 基于分类层改进的方法

如图3所示，在基于证据理论的多分类器集成系统中，针对于各个成员分类器的选择与分类层次的方法称为分类层。在模式分类问题中，现实生活中的数据存在着各种各样的不确定性，使用不同的样本数据或不同种分类方法来训练学习得到的不同的分类器相互之间具有关联性和互补性，如何合理利用各成员分类器之间的差异性和相关性对提升整个系统的分类性能往往具有至关重要的作用[62]。因此，在此基础上，部分学者陆续提出了众多关于选择性度量和改进多分类器之间差异性关系的证据理论模式分类集成方法。

文献[63]基于证据距离的度量提出了一种新的分类器差异性度量方法，并首次将概率分配分为了贝叶斯基本概率分配和非贝叶斯基本概率分配，通过在不同测试样本上提取关键特征向量，利用KNN算法得到其概率质量作为单类焦元mi(Cj)，其中i表示第i个特征子空间，j表示第j个基分类器，这样可以计算每一类别中样本的中心距离从而获得新的概率赋值。文献[64]针对多分类器系统构造过程中可能出现的“差异性淹没”问题，提出了一种基于几何关系的多分类器差异性度量方法，该方法可以对不同分类器的分类结果之间的差异性按照规则进行有效刻画，最终以各个几何中心之间的离散程度作为度量方法，对比实验结果证明可以有效提升分类结果的准确率。文献[65]针对基于证据理论的多分类器系统设计，提出了一种新的使用最短特征线段分类器的多分类器系统，该方法利用最短特征线段分类算法的工作机理实现了成员分类器之间模糊隶属度的建模与度量级融合，从而使多分类器系统有效实现了多分类器之间隶属度关系到mass函数的转化。文献[66]通过对样本不断地有放回抽样形成多个版本，提出了一种基于生成多个训练样本来获得不同成员分类器的选择性集成并行融合算法，该算法创新性地采用MapReduce并行化处理有效解决了传统分类器差异性选择过程中可靠性和扩展性不足的特点，最终用证据理论将得到的并行多分类器结果融合，结果表明所提出算法可以显著提高分类结果的准确率。文献[67]在研究基于证据理论的多分类相关向量机(Multi-class Relevance Vector Machine，M-RVM)多分类器集成过程中，采用四个不同类型的M-RVM基分类器，同时引入兰氏距离函数和光谱角余弦函数对分类器进行差异性度量，优化后得到的分类器组合被证明具有更好的性能。

4.2 基于组合层改进的方法

如图3所示，在基于证据理论的多分类器集成系统中，将证据理论的组合规则用于融合各分类器的结果以获得更高的准确率，该方法层被称为组合层。组合规则往往对应着融合了系统各分类模型之间输出性能的优势，找到一种合理的组合规则对提升整体系统的分类效果具有至关重要的作用。

基于此，文献[68]提出了一种基于证据理论的多分类器组合方法用于手写识别等领域的应用，该方法根据分类器所能提供的可用信息不同，讨论了几种分类器的组合方式，通过正确识别率，替换率和拒绝率来得到基本概率赋值，并输出成员分类器分类结果的输出向量φi(d)，其中i表示第i个成员分类器，最终决策结果由BPA之间的组合结果以及对某一类别的最大支持程度得到，在美国邮政编码数据库上验证得到了较高的识别率，与其他方法相比，识别性能也得到明显提升。文献[69]提出了一种新的基于证据推理的最优加权分类器组合方法来提高分类精度，通过最小化Dempster规则得到的组合结果与训练数据空间中的目标输出之间的距离来获得分类器的最优权重因子，以充分利用分类器的互补性，并在UCI公开数据集中证明了其方法的有效性。文献[16]为了实现对分类数据不确定性的有效表示，提出了“混合类”的概念，将训练数据中的含混数据做了新的标注，并使用证据神经网络对分类输出进行建模，采取不同的证据组合函数组合多个分类器的结果，实验证明获得了较好的效果。文献[70]为了解决多分类器集成系统对基分类器的分类性能要求较高等问题，提出了一种基于Shapelets的多变量证据加权集成分类方法，在单变量时间序列上学习得到基分类器Shapelets及其权重的赋值，最终在标准数据集上获得了较好的分类结果。文献[71]利用基于证据理论的多分类器融合框架将机器学习中的朴素贝叶斯与支持向量机的分类结果进行融合，对中文微博进行观点句义判别并在NLP&CC 2012提供的数据集上验证得到了更好的召回率和F值；文献[72]在铁路货运列车能耗统计判别的领域中提出了一种基于证据推理理论的支持向量机集成学习方法，将通过训练集样本得到的各个不同支持向量机分类器作为基学习器，并将基学习器的AUC值作为量化权重的判断依据，利用证据推理算法组合各基学习器的分类结果，最大置信度的类别结果即作为系统的决策判别结果；文献[73]在研究室内多径传播及非平稳信道环境时，提出了一种基于证据理论的群指纹融合高精度室内定位算法，通过各种手段采集到各种样本特征，并用神经网络针对每种特征分别训练出不同的神经网络分类器，利用证据理论对分类器生成的分类结果融合得出最终目标定位，仿真结果表明所提出算法具有良好的有效性和可行性；文献[74]从结构参数、证据距离以及组合规则的角度对传统的证据k-近邻分类器进行优化，并结合了非线性偏最小二乘和支持向量机分类器的分类结果建立了证据理论多分类器融合系统，实验结果表明，该模型可以大大提升系统的类别监测精度，从而符合更加复杂的生产情况。

4.3 基于多分类器集成方法小结

表3总结了上述基于不同层面的改进方法，从中可以看出，证据理论应用在多分类器系统融合的决策层可以解决单一分类器无法实现有效分类等问题。使用多个不同的分类器进行分类，并将结果用证据理论进行融合可以明显提升分类性能，同时更好地利用了分类器之间的互补性和相关性，从而使得多分类器系统可以更好地解决复杂的模式分类问题。然而，现有工作往往更多地注重于在多分类器系统决策层做出改进，容易忽略集成系统中各个成员分类器之间的差异性，因此在选择分类器时如何将成员分类器之间的性能表现进行差异性度量需要进一步地探索。与此同时，各分类器之间权重和可靠度的确定也与特征指标的主观评估和分类效果的可靠性息息相关，如何对权重、可靠度进行确定和优化也同样值得关注。

表3 基于多分类器集成的方法内容对比

续表3

5 结 语

本文从模式分类问题的角度出发，首先论述了模式分类的基本概念、流程和现有的一些分类方法，再对证据理论的发展与应用做了概括，将证据理论在模式分类问题中的应用分为单分类器设计和多分类器集成两大类，并分别针对于这两个应用场景，系统性地梳理了国内外在该领域较为经典的相关文献和主要研究现状。

通过综述研究可以发现，证据理论无论是在单分类器设计，还是在多分类器集成方面都可以凭借其强大的不确定性信息处理能力和对证据函数优秀的组合能力应对各种复杂的模式分类场景，但其本质上仍属于一种严格的联合概率推理过程，因此在具体应用中还存在有一些不足之处：

1)证据之间的独立性证明和非独立性联合。在多分类器集成的过程中，各分类器所生成的不同结果，往往看作是彼此独立且互斥的，因为它们一般都产生自于不同的分类函数或特征向量当中，但当证据理论充当单分类器设计的核心理论时，如何证明两条或多条需要组合的证据是独立的，这有待进一步研究。尽管目前在研究界人们更倾向于将证据之间的组合定义为是加性的，但能够给出更为合理的证明才能使得其在具体应用过程中更具有说服力。此外，现有的方法大多都是考虑了独立证据之间的组合，在未来的研究与发展过程中，如何将非独立性证据通过一种新的组合规则联系起来，从而用于解决更多的模式分类问题，其具有深远的研究意义；

2)证据函数的生成与差异性度量。将Dempster组合规则用于多分类器的集成与融合时，关键的一个问题则是如何根据各分类器的不同特性生成证据函数。证据函数是证据理论的基础，机器学习通过训练和学习得到的结果可以通过各种手段转换为置信分布的形式表示为证据，而对于不同证据项之间存在的差异性需要一个更为合理科学的度量方法。在集成系统当中，各基分类器往往具有不同的分类特性，这种差异性的度量被认为是提高系统整体分类性能的一种有效手段，因此，针对基分类器之间存在的差异性问题，设计更加有效的差异性度量损失函数也是未来亟待探索的关键性问题；

3)证据权重与可靠度的计算和优化。随着现代研究的不断深入，证据的权重与可靠度被认为是重要的推理参数，因此，这些参数的表示与计算逐渐成为证据理论在置信分布结构下的一个重点问题。目前，大多数研究在权重与可靠度等参数的表示计算和优化方面，只结合了当前工程应用背景下的情况，不具有更加宽泛的应用范围，在未来的工作中，如何提出一种更具有普适性和鲁棒性的参数确定及优化方法同样是一个值得思考的问题。同时，不同的分类方法采用不同的分类机制和原理，如何通过对参数的优化来提升证据理论模式分类方法的泛化能力也是一个长远的话题。