矩阵线性互补问题误差界的新估计式

赵 英 霞 王 峰

（贵州民族大学数据科学与信息工程学院，贵州 贵阳 550025）

1 引言

M-矩阵是应用广泛的一类重要矩阵，与许多学科领域有着密切的关联，经济学、生物学及社会科学中有大量问题和M-矩阵有着必不可少的联系. 且严格对角占优M-矩阵A的逆矩阵的‖A-1‖∞上界估计在数值代数中有着重要的应用，在代数方程组的收敛性条件及条件数需计算‖A-1‖∞，可当M-矩阵的阶较大时，其逆矩阵求解复杂，因此对‖A-1‖∞上界进行估计是十分重要的.近年来，许多学者对M-矩阵的逆矩阵的无穷大范数上界进行了估计，得到了很多好的结果［1-12］.另外，特殊结构矩阵线性互补问题是一类在工程学、经济学、控制论等领域具有重要应用价值的优化问题［13-16］.对于给定的n阶矩阵A=(aij)∈Rn×n，n维实向量q∈Rn，用LCP(A,q)来表示矩阵A的线性互补问题，寻找x∈Rn，使其满足

2 预备知识

为叙述方便，给出一些记号.设A=(aij)∈Rn×n，aii≠0，m≤i,j,k≤n，ε＞0，且

定义1［2］设A=(aij)∈Rn×n，如果对任意的j,i∈N,i≠j，都有aij≤0，则称A为Z-矩阵，记A∈Zn.设A∈Zn，则A可表示为A=sI-B，其中B≥0.当s≥ρ(B)时，称A为M-矩阵；当s＞ρ(B)时，称A为非奇异M-矩阵.

定义2［3］设A=(aij)∈Rn×n，如果满足下面条件

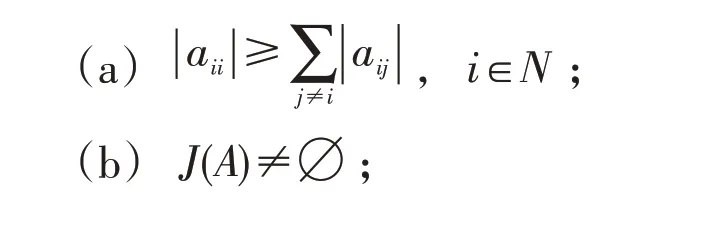
（c）对于任意i∈N，i∉J(A)，存在i1，i2，…，ik，使得aii1ai1i2,...,aik-1ik≠0，ik∈J(A).则称A为弱链对角占优矩阵.

定义3［3］设A=(aij)∈Rn×n，若J(A)=N，则称A为严格对角占优矩阵.

定义4［25］设A=(aij)∈Rn×n，若

则称A为B-矩阵.

3 主要结果

首先给出一些引理.

故定理4改进了文献［8］中的定理3.4，进而优于文献［2］中的定理3.3和文献［7］的定理3.2.

2009年García-Esnaola等［13］给出如下结果：设A=(aij)∈Rn×n为B-矩阵，将A表示为A=B++C的形式，其中

综合上述知（14）式成立.

下面对估计式（11）式与（14）式进行比较.

定理7 设A=(aij)∈Rn×n是B-矩阵，令A=B++C且B+=(bij)形如式（9），则

综上可得（14）式优于（11）式.

4 数值算例

下面用数值例子说明新估计式比已有的一些结果更加精确.

例1 设

显然A是严格对角占优的M-矩阵.应用文献［2］中的定理3.3，文献［7］中的定理3.4及文献［8］中的定理3.2，分别得

表1 的上界

表1 的上界

n（11）式（12）式（13）式（14）式10 104.9084 90.8111 83.6275 78.5563 20 415.8320 361.6667 332.8539 306.0755 50 2.8859e+3 2.1573e+3 1.9584e+3 1.1876e+3 100 9.5301e+3 7.1042e+3 5.3078e+3 3.2824e+3

5 结语

本文给出了严格对角占优M-矩阵及逆矩阵之间的元素关系式，通过迭代法获得了严格对角占优M-矩阵的逆矩阵的无穷大范数的新上界.同时，利用新上界与两个重要不等式放缩技巧得出B-矩阵线性互补问题误差界的新估计式，理论证明及数值算例表明了新估计式的有效性.