开式自然循环系统不稳定性实验研究

孙运达，元一单，李 晗，尹 令，龚圣捷,*

开式自然循环系统不稳定性实验研究

孙运达1，元一单2，李 晗1，尹 令1，龚圣捷1,*

（1. 上海交通大学核科学与工程学院，上海 200240；2. 中国核电工程有限公司核电安全研究中心，北京 100840）

核电站非能动安全系统依靠自然循环将热量导出，然而系统中的驱动压头、流动阻力、流量等相互影响，容易引发流动不稳定性，导致流动沸腾临界热流密度大幅降低，带来安全问题。因此，流动稳定性是自然循环热力系统的重要研究对象。本文以开式竖直加热圆管为实验本体，通过实验和物理建模的方法，研究了自然循环条件下管内间歇沸腾现象和流动不稳定特性。研究结果表明：随着热流密度的升高，系统将经历初始状态、低频脉动、高频脉动和稳定的自然循环四个阶段。基于实验数据，建立了不稳定边界的预测模型，预测值和实验值符合良好，误差在±10%内。

开式系统；间歇沸腾；自然循环；不稳定性边界

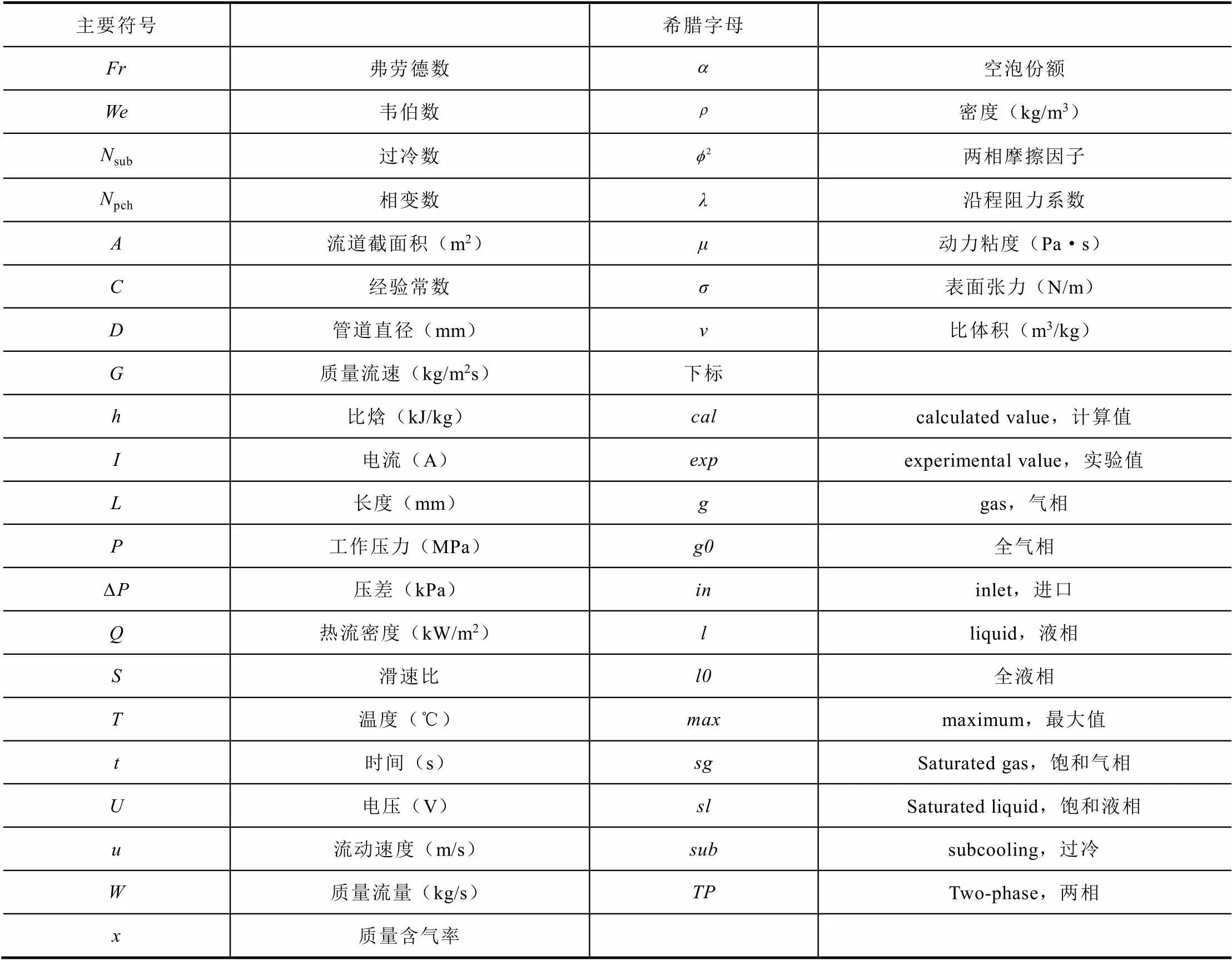
符号表

压力容器外堆芯捕集器技术（EVR）[1]是缓解严重事故后果的重要手段之一。现有的堆芯捕集器的冷却时间较长，以VVER冷却过程[2]为例，熔融物冷却固化需要10个月。为了提高冷却效率，加快事故缓解进程，研究者提出了一种内部布置有若干冷却管的双层坩埚式滞留装置的概念方案设计。

自然循环系统在低压下常有流动不稳定现象发生。Stenning等[3]基于不同脉动特征和发生区域，将实验现象分为压降不稳定性、密度波不稳定性和热力不稳定性，这种分类方法后来被广泛接受和应用。随着研究的不断深入，流动不稳定性产生原因和主要影响因素被国内外学者广泛关注。Omakl等[4]指出密度波型脉动的脉动幅值和脉动周期随着质量流速的减小而逐渐减小。Khazaee[5]指出随热流密度和长径比的增长，间歇沸腾周期逐渐降低。Mao等[6]基于VOF方法对间歇沸腾现象进行数值研究。结果表明，沸腾停滞时间占整个间歇周期的90%以上，在加热段直径不变的情况下，随着长径比的增大，间歇沸腾的强度持续增加，朱力[7]也得出了类似的结论。陈金波[8]认为加热段直径超过界限值后，间歇沸腾现象不会发生。

目前，针对开式系统间歇流动不稳定性的研究侧重于参数效应分析，对不稳定性边界的预测研究还比较少。本文以内置冷却管作为研究对象，在自然循环条件下，开展间歇沸腾实验研究。通过实验现象、间歇参数和PDF曲线分布特征，将本实验分为初始阶段、低频脉动阶段、高频脉动阶段和稳定阶段，并给出了流动不稳定性边界。最后通过自然循环系统的控制方程，给出流动不稳定性的预测模型。

1　实验研究方法

实验回路系统和实验本体测点布置如图1所示，实验选用仪表参数如表1所示。根据Moffat提出的误差传递公式[9]，得到各参数的最大相对误差如表2所示。流体在不锈钢水箱中预热达到预定工况后，启动直流电源对加热段进行加热，依靠流体密度差所产生的驱动压头来实现流动循环。

实验本体分为加热段和透明观察段两部分，分别由430不锈钢管和PC管构成，加热段管壁外侧镀有厚度均匀的发热膜。实验段有效加热长度为200 mm，内径为28 mm。

加热段的进口温度由热电偶（1）测量得到，加热段外壁面的温度分别由4支热电偶测量，测点距加热段入口分别为25 mm（2）、100 mm（3）、150 mm（4）和190 mm（5）处。加热段出口处布置有压力脉动传感器（），加热段和上升段两端布置有压差变送器（∆1和∆2），采集频率均为10 Hz。实验参数范围：入口过冷度为0～70 K，热流密度为0～1200 kW/m2。

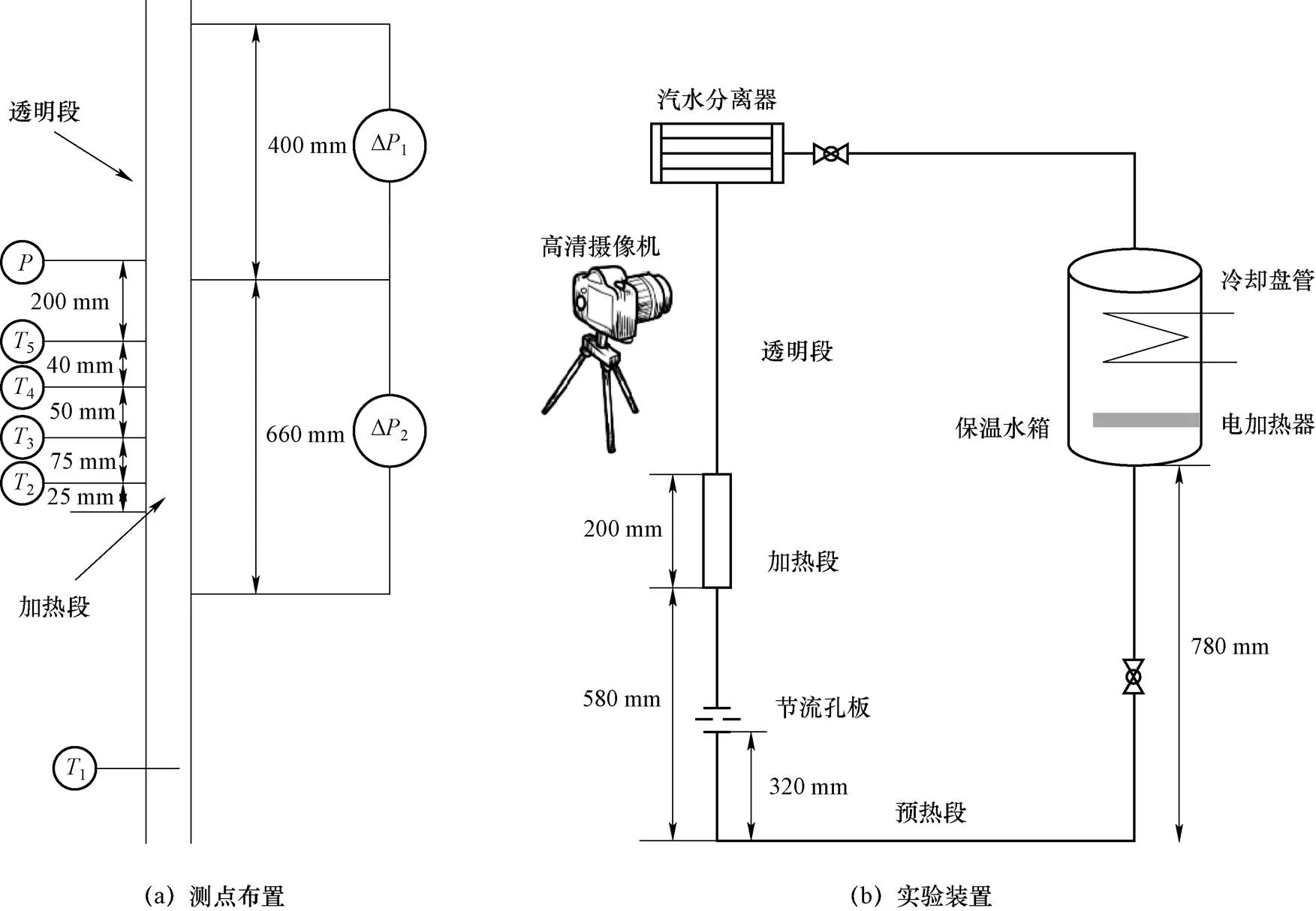
图1　实验回路系统

表1　实验仪表及参数

续表

表2　各物理量相对误差

2　实验结果

2.1　间歇沸腾现象及特征

图2给出了=602 kW/m2，Δsub=35 K工况下，一个间歇周期内（1～4）加热段压差和出口压力的时域图。在管内流体接近饱和温度前（1～2），加热通道流型为泡状流，出口处压力较低。当输入热量达到一定程度时（2～3），加热通道内流体达到饱和温度，小气泡逐渐聚合并形成较大的气泡，流体剧烈沸腾，气相夹带着液相高速喷涌进入上升段，流型转化为弹状流。在间歇沸腾阶段，重位压降起主导作用，由于两相流体从加热段涌入透明段，此时加热段压降下降至周期内最小值，出口处压力上升到最大值。随后上升段内流体冷却回流（3～4），出口处压力也随之下降，系统重新回到沸腾停滞阶段。

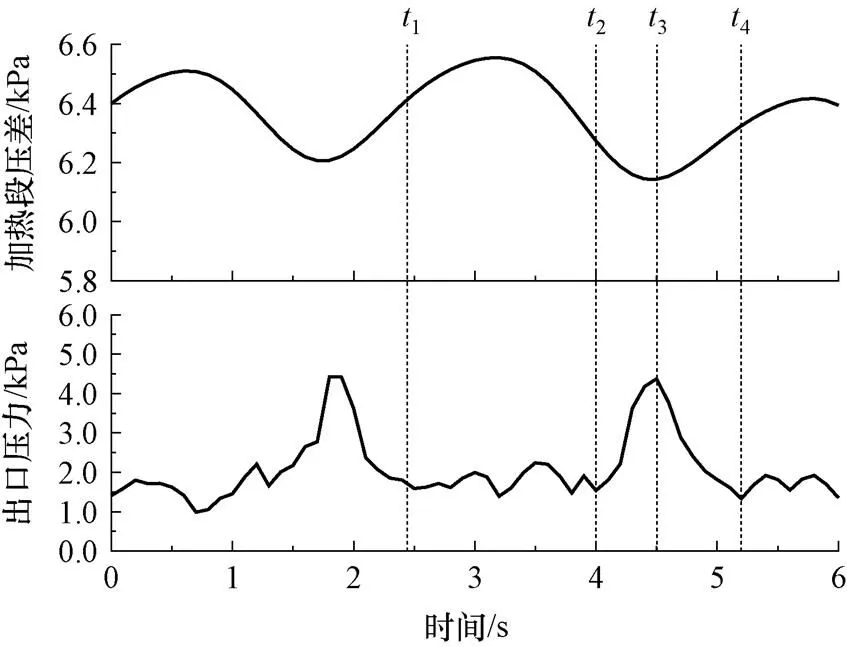
图2 间歇式不稳定性的时域特征

图3为不同工况下的加热段压差值的特征时域图。图3（a）给出了在=54 kW/m2，Δsub= 67 K时，加热段压差的时域特征。此时系统处于初始阶段，随着热流密度增大，壁面温度升高。加热段内较低的流速使得近壁面处流体和主流间的温差较大，进而使得流动过程呈现出较强的对流特征。随着热流密度进一步增加，开始出现沸腾，并产生间歇式流动不稳定，系统进入低频脉动阶段。

对压差时域曲线结合视频可视化文件进行分析。图3（b）给出了在=305 kW/m2，Δsub= 67 K时，加热段压差的时域特征，属于低频间歇沸腾，间歇周期较长。结合视频文件可得，图 3（a）中A、C、D处压差处于峰值时，间歇沸腾的液位处于最低位置，AC、CD分别是一个间歇沸腾周期，周期时间分别为7.6 s和8.8 s。而根据视频观察，处于压力峰值处的B点并没有处于间歇沸腾液位最低位置，AB、BC并不是低频间歇周期。选取5组典型的低频脉动工况，每组工况的采集时间30 s，采集频率10 Hz，共1 500个数据点。通过数据分析，发现在低频脉动阶段，间歇周期变化范围为：4.3～9.1 s。

当热流密度进一步增加，可以观察到明显的沸腾停滞现象，系统进入高频脉动阶段。图3（c）为=602 kW/m2，Δsub=35 K时，加热段压差随时间的变化情况，间歇周期较为规整，压差信号有清晰峰值与间歇周期相对应，如EF和FG。随着热流密度增加，间歇沸腾周期会逐渐减小。选取5组典型的高频脉动工况，每组工况的采集时间30 s，采集频率10 Hz，共1 500个数据点。通过数据分析，发现在高频脉动阶段，间歇周期较为稳定，周期变化范围为：2～2.9 s。

随着入口过冷度降低、热流密度升高，加热段压差的周期性变化消失，回路形成稳定的自然循环，如图3（d）所示。

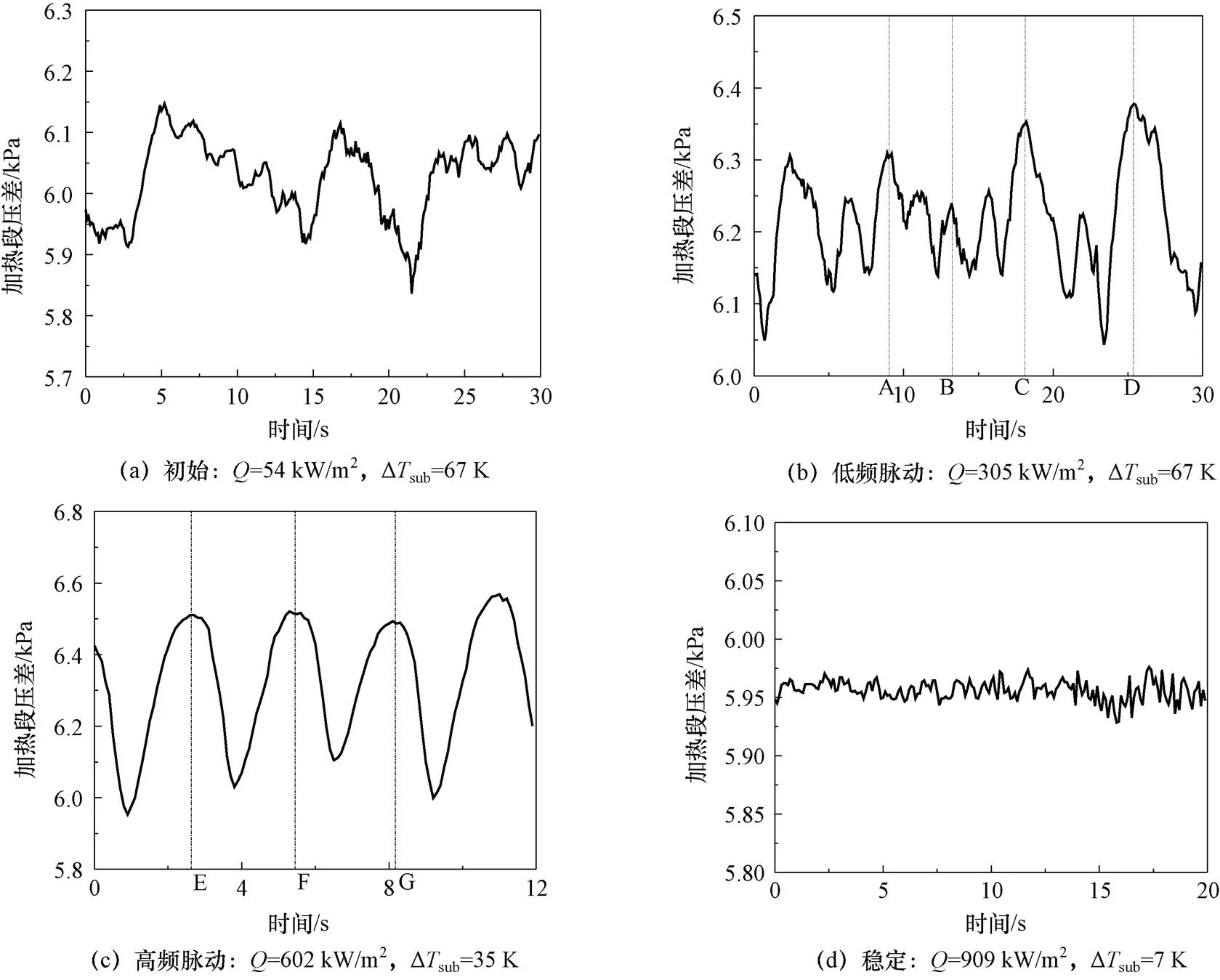
图3　系统不同阶段压降特征

为了进一步分析流动不稳定特性，采用概率密度函数（PDF）对加热段无量纲压差信号∆*（式1）进行分析。

式中：

∆——加热段压差的瞬时值，kPa；

不同工况下，∆*的概率密度分布如图4所示。低频脉动阶段，PDF曲线呈双峰不对称分布，曲线范围集中在±0.4内。高频脉动阶段，PDF曲线范围增大，峰值位置下降，概率密度函数曲线呈双峰分布，说明压差波动幅度增大，实验系统趋向不稳定。稳定的自然循环阶段，概率密度函数曲线呈狭窄的单尖峰分布，压差波动范围大幅下降，此时压差值保持稳定，系统由流动不稳定阶段过渡到稳定阶段。

图4　不同工况下∆P*概率密度分布特征

2.2　间歇沸腾影响因素分析

对于自然循环回路，加热通道的热流密度对间歇不稳定流动行为有重要影响。图5给出了过冷度为39 K，热流密度=350～600 kW/m2条件下，间歇沸腾周期变化情况。可以看出，随着系统热流密度的增大，间歇周期由3.23 s下降至2.72 s。图6给出了过冷度为39 K，热流密度=350～600 kW/m2条件下，无量纲压差在单个工况下最大值的变化情况。随着系统热流密度的增大，无量纲压差最大值由0.39上升至0.78。当过冷度较大时，随着热流密度的增大，压差波动范围增加，系统趋向于不稳定。

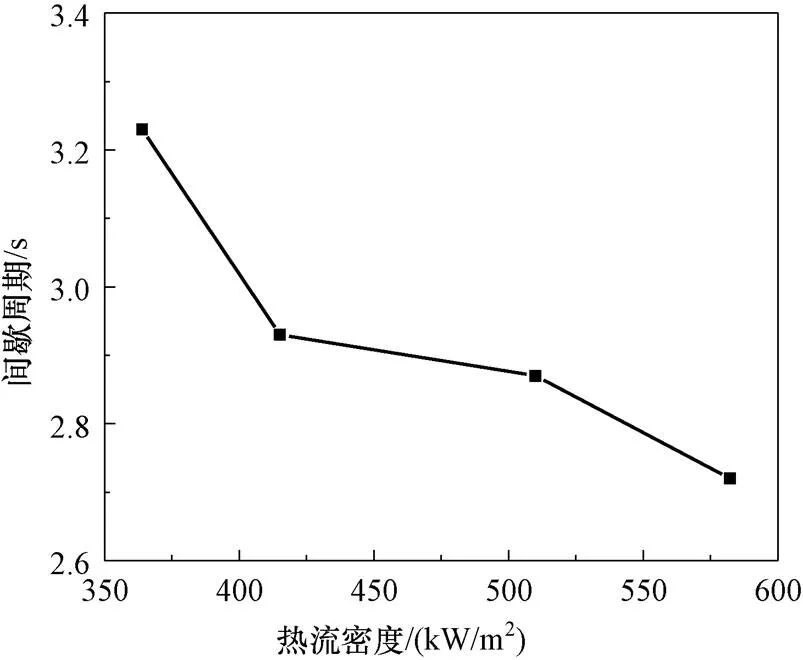
图5 热流密度对间歇周期影响

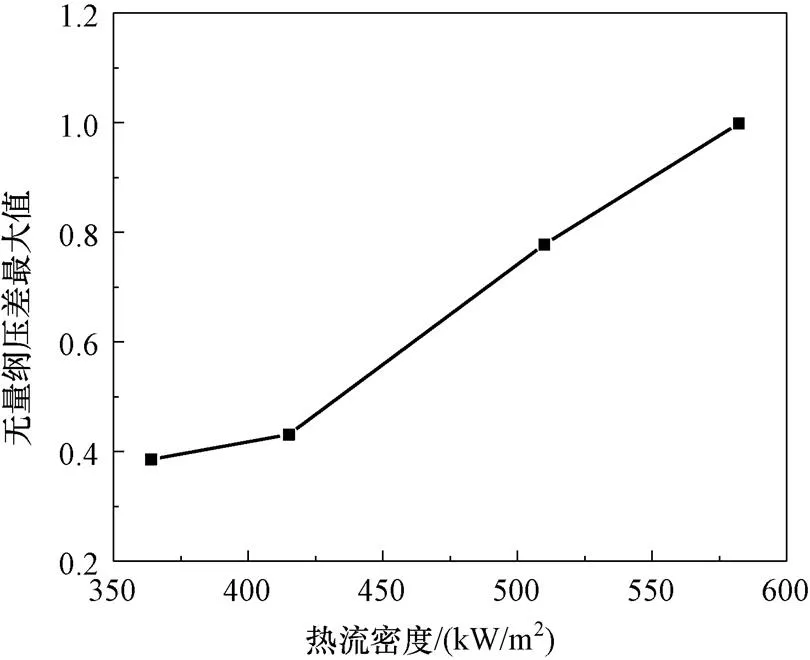
图6 热流密度对无量纲压差最大值影响

随着系统的过冷度降低，热流密度对不稳定流动现象的影响将不相同。图7给出了过冷度为7 K，热流密度=400～1000 kW/m2条件下，无量纲压差在单个工况下最大值的变化情况。随着系统热流密度的增大，无量纲压差最大值由0.26下降至0.13。这表明，在过冷度较低的工况，随着热流密度的增大，加热通道的压差信号波动幅度降低，系统趋向于稳定。

图7 低过冷度工况热流密度对间歇沸腾的影响

3　分析与讨论

3.1　自然循环流量计算

两相流动的总压降由摩擦压降∆f、加速压降∆a和重位压降∆el构成：

本文通过实验测量的上升段两相压降，计算获得自然循环流量。在动量方程中，重位压力梯度和加速压力梯度分别表示为：

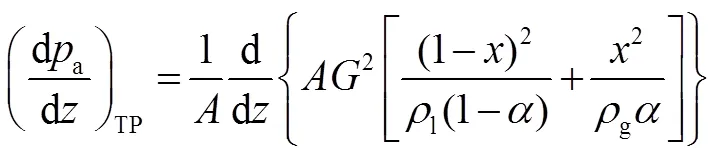
式中：

——流道截面积，m2；

——质量流速，kg/（m2·s）；

——质量含气率；

下标g、l——气相和液相。

两流体模型具有较高的模拟精度，本文采用滑移模型[10]，滑速比公式如下：

式中：

l0——全液相流动速度，m/s；

——工作压力，MPa。

若流道内流体总的质量流量为，气相流体的质量流量为g，液相流体的质量流量为l，即：

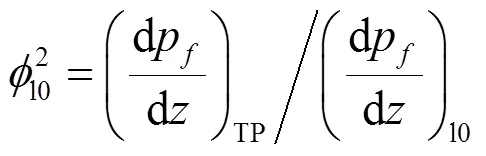
本文采用适用范围广的Friedel公式[11]计算。

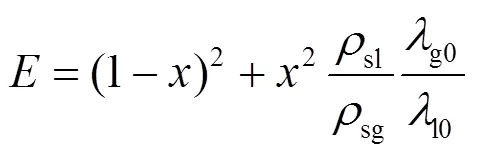
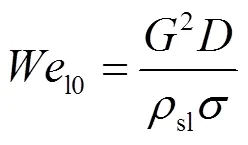
式中：

——沿程阻力系数；

——动力粘度，Pa·s；

——管道直径，mm；

——表面张力，N/m；

下标sl和sg——饱和液相和饱和气相。

l0和g0采用如下方法进行计算：

若Re≤1 055

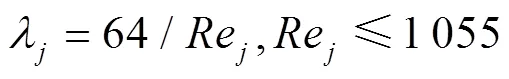
若Re＞1 055

下标可取“l0”或“g0”，分别代表全液相或全气相。

采用滑移模型[10]和Friedel模型[11]，对实验件透明段内绝热两相流进行分析计算，计算流程如图8所示，基于测量的压差，获得自然循环流量。

图8　计算程序流程图

图9为在入口过冷度为9 K，流动处于稳定工况下，自然循环流量随热流密度的变化曲线。随着热流密度的升高，自然循环流量呈逐步上升的趋势。

图9 自然循环流量随热流密度变化

3.2　不稳定边界划分

王强等[12]基于热流密度和入口过冷度来划分不稳定性边界。本文通过实验观察和数据分析将流动工况分为四个阶段。初始阶段：透明段观察到间歇现象发生前，压差无规律波动。低频脉动阶段：PDF曲线呈双峰状不对称分布，峰值在2.5～3.5，没有稳定的间歇周期。高频脉动阶段：PDF曲线呈双峰分布，峰值下降，低于2.5，间歇周期降低且趋向稳定。稳定阶段：压差和压力信号的周期性变化消失，PDF曲线呈狭窄单峰分布，此时峰值大于3.5。以此标准获得的流动不稳定区域如图10所示。

图10　不稳定性边界划分

针对自然循环流动，流动状态与两相密度、进口过冷度、质量流量和热流密度密切相关，以过冷数sub和相变数pch为横坐标和纵坐标，给出流动不稳定性区域如图11所示。其中，无量纲的过冷数和相变数表达式如下[13]：

（17）

式中：

——比焓，kJ/kg；

——比体积，m3/kg。

从图中可以看出，对于过渡工况，过冷数sub和相变数pch近似线性分布。随着热流密度升高，系统稳定性增加，工况点向右移动。

采用文献[14,15]给出的方法对实验系统的守恒方程进行循环积分，并将两相参数无量纲化，可以得到适用于开式自然循环系统的间歇式流动不稳定性临界状态方程式：

式中：

w——流动不稳定性消失点的热流密度，kW/m2；

lg——汽化潜热，kJ/kg；

0、1和2——经验常数，根据实验数据拟合获得。

利用式（18）对本实验过渡工况的实验数据进行拟合，可得：

利图12给出了流动不稳定性边界热流密度计算值和实验值的比较分析。可以看出，实验值和预测值误差小于±10%，该模型可以很好的预测自然循环系统流动不稳定边界的热流密度。

4　结论

本文通过实验和理论分析的方法，研究了竖直管自然循环下的流动不稳定现象及其影响因素，结论如下：

（1）竖直管自然循环流动时，随着热流密度的升高，分别观察到了初始阶段、低频间歇沸腾、高频间歇沸腾、稳定自然对流四个阶段，可基于概率密度函数区分：低频脉动阶段，PDF曲线呈双峰状不对称分布，峰值在2.5～3.5；高频脉动阶段，PDF曲线呈双峰状且近似对称分布，峰值低于2.5；稳定自然循环阶段，PDF曲线峰值大幅提升，概率密度函数曲线呈狭窄的单峰分布。

（2）过冷度和热流密度是间歇沸腾的重要影响因素。过冷度较高的工况，随着热流密度的升高，间歇周期减小，压差波动范围增大。过冷度较低的工况，随着热流密度的升高，压差波动范围降低，系统趋向稳定。

（3）采用过冷数sub、相变数pch和系统守恒方程无量纲化的方法可以较好的预测流动不稳定性边界，计算结果和实验值符合良好，误差在±10%内。

［1］ Fischer M．The severe accident mitigation concept and the design measures for core melt retention of the European Pressurized Reactor（EPR）［J］．Nuclear Engineering and Design，2004，230（1/3）：169-180．

［2］ 郑滨．田湾核电站堆芯捕集器内熔融物长期冷却过程的估算［C］．中国核学会全国反应堆热工流体会议，中国核学会，2003．

［3］ Stenning A．，Veziroglu T．Flow oscillation modes in forced convection boiling［C］．Proceedings of the 1965 Heat transfer and Fluid Mechanics Institute，Standford Univ. Press（1965），1965：301-316．

［4］ Omakl A，Karsl S，Yilmaz M．Experimental investigation of two phase flow instabilities in a horizontal in-tube boiling system［J］．Energy Conversion and Management，2002，43（2）：249-268．

［5］ Khazaee I，Hosseini R，Noie S H．Experimental investigation of effective parameters and correlation of geyser boiling in a two-phase closed thermosyphon［J］．Applied Thermal Engineering，2010，30（5）：406-412．

［6］ Mao H W，Li Y Z，Wang L，et al．Investigation of appearance and intensity of geyser phenomenon in a vertical cryogenic pipe［J］．International Journal of Heat and Mass Transfer，2020，150：1-13．

［7］ 朱力，陈金波，宫海光，等．低压加热通道内间歇式流动特性分析［J］．核动力工程，2015，36（1）：23-27．

［8］ 陈金波．低压竖直加热通道内间歇式两相流动不稳定性研究［D］．上海：上海交通大学，2015．

［9］ Moffat R J．Using Uncertainty Analysis in the Planning of an Experiment［J］．Journal of Fluids Engineering，1985，107（2）：173-178．

［10］贾志海，蔡小舒．基于滑速比的气水两相流气相流量计算方法研究［J］．工程热物理学报，2008，29（2）：259-262．

［11］唐国力，吴玉新，顾君苹，等．垂直上升光管中气液两相摩擦因子分析［J］．清华大学学报（自然科学版），2020，60（6）：55-61．

［12］王强，高璞珍，王忠乙，等．低压高过冷度下自然循环流动不稳定性实验研究［J］．原子能科学技术，2018，52（05）：822-828．

［13］谭思超，庞凤阁，高璞珍．低压两相自然循环流动不稳定实验研究［J］．哈尔滨工程大学学报，2006，27（02）：218-222．

［14］吕书平．窄矩形通道中压降及自然循环流动不稳定特性研究［D］．重庆：重庆大学，2014．

［15］杨瑞昌，王彦武，王飞，等．自然循环过冷沸腾流动不稳定性的实验研究［J］．核动力工程，2005，26（4）：317-322．

Experimental Study on the Instability of the Open Natural Circulation System

SUN Yunda1，YUAN Yidan2，LI Han1，WANG Junjie1，GONG Shengjie1,*

（1. School of Nuclear Science and Engineering，Shanghai Jiao Tong University，Shanghai 200240，China；2. Nuclear Power Safety Research Center，China Nuclear Power Engineering Company，Beijing 100840，China）

The passive safety system of nuclear power plant relays on natural circulation for heat dissipation. However, the hydraulic pressure, flow resistance, and flow rate in the system will affect each other, which can easily cause flow instability and greatly reduce the corresponding CHF value. Therefore, the instability is one of the important research topics in the natural circulation thermal system. In this paper, a vertical round heating tube with an open outlet is tested under various heat fluxes and inlet subcooled temperatures. Through experimental results and theoretical analysis, the characteristics of geysering boiling and flow instability under natural convection conditions in the tube are studied. The results show that with the increase of heat flux, the system has four stages: initial state, low-frequency pulsation, high-frequency pulsation and stable natural circulation. Based on the experimental data, a prediction model of the unstable boundary is established. The predicted value and the experimental value are in good agreement, and the error is within ±10%.

Open system; Geysering boiling; Natural circulation; Instability boundary

TL33

A

0258-0918（2022）02-0372-09

2021-01-29

国家重点研发计划资助(2018YFB1900100)

孙运达（1996—），男，江苏连云港人，硕士，现主要从事热工水力相关方面研究

龚圣捷，E-mail: gsj@sjtu.edu.cn