核电厂安全壳中预应力的数值模拟

胡　钟，李宇琛，张映玲，薛　卫

核电厂安全壳中预应力的数值模拟

胡钟，李宇琛，张映玲，薛卫

（华龙国际核电技术有限公司，北京 100036）

在预应力混凝土安全壳结构计算中，预应力的计算分析以及模拟是十分重要的一部分。本文根据某核电厂安全壳预应力的布置情况，对预应力损失的分析过程进行了说明，并介绍了在安全壳数值模拟中用降温法模拟预应力的具体方法，同时采用修正系数对温降值进行修正，消除了传统一次降温法所产生的预应力损失，使预应力的模拟更为精确。此方法具有较高的通用性，供行业内工程设计人员参考。

安全壳；预应力；数值模拟；修正系数

预应力混凝土安全壳是防止放射性物质对环境产生污染的第三道安全屏障，它对维持机组正常运行，确保人员安全至关重要[1, 2]。预应力荷载是安全壳结构分析中最主要的荷载之一，预应力的精确模拟是安全壳结构分析中的一大技术难点，能否精确模拟预应力荷载效应直接关系到模型的计算精度。所以，此项工作是后续抗震分析和极限承载能力分析的基础和前提条件，其本身也是计算的重要环节。设计人员对其开展了大量的研究工作，2010年董占发等[3]通过对CPR1000堆型安全壳预应力的摩擦及锚固损失分析，证实了预应力在安全壳中的分布状况、损失规律将直接影响到安全壳的设计和安全性；2011年孟剑等[4]根据某核电厂预应力钢束的布置形式推导出了钢束的空间几何曲线方程，精确计算了各点预应力值并完成了加载工作；2013年孙锋等[5]根据某核电厂安全壳预应力的布置情况计算了5年打压试验时安全壳结构的有效预应力，并通过数值模拟进行了结构计算，验证了预应力系统初步设计的正确性和有效性。本文根据某核电厂安全壳预应力的布置情况，对预应力损失的分析过程进行了说明，并详细介绍了在安全壳数值模拟中用降温法模拟预应力的具体方法，同时采用修正系数对温降值进行修正，此方法具有较高的通用性，供工程设计人员参考。

1　安全壳结构模型简介

1.1　混凝土安全壳尺寸

某核电厂安全壳的几何尺寸如图1所示，-7.950 m以下为核岛厂房共用基础底板，-7.950～-2.600 m为安全壳底部截椎体，-2.600～43.700 m为安全壳筒身，标高43.700 m以上为半圆形穹顶，安全壳壁厚1.5 m，内侧半径为21.5 m。图中示意的安全壳外侧混凝土结构为非能动水箱。本次计算考虑设备闸门、人员闸门和应急闸门三个较大洞口，洞口位置尺寸以及扶壁柱的位置如图1所示。

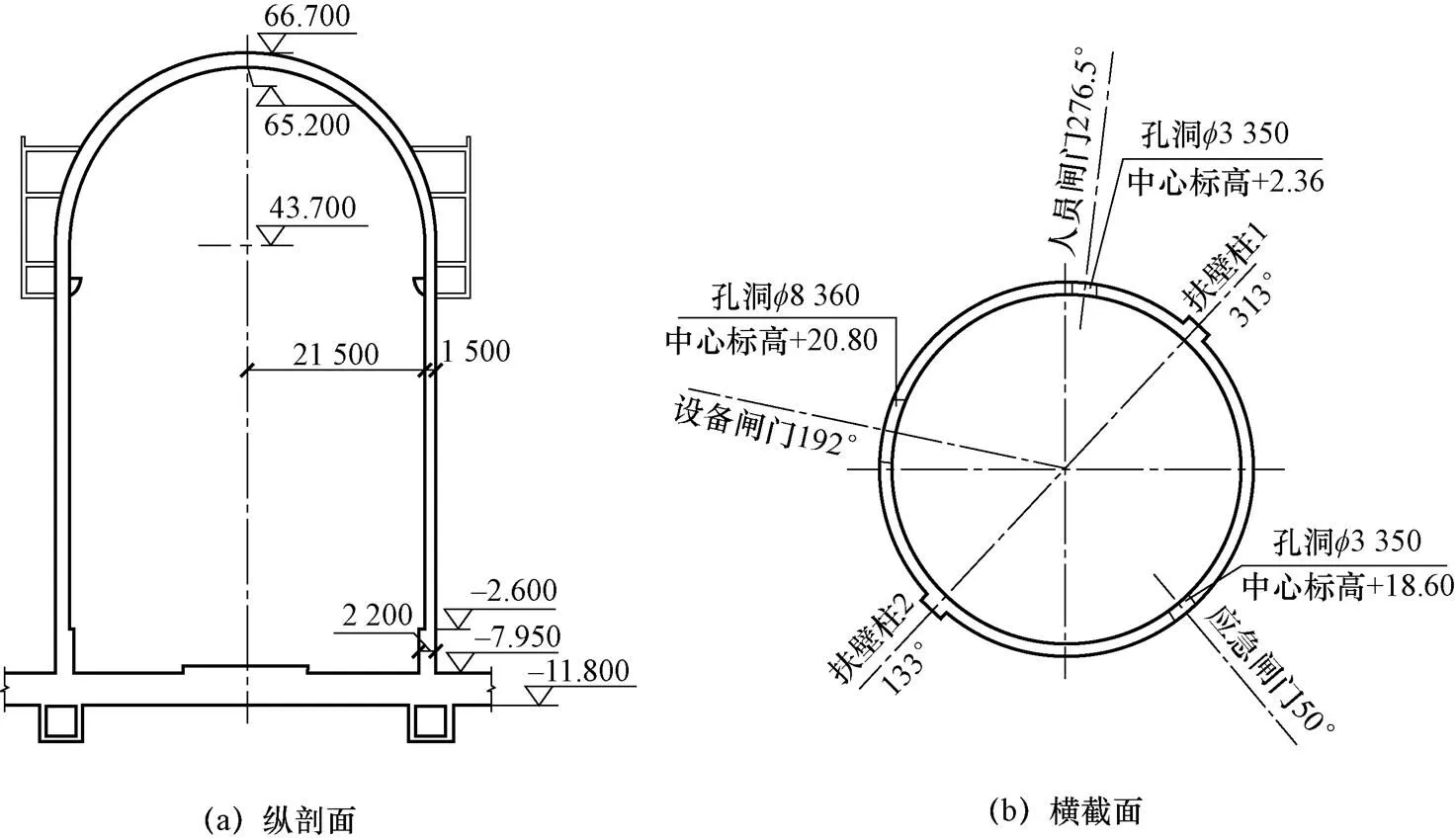
图1　安全壳几何尺寸

1.2　预应力系统

安全壳的预应力系统由水平环向预应力筋、竖向倒U型预应力筋和穹顶水平预应力筋组成。水平环向预应力筋间距500 mm，共103根；竖向倒U型预应力筋每隔2°布置一根，间距776 mm，共90根；穹顶水平预应力筋沿环向间距为500 mm，共35根，预应力筋的分布如图 2所示。

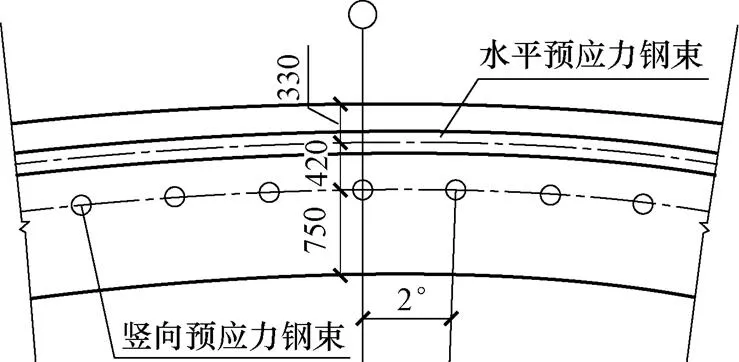
图2　预应力筋分布

2　数值模拟

预应力计算分析采用有限元分析软件Ansys/Workbench执行。建模形式采用分离式建模，将预应力筋和混凝土作为不同的单元分别建模。预应力筋模型和混凝土模型各自划分为足够精确的单元，使用约束方程法[6]采用ceintf命令建立连接，使预应力筋和混凝土变形协调一致。

2.1　混凝土

核电厂安全壳及外部水箱混凝土强度等级均为C60，弹性模量3.6×104MPa，线膨胀系数1.0×10-5/℃。有限元模型采用workbench默认的Mesh200实体单元，如图3所示。其中安全壳部分混凝土网格控制在500 mm，洞口局部位置采用更为精细化的网格划分方式，安全壳外挂水箱部分混凝土网格控制在300 mm。混凝土单元总数量为246 948个。安全壳底部设置为固定端。

图3　安全壳有限元模型

2.2　预应力筋

2.2.1预应力筋模型

预应力筋采用54束直径为150 mm的钢绞线组成，每根钢束截面积为8 100 mm2，预应力筋的弹性模量为1.95×105MPa，极限强度标准值ptk为1 860 MPa，预应力筋锚固时控制应力为0.8ptk（1 488 MPa），线膨胀系数取 1.2×10-5/℃。预应力筋采用LINK8杆单元进行模拟，考虑到预应力筋单元尺寸与混凝土单元尺寸的匹配以及便于计算各点预应力的损失值，对于水平环向预应力筋和穹顶水平预应力筋每隔2°划分一个单元，每根180个单元，标准段中的单元尺寸为791 mm；对于竖向倒U型预应力筋网格控制在800 mm。预应力筋单元总数量为43 583个。预应力筋的有限元模型如图4所示。

图4　预应力筋有限元模型

2.2.2预应力损失计算

本文采用NB/T 20303—2014《压水堆核电厂预应力混凝土安全壳设计规范》[7]计算预应力值，预应力损失考虑以下几项：

（1）预应力筋锚具变形和预应力筋内缩；

（2）预应力筋与孔道壁的摩擦作用；

（3）混凝土的弹性压缩；

（4）预应力筋的应力松弛；

（5）混凝土的收缩和徐变。其中，（1）～（3）属于瞬时损失，其数值在张拉完成后就已基本确定；（4）、（5）是与时间相关的预应力损失。预应力筋在各阶段的预应力损失值按表 1进行组合。计算有效预应力考虑60年的设计寿期。

表1　预应力损失值的组合

有效预应力计算是预应力分析工作的最大重难点，除水平环向不绕洞口的预应力筋外，其他预应力筋都需要根据具体情况进行逐根调整，以下展示了设备闸门洞口附近的预应力筋的有效预应力。设备闸门洞口附近的预应力筋如图5所示，洞口附近的水平预应力筋和倒U型预应力筋的有效预应力如图6所示。

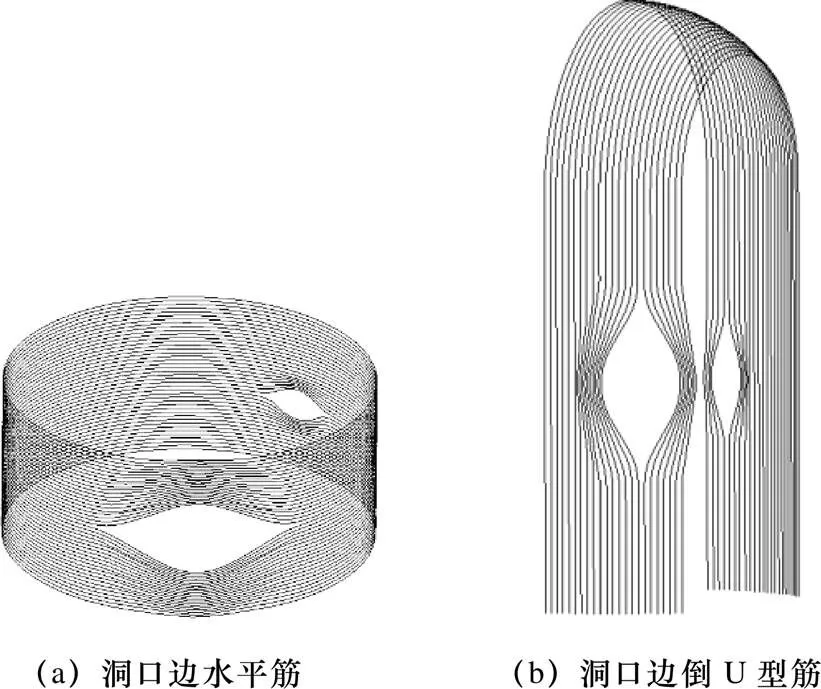
图5　设备闸门洞口附近的预应力筋模型

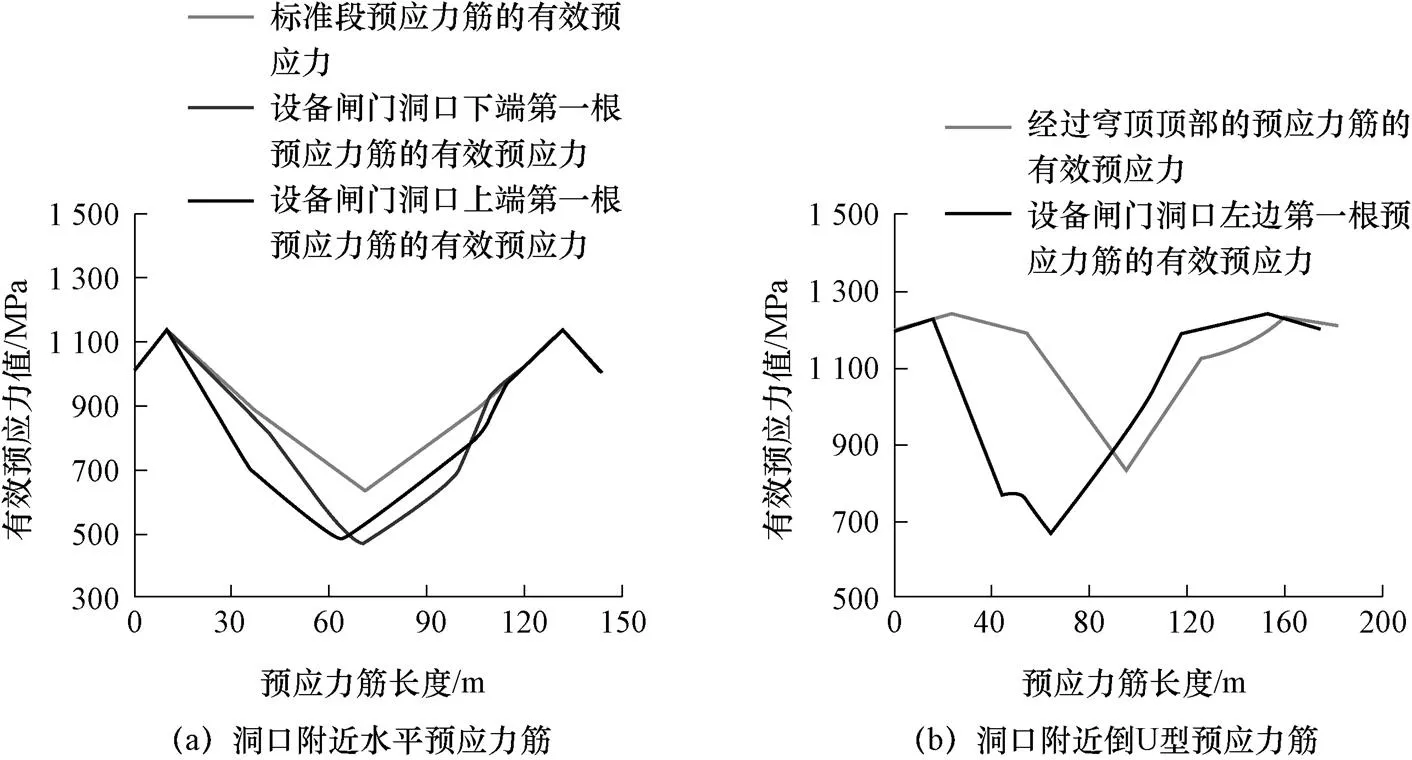
图6　设备闸门洞口附近预应力筋的有效预应力沿长度变化曲线

2.2.3预应力等效温度

降温法施加预应力即是在模型中的初始温度条件下给预应力单元节点施加一个温降值D，使杆单元发生收缩变形，引起的初始应变使杆单元产生预拉力，此预拉力用来模拟预应力筋中的预应力[8]，降温法的公式为：

式中：D——温降值；

——有效预应力；

——弹性模量；

——线膨胀系数。

给预应力单元节点施加的温度需考虑软件设置的环境温度，计算出的温降值D是一个相对温度差值，给节点施加的温度等于环境温度减去温降值。

2.2.4等效温度修正

计算出的有效预应力是后张法施工要达到的预应力水平，而降温法相当于先张法施工，即预应力会因为预应力筋与混凝土的共同变形而产生额外损失，为了能准确有效地模拟预应力作用，模型中最终施加的温度须在理论计算的基础上进行修正处理[9]。本次分析中采用的修正系数按以下方法确定：

（1）按照有效预应力值计算出各节点的温降值；

（2）将温度施加在预应力筋单元对应的节点上，在Workbench中进行试算；

（3）计算完成后，在后处理软件中提取每个预应力筋单元节点上的应力；

（4）用有效预应力除以本次计算得到的应力结果值，得到对应节点温降值的修正系数；

（5）将温降值乘以相应的修正系数完成修正过程，用修正后的温降值计算出的等效温度输入模型中再次计算，进行最终的预应力作用模拟。

表2列举出安全壳不同位置预应力筋节点的温度施加以及修正过程，并对修正前后的误差进行了对比。从表中计算结果可以看出，如果不采用修正系数进行迭代计算，则预应力误差约在2%～6%；采用修正系数进行修正后，得到的预应力筋应力值与期望得到的有效预应力值相差较小，误差基本控制在0.5%以内，大大的提高了预应力模拟的准确性。温降法修正前后产生较大误差的区域多集中在设备闸门洞口附近，此区域预应力布置紧密，变形大，因此所造成的预应力额外损失较其他区域更大。此方法还可以通过多次迭代计算直至达到精度要求，但从计算结果显示，一般只需迭代一次就能满足精度要求。

表2　降温法施加预应力

2.3　计算结果

以下计算结果分别显示了在预应力单工况作用下修正前后的安全壳和预应力筋的径向位移云图以及安全壳的应力云图，如图7～图9所示。为便于查看安全壳计算结果，图中隐去了安全壳外挂水箱的模型。由计算结果可知：

（1）预应力筋和混凝土安全壳实现了变形协调。安全壳筒身部位变形较为均匀，洞口周围变形较大。

（2）修正前安全壳最大径向位移为6.66 mm，修正后最大径向位移为7.29 mm，最大径向位移均出现在设备闸门洞口附近同一位置处，洞口周围由于刚度削弱，且预应力筋布置紧密，因此变形较其他区域更大。最大径向位移修正后比修正前高出9%左右，这是由于降温法使预应力筋和混凝土发生变形而产生额外的预应力损失所致，修正后的结果符合实际情况。

（3）安全壳整体受力均匀，修正前和修正后混凝土最大压应力均出现在设备闸门洞口附近同一位置处，修正后的压应力约高出修正前6%作用。除洞口周边外，大部分区域压应力均控制在25.8 MPa以内。

图7　修正前预应力作用下安全壳的径向位移图

图8　修正后预应力作用下安全壳的径向位移图

图9　预应力作用下混凝土安全壳的应力云图

3　结论

本文针对某核电厂安全壳预应力系统，采用Ansys/Workbench有限元分析软件进行了数值模拟，主要研究结论包括：

（1）采用约束方程建立预应力筋和混凝土模型的连接，可以有效模拟预应力混凝土结构，预应力筋和混凝土变形协调一致。

（2）降温法可以有效模拟预应力作用。但采用一次温降值直接模拟预应力效应会产生额外的预应力损失，损失值大约为2%～6%。

（3）对有效预应力进行计算迭代和修正后，采用得到的最终温降值进行预应力效应模拟，误差基本控制在0.5%以内。该方法大大的提高了预应力模拟的准确性，满足工程设计的要求。

［1］ 林诚格，赵瑞昌，刘志弢．安全壳在事故情况下的完整性分析［J］．核科学与工程，2010，30（2）：181-192．

［2］ 薛志成，李卫庆，裴强，等．预应力对核安全壳结构模态特性及抗震性能的影响［J］．沈阳建筑大学学报：自然科学版，2016，32（1）：87-97．

［3］ 董占发，赵超超．核电厂安全壳预应力摩擦及锚固损失分析［J］．预应力技术，2010，78（1）：24-29．

［4］ 孟剑，杨景龙．安全壳极限承载力中预应力的数值模拟［J］．工业建筑，2011，41（1）：127-131．

［5］ 孙锋，潘蓉，王璐，等．设计基准内压下混凝土安全壳的有效预应力作用研究［J］．核安全，2013，12（3）：21-25．

［6］ 李振宝，林树潮，等．布置倒U型与倒V型预应力筋的安全壳受力性能分析［J］．工业建筑，2016，46（12）：62-66．

［7］ 国家能源局．压水堆核电厂预应力混凝土安全壳设计规范：NB/T 20303—2014［S］．2014．

［8］ 赵超超，李忠诚，董占发．CPR1000 安全壳结构极限承载能力分析［J］．计算机辅助工程，2013，22（2）：393-399．

［9］ 付永强，张小水，胡成．预应力混凝土结构施加预应力的Ansys模拟［J］．工程与建设，2008，22（6）：784-786．

Numerical Simulation of the Pre-stress in the Containment of Nuclear Power Plant

HU Zhong，LI Yuchen，ZHANG Yingling，XUE Wei

（Hualong Nuclear Power Technology Co.，Ltd.，Beijing 100036，China）

The analysis and simulation of the pre-stress is a very important part in the calculation of the pre-stressed concrete containment structure. In this paper，the analysis process of the pre-stress loss is explained according to the arrangement of the pre-stress in the containment of a nuclear power plant. The temperature drop method of simulating the pre-stress in the numerical simulation of the containment is introduced. The correction coefficient is used to correct the temperature drop value，which eliminates the pre-stress loss caused by the traditional one-time temperature drop method and makes the simulation of the pre-stress more accurate. This method is more general as a reference for engineering designers in the industry.

Containment；Pre-stress；Numerical simulation；Correction coefficient

T364+.3

A

0258-0918（2022）02-0365-07

2021-01-29

胡 钟（1985—），男，安徽无为人，高级工程师，现从事反应堆厂房结构设计相关研究