恶意模型下保密判定点与凸多边形的包含关系*

刘 新, 张瑞玲, 徐 刚, 陈秀波

1. 内蒙古科技大学信息工程学院, 包头 014010

2. 北方工业大学信息学院, 北京 100144

3. 北京邮电大学网络与交换技术国家重点实验室信息安全中心, 北京 100876

1 引言

随着区块链、大数据、人工智能等新兴技术在社会各领域融合创新快速发展, 数据信息不断丰富, 人们的生活得到了许多便利. 然而在享有这些数据资源的同时, 信息保密也成为了人们的关注焦点. 安全多方计算是用于解决隐私数据协同计算的重要工具之一, 受到广泛关注[1,2].

最早的安全多方计算问题是由计算机科学家姚期智教授提出的百万富翁问题(millionaires’ problem)[3]. 随后Goldreich、Lindell 等[4,5]研究学者对其进行了深入的研究, 安全多方计算研究领域不断扩展, 其中包括保密数据挖掘、保密的计算几何和集合问题、保密的科学计算等[6,7]. 这些研究不断地推动安全多方计算向前发展, 切实解决了许多实际问题.

安全计算几何问题是研究安全多方计算的一个重要分支, 而点与凸多边形关系判断问题是一个典型的安全多方计算几何问题, 应用领域广泛. 但其研究方案并不多见, 仅有的研究方案也是在半诚实模型下设计的[8,9], 不能抵抗恶意敌手的攻击.

本文设计了恶意模型下的点与凸多边形包含问题的判定协议, 贡献如下:

(1) 本文首先研究了半诚实模型下的点与凸多边形关系判定协议[8], 并分析了可能存在的恶意行为;

(2) 在半诚实协议的基础上, 利用Paillier 加密算法, 借助零知识证明和分割-选择等密码学工具, 设计了恶意模型下的保密判定点与凸多边形包含问题协议;

(3) 利用理想-实际范例方法证明在恶意模型下协议的安全性, 并分析对比恶意模型下协议的优越性.

2 相关工作

点和凸多边形关系的保密判定, 是指在保护两方隐私的情况下, 判断一方的点是否包含在另一方的凸多边形中. 这个问题在现实生活中有着非常广泛的应用, 如保密的范围查询、保密定位搜索等.

文献[8] 针对判断点与凸多边形的位置关系, 首先将点与凸多边形的包含问题转化为计算三角形的面积问题, 然后借助内积协议从而设计了点与凸多边形的关系判定协议. 然而, 该协议是在半诚实模型下提出的, 不能抵抗恶意敌手的攻击.

文献[9] 首先在OTn1和矢量几何的基础上, 设计了一种茫然安全点与线位置关系判断协议. 然后, 将此协议作为基础协议, 并结合二分检索法提出了点与凸多边形位置判定协议. 该协议也是在半诚实模型下进行设计的, 不能抵抗恶意敌手的攻击.

文献[10] 将半诚实模型下的百万富翁问题解决方案改造成恶意模型下安全计算协议, 并用理想-实际范例证明了协议的安全性. 该文献在恶意模型下解决了百万富翁问题, 能够抵抗恶意敌手的攻击, 但与本文场景不同.

文献[11] 首先设计了一种新的编码方法, 采用ElGamal 同态加密, 在半诚实模型下设计了多个数据相等的保密判定协议, 并进一步利用比特承诺、零知识证明等方法设计出了恶意模型下多数据相等问题判定协议. 但与本文解决问题的场景不一致.

文献[12] 采用Paillier 加密算法设计了两个有理数相等的保密判定协议, 并且最后给出了恶意模型下的有理数相等保密判定协议. 该文虽然可以抵抗恶意敌手的攻击, 但与本文解决的问题不一致.

现有抗恶意敌手的安全多方计算协议与本文研究的应用场景不同, 不能解决点与凸多边形的保密判定. 而目前保密判定点与凸多边形的协议大多又是在半诚实模型下提出的, 不能抵抗恶意敌手的攻击, 而且存在隐私泄露、甚至可能出现判断错误等问题.

针对上述不足, 本文设计了恶意模型下保密判断点和凸多边形关系协议, 并与现有协议进行对比分析,本协议效率保持高效, 且可抵抗恶意攻击.

3 预备知识

3.1 Paillier 加密算法

3.2 零知识证明

3.3 分割选择

分割-选择(cut-and-choose) 是一个重要密码学工具. 在大多数有恶意参与者参与的协议中, 将采用分割-选择方法. 所谓的分割-选择方法[15]是一方构造并发送大量的电路, 另一方随机的选出其中一半的电路, 并要求对方打开电路检查电路的正确性, 之后对没有打开的另一半电路进行保密计算. 例如:

3.4 恶意模型的安全性定义

在恶意模型下, 广为接受的可证明安全方法为理想-实际范例. 所谓理想-实际范例就是协议具有与理想模型下一样的安全性.

理想协议:Alice 拥有信息x, Bob 拥有信息y, 要计算函数f(x,y) = (f1(x,y),f2(x,y)). 在协议结束后, 双方分别只得到f1(x,y) 和f2(x,y), 而得不到其他任何信息. 在执行协议计算函数的过程中, 双方会借助可信的第三方(trusted third party, TTP) 来计算. 具体情形如下:

(1) Alice 和Bob 分别拥有x、y, 发给TTP, 诚实的参与者会给TTP 提供真实的输入, 而恶意的参与者会根据自己的信息来提供虚假的输入x′或y′.

(2) 当TTP 获得输入信息(x,y) 后会计算f(x,y), 并将f1(x,y) 发送给Alice, 反之发送特殊符号⊥.

(3) 如果Alice 是恶意参与者, Alice 收到信息f1(x,y) 不再理会TTP, 则TTP 会给Bob 发送⊥;反之给Bob 发送f2(x,y).

在理想协议中, 双方除了可以获得各自的结果外而得不到其他任何信息. 如果在恶意模型中, 我们执行的结果与理想模型下得到的结果一样, 即可以证明恶意模型下协议是安全的. 值得注意的是, 恶意模型下的协议在执行时应至少有一方是诚实的, 否则将不能保证协议是安全可行的. 在文献[10] 中给出其安全性定义.

3.5 点与凸多边形包含问题的描述与转化

(1) 问题描述

Alice 拥有点P0(x0,y0), Bob 拥有多边形G, 其中G的顶点用Gi(xi,yi) 表示,i= 1,2,··· ,n.P0与G有两种位置关系, 即P0⊂G或者P0̸⊂G.

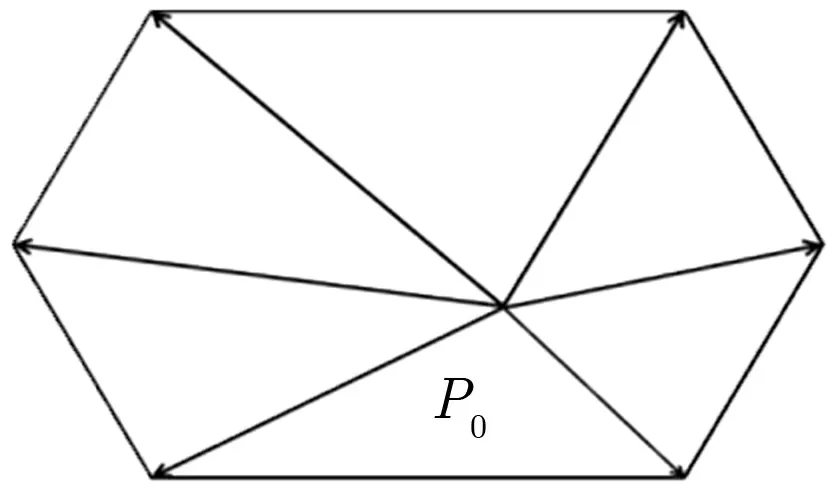
图1 点在凸多边形内部Figure 1 Points inside convex polygon

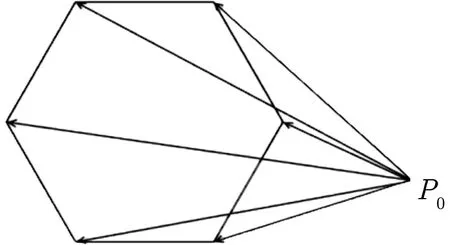
图2 点在凸多边形外部Figure 2 Points outside convex polygon

(2) 转化规则

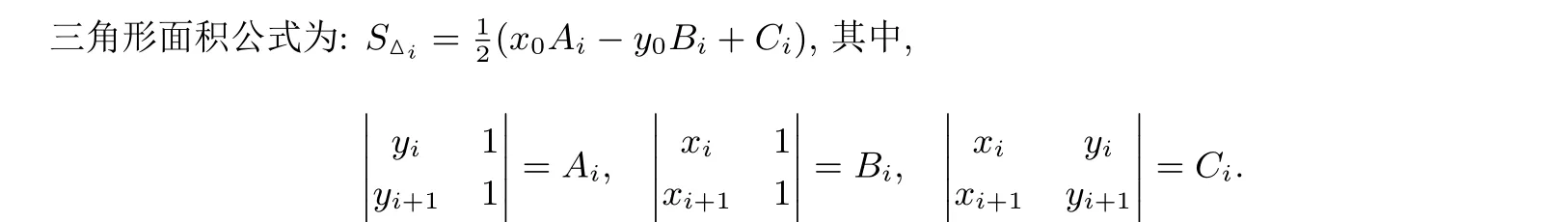
4 半诚实模型下的协议

半诚实模型下的协议是设计恶意模型协议的基础, 恶意模型协议是根据半诚实模型协议中可能出现的恶意行为来设计的, 因此分析在半诚实模型下的协议及其安全性是极其重要的. 在文献[8] 中, 作者巧妙地将点与凸多边形的包含问题转化为面积判等问题, 而在计算三角形面积时, 利用内积的性质并调用了内积协议, 即〈X,Y1〉+〈X,Y2〉=〈X,Y1+Y2〉. 具体协议如下:

协议1 半诚实模型下判断点与凸多边形的包含关系输入: Alice 拥有点P0(x,y), Bob 拥有凸多边形G, G 有n 个顶点, 其中i = 1,2,··· ,n.输出: P0 ⊂G 或P0 ̸⊂G.1 Bob 从G 上选取相邻的顶点Gi, Gi+1, 获得Gi(xi,yi), Gi+1(xi+1,yi+1), 计算:Ai =■■■■■yi1 yi+1 1■■■■■, Bi =■■■■■xi1 xi+1 1■■■■■, Ci =■■■■■xiyi xi+1 yi+1■■■■■,即获得向量Yi = (Ai,Bi,Ci), 并计算得到∑n i=1 Yi.2 Alice 计算得到向量X = (x0,−y0,1), 并发送给Bob.3 Bob 调用内积协议得到〈X,∑n i=1 Yi〉, 那么, n 个三角形的面积之和为:n∑S△i = 1 n∑⟨n∑⟩〈X,Yi〉 = 1 X,Yi .i=1 2 i=1 2 i=1 4 Bob 计算G 的面积S凸多边形与∑n i=1 S△i 比较. 当S凸多边形=∑n i=1 S△i, P0 ⊂G; 否则P0 ̸⊂G.5 协议结束.

在协议1 中, 只有在Alice 和Bob 都是半诚实参与者的情况下, 协议才是安全的. 当Alice 或Bob 其中的一方是恶意的, 协议将不再安全, 需要改进协议使其对于恶意参与者也是安全的.

5 恶意模型下点与凸多边形包含问题的保密判断协议

解决思路: 分析在半诚实模型协议中可能出现的恶意敌攻击行为, 根据其攻击的缺口, 设计相应协议来使得恶意敌手无法进行攻击或被发现. 协议1 中可能出现的恶意行为:

(1)在协议1 的第1、2 步,Alice 和Bob 是根据自己拥有的数据来进行计算的. 在协议的第2 步Alice可能不会将正确的信息发送给对方, 这种情况我们将不予考虑. 当面对提供不真实输入的情况时, 在理想模型下也无法解决. 因此, 理想情况下都不可避免的情形, 在恶意模型下我们也不会考虑该种情况.

(2) 协议1 的第3 步是Bob 调用内积协议, 这样Bob 就拥有了主动权, 可以计算n个三角形的面积和来与自己的凸多边形面积来进行比较, 这样对Alice 很不公平.

(3) 协议1 在第4 步存在恶意敌手的攻击行为, 即Bob 可能不会将正确的计算结果告诉Alice, 而此时Bob 已经知道了点与凸多边形的位置关系, 与此同时Alice 不会获得结果或者获得一个错误的结果.

为了防止以上恶意行为, 利用Paillier 加密算法, 借助零知识证明和分割-选择等密码学工具, 改进协议1 来抵抗恶意敌手的攻击, 最终双方一起来验证结果. 为了提高效率, 本文巧妙的将点与凸多边形关系判断问题转换为两数判等问题, 来设计恶意模型下的协议.

5.1 具体协议

在恶意模型下判断点与凸多边形的包含关系, 我们已经巧妙地将点与凸多边形的问题, 转化为面积判等的问题, 即n个三角形的面积之和是否与凸多边形的面积相等的问题, 其中Q1代表n个三角形的面积之和,Q2代表凸多边形的面积. 具体协议如下所示.

协议2 恶意模型下判断点与凸多边形的包含关系输入: Alice 拥有点P0(x0,y0), Bob 拥有凸多边形G, G 有n 个顶点Gi(xi,yi), 其中i = 1,2,··· ,n.准备阶段: Alice 和Bob 分别生成自己的Paillier 密码系统的公钥(ga,Na), (gb,Nb), 私钥λa、λb, 并计算u = gaλa mod N2a, v = gbλb mod N2b, 交换(ga,Na,u) 和(gb,Nb,v).输出: P0 ⊂G 或P0 ̸⊂G.1 Bob 在凸多边形G 上任选两个顶点Gi(xi,yi), Gi+1(xi+1,yi+1), 计算Ai =■■■■■yi1 yi+1 1■■■■■Bi =■■■■■xi1 xi+1 1■■■■■Ci =■■■■■xiyi xi+1 yi+1■■■■■;i=1 Yi, 然后将∑n i=1 Yi 发送给Alice.2 Alice 构造向量X = (x0,−y0,1), 然后调用内积协议得到〈X,∑n i=1 Yi〉, 从而计算n 个三角形的面积和Q1 = ∑n i=1 Q△i = 1 Bob 构造向量Yi = (Ai,Bi,Ci), 并计算∑n 2〈X,∑n i=1 Yi〉.3 Bob 知道自己的凸多边形G 的面积, 即Q2.4 Alice 和Bob 分别选择m 个随机数ai,bi(i = 1,··· ,m) 并用各自的Paillier 加密算法的公钥计算2∑ni=1〈X,Yi〉 = 1(Ci 1a,Ci2a) = (gaiQ1amod N2a,gaia mod N2a)(Ci 1b,Ci2b) = (gbiQ2bmod N2b,gbib mod N2b)1a,Ci2a), (Ci1b,Ci2b).5 借助分割-选择方法, Alice 从m 组(Ci并分别公布(Ci 1b,Ci2b) 中任选m/2 组(Ci1b,Ci2b), 在Bob 公布biQ2 后, Alice 验证gbiQ2 bmod N2b = Ci1b, 如验证通过, 则继续执行协议, 否则中止协议.6 Bob 从m 组(Ci 1a,Ci2a) 中任选m/2 组(Ci1a,Ci2a), 在Alice 公布aiQ1 后, Bob 验证gaiQ1 amod N2a =Ci 1a, 如果验证通过, 则继续执行协议, 否则中止协议.1a,Ci2a) 和(Ci1b,Ci2b) 中随机选择一个(Cj1a,Cj2a) 和(Cj1b,Cj2b),并选取a ∈Z∗b, b ∈Z∗a.8 Alice 计算Cb = Eb(abj(Q1 −Q2)) = (Cj 7 Alice 和Bob 分别从其余的m/2 组(Ci 2b)aQ1(Cj1b)−arNb1 mod N2b = gabj(Q1−Q2)b rNb 1 mod N2b, 并发送给Bob.9 Bob 计算Ca = Ea(aib(Q1 −Q2)) = (Ci1a)(Ci2a)−bQ2rNa2 mod N2a = gaib(Q1−Q2)a rNa2 mod N2a, 并发送给Alice.10 Alice 用λa 计算ma = Cλaa mod N2a, Bob 用λb 计算mb = Cλbb mod N2b, 并公布ma, mb.11 双方借助零知识证明来验证计算的正确性, Alice 证明logCama = loggaµ, Bob 证明logCbmb = loggbν, 如其中一方不能通过证明, 则为恶意参与者.12 如证明通过, Bob 计算L(ma)/L(µ) 得aib(Q1 −Q2), 继而得到ai(Q1 −Q2). 当ai(Q1 −Q2) = 0 时, 则Q1 −Q2 = 0, 即Q1 = Q2, P0 ⊂G; 否则P0 ̸⊂G.13 Alice 计算L(mb)/L(ν) 得abj(Q1 −Q2), 继而得到bj(Q1 −Q2). 当bj(Q1 −Q2) = 0 时, 则Q1 −Q2 = 0, 即Q1 = Q2, P0 ⊂G; 否则P0 ̸⊂G.14 协议结束.

5.2 正确性分析

5.3 安全性证明

以下是用理想-实际范例来证明协议2 是安全的.

在协议2 中, Alice 和Bob 在第1–3 步中主要是为了保密求出Q1和Q2,Q1和Q2作为进一步执行协议的输入数据, 这类似于理想模型下参与者的输入信息, 若发给TTP 输入信息有误, 将无法继续进行协议. 因此, 在恶意模型下也不会考虑输入信息错误的情况, 即在证明中将判断点与凸多边形的包含关系问题转化为这一问题, 因而我们以下将证明协议第4 步之后的安全性.

定理1协议2(记为Π) 在有恶意参与者的情况下是安全的.

证明:由定义1可知, 如果协议Π 要安全地计算时间函数, 则需要双方共同在实际协议中找到都认可的策略对¯A=(A1,A2) 使得与理想模型下的协议中的策略对¯B=(B1,B2) 不可区分, 即可证明协议的安全性.

为保证协议是安全可行的, 我们则必须保证至少一方是诚实的, 即: (1)A1是诚实的, 即A2是不诚实的; (2)A1是不诚实的, 即A2是诚实的.

首先证明第一种情况:A1是诚实的,A2是不诚实的.

当A1是诚实的, 执行协议Π, 则有:

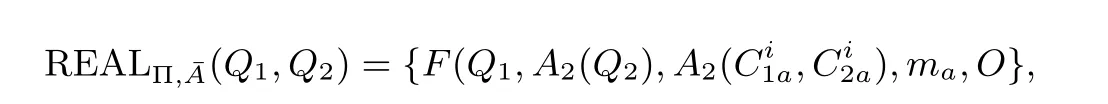
其中O是A2借助零知识证明收到的序列消息.

当A1是诚实的,A1会诚实的执行协议, 这时B1也就确定下来了. 我们只需要证明实际协议中的A2与理想模型下的B2是不可区分的, 为此我们要在理想模型中找到一个策略对 ¯B= (B1,B2) 的输出与实际模型下的REALΠ,¯A(Q1,Q2) 是不可区分的. 值得注意的是, 在执行协议的过程中,A2是实际的执行者,因此在证明的过程中, 我们必须根据A2的行为, 即A2(Q2) 来验证协议的正确性.

在模拟器B2执行协议过程中, 我们可以得到:

证明第二种情况:A1是不诚实的,A2是诚实的. 存在以下有两种情况:

(1) 当Alice 收到信息不再理会TTP 时, TTP 给Bob 将会发送⊥, 那么:

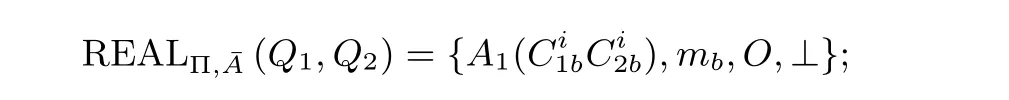
(2) 反之, TTP 给Bob 发送信息F2(A1(Q1),Q2), 那么:

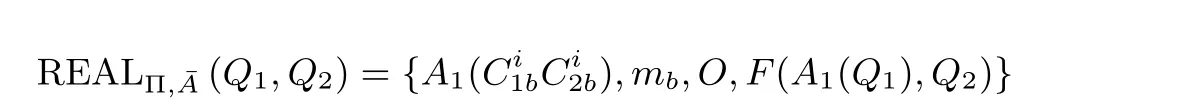
其中,O是A1借助零知识证明收到的序列消息.

当A2是诚实的,A2会诚实执行协议, 这时B2也就确定下来了. 我们只需要证明实际协议中的A1与理想模型下的B1是不可区分的, 为此我们要在理想模型中找到一个策略对 ¯B= (B1,B2) 的输出与实际模型下的REALΠ,¯A(Q1,Q2)是不可区分的. 值得注意的是, 在执行协议的过程中,A1是实际的执行者,因此在证明的过程中, 我们必须根据A1的行为, 即A1(Q1) 来验证协议的正确性.

在模拟器B1执行协议的过程中, 有以下两种情况:

(1) 当A1收到信息不再理会TTP 时, 得到:

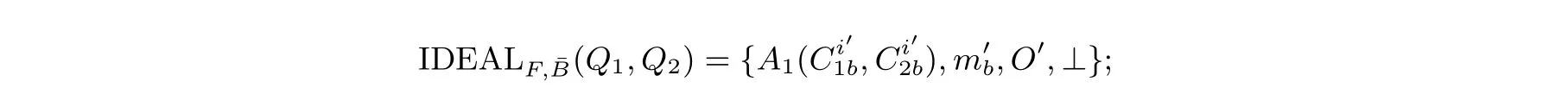
(2) 反之, 得到

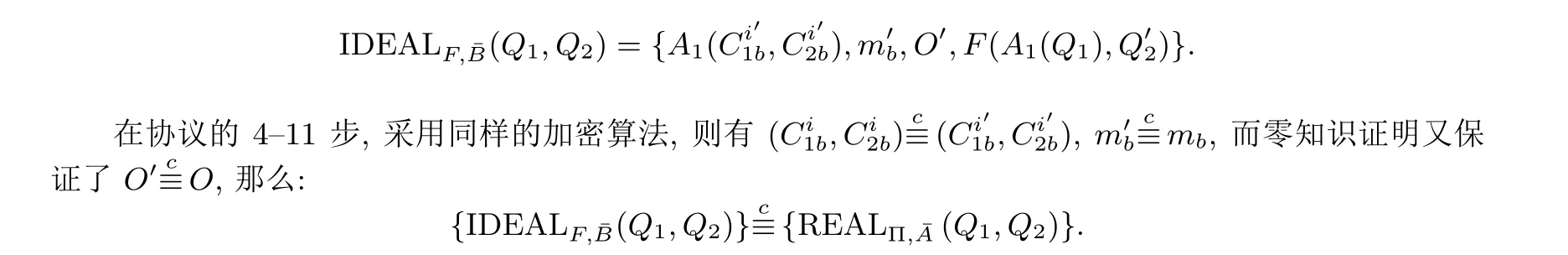
综合以上两种情况, 在理想模型中找到一个策略对 ¯B= (B1,B2) 的输出与实际模型下的REALΠ,¯A(Q1,Q2) 是不可区分的, 满足定义1. 因此, 协议2 在恶意模型下是安全的.

6 性能分析

6.1 整体性能对比

本文设计了恶意模型下点与凸多边形包含关系保密判定协议. 由于当下保密判定点与凸多边形包含关系的协议均是在半诚实模型下设计的, 而有些在恶意模型下的协议应用场景与本协议不同将无法比较.以下是本文协议与相关协议的整体性能比较, 如表1 所示.

表1 整体性能比较Table 1 Overall performance comparison

6.2 计算复杂度与通信复杂度

6.2.1 计算复杂度

为比较协议的计算复杂度, 此时假设所有方案调用的是同一个内积协议、同一个百万富翁协议、同一个OTn1协议, 且假设所有的基础协议各交互了3 轮. 本文在比较计算复杂度时, 将模乘运算作为衡量指标.

在文献[8] 中, 调用了一次内积协议, 则其总的计算复杂度为n; 文献[9] 中的协议调用了6 次借助茫然点线关系协议, 而茫然点线关系协议调用了一次OTn1协议、两次点积协议以及一次百万富翁协议, 则其总的计算复杂度为6·2n+24n+12; 文献[11] 采用ElGamal 加密系统, 并利用比特承诺函数, 使参与者要在上一个参与者之后要揭示剩余的承诺, 则其计算复杂度为mn+2(m+n); 文献[12] 采用Paillier加密算法, 其计算复杂度为b1+b2+λ.

在本文协议2 中, 第1–3 步是分别计算各自的面积Q1、Q2, 并没有采用任何加密算法, 因而其计算复杂度可以忽略不计; 第7–13 步已经将问题转化为SMP (socialist millionaires’ problem), 并调用了内积协议, 因而其总的计算复杂度为2(λ+N)+n. 具体比较见表2.

6.2.2 通信复杂度

在文献[8] 中, 进行了3 轮通信; 在文献[9] 中, 双方进行了12 轮通信; 在文献[11] 中, 进行了2m轮协议, 其中m代表参与的人数; 在文献[12] 中, 进行了4 轮通信; 在协议2 中进行了6 轮通信. 具体比较见表2.

表2 协议效率比较Table 2 Efficiency comparison of protocols

如表2 所示, 对于解决相同问题的文献[8], 计算复杂度比协议2 的计算复杂度稍好, 但不能抵抗恶意敌手的攻击; 在文献[9] 中调用了大量的基础协议, 计算量大大增加, 因而协议2 的计算复杂度较好. 因此, 相比于半诚实模型下的文献[8,9], 协议2 可以在保持高效的同时又可以抵抗恶意敌手攻击. 文献[11]和[12] 是在恶意模型下提出的协议, 其计算复杂度与参与者的输入位数有关, 且解决的问题、应用场景与本文协议是不同的. 就安全两方协议来说, 协议2 相比于其他的恶意模型下协议的效率要高.

值得注意的是, 恶意模型下的协议大多会借助分割-选择、比特承若、零知识证明等工具. 对此, 我们可以采用预处理或者服务外包来提高协议效率.

7 结论

研究点与凸多边形包含关系保密判定问题具有重要的应用前景, 如军事演习中一方军队想在另一方军队中演习, 但又不能因演习泄漏基地位置信息, 因此需要保密的判断演习地点是否在对方的范围内; 公司两方在不泄露具体商业位置时扩展业务, 也需要秘密判断其商务范围等等. 现有的点与凸多边形包含关系保密判定协议大多是基于半诚实模型提出的, 无法抵抗恶意敌手攻击. 本文利用Paillier 加密算法、零知识证明和分割-选择方法, 设计了恶意模型下点与凸多边形包含问题判定协议, 避免了不公平性, 又可抵抗恶意敌手攻击. 利用理想-实际范例证明了在恶意模型下该协议是安全的, 与现有协议相比更接近现实情况, 且保持高效, 具有实用价值.