简洁非交互零知识证明综述*
李威翰, 张宗洋, 周子博, 邓 燚
1. 北京航空航天大学网络空间安全学院, 北京 100191
2. 中国科学院信息工程研究所信息安全国家重点实验室, 北京 100093
1 引言
零知识证明由Goldwasser、Micali 和Rackoff[1]提出, 它是运行在证明者和验证者之间的一种两方密码协议, 可用于进行成员归属命题证明或知识证明. 零知识证明具有如下三个性质:
(1) 完备性, 用于描述协议本身的正确性. 给定某个陈述的有效证据, 如果证明者和验证者均诚实运行协议, 那么证明者能使验证者相信该陈述的正确性.
(2) 可靠性. 可靠性用于保护诚实验证者的利益, 使其免于恶意证明者的欺骗.
(3) 零知识性. 零知识性是指证明者能向验证者证明某个陈述的正确性而不泄露除正确性以外的其他任何信息.
零知识证明的三个性质使其具备了信任建立和隐私保护的功能, 具有良好的应用前景. 它不仅可以用于公钥加密[2]、签名[3]、身份认证[4]等经典密码学领域, 也与区块链[5]、隐私计算[6]等新兴热门技术的信任与隐私需求高度契合. 例如, 在区块链匿名密码货币(如Zcash1https://z.cash/.) 中, 零知识证明可在不泄露用户地址及金额的同时证明某笔未支付资金的拥有权[7]; 在区块链扩容(系列zk rollup 方案, 如zkSync2https://zksync.io/.) 中,链上的复杂计算需要转移到链下, 而零知识证明可保障该过程的数据有效性; 在匿名密码认证[8–10]中, 零知识证明可在不泄露用户私钥的同时证明拥有私钥, 从而实现匿名身份认证.
虽然针对通用NP 语言均可构造零知识证明[11], 但其落地应用仍存在若干问题. 仅以区块链为例,由于区块链往往具有低存储的需求且建立网络实时通信的开销较高, 适配于区块链的零知识证明通常需要具有简洁性和非交互的特点, 其中简洁性指证明的通信复杂度与陈述规模成亚线性关系, 非交互指证明者只需向验证者发送1 轮消息即可完成证明. 对于后者, 非交互可分别通过公共参考串模型(common reference string model, CRS)[12]和随机谕言模型(random oracle model, ROM)[13,14]实现. 然而对于简洁性, 尽管在1992 年Kilian[15]基于概率可验证证明(probabilistic checkable proof, PCP)[16,17]构造了简洁的交互式零知识证明, 而且Micali[18]基于ROM 将上述交互式证明转化为非交互证明, 但仅限于理论研究并难以实现.
直至基于二次算术程序(quadratic arithmetic program, QAP)/线性PCP (Linear-PCP) 的系列证明出现后, 零知识证明才得以落地实现. 该类零知识证明由Gennaro 等人[19]首次提出, 其中QAP 用于实现对待证明陈述的高效归约, Linear-PCP 用于构造高效信息论安全证明(即对于无穷算力的恶意敌手仍具有可靠性的证明). 该类零知识证明的通信复杂度为常数个群元素, 且验证复杂度仅与陈述的公共输入输出规模成线性关系. 除了理论上的研究和优化之外, 该类零知识证明在实际隐私保护应用中也大放异彩, 例如基于Pinocchio[20]的密码货币Pinocchio coin[21], 基于Ben-Sasson 等人协议[22]的密码货币Zcash, 基于Plonk[23]用于解决以太坊扩容问题的系列zk rollup 方案等.
然而, 即使是最高效的基于QAP/Linear-PCP 的简洁非交互零知识证明也存在若干问题. 在性能层面, 对于每个待证明陈述都需进行较长时间的预处理, 同时协议的实际证明开销较大. 在安全性方面, 协议所基于的难题假设是不可证伪(non-falsifiable) 假设[24,25], 假设本身的安全性难以完全保障; 并且为实现非交互和保障可靠性, 协议需要可信初始化(trusted setup), 即安全生成的CRS, 而这在去中心化的区块链中难以实现.
近年来的研究致力于从不同角度解决上述问题. 为解决证明生成效率不高的问题, 出现了实际证明速率较快的基于DEIP 的零知识证明[26–29]; 为解决底层假设通用性不足的问题, 出现了基于离散对数假设的零知识证明[30–32]和仅需单向函数存在的基于MPC-in-the-Head 的零知识证明[33–36]; 为解决初始化阶段可信需求高的问题, 出现了以削弱CRS 模型下的可信初始化设置为目标的抗颠覆的零知识证明[37–39]和CRS 可更新的零知识证明[23,40–42], 也出现了一系列不需预处理和可信初始化, 即启动阶段系统参数可独立公开生成的零知识证明(如STARK[43]、Bulletproofs[31]、Spartan[27]、Ligero[35]等).
简洁非交互零知识证明虽然在多个领域具有热门和广泛的应用前景, 但一方面零知识证明种类繁多,各类协议基于的原理驳杂, 性能侧重点也各不相同, 目前在一定程度上存在技术壁垒; 另一方面国内外针对简洁非交互零知识证明的相关综述较少, 缺乏系统的总结梳理(见第1.2 节), 因此有必要从通用构造方法、底层关键技术、协议性能表现、典型协议分析等角度, 对目前的简洁非交互零知识证明进行介绍, 为该领域的理论研究和应用实现提供一定参考.
1.1 本文贡献
本文详细梳理了现有的简洁非交互零知识证明, 主要贡献如下.
(1) 总结了简洁非交互零知识证明的通用构造方法(见图1). 构造方法分为四步, 分别是将待证明陈述转换为电路可满足问题(C-SAT 问题)、将电路可满足问题转换为易证明的语言(此步可省略,用虚线表示)、针对易证明的语言构造信息论安全证明和利用密码编译器将信息论安全证明转换为简洁非交互零知识证明.

图1 简洁非交互零知识证明的通用构造方法Figure 1 General method to construct succinct non-interactive zero-knowledge proof
(2) 基于上述通用构造方法, 分类研究了现有的简洁非交互零知识证明. 根据信息论安全证明的种类,主要分为基于PCP、Linear-PCP、交互式PCP(interacitve PCP, IPCP) 和交互式谕示证明(interactive oracle proof, IOP) 的零知识证明; 根据密码编译器应用的底层关键技术, 主要分为基于QAP、双向高效的交互式证明(doubly efficient interactive proof, DEIP)、内积论证(inner product argument, IPA) 和MPC-in-the-Head 的零知识证明. 表1 分别从信息论安全证明和密码编译器应用的底层关键技术两个角度, 总结了零知识证明, 涵盖了待证明陈述表示形式、协议性能、启动阶段参数能否公开生成等相关信息.
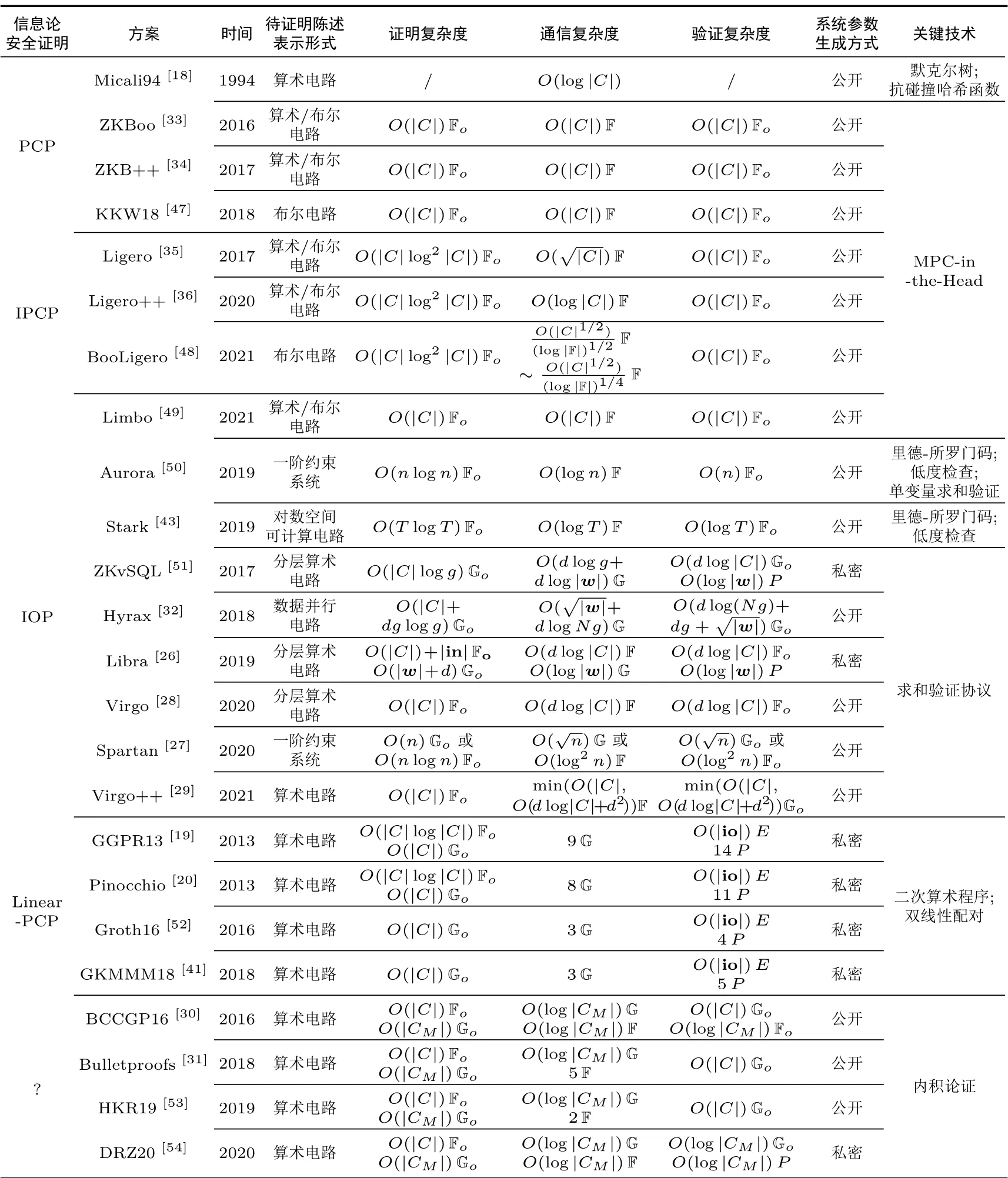
表1 基于不同角度分类的(简洁) 非交互零知识证明总结Table 1 Summary of (succinct) non-interactive zero-knowledge proof from different perspectives
(3) 总结了简洁非交互零知识证明的性能评价标准, 包括底层难题假设的通用性, 启动阶段系统参数能否公开生成, 证明、验证和通信复杂度, 是否抗量子等内容.
(4) 分析了未来简洁非交互零知识证明的研究热点和发展方向. 基于近年来简洁非交互零知识性证明的最新研究进展, 从通用构造、性能、安全性等方面给出若干可能的未来发展方向.
1.2 相关工作
简洁非交互零知识证明是实现区块链、隐私计算等场景下隐私保护的重要技术, 近几年对零知识证明尤其是简洁非交互零知识证明的综述研究主要包括以下内容.
Goldreich[44]梳理了零知识证明二十余年的发展情况, 介绍了交互式证明系统与论证、计算不可区分、单向函数等零知识证明涉及的核心概念, 探讨了零知识证明的标准定义及变种,如全局与黑盒模拟、诚实验证者零知识、计算与统计零知识、PPT 与期望多项式时间的模拟器等, 研究了零知识证明的证明能力, 并讨论了组合零知识证明、知识证明、非交互零知识证明等变种. Li 和McMillin[45]介绍了零知识证明的背景、重要概念及组合零知识证明等, 并详细给出了针对若干具体NP 问题的零知识证明, 包括三染色问题、图同构问题、哈密尔顿回路问题、背包问题、可满足性问题等. Mohr[46]研究了非交互零知识证
明在在密码学中的应用, 并重点探讨了Fiat-Shamir 认证协议是如何应用于零知识认证协议中的. 上述工作侧重于(非交互) 零知识证明理论层面的研究, 而本文同时着力于区块链等应用背景下简洁非交互零知识证明及典型协议的总结和研究.
Nitulescu[55]详细定义了zk-SNARK(zero-knowledge succinct non-interactive argument of knowledge), 并探讨了通用构造方法. Nitulescu 将zk-SNARK 分类为基于PCP、QAP、LIP 和PIOP (polynomial interactive oracle proof) 的零知识证明, 系统整理了各类证明的构造思路, 并总结了典型方案.Nitulescu 详细描述了基于QAP 的零知识证明的协议流程、底层难题假设及安全性等细节, 包括如何将C-SAT 问题归约为QAP 可满足问题、如何针对QAP 可满足问题构建Linear-PCP 等. 然而, 该工作着重于对zk-SNARK 的研究(对应于第5 章), 而本文除探讨zk-SNARK 外, 还详细对比研究了其他类别的简洁非交互零知识证明, 尤其是系统参数可公开生成的系列零知识证明. Morais 等人[56]对比了构造零知识范围证明的不同方法, 详细说明了Bulletproofs 中范围证明的实现细节, 但仅涉及对(零知识) 范围证明的研究. Sun 等人[57]研究并总结了在区块链背景下零知识证明的框架、模型及应用, 指出了目前区块链中零知识证明的应用现状、面临挑战及未来发展方向. 然而, 该工作不涉及对具体零知识证明方案的研究.
相比于前人的工作, 本文的亮点主要有二. 第一, 本文总结了简洁非交互零知识证明的通用构造方法,并基于该通用构造方法对现有简洁非交互零知识证明进行了分类. 分类共有两个维度, 一是信息论安全证明, 二是将信息论安全证明转换为简洁非交互零知识证明所基于的关键技术. 基于这两个维度, 本文较为深入地分类研究了现有的简洁非交互零知识证明, 总结了每一类证明的待证明陈述表示形式、协议性能等.第二, 本文基于上述分类维度详细梳理了每一类零知识证明的构建思路、优化方向及后续改进, 分析了安全性、复杂度及性能优缺点.
1.3 本文结构
本文结构如图2 所示. 第2 章介绍相关表示及全局定义. 第3 章介绍简洁非交互零知识证明的通用构造方法(图1) 及简洁非交互零知识证明的性能评价标准. 根据通用构造方法中信息论安全证明的不同,第4 章简要介绍基于概率可验证证明类的零知识证明, 主要包括概率可验证证明(PCP)、交互式概率可验证证明(IPCP)、交互式谕示证明(IOP) 和线性概率可验证证明(linear-PCP); 根据密码编译器应用的底层关键技术, 第5–8 章分别介绍基于二次算术程序(QAP)、双向高效交互式证明(DEIP)、内积论证(IPA) 和MPC-in-the-Head 的零知识证明, 详见图2(其中基于线性概率可验证证明和基于二次算术程序的零知识证明为同一类协议的两个维度). 第9 章介绍未来研究方向.
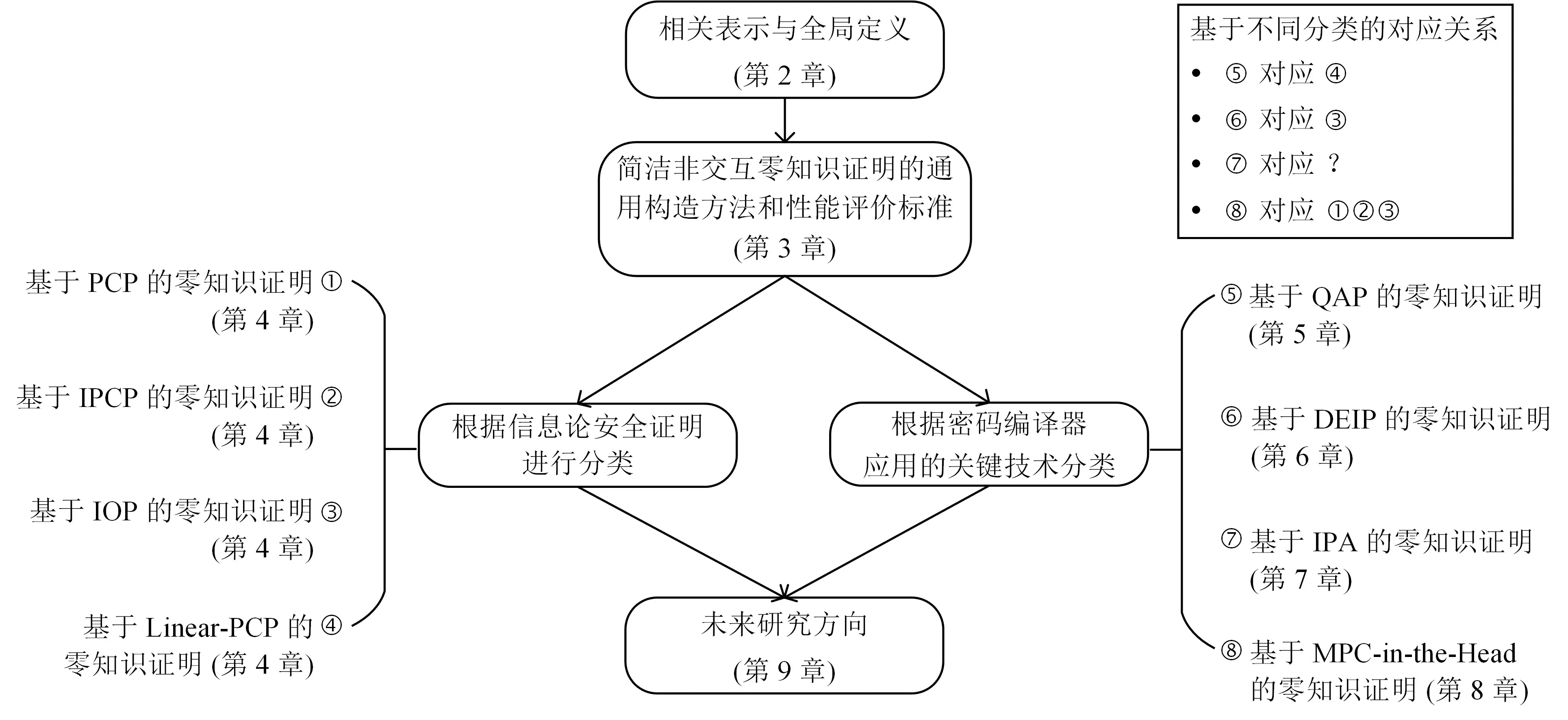
图2 本文结构Figure 2 Structure of this paper
2 相关表示与全局定义
2.1 相关表示
在本文中, 小写粗体字母表示向量, 例如a ∈F1×n表示域F 上维度为n的行向量(a1,a2,··· ,an),为表述方便, 常将F1×n简记为Fn.f(·)、g(·) 等表示多项式,f(·) 等表示向量多项式. 大写粗体字母(如A) 表示矩阵, 例如,A ∈Fm×n表示m行n列的矩阵且ai,j表示第i行、第j列的矩阵元素,Aa表示矩阵A与向量a的矩阵乘法. 本文用·表示乘法, 特别的,a·b=∑表示向量a与向量b的内积.⊙表示哈达玛积, 例如a ⊙b=(a1·b1,a2·b2,··· ,an·bn).y ←A(x,r) 表示算法A以x为输入、r为随机输入生成y的过程, 用y$←−S表示从集合S中均匀随机地挑选y,→表示函数映射关系, 用a?=b表示验证a是否等于b. 对于正整数n, [n] 表示集合{1,2,··· ,n}.
本文中的算法输入均包含安全参数λ. 如果对于任意的多项式p(·) 都存在常数c使得当λ>c时有negl(λ)< 1/p(λ), 则称negl(λ) 为对于λ的可忽略函数. 记f(λ)≈g(λ) 当|f(λ)−g(λ)|≤negl(λ). 用PPT 表示概率多项式时间(probabilistic polynomial time). 记Oλ(·) 为省略安全参数λ多项式因子的大O记法, 本文常省略λ. 本文常用的缩写词及含义对照表如表2 所示.

表2 缩略词及其含义对照表Table 2 Table for abbreviations and their meanings
2.2 全局定义
本节介绍本文涉及的主要基础知识, 第2.2.1 小节介绍电路及相关定义, 第2.2.2 小节介绍承诺及相关定义, 第2.2.3 小节介绍零知识证明及相关定义.
2.2.1 电路及相关定义
记算术电路(arithmetic circuit) 为C: F|x|+|w|→F|y|, 它由若干域上的加法门和乘法门组成. 布尔电路(Boolean circuit) 是算术电路的子类, 其仅有与门、异或门等布尔逻辑门, 变量取值仅为0 或1. 可以证明, 通过增加常数级别的电路门和深度, 任何布尔电路都可以转换为算术电路[61]. 不失一般性, 本文中出现的电路均为二输入电路(circuit with fan-in 2 gates). 记电路规模为电路中门的数量, 用|C| 表示,d表示电路深度,g表示电路宽度.
定义1(分层算术电路) 分层算术电路(layered arithmetic circuit) 是指可以分为d层、且任意层的电路门的输入导线全部位于上一层的算术电路.
可以证明, 通过增加电路深度级别的电路门, 任意的算术电路都可转换为分层算术电路[32].
定义2(电路可满足问题) 电路可满足问题(circuit satisfiability problem, C-SAT)是指给定电路C、电路的部分输入x(x可为空) 和电路输出y, 判断是否存在证据w(电路的另一部分输入, 视为秘密输入) 使得C(x,w)=y. 如无特殊说明, 本文中的零知识证明均是针对C-SAT 问题的.
针对布尔电路可满足问题的零知识证明可通过调用针对算术电路可满足问题的零知识证明高效构造(只需扩大域并增加对变量为0 或1 的约束即可), 反之, 尚不清楚是否有高效的转化方式.
定义 3(一阶约束系统[27,50]) 一个一阶约束系统(rank-1 constraint system, R1CS) 是七元组(F,A,B,C,io,m,n), 其中io表示公共输入输出向量,A,B,C ∈Fm×m,m ≥|io| + 1,n是所有矩阵中非零值的最大数目. 称R1CS 问题是可满足的当且仅当对于一个R1CS 组, 存在证据w ∈Fm−|io|−1使得(Az)⊙(Bz)=(Cz), 其中z=(io,1,w)T.
记n为R1CS 可满足问题的规模, 可以证明, 任意C-SAT 问题都可用R1CS 可满足问题表示[27],且n=O(|C|)[50].
R1CS 是高级语言编译器的常见目标程序[62,65]且形式较简单, 同时任意C-SAT 问题都可用R1CS可满足问题表示[27], 故有一些零知识证明[19,20]在应用实现时是先将C-SAT 问题转化为R1CS 可满足问题, 再针对R1CS 可满足问题构造的; 也有部分零知识证明[27,50]直接针对R1CS 可满足问题.
2.2.2 承诺及相关定义
定义4(承诺) 一个承诺方案(commitment scheme) 包含发送者和接收者两个参与方及三个PPT算法(Setup,Com,Open). 具体的, 算法Setup 用于生成承诺用公共参数pp. Compp定义了函数映射M×R→C, 其中M、R 和C 分别表示明文空间、随机数空间和承诺空间. Openpp算法定义了函数映射C×M×R→0/1. 具体的, 对于消息m ∈M 和随机数r ∈R, 承诺c的生成方式为c ←Compp(m;r),Open 算法为0/1←Openpp(c,m,r). 为表示方便, 本文常省略pp 和随机数r.
承诺有两个基本性质, 隐藏性(hiding) 和绑定性(binding). 其中, 隐藏性是指敌手获得承诺c后无法获知m的值, 绑定性是指一个承诺c在Open 阶段只能打开为一个值.
定义5(隐藏性) 计算隐藏性(computational hiding) 是指对于任意的PPT 敌手A, 有

对应的, 完美隐藏性(perfect hiding) 是将不等式(1)中的敌手A修改为无穷算力且“≤negl(λ)” 替换为“=0”.
定义6(绑定性) 计算绑定性(computational binding) 是指对于任意的PPT 敌手A, 有
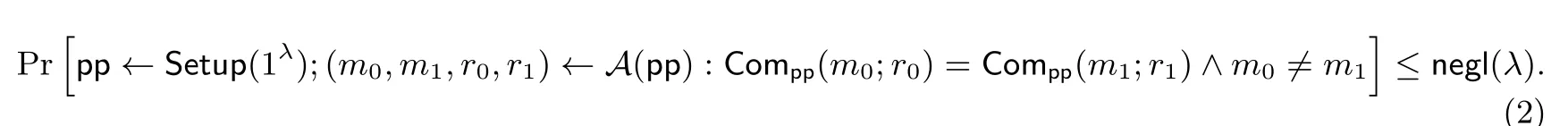
对应的, 完美绑定性(perfect binding) 是将不等式(2)中的敌手A修改为无穷算力且“≤negl(λ)” 替换为“=0”.
定义7(加性同态承诺) 加性同态承诺(additive homomorphic commitment) 是指具有加性同态性质的承诺, 即给定承诺Com(x;rx) 和Com(y;ry), 存在运算⊕, 满足

定义8(Pedersen 承诺[71]) Pedersen 承诺的明文空间、随机数空间和承诺空间分别为M = R =Zq,C=Gq. Setup 算法生成公共参数, 即G 上生成元g、h, 其承诺和承诺打开算法为gxhr ←Com(x;r)和0/1←Open(Com(x;r),x,r).
容易证明, Pedersen 承诺具有完美隐藏性、计算绑定性和加性同态性质.
定义9(Pedersen 向量承诺) Pedersen 向量承诺是对定义8的自然扩展, 其明文空间、随机数空间和承诺空间分别为M =, R = Zq, C = Gq. Setup 算法生成公共参数, 即Gnq上生成元g=(g1,g2,··· ,gn) 和Gq上生成元h, 向量承诺的承诺和打开承诺算法分别为
•c=gmhr ←Com(m;r). 承诺算法以消息m和随机数r为输入, 输出承诺c=gmhr.
• 0/1←Open(c,m,r). 承诺打开算法以承诺c、消息m和随机数r为输入, 验证承诺正确性.
2.2.3 零知识证明及相关定义
本小节介绍零知识证明, 并给出若干相关概念的简要定义.
给定二元关系R:{0,1}∗×{0,1}∗→{0,1}, 记语言L(R) 为集合{x:∃ws.t.R(x,w)=1}. 称一个语言L(R) 是NP 语言当如下两个条件成立:
(1)|w|=poly(|x|).
(2) 给定任意的x、w, 存在多项式时间算法能够高效判定R(x,w)?=1.
记〈A,B〉为一对交互式图灵机. 记〈A(y),B(z)〉(x) 为在A、B的随机输入带均匀独立选取, 公共输入为x,A的辅助输入为y,B的辅助输入为z时, 图灵机B与图灵机A交互后输出的随机变量.
定义10(交互式证明系统[1,72]) 给定二元关系R及其对应语言L(R), 则针对该语言的交互式证明系统(interactive proof system) 是〈P(y),V(z)〉, 其中图灵机P、P∗(也被称为证明者) 可以为无穷算力的, 图灵机V(也被称为验证者) 是PPT 的.〈P(y),V(z)〉满足如下两个性质.
•完备性(completeness): 对于任意的x ∈ L(R), 存在y, 使得对于任意的z ∈ {0,1}∗,Pr[〈P(y),V(z)〉(x) = 1]≥1−negl(|x|). 完美完备性(perfect completeness) 是指上述概率等于1.
•可靠性(soundness): 对于任意的x/∈L(R), 任意的恶意证明者P∗, 任意的y,z ∈{0,1}∗, 有Pr[〈P∗(y),V(z)〉(x)=1]≤negl(|x|).
定义11(交互式论证[72,73]) 交互式论证与交互式证明系统的区别在于, 论证可靠性定义中恶意证明者P∗被限制为PPT 的图灵机. 此外, 通常也限制完备性中的P为PPT 的[72, §4.8.1]. 具体的, 给定二元关系R及其对应语言L(R), 则针对该语言的交互式论证(interactive argument) 是〈P(y),V(z)〉,其中图灵机P、P∗和V均是PPT 的. 与证明系统类似,〈P(y),V(z)〉也具有完备性和可靠性.
零知识证明是具有零知识性的交互式证明系统或论证, 零知识性的直观含义是当以满足x ∈L(R) 的x为公共输入时, 任何在与P交互后高效计算出的信息也都可仅根据x高效计算得出(此时没有交互).

其中计算不可区分是指对于所有的概率性算法D(运行时间受poly|x| 限制)、所有的多项式p(·)、所有的z ∈{0,1}∗, 有

定义13(诚实验证者零知识[72]) 诚实验证者零知识(honest verifier zero-knowledge) 是指模拟过程中的验证者是按照事先确定好的协议步骤运行的. 给定二元关系R及其对应语言L(R), 令〈P,V〉是针对该语言的交互式证明系统(论证), 如果存在一个期望PPT 的模拟器S使得{viewPV(x,z)}x∈L(R) 和{S(x,z)}x∈L(R)这两个随机变量族是计算不可区分, 则称该证明系统(论证) 是诚实验证者计算零知识的.
定义14(知识论证[74]) 知识论证(argument of knowledge) 指具有知识可靠性的论证. 给定一个多项式时间内可判定的二元关系R及其对应的NP 语言L(R), 知识可靠性是指对于任意的PPT 敌手P∗, 都存在期望PPT 的提取器E, 使得对于L(R) 及任意的陈述x、w′, 如果有Pr[w′←P∗(x) :〈P∗(w′),V(z)〉(x) = 1]≥1/p(|x|), 其中p(·) 为某个多项式, 则有Pr[w′←EP∗(x) :R(x,w′) = 1]≥1/p(|x|)−negl(|x|).
本文中部分论证[30–32,53,54]援引的知识可靠性为统计意义的证据扩展可仿真性(statistical witnessextended emulation)[75].
定义15(公开抛币) 如果验证者在一个证明(论证) 的交互过程中发送的信息是公开抛币的直接结果, 则称该证明(论证)〈P,V〉是公开抛币(public coin) 的.
定义16(简洁性[25]) 对于一个交互式论证, 如果P和V之间的通信复杂度不超过poly(λ)(|x|+|w|)o(1),则称该论证〈P,V〉为简洁(succinct)的;如果通信复杂度不超过poly(λ)(|x|+|w|)c+o(|x|+|w|),则称论证为略显简洁的(slightly succinct), 其中c为某个小于1 的常数. 本文将简洁和略显简洁的零知识证明统称为简洁零知识证明.
基于标准假设[24](敌手仅受可用时间和算力限制) 无法实现简洁且具有统计级别可靠性的证明系统[76]. 如无特殊说明, 本文涉及到的所有具体零知识证明协议均是零知识论证或零知识知识论证, 为叙述方便, 本文将非交互零知识知识论证(non-interactive zero-knowledge argument of knowledge) 简记为NIZKAoK.
Σ协议[77]给定二元关系R及其对应语言L(R), 则针对该语言的Σ 协议是公开抛币的诚实验证者零知识论证, 其有以下三步.
• 承诺阶段: 证明者P向验证者V发送承诺a.
• 挑战阶段:V向P发送随机挑战e.
• 响应阶段:P向V发送响应函数f(w,r,e), 其中f是某公开函数,w是证据,r是随机数.
Σ 协议具有完备性、特殊知识可靠性和诚实验证者零知识性. 其中特殊知识可靠性(s-special soundness) 是指给定对于任意的陈述x及s个接受副本{(a,ei,zi)}i∈[s],x所对应的证据w可被高效提取.
非交互零知识证明交互式证明需要证明者和验证者时刻保持在线状态, 而这会因网络延迟、拒绝服务等原因难以保障. 而在非交互零知识证明中, 证明者仅需发送一轮消息即可完成证明. 然而, 在标准假设下已证明无法构造针对非平凡语言的非交互零知识证明系统[78], 因此必须引入新的假设. 目前主流的非交互零知识证明的构造方法有两种, 一是基于CRS 模型实现的, 二是基于ROM 并利用Fiat-Shamir 启发式实现的.
CRS 模型由Blum、Feldman 和Micali[12]提出, 其假设存在一个证明者和验证者可获得的由可信第三方生成的公共字符串, 其可由MPC 生成[79,80]. 本文中基于QAP 的零知识证明就是基于CRS 模型实现非交互的, 该类证明也被称为zk-SNARK[25,58,81], 其通信量为常数个群元素, 验证复杂度可通过预处理达到常数次配对运算.
然而, zk-SNARK 存在两个较为严重的问题, 一是需要可信初始化用以预处理, 二是基于非可证伪假设才是安全的. 对于问题一, 虽然Feige、Lapidot 和Shamir[82]基于单向函数存在的假设构造了同一个CRS 可用于证明多个陈述的非交互零知识证明, 但为实现更低的通信量和验证计算开销, 在绝大多数zk-SNARK 中CRS 都是与陈述相关的. 也就是说, 在给定待证明陈述后, 需先由可信第三方先进行相应预处理. 预处理虽然使得亚线性甚至常数级别的验证复杂度成为了可能(在无预处理情况下验证者读取陈述就会导致线性级别的验证复杂度), 但对于每个陈述都进行预处理也会带来较大的计算开销. 对于问题二, Gentry 和Wichs[25]从理论上证明了基于可证伪假设无法构造zk-SNARK. 可证伪假设是指可用敌手和高效挑战者之间的游戏模型描述的假设, 在游戏结束时, 挑战者能够高效判断敌手是否攻击成功. 常见的标准假设, 如单向函数存在、离散对数假设等都属于可证伪假设.
在ROM[13,14]下, 验证者的随机挑战可由哈希函数的输出替代, 由此任何公开抛币的交互式零知识论证(如Σ 协议) 可转换为非交互零知识论证[54,83–85]. 在Σ 协议中, 证明者计算e ←RO(x,a) 并用该e替代验证者的随机挑战, 其中RO 代表随机谕言函数. ROM 是一种理想的密码学模型, 其假设协议的所有参与方都有访问请求一个理想随机谕示的权限, 该谕示在实际应用中通常启发地用哈希函数替代. 在ROM 下, 该类非交互零知识证明可基于标准假设实现. 本文中基于PCP、IPCP、IOP、DEIP、IPA 和MPC-in-the-Head 的零知识证明均是通过ROM 下的Fiat-Shamir 启发式实现非交互的.
定义17(Schwartz-Zippel 引理[86,87]) 若域F 上多项式p(x1,x2,··· ,xn) 度为d且不为零多项式,令集合S ⊆F, 则对于(y1,y2,··· ,yn)S, 有与n无关的以下概率关系成立

Schwartz-Zippel 引理可将针对多项式约束的证明转化为针对多项式上某一点的证明, 其能够在保障可靠性(但会带来一定误差) 的同时降低通信复杂度, 是构造简洁非交互零知识证明的重要技术支撑之一.
3 简洁非交互零知识证明的通用构造方法及性能评价标准
3.1 简洁非交互零知识证明的通用构造方法
简洁非交互零知识证明的通用构造方法如图1 所示, 简要介绍如下.
(1) 将待证明陈述归约为C-SAT 问题. 一方面C-SAT 问题是NPC 问题, 也就是说任意NP 问题都可在多项式时间内归约为C-SAT 问题,另一方面大多数实际问题都可用电路形式表达,故现有的简洁非交互零知识证明的待证明陈述表示形式大都为C-SAT 问题. 事实上, 也存在一系列的算术电路生成器, 可将格式化计算程序转化为算术电路, 例如Meiklejohn 等人[88]提出的ZKPDL和Ben-Sasson 等人[81]提出的TinyRAM.然而, 这些库的实际归约效果可能并不好, 例如, 针对SHA-256 采用Pinocchio3Pinocchio v0.5.3. https://github.com/amiller/pinocchio.中的电路生成器所生成的算术电路门数为58 160, 而根据SHA-256的算法可手动生成门数仅为27 904 的相应算术电路[89].
(2) 将C-SAT 问题转换为易证明的语言. 针对C-SAT 问题直接构造零知识证明往往无法实现简洁性, 一个构造零知识证明的平凡思路是在掩藏电路中每个导线值的同时完成验证计算, 而这会导致Θ(|C|) 级别的通信复杂度. 因此, 通常需将C-SAT 问题转换为易证明的语言(此步可能没有), 而易证明的语言在不同具体场景下也是不尽相同的. 例如, 在基于Linear-PCP 的零知识证明中, 需将C-SAT 问题转化为QAP 可满足问题, 即判断是否存在一个多项式能够被某个公开多项式整除; 在基于IPA 的零知识证明中, 需将C-SAT 问题中所有的线性约束和乘法门约束归约为判断一个多项式是否为零多项式的问题; 在基于DEIP 的零知识证明中, 需将C-SAT 问题转换为多元多项式的求和验证问题.
(3) 针对易证明的语言构造信息论安全证明. 许多简洁零知识证明都是基于信息论安全证明构造的,例如, 第一个简洁零知识论证[15]就是基于PCP 构造的; 基于MPC-in-the-Head 的零知识证明则是首先利用MPC-in-the-Head 构造零知识的PCP(或IPCP、IOP),然后调用合适的MPC 协议构造的; Bitansky 等人[58]和Setty 等人[62]也分别指出, 基于QAP 的零知识证明本质上是基于Linear-PCP 构造的. 具体的, 本文中出现的信息论安全证明包括PCP[16,17,59]、IPCP[64]、IOP[67,90]和Linear-PCP[58,62], 详见第4 章.
(4) 利用密码编译器将信息论安全证明转换为简洁非交互零知识证明. 密码编译器的作用包括:
• 实现谕示. 信息论安全证明需要理想谕示(Ideal Oracle), 而在实际的交互式证明中理想谕示是不存在的, 因此需借助承诺、哈希等密码工具实现. 由于这些密码工具大都是基于计算意义上的难题假设(如Pedersen 承诺的绑定性是基于DLOG 假设的), 因此证明也往往被削弱为论证.
• 实现非交互. 根据实现非交互所基于的模型, 分为基于CRS 模型和基于ROM 的零知识证明.例如, 基于QAP 的零知识证明均基于CRS 模型实现非交互, 而基于DEIP、IPA 和MPCin-the-Head 的零知识证明均基于ROM 实现非交互. 需要指出的是, 即使是基于ROM 实现非交互的零知识证明, 也可能需要公共参考串, 如ZKvSQL[51]、Libra[26]等.
• 实现零知识. 由于信息论安全证明本身可能不具备零知识性, 因此可能需利用密码编译器实现零知识性. 例如, 基于DEIP 和IPA 的零知识证明是通过承诺的隐藏性及盲化多项式实现的零知识性, 基于MPC-in-the-Head 的零知识证明是通过MPC 协议的隐私性实现的零知识性.
• 降低通信复杂度. 部分密码编译器有助于降低通信复杂度, 例如, 基于DEIP 的零知识证明可通过多项式承诺降低通信复杂度, 基于MPC-in-the-Head 的零知识证明可通过选取合适的底层MPC 协议降低通信复杂度.
3.2 简洁非交互零知识证明的性能评价标准
性能评价标准是衡量一个简洁非交互零知识证明协议优劣的准绳, 本部分从效率和安全性角度简要介绍简洁非交互零知识证明的性能评价标准, 见表3.

表3 简洁非交互零知识证明的性能评价标准Table 3 Performance evaluation of succinct NIZKAoK
在效率层面, 主要分为证明复杂度、验证复杂度、通信复杂度和是否需要公钥密码操作. 特别注意的是, 本文中的证明、通信和验证复杂度均为协议一轮的开销, 协议实际运行轮数及实际证明、验证计算开销和通信量与可靠性误差及安全级别有关.
(1) 证明复杂度: 证明复杂度是指在一轮协议中证明者生成证明所需计算步数的渐近复杂度. 在其他条件不变的情况下, 一个协议的证明复杂度越低, 协议的性能越好. 然而, 几乎所有的简洁非交互零知识证明协议都具有线性或准线性级别的证明复杂度, 仅从证明复杂度来看, 这些协议的差距并不大.
(2) 通信复杂度: 通信复杂度是指一轮协议证明规模的渐近复杂度. 在其他条件不变的情况下, 一个协议的通信复杂度越低, 协议的性能越好. 常见的亚线性通信复杂度为常数级别(zk-SNARK, 见第5 章)、根号级别(包括Ligero[35]、BooLigero[48])、对数级别(包括Aurora[50]等基于IOP 的零知识证明、Bulletproofs[31]等基于IPA 的零知识证明和Ligero++[36]等基于MPC-in-the-Head 的零知识证明). 特别的, 基于DEIP 的零知识证明只有满足电路深度与电路规模成对数关系时, 通信复杂度才是对数级别的.
(3) 验证复杂度: 验证复杂度是指一轮协议验证者验证证明有效性所需计算步数的渐近复杂度. 在其他条件不变的情况下, 一个协议的验证复杂度越低, 协议的性能越好. 需要指出的是, 一般而言由于验证者起码要读取整个陈述, 因此验证复杂度起码为线性. 但是, 可通过CRS 和预处理降低验证者参与协议后的计算开销. 例如DRZ20[54]就是利用CRS 中的结构化承诺密钥实现了对数级别的验证复杂度, Pinocchio 也可利用预处理实现常数级别配对操作的验证复杂度.
(4) 是否需要公钥密码操作: 对称密码操作是指移位、异或、域上多项式运算等对称密码中常出现的运算操作, 而公钥密码操作包括椭圆曲线上运算等公钥密码中常出现的运算操作. 一般而言, 公钥密码操作尤其是群幂运算的实际开销较高, 因此是否需要公钥密码操作会影响零知识证明协议的实际效率. 基于QAP 的零知识证明、基于DEIP 的零知识证明和基于IPA 的零知识证明均需要一定的公钥密码操作.
特别指出的是, 上述复杂度均与协议的安全参数成多项式关系. 因此, 即使是通信复杂度仅为常数个群元素的协议, 如Pinocchio[20], 其实际通信量也会随协议安全参数的改变而改变.
在安全性层面, 主要分为底层难题假设、系统参数生成方式和是否抗量子, 分别介绍如下.
(1) 底层难题假设: 不同简洁非交互零知识证明协议的底层难题假设通用性有一定的差距. 例如, 基于MPC-in-the-Head 的零知识证明所基于的假设是单向函数存在, 这是一种密码学中较为常见的假设. 第7 章中的零知识证明基于的难题假设是离散对数假设, 其相比于单向函数存在的假设通用性较低, 但也属于标准假设[24]. 第5 章中的零知识证明基于的假设是不可证伪假设, 其不属于标准假设. 底层难题假设的通用性是零知识证明落地应用的重要考量因素之一.
(2) 系统参数生成方式: 基于 CRS 的简洁非交互零知识证明 (如 Pinocchio[20]、Libra[26]和DRZ20[54]) 的系统参数必须由可信第三方生成, 这在去中心化的区块链应用中会带来安全性问题. 而一些基于ROM 实现非交互的简洁非交互零知识证明可利用某些哈希函数由证明者自行生成随机数, 在某种程度上具有更高的安全性.
(3) 是否抗量子: 基于MPC-in-the-Head 的零知识证明和部分基于IOP 的零知识证明(如Aurora)只需假设单向函数存在, 且仅有对称密钥操作, 被认为是抗量子的.
4 基于PCP、Linear-PCP、IPCP 和IOP 的零知识证明
1992 年, Kilian[15]基于概率可验证证明(PCP) 利用默克尔树和抗碰撞哈希函数构造了第一个简洁的交互式零知识论证, 后续的零知识证明大都是基于PCP 及其变种实现的. 值得一提的是, 虽然基于二次算术程序的简洁非交互零知识证明[19,91]似乎“摆脱了” PCP, 但这些协议本质是基于一种特殊的PCP,即Linear-PCP 实现的[58,62]. 除Linear-PCP 外, 基于其他对PCP 的扩展, 即IPCP 和IOP, 也可构造零知识证明. 本章第4.1 节介绍相关定义及概念, 第4.2 节分别介绍基于PCP、Linear-PCP、IPCP 和IOP 的零知识证明.
4.1 定义及概念
定义18(概率可验证证明[16,17,59]) 给定二元关系R, 概率可验证证明(probabilistically checkable proof, PCP) 指在证明者针对语言L(R) 生成证明谕示π后, 给定验证者访问请求谕示π任意位置比特的权限, 则验证者可通过生成最多r(λ) 长度的随机数进而访问请求谕示π的q(λ) 个比特值选择是否接受x ∈L(R). 该证明也具有完美完备性和可靠性(可靠性误差不多于1/2).
Arora 和Safra[17]指出, NP = PCP(logn,1), 即陈述长为n的NP 问题平凡证明与允许使用随机数长度为O(logn)、允许访问谕示数为O(1) 的PCP 等价.
定义19(线性PCP 与线性交互式证明[58]) 相比于PCP, 在线性PCP (linear-PCP) 中验证者V的访问请求q ∈Fm为行向量, 而证明者P的回答a ←πo·q为谕示和访问请求的内积.
线性交互式证明(linear interactive proof, LIP) 是指证明中证明者P仅能利用验证者V的消息进行线性/仿射运算的一类证明, 又由于V的消息蕴含在CRS 中, 故LIP 中证明πo与CRS 成线性/仿射关系.
利用Linear-PCP 可自然构造两轮LIP. 在LIP 中, 记Linear-PCP 中的证明谕示为πo,V的访问请求为(q1,q2,··· ,qk,qk+1), 且qk+1=α1q1+···+αkqk. 证明者返回{ai=πo·qi}i∈[k+1]. 由于限制了证明者只能计算qi的线性组合, 因此若V验证ak+1?=α1a1+···+αkak通过, 其会以较大概率相信P使用了一致的πo(可靠性误差不多于1/|F|).
定义20(交互式谕示证明[67,90]) 对于一个k(λ) 轮公开抛币的交互式谕示证明(interactive oracle proof, IOP), 在第i轮, 验证者V发送随机消息mi给证明者P, 随后P返回消息πi,k(λ) 轮交互结束后,P可构造证明谕示π=(π1,π2,··· ,πk). 随后V向π发起q(λ) 数目的访问请求并决定接受或拒绝.
在某种程度上, IOP 是IP 与PCP 的结合. 与IP 类似,k(λ) 轮IOP 也具有完备性和可靠性; 与PCP 类似, IOP 中也有描述谕示规模的参数和描述验证者访问请求次数的参数. 具体的, 记ri和rq分别为交互和访问请求的随机比特长度, 则对于x/∈L(R) 和恶意敌手P∗, 有
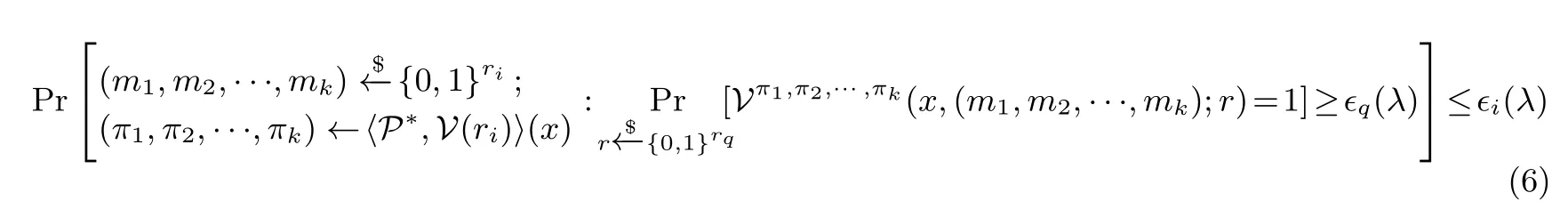
不等式(6) 的含义为随机性使得P∗以至少ϵq(λ) 大小概率欺骗成功的概率不超过ϵi(λ). 记IOP 的可靠性误差为ϵq(λ)+ϵi(λ), 则PCP 是ϵq(λ) = 0 的特殊IOP, IP 是ϵi(λ) = 0 的特殊IOP, 对NP 问题的平凡证明中ϵq(λ)=ϵi(λ)=0. 此外, IPCP 是k(λ)=1 的特殊IOP.
定义21(默尔克树[92]) 默尔克树(Merkle tree) 是一个二叉树, 其任意父节点的值等于左右子节点值连接后的哈希值. 记默克尔树根Root 为无父节点的节点, 叶子节点为无子节点的节点. 给定一组叶子节点值, 称该组叶子节点的节点路径为足以计算Root 所需的最少节点哈希值. 容易证明, 任意一组叶子节点的节点路径规模为O(logn), 其中n为叶子节点的个数.
4.2 典型协议分析
本节第4.2.1 小节介绍基于PCP 的零知识证明, 第4.2.2 小节介绍基于Linear-PCP 的零知识证明,第4.2.3 小节介绍基于IPCP 的零知识证明, 第4.2.4 小节介绍基于IOP 的零知识证明.
4.2.1 基于PCP 的零知识证明
Kilian92/Micali94. 1992 年, Kilian[15]基于PCP 利用默克尔树和CRHF 构造了简洁的交互式论证, 其思路如下. 首先验证者V和证明者P约定抗碰撞哈希函数H; 其次P生成PCP 的谕示证明π,并利用默克尔树对π承诺(哈希函数选用H), 将默克尔树根Root 发送给V; 然后V生成r(n) 个随机数发给P,P和V根据随机数、公共输入和Root 共同确定访问请求π的位置; 最后P揭示访问请求的位置值并将对应的节点路径哈希值发送给V,V计算Root 的值验证一致性并根据访问请求的位置值验证PCP 的正确性.
由于默克尔树的结构特点, 上述协议的通信复杂度可达到对数级别, 此外, 该协议的可靠性来自于哈希函数H的抗碰撞性. 值得一提的是, 上述协议本身不具备零知识性, 其零知识性是通过一种在不揭示承诺值的同时证明承诺值具有某种性质的方法实现的(notarized envelopes).
1994 年, Micali[18]利用ROM 下的Fiat-Shamir 启发式将上述协议修改为非交互. Valiant[93]进一步指出Micali 提出的方案是知识论证. 后续的工作通过引入PIR (private information retrieval)将Kilian92 中的四轮协议改进为两轮[94], 并利用抗碰撞可提取哈希函数(extractable CRHF) 替代了Micali94 中的ROM[70]. 近年, Chiesa 和Yogev 改进了Micali94 的通信复杂度[95], 并对其安全性进行了更为详细的探讨[96].
然而, 这些论证的实际性能均较差, 难以落地应用. 例如, 针对25×25 的矩阵乘法问题, 如果利用一个基于PCP 的经典零知识证明方案[97]构造协议, 那么该协议的实际证明和验证时间就已超过亿年[20].
ZKBoo/ZKB++/KKW18. ZKBoo[33]、ZKB++[34]和KKW18[47]的主要思路均是基于MPC-in-the-Head[98]的思想直接构造了高效零知识PCP, 随后将该零知识PCP 转换为NIZKAoK.其核心思路是证明者在脑海中模拟一个安全多方计算协议的运行并生成MPC 参与方数目的视图, 然后验证者随机挑选若干视图验证正确性和一致性,协议的零知识性由安全多方计算协议的隐私性保障. 从PCP的角度, 证明者生成的视图就是谕示, 验证者挑选的视图就是访问请求. 本文第8.3.1 小节介绍ZKBoo 和ZKB++, 第8.3.2 小节介绍KKW18.
4.2.2 基于Linear-PCP 的零知识证明
Bitansky 等人[58]指出,zk-SNARK(包括GGPR13[19]、Pinocchio[20]、Groth16[52]、GKMMM18[41]等) 均是基于Linear-PCP 实现的. 其步骤为首先将Linear-PCP 转换为LIP, 再将LIP 转换为SNARK,最后将SNARK 转换为zk-SNARK. 首先, 将Linear-PCP 转换为LIP 是自然的, 见定义19. 其次, 利用一种特殊的密码编码方法(可基于KEA 假设实现, 其需具有单向性、允许公开验证二次等式、保障证明者只能进行线性运算, 详见第5.2.2 小节), 任意LIP 都可转换为特定验证者的SNARK, 具有低度验证者(low-degree verifier) 的LIP 可转换为公开可验证的SNARK. 然后, 通过随机化处理, SNARK 可转换为zk-SNARK. 此外, Bitansky 等人给出了将若干具体PCP[59,99,100]转换为Linear-PCP 的方法. 基于Bitansky 等人构造zk-SNARK 的思路, Ben-Sasson 等人[81]及Groth[52]通过构造高效的Linear-PCP 和LIP 优化了zk-SNARK 的理论和实际性能. 本文第5.3.1 小节介绍Pinocchio, 第5.3.2 小节介绍Groth16, 第5.3.3 小节介绍GKMMM18.
4.2.3 基于IPCP 的零知识证明
Ligero. Ligero 系列协议[35,36,48]均是基于IPCP 的零知识证明, 其也是利用MPC-in-the-Head的思想直接构造了零知识的IPCP. 与基于PCP 的零知识证明不同, 基于IPCP 的零知识证明允许证明者生成谕示后根据验证者的随机挑战构造新谕示并进一步完成证明. 具体的, 在Ligero 系列协议中, 证明者首先利用RS 码将证据编码为一个m×n的矩阵, 然后根据验证者的随机挑战r ∈Fn计算矩阵行与r的线性组合返回给验证者, 验证者通过该线性组合验证协议的正确性, 协议的可靠性由RS 码保障,零知识性由RS 码和随机掩藏多项式保障. 本文第8.3.3 小节介绍Ligero 和Ligero++, 第8.3.4 小节介绍BooLigero.
4.2.4 基于IOP 的零知识证明
Ben-Sasson、Chiesa 和Spooner[90]指出, 在ROM 下IOP 可以被转换为非交互论证, 并可利用已有的零知识编译方法, 构造系统参数可公开生成的简洁NIZKAoK. 同基于PCP 的零知识证明类似, 基于IOP 的零知识证明也具有仅需对称密钥操作、可抗量子的优点; 不同的是, 基于IOP 的零知识证明具有更好的性能[66,101]. 基于不同底层关键技术构造IOP, 如sum-check 协议、RS 码、MPC-in-the-Head 等可构造性能不同的简洁NIZKAoK, 分列如下.
基于DEIP 的零知识证明. Sum-check 协议[63]可用于证明某函数的遍历求和值等于公开值(具体见定义30). Sum-check 协议本质上属于IOP, 其中P的证明谕示为g(x1,x2,··· ,xℓ),V的访问请求次数为1, 即g(r1,r2,··· ,rℓ). 基于sum-check 协议, Goldwasser、Kalai 和Rothblum[61]提出了一个针对分层算术电路求值问题的交互式证明, 该协议由于证明和验证复杂度均较低, 故被称为双向高效的交互式证明(doubly efficient interactive proof, DEIP). 后续的研究如文献[26–29,32,51] 利用Cramer 和Damgård 的转换方法[102]将DEIP 转换为简洁零知识知识论证, 并利用Fiat-Shamir 启发式转换为简洁NIZKAoK. 该类零知识证明的主要思路、构造方法、性能表现和典型协议详见第6 章.
Aurora. Aurora 由Ben-Sasson 等人[50]提出, 他们构造了针对R1CS 可满足问题的IOP, 并利用已有的零知识编译方法[101], 实现了证明复杂度为O(nlogn)、通信复杂度为O(logn)、验证复杂度为O(n) 的简洁NIZKAoK, 其中n为R1CS 可满足问题的规模. Aurora 的主要思路如下.
首先将R1CS 可满足问题转换为两种检查, 即列检查和行检查. 其中, 列检查为给定向量a,b,c ∈Fm×1, 检查a ⊙b?=c; 行检查为给定向量a,b ∈Fm×1及矩阵M ∈Fm×m, 检查Mab. 显然, R1CS可满足问题是可满足的当且仅当对yA=Az,yB=Bz,yC=Cz的行检查成立和对yA ⊙yB=yC的列检查成立.
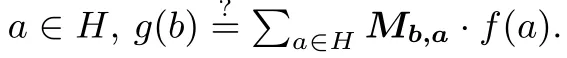
接着, 对于列检查, Aurora 援引Ben-Sasson 和Sudan 的标准概率检查方法[103]构造了对应的IOP,其主要思路如下. 对于任意的a ∈H,f(a)g(a)−h(a) = 0 等价于存在p(x), 使得f(x)g(x)−h(x) =p(x)ZH(x), 其中ZH(x) 是度为|H| 且在集合H上均为0 的唯一多项式, 则列检查可等价转换为对多项式p(x) 的低度检查问题, 即检查码p ∈RS[L,2ρ −|H|/|L|]. 对于行检查, 注意到其问题形式为求和, 故可利用sum-check 协议; 然而与一般sum-check 协议不同的是, 行检查的求和函数不是多变量而是单变量,sum-check 协议的核心思路是每轮将多变量求和函数转换为单变量函数, 针对单变量求和函数直接调用sum-check 协议是困难的. 基于此, Aurora 指出当集合H是F 的陪集时, 可构造单变量求和验证协议, 并利用该协议构造通信复杂度为O(logd) 的IOP, 其中d为求和函数的度. 最后, Aurora 利用Ben-Sasson等人的零知识编译方法[101]实现了上述IOP 的零知识并最终构造了简洁NIZKAoK.
Stark. Stark 由Ben-Sasson 等人[43]提出, 是一种针对可用对数空间可计算电路表示的陈述的非交互零知识论证, 比如随机存取机(random access machine) 上的有界停机问题(bounded halting problem). 给定一个程序P和时间上界T(n), 若其可用空间大小为O(logT(n)) 的电路表示, 则Stark可以证明“P可在T步内接受”, 且生成证明的时间为O(TlogT), 证明的长度为O(logT), 验证时间为O(|P|+poly logT), 这相比于平凡验证时间Ω(|P|+T) 有显著优化.
同Aurora 相比, Stark 仅支持均匀计算(uniform computation) 问题, 而Aurora 可支持非均匀计算问题(如非均匀电路). 事实上,O(|C|) 规模的C-SAT 问题也可转换为{|P|,T=Ω(|C|)}的有界停机问题. 此时, Stark 的证明复杂度为O(|C|log2|C|), 通信复杂度为O(log|C|), 验证复杂度为O(|C|). 由于Stark 不能直接针对C-SAT 问题, 本文不再详述.
Limbo. Limbo 由Guilhem、Orsini 和Tanguy[49]提出, 其拓展了Ligero 中的MPC 模型并基于IOP 实现, 是一种虽然通信复杂度与电路规模成线性关系, 但是实际性能良好的NIZKAoK. 对于算术电路, 相比于文献[33–36], Limbo 实现了针对中等规模C-SAT 问题(乘法门少于500 000 个) 的最优实际性能. 具体的, Limbo 给出了一个较为适合MPC-in-the-Head 的MPC 模型, 即客户-服务器模型(client-server model), 然后基于该模型和IOP 实现了乘法门约束的高效验证进而构造了简洁NIZKAoK.本文第8.3.5 小节介绍Limbo.
4.3 本章小结
本章简要介绍了基于PCP、IPCP、Linear-PCP 和IOP 的零知识证明, 简单给出了若干典型协议的主要思路和底层关键技术, 并指出了这些简洁非交互零知识证明的构造方法——首先构建信息论安全证明, 然后利用密码编译器将信息论安全证明转换为简洁非交互零知识证明. 本书第5–8 章将以底层关键技术为线索, 较为详细地介绍目前较为主流的几种简洁非交互零知识证明.
5 基于QAP 的零知识证明
本章介绍基于二次算术程序(QAP) 的零知识证明. 该类零知识证明又被称为zk-SNARK, 其均基于CRS 模型实现非交互. 从信息论安全证明的角度, zk-SNARK 是基于Linear-PCP[58,62]及LIP[58]实现的; 从密码编译器应用的底层关键技术角度, 其大多利用QAP[19]将C-SAT 问题归约为一组多项式的约束并利用双线性配对验证上述约束进而实现. 虽然早期的zk-SNARK[91,104]并不是基于QAP 实现的,并且Bitansky 等人[70]指出利用知识可提取假设就足以构造zk-SNARK, 但是不论是在理论还是实际应用层面, 大部分zk-SNARK 均是基于QAP 及其变种[19,20,22,105–110]实现的, 故本文将该类零知识证明称为基于QAP 的零知识证明.
zk-SNARK 协议较多, 且Nitulescu[55]对zk-SNARK 已有较为详细的介绍, 本文仅介绍若干典型协议,其性能表现、底层难题假设、关键技术等列于表4,zk-SNARK 的其他协议及具体细节可参考文献[55].

表4 部分zk-SNARK 总结Table 4 Summary of several zk-SNARK
5.1 定义及概念
定义22(SNARG 与SNARK[25,58,81]) SNARG 是算法三元组∏=(Setup,Prove,Verify). 给定一个多项式时间内可判定的二元关系R及其对应的NP 语言L(R), 启动算法(σ,τ)←Setup(1λ,R) 以安全参数λ的一元表示和关系R为输入,生成参考串σ和模拟陷门τ. 证明生成算法π ←Prove(R,σ,x,w)用于生成证明π. 验证算法0/1←Verify(R,σ,x,π) 用于验证证明.
称三元组算法(Setup,Prove,Verify) 为公开可信预处理SNARG (publicly verifiable preprocessing succinct non-interactive argument, SNARG) 当如下条件满足.
• 完备性. 对于任意的x ∈L(R), 若算法Setup 和Prove 正确运行, 则验证者V一定会接受.
• 可靠性. 对于任意PPT 的P∗, 任意的x/∈L(R),P∗能使V接受的概率不超过negl(λ).
• 高效性. Setup 的运行时间为poly(λ+|x|), Prove 的运行时间为poly(λ+|x|), Verify 的运行时间为poly(λ+|x|).
• 简洁性. 证明者发送的消息规模不超过poly(λ)(|x|+|w|)o(1).
如果Setup 的运行时间为poly(λ+log|x|), 则称一个SNARG 为完全简洁的(fully succinct)[111].SNARK (succinct non-interactive argument of knowledge) 是指具有(计算意义) 的知识可靠性的SNARG, zk-SNARK 是指具有零知识性的SNARK. 其中, (计算意义) 的知识可靠性是指如果敌手能够生成一个针对某语言的有效证据, 那么就存在一个多项式的提取器可将这个有效证据提取出来, 且该提取器能够访问敌手的任意状态. 具体而言, 知识可靠性是指对于任意的多项式敌手A, 都存在一个多项式时间的提取器XA, 使得下式成立
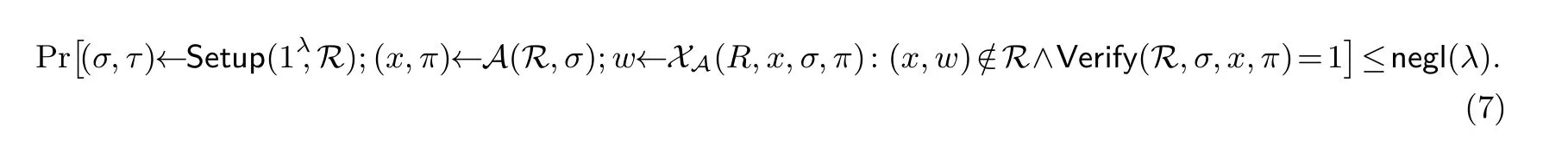
定义23(二次算术程序[19]) 二次算术程序(quadratic arithmetic program, QAP) 是二次张成程序(quadratic span program,QSP)[19]在算术电路上的自然扩展,而后者是对张成程序(span program)[112]的扩展. 域F 上的QAPQ= (t(z),U,W,У) 包含三组多项式U={uk(z)},W={wk(z)},У={yk(z)}(k ∈0∪[m]) 和目标多项式t(z). 记公共输入为(c1,c2,··· ,cN), 则称Q是可满足的当且仅当存在系数(cN+1,cN+2,··· ,cm) 使得t(z) 整除p(z), 其中

即存在多项式h(z) 使得p(z)−h(z)t(z)=0. 称Q的规模为m,Q的度为t(z) 的度, 即d.
强QAP(strong QAP)[19]是指对于任意一组(a1,a2,··· ,am,b1,b2,··· ,bm,c1,c2,··· ,cm), 如果其构成的p(z) 可被t(z) 整除, 则有(a1,a2,··· ,am)=(b1,b2,··· ,bm)=(c1,c2,··· ,cm), 其中
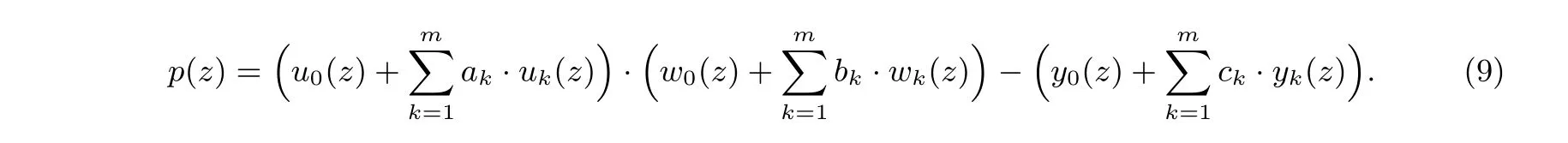
自然的, QAP 可视为3 组Linear-PCP, 每组访问请求次数为1.

5.2 背景及主要思路
5.2.1 背景
2006 年, Groth、Ostrovsky 和Sahai[115]利用双线性配对构造了第一个基于标准假设且通信复杂度为线性的非交互零知识证明. 2010 年, Groth[91]基于CRS 模型、q-PKE 假设和q-PDH 假设, 利用双线性配对实现了第一个不需依赖ROM 且通信量为42 个群元素的zk-SNARK. Groth 的核心思路是将C-SAT 问题归约为一组等式并利用双线性配对验证等式成立, 然而该协议的CRS 规模和证明复杂度均为O(|C|2). Lipmaa[104]将上述协议的CRS 规模降低到了O(|C|log|C|), 但证明复杂度仍为O(|C|2).
2013 年, Gennaro 等人[19]提出了QAP, 其是一种新的NP 语言且利用QAP 可将算术电路可满足问题快速归约为QAP 可满足问题, 即判断是否存在一个多项式能够被某个公开确定多项式整除的问题.Gennaro 等人利用强QAP 构造了CRS 规模为O(|C|)、证明复杂度为O(|C|log|C|)、通信量为9 个群元素的zk-SNARK (记作GGPR13). 同年, Parno 等人[20]提出了Pinocchio, 在将通信量进一步降低到了8 个群元素的同时弱化了GGPR13 对QAP 的限制, 即利用一般QAP 构造了zk-SNARK, 这将GGPR13 中的CRS 规模降低了约2/3, 同时也降低了预处理时间和证明者计算开销. Pinocchio 具有良好的实际性能, 在一定程度上促使了零知识证明的落地应用. Zcash[7]就是基于该类零知识证明[22]所构造的一种隐私密码货币, 能够在防止双花的同时实现交易的匿名性. 在Pinocchio 之后, 一系列研究着力于优化该类零知识证明的实际性能[22,107–109]并应用于不同场景中, 例如对认证数据的隐私保护证明[108]、大数据计算[116,117]和可验证计算中. 特别的, 对于可验证计算, 其思路主要是先将C 语言程序转换为某种编程语言(例如具有固定内存访问和控制流的C 语言程序[20]、RISC[22,81]、RAM[65,116]等), 再将中间语言转换为电路并调用针对电路可满足问题的零知识证明完成计算; 也有直接构造针对算术电路变种(如集合电路[107]) 的零知识证明从而完成可验证计算的.
除了改进zk-SNARK 的性能之外, 还有系列研究探讨了zk-SNARK 的特征和性质. Gentry 和Wichs[25]指出基于黑盒归约和可证伪假设无法构造SNARG. Bitansky 等人[70]指出构造zk-SNARK必须依赖于可提取抗碰撞哈希函数, 同时文献[111] 指出基于PCD 系统(proof-carrying data system),任何zk-SNARK 都可高效转换为完全简洁的zk-SNARK. Groth[52]基于非对称双线性映射构造了通信量仅为3 个群元素、验证者计算开销为3 个配对运算的zk-SNARK. 此外, Groth 还指出基于通用非对称双线性群模型(general asymmetric bilinear group model)[118]无法构造通信复杂度为1 个群元素的zk-SNARK.
Linear-PCP. Bitansky 等人[58]指出, zk-SNARK 均是基于Linear-PCP 实现的, 其步骤如下. 首先将线性概率可验证证明转换为线性交互式证明, 该转换是自然的, 见定义19; 再将线性交互式证明转换为SNARK, 利用一种特殊的密码编码方法(可基于指数知识假设假设实现, 其需具有单向性、允许公开验证二次等式、保障证明者只能进行线性运算, 详见第5.2.2 小节), 任意LIP 都可转换为特定验证者的SNARK, 具有低度验证者(low-degree verifier) 的LIP 可转换为公开可验证的SNARK; 最后通过引入随机化处理, 可将SNARK 转换为zk-SNARK. 此外, Bitansky 等人也给出了将若干具体PCP[59,99,100]转换为Linear-PCP 的方法. Bitansky 等人提供了一种构造zk-SNARK 的新思路. 基于该种思路, Ben-Sasson 等人[81]及Groth[52]通过构造高效Linear-PCP 和LIP 优化了zk-SNARK 的理论和实际性能.
可更新的零知识证明. 上述zk-SNARK 存在两个问题, 第一个问题是协议需要安全生成的公共参考串, 若公共参考串中含有的秘密信息被攻击者获知, 则整个协议就不再具备可靠性. 启动阶段的私密性和区块链的去中心化产生了较为严重的矛盾, 在一定程度上影响了zk-SNARK 的进一步应用. 为解决该问题, Ben-Sasson 等人[79]和Bowe、Gabizon 及Green[80]指出可以利用安全多方计算生成公共参考串,但如何选择参与方及如何保障安全性是一个新的难题. 第二个问题是公共参考串与陈述是相关的, 即待证明陈述改变后需重新进行预处理, 然而预处理阶段的复杂度为O(|C|2log2|C|), 多次预处理会严重影响协议性能.
针对上述问题, Groth 等人[41]基于QAP 提出了一种CRS 全局且可更新(updatable universal CRS)的zk-SNARK(记作GKMMM18). 可更新是指对CRS 安全性持怀疑态度的用户可以发起对CRS的更新请求, 只要旧CRS 和更新发起者中有一个是诚实的, 新CRS 就是安全的. 全局是指根据一个全局公共参考串可以生成多个针对具体电路的公共参考串, 其中全局公共参考串与待证明陈述独立, 可预先生成; 针对具体电路的公共参考串与陈述相关, 给定陈述后才能生成. GKMMM18 可根据O(|CM|2) 级别的全局CRS 生成O(|CM|) 级别的陈述相关CRS. 此外, Groth 等人还指出CRS 中仅含单项式的zk-SNARK 易实现可更新, 而CRS 中含有非单项式的zk-SNARK 难以实现, 他们还证明了Pinocchio 无法实现可更新.
GKMMM18 虽然实现了全局可更新的CRS, 但一方面根据全局CRS 构造陈述相关CRS 需进行额外预处理, 另一方面更新CRS 需要平方级别的群幂运算. 在此基础上, Maller 等人[40]提出的Sonic 通过置换论证(permutation argument)、大积论证(grand-product argument)等技术在代数群模型(algebraic group model)[119]下实现了CRS 全局可更新的、规模为O(|C|)、不需额外预处理的简洁NIZKAoK. 后续的工作,如Plonk[23]、Marlin[42]和AuroraLight[120],改进了Sonic 的实际性能,但也是基于代数群模型或知识假设实现的. 2020 年, Daza、Rafols 和Zacharakis[54]基于离散对数假设(见第7.1 节) 通过结构化承诺密钥改进了内积论证从而实现了CRS 可更新的简洁NIZKAoK (记作DRZ20). 值得注意的是,在这些可更新的零知识证明中, 只有GKMMM18 是基于QAP 的, 本文第5.3.3 小节介绍GKMMM18,第7.3.3 小节介绍DRZ20.
5.2.2 主要思路
本小节以Pinocchio[20]为例, 介绍zk-SNARK 的构造思路. 首先介绍如何将C-SAT 问题归约为QAP 可满足问题, 然后介绍如何利用“掩藏” 编码和双线性配对实现针对QAP 可满足问题的zk-SNARK.

为了更好地理解“有贡献” 的概念, 本小节在图3 中给出一个例子. 对门r6的左输入“有贡献” 的是导线c1和c2, 故u1(r6) =u2(r6) = 1; 对门r5的左输入“有贡献” 的是导线c3, 故u3(r5) = 1.wi(rg)和yi(rg) 同理, 其分别考虑的是对门右输入和输出的贡献, 且度至少为d −1.

图3 算术电路可满足问题与QAP 可满足问题的归约[19,20]Figure 3 Reduction from arithmetic C-SAT problem to QAP satisfiability problem
除QAP 外, 还可将C-SAT 问题归约为其他形式的可满足问题, 针对不同形式的具体问题, 其归约过程更为高效. 如针对布尔电路的QSP[19]、利用纠错码构造的高效QSP[105]及SSP (square span programs)[106]和针对算术电路的SAP (square arithmetic programs)[110]. 这些可满足问题的形式与QAP 可满足问题的形式类似, 且基于其构造zk-SNARK 的思路也是类似的, 本文只详细介绍QAP.
针对QAP 可满足问题构造zk-SNARK 的主要思路. 针对QAP 可满足问题构造zk-SNARK 的主要思路列于图4. 直接证明多项式p(z) 可被t(z) 整除可能是困难的, 而这可等价转换为证明者证明其拥有p(z) 和h(z), 且p(z) =h(z)t(z). 由于u(z)、w(z)、y(z) 和t(z) 可由验证者根据电路结构自行计算, 因此证明者可发送(cN+1,cN+2,··· ,cm) 及h(z). 然而, 考虑到h(z) 的度约为d, 直接发送h(z)将导致O(|CM|) 级别的通信复杂度. 利用Schwartz-Zippel 引理可将传输多项式简化为传输多项式在某点的取值进而降低通信复杂度, 即验证者V挑选随机挑战s$←−F, 随后P返回p(s) 和h(s),V验证p(s)−h(s)t(s)0.
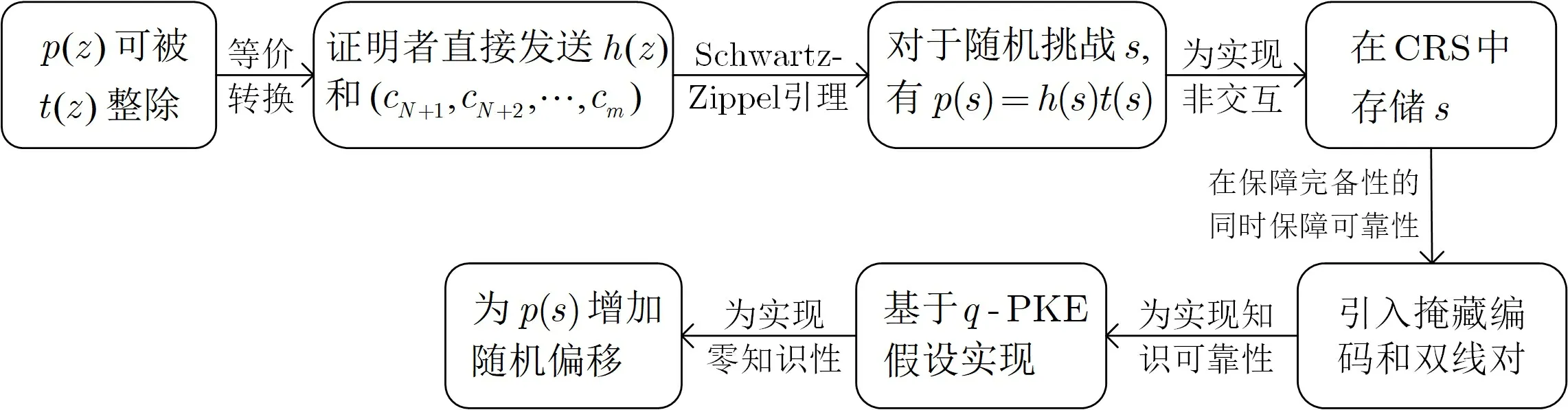
图4 针对QAP 可满足问题构造zk-SNARK 的主要思路[19,20]Figure 4 Main idea of constructing zk-SNARK for QAP satisfiability problem
然而, 上述方法既需要交互, 又不能保障恶意证明者在获知s后无法伪造p(s) 和h(s). 前者可通过CRS 解决, 但在CRS 中直接存储s仍无法解决后者, 因此需引入某种编码方式“掩藏”s. 需要注意的是, 若记该“掩藏” 方式为Enc, 则Enc 至少需具备四个特点, 一是Enc(s) 具有一定的单向性, 获取Enc(s) 难以推知s; 二是为了实现公开可验证的zk-SNARK, CRS 中不能存储秘密而只能存储公共信息, 如Enc(1),Enc(s),··· ,Enc(sd−1); 三是利用Enc(1),Enc(s),··· ,Enc(sd−1) 可构造多项式Enc(h(s)),Enc(p(s)),Enc(t(s)), 即Enc 支持线性运算; 四是Enc 需支持二次等式的验证, 该运算用于验证Enc(p(s)−h(s)t(s))Enc(0). 事实上, 给定素数阶p的循环群G,GT, 若有双线性映射e:G×G→GT且对于任意的a,b ∈Zp有e(ga,gb)=e(g,g)ab, 则Enc(a)=ga即可满足上述要求.
上述方法仍存在几个问题. 一是无法保障知识可靠性, 即无法保障证明者确实利用了 (cN+1,cN+2,··· ,cm) 构造Enc(p(s)), 而知识可靠性可基于q-PKE 假设得以保障; 二是可能无法保障零知识性, 验证者虽难以通过Enc(p(s)) 和Enc(h(s)) 直接推知私密信息, 但仍可能获知某些隐私信息, 这可通过随机化处理p(s) 从而实现统计意义的零知识性.
基于以上思路可构造通信复杂度为常数个群元素的零知识证明, 具体见第5.3 节.
5.3 典型协议分析
本节介绍基于QAP 的零知识证明典型协议(见图5), 分析各协议的构造思路、协议流程、复杂度及安全性. 本节第5.3.1 小节介绍Pinocchio, 第5.3.2 小节介绍Groth16, 第5.3.3 小节介绍GKMMM18.

图5 基于QAP 的部分零知识证明协议优化思路Figure 5 Optimization of several zero-knowledge proof based on QAP
5.3.1 Pinocchio
Pinocchio 由Parno 等人[20]提出, 其通信复杂度为8 个群元素, 且验证复杂度仅与输入输出成线性关系. 本小节简要介绍Pinocchio 的主要思路、协议流程(见协议1) 和复杂度及安全性.


协议1 Pinocchio [20]公共输入: 域F, 算术电路C : F|x|+|w| →F|y|. 其中(x,y) = (c1,c2,··· ,cN), |x|+|y| = N.证明者秘密输入: w = (cN+1,cN+2,··· ,cm), 记集合Imid = {N +1,N +2,··· ,m}.1. 可信初始化阶段.(1) 由可信第三方将算术电路C 的可满足性问题归约为QAP 可满足问题, 构造对应QAP 串(t(z),U,W,У),其规模为m, 度为d.(2) 由可信第三方生成相应参数. 生成生成元为g 的群G 及双线性映射群GT. 选取随机数ru,rw,ry,s,αu,αw,αy,β,γ$←−F 并令ry ←rurw,gu ←gru,gw ←grw,gy ←gry.(3) 由可信第三方生成公共参考字符串. 证明者P 的参考串为{guk(s)}{}{}u ,gwk(s)w ,gyk(s)y ,{k∈Imid k∈Imid k∈Imid gαuuk(s)}{}{}u gαwuk(s)k∈Imid,w gαyuk(s)y{gsi}{k∈Imid,}k∈Imid,i∈0∪[d−2],gβuk(s)ugβwk(s)wgβyk(s)y k∈Imid,u,gαwt(s)w,gαyt(s)y,gβt(s)u,gβt(s)w,gβt(s)y.验证者V 的参考串为gαut(s)()g,gαu,gαw,gαy,gγ,gβγ,gt(s)y ,{guk(s)u,gwk(s)w,gyk(s)y}k∈0∪[N].2. 证明者P 生成证明. P 首先选取δu,δw,δy$←−F, 然后他利用证据w 构造p(z) 并计算p′(z) ←(u0(z)+uio(z)+umid(z)+δut(z))·(w0(z)+wio(z)+wmid(z)+δwt(z))−(y0(z)+yio(z)+ymid(z)+δyt(z)),h′(z) ←p′(z)/t(z),其中, umid(z) = ∑k∈Imid ck ·uk(z), wmid(z) 和ymid(z) 同理. P 利用参考串生成证明π(gu′mid(s)u,gw′mid(s)w,gy′mid(s)y,gαuu′mid(s)u,gαww′mid(s)w,gαyy′mid(s)y,gh′(s),gβu′mid(s)ugβw′mid(s)wgβy′mid(s)y),}其中, u′mid(s) = umid(s)+δut(s), 可根据{mid(s),y′mid(s) 同理. 记h′(z) = ∑d−2 guk(s)u k∈Imid计算得出, w′i=0 h′izi, 则gh′(s) 可由∏di=1(gsi)h′i 计算得出.3. 验证者V 验证证明. 记V 收到的证明为π = (gUmid,gWmid,gYmid,gˆUmid,gˆWmid,gˆYmid,gH,gZ), 则V 进行如下三项检查.(1) V 检查P 可以构造Umid, 即P 拥有Umid 的系数. Wmid,Ymid 同理. 具体的, V 检查e(gˆUmid(((((u,g) ?=e gUmid u,gαu),e gˆWmid w,g) ?=e gWmid w,gαw),e gˆYmid y,g) ?=e gYmid y,gαy).(2) V 检查t(s) 可以整除p(s). 具体的, V 先计算guio(s)u←∏(k∈[N]guk(s)u)ck, gwio(s)w,gyio(s)y同理.V 随后验证e(gu0(s)uguio(s)ugUmidu,gw0(s)wgwio(s)wgWmidw) ?= e(gt(s)y ,gH)()e gy0(s)ygyio(s)ygYmidy,g .(3) V 检查Umid,Wmid,Ymid 是由同一组系数生成的. 具体的, V 检查e(gZ,gγ) ?= e(gUmid ugWmidwgYmidy,gβγ).输出: 比特b, 当且仅当上述三项检查均通过, 输出b = 1; 否则输出b = 0.

协议流程. Pinocchio 的协议流程如协议1 所示. 在可信初始化阶段, 由可信第三方将C-SAT 问题归约为QAP 可满足问题, 并生成证明者和验证者的公共参考串. 在生成证明阶段, 证明者利用证据w生成证明π, 其规模为8 个群元素. 在验证证明阶段, 验证者共需验证五个配对等式, 其中第一项检查用于验证证明者确实拥有Umid(s)、Wmid(s) 和Ymid(s) 的系数; 第二项检查用于验证t(s) 可以整除p(s); 第三项检查用于验证Umid、Wmid和Ymid是由同一组系数生成的.
讨论总结. 现简要分析Pinocchio 可被视为基于Linear-PCP 构造的原因. 首先, 可以认为谕示证明是

因此可被视为是一种PCP. 另外, 显然证明π与证明者的参考串存在线性关系, 因此Pinocchio 可被视为基于Linear-PCP 构造.
接着分析Pinocchio 的复杂度和安全性. 首先分析复杂度. 在预处理阶段, 将算术电路可满足问题归约为QAP 可满足问题, 其主要开销为根据点值构造度为d的共3m个多项式, 若利用FFT 计算拉格朗日插值[121], 该阶段的计算开销为O(mdlog2d) 接着分析安全性. 基于d-PKE、q-PDH 和2q-SDH 假设,Pinocchio 可被证明是知识可靠的[20]. 其中d-PKE 假设可保障证明者P拥有证据w=(cN+1,cN+2,··· ,cm) (协议1 第3 步的(1)),q-PDH 假设和2q-SDH 假设可保障知识可靠性. 对于零知识性, Pinocchio 通过随机化处理umid(z), 即引入δut(z)(wmid(z),ymid(z) 同理) 从而实现了统计意义的零知识性. 5.3.2 Groth16 在限定敌手只能进行线性/仿射运算的情况下, Groth[52]基于QAP 构造了通信量仅为3 个元素的LIP, 并基于该LIP 构造了通信量为3 个群元素、验证者计算开销仅为4 个配对运算的zk-SNARK (记为Groth16). 现介绍Groth16 的主要思路、协议流程并分析复杂度和安全性. 主要思路. Bitansky 等人[58]指出zk-SNARK 均可视为基于Linear-PCP 和LIP 实现的, 在此基础上Groth 给出了一个更为详细的LIP 定义. 给定形式如下的算法三元组(Setup,Prove,Verify), 如果其具有完美完备性和统计意义的知识可靠性(对于只能进行线性/仿射运算的敌手), 则称该算法组是LIP. • (σ,τ)←Setup(1λ,R). 参数生成算法以安全参数λ的一元表示和NP 关系R为输入, 生成参考串σ和模拟陷门τ. •π ←Prove(R,σ,x,w). 证明生成算法分为两步, 首先运行Π←ProofMatrix(R,x,w) 生成矩阵Π, 其中ProofMatrix 为PPT 的矩阵生成算法, 然后计算证明π ←Πσ. • 0/1←Verify(R,σ,x,π). 验证算法分为两步, 首先运行确定性多项式算法Test(R,x) 生成函数t(·)←Test(R,x), 然后验证者检查t(σ,π)?=0, 当且仅当其为0 时接受, 否则拒绝. 在此基础上, 如果LIP 具有完美零知识性, 则可利用其构造zk-SNARK. 其中, 完美零知识性是指存在PPT 算法Sim, 使得对于任意的R及(x,w)∈R, 对于任意的敌手A, 都有 协议流程Groth16 的协议流程如协议2 所示, 其与对应的零知识LIP 的区别仅在于前者引入了双线性配对用于验证t(σ,π)?=0 (即协议2 第3 步V检查). 讨论总结. 首先分析安全性. 上述论证可以证明具有完美完备性和完美零知识性, 在敌手只能进行线性/仿射运算的情况下, 该论证可被证明是统计意义知识可靠的. 完美完备性来源于零知识LIP. 由于r1,r2的随机性, 真实证明中的A、B和模拟器生成的A、B是分布一致的, 又C由A、B确定, 因此完美零知识性得以保障. 现简要分析知识可靠性. 考虑不加随机数r1,r2的版本, 对于只能进行线性/仿射运算的敌手, 其伪造证据A′的形式为 其次分析复杂度. Groth16 的参考串包含(m+2d+2) 个G1群中的元素和(d+3) 个G2群中的元素. 证明者计算开销主要为计算证明π, 具体为O(|C|) 次群上运算. 通信复杂度为2 个G1群中的元素和1 个G2群中的元素. 验证者计算开销为4 次配对运算. 协议2 Groth16 [52]公共输入: 域F, 算术电路C : F|x|+|w| →F|y|. 其中(x,y) = (c1,c2,··· ,cN), |x|+|y| = N.证明者秘密输入: w = (cN+1,cN+2,··· ,cm), 记集合Imid = {N +1,N +2,··· ,m}, 显然有|w| = |Imid|.1. 可信初始化阶段.(1) 由可信第三方将算术电路C 的可满足性问题归约为QAP 可满足问题. 根据电路C 构造对应的QAP 串(t(z),U,W,У), 其规模为m, 度为d.(2) 由可信第三方生成相应参数. 生成生成元为g、h 的群G1、G2 及双线性映射群GT. 映射e 定义为e : G1 ×G2 →GT. 记[a]1 为ga, [b]2 为hb, [c]T 为e(g,h)c. 选取随机数α,β,γ,δ,s$←−F.(3) 由可信第三方生成公共参考字符串σ = ([σ1]1,[σ2]2) 和模拟陷门τ = (α,β,δ,γ,s). 其中{βui(s)+αwi(s)+yi(s)}N■■■α,β,δ,{si}d−1 i=0 ,{σ1 ={βui(s)+αwi(s)+yi(s)}m γ{sit(s)}d−2 i=0■■■,σ2 = (β,γ,δ,δ i=N+1,δ si}d−1 i=0).i=0 2. 证明者P 生成证明. P 随机挑选r1,r2$←−F 并计算证明π = ([A]1,[C]1,[B]2), 其中A = α+m∑ciui(s)+r1δ,B = β +m∑ciwi(s)+r2δ,i=0 i=0+Ar2 +Br1 −r1r2δ.3. 验证者V 验证证明. V 检查e([A]1,[B]2)?= e([α]1,[β]2)e C =∑m i=N+1 ci(βui(s)+αwi(s)+yi(s))+h(s)t(s)δ( N∑ci[βui(s)+αwi(s)+yi(s))]1,[γ]2 e([C]1,[δ]2).i=0 γ输出: 比特b, 当且仅当上述检查通过, 输出b = 1; 否则输出b = 0. 5.3.3 GKMMM18 然而, 针对包含多项式的CRS 实现可更新性是困难的. 考虑对gf(s)的更新, 若随机选取δ并将旧CRS 更新为gf(s)δ, Groth 等人证明了任意可完成上述更新的敌手都可提取出单项式(g,gsδ,··· ,gsnδ),依据这些单项式, 敌手可破坏Pinocchio 等zk-SNARK 的知识可靠性. 针对上述问题, Groth 等人采用了一种与 Pinocchio 及 Groth16 不同的证明方法. 考虑一个QAPQ= (t(z),U,W,У), 由于CRS 中不能包含多项式, 因此无法继续使用之前基于QAP 的方法, 即通过随机挑选s构造与QAP 对应的多项式编码进而验证正确性. GKMMM18 采用了与BCCGP16[30]、Bulletproofs[31]等基于IPA 的零知识证明(见第7 章) 相似的方法, 即通过为QAP 中等式的每一项分别乘以变量n的某次幂从而将QAP 可满足问题转换为另外一个多项式是否为零多项式的问题. 具体的, 考虑多项式 若随机选取s、r, 计算等式(15)中f(s,r)·f(s,r) 可知,r7项的系数为 其中c0= 0, 而这恰为QAP 可满足问题的形式. 可以证明, 基于q阶单项式知识假设(q-monomial knowledge assumption) 和q阶单项式计算假设(q-monomial computational assumption)[41], 给定不含r7项的CRS, 若证明者可生成证明gA且有e(gf(s,r),hf(s,r)) =e(gA,h), 则可说明他拥有(cN+1,cN+2,··· ,cm). 类似的, 为说明gf(s,r)是正确构造的, 可引入另一个新变量w构造一个多项式f2(z,n,w) 使得当且仅当f(s,r) 正确构造时该多项式的某一特定项系数为0, 然后给定不含该特定项单项式的CRS, 利用双线性配对验证该多项式特定项系数确实为0. 在全局CRS 中,s、r、q分别对应于变量z、r、w. 在针对具体关系构造zk-SNARK 时, 需要对全局CRS 进行处理从而生成新的针对具体关系的CRS.与Pinocchio 等协议类似, 其生成方式也是构造用于验证QAP 的系列多项式, 其规模也为O(|C|) 级别的群元素. 协议流程. 在生成针对具体关系的CRS 后, GKMMM18 的协议流程简述如下. (1) 在给定QAP 四元组(t(z),U,W,У) 及群上生成元g1,g2后, 证明者P计算 其中多项式f3(s,r,q) 用于辅助验证f2(s,r,q) 中某一特定项系数为0. (2) 在收到证明π=(A,B,C) 后, 验证者验证 讨论总结. 首先分析安全性. 基于q阶单项式知识假设和q阶单项式计算假设[41], 如果验证者所验证的第二个等式成立, 那么可以得出证明者拥有形式正确的f(s,r,q) 且他拥有QAP 可满足问题的解, 即GKMMM18 可被证明具有知识可靠性. 另外, 由于δ的均匀随机性, 可以证明GKMMM18 具有完美零知识性. 其次分析复杂度. 如前文所述, GKMMM18 的全局CRS 规模为O(|CM|2) 级别的群元素, 针对具体关系的CRS 规模为O(|C|) 级别的群元素. 与Groth16 类似, GKMMM18 的通信复杂度也为3 个群元素, 证明复杂度也为O(|C|) 级别的群幂运算, 但验证复杂度比Groth16 多了一个配对运算. zk-SNARK 的通信复杂度为常数个群元素, 验证复杂度也可降低到常数个配对运算, 与区块链低存储、高吞吐的需求相契合, 大部分隐私保护应用如Zcash、以太坊扩容方案等也都是基于zk-SNARK 实现的. 然而, zk-SNARK 需基于不可证伪的非标准假设, 并且启动阶段的系统参数必须依赖可信第三方生成. 为解决这些问题, 出现了CRS 可更新的零知识证明, 还出现了系列底层假设更通用、启动阶段系统参数可公开生成的零知识证明, 这也被称为透明的zk-SNARK (transparent zk-SNARK), 本文将在第6–8章分别介绍三种启动阶段系统参数可公开生成的零知识证明. 本章介绍基于双向高效交互式证明(DEIP) 的零知识证明. 该类协议的核心思路是利用同态承诺、多项式承诺、随机掩藏多项式等技术将已有的针对电路求值问题的DEIP 转换为简洁NIZKAoK. 本章第6.1 节介绍相关定义及概念, 第6.2 节介绍背景及主要思路, 第6.3 节介绍典型协议. 多项式承诺(polynomial commitment, PC)[122]是对多项式的承诺. 除具有隐藏性和绑定性外, 发送者还可向接收者证明多项式f(·) 在某个由接收者随机选取的点t上的取值为y, 即f(t)=y. 本章涉及的多项式承诺均是针对多变量多项式的, 且允许交互(是Bünz 等人[123]对文献[122] 中多项式承诺的扩展). 定义27(多项式承诺[27,123]) 一个多变量多项式承诺方案PC = (Setup,Com,Open,Eval) 由以下4个算法组成. • pp←Setup(1λ,ℓ,d): 参数生成算法. 以安全参数λ的一元表示、多项式变量参数ℓ和度参数d为输入, 输出公共参数pp. • (c,s)←Com(pp,f(·)): 多项式承诺算法. 以公共参数pp 和多项式f(·) 为输入, 输出承诺c和打开提示s. •b ←Open(pp,c,f(·),s): 多项式承诺打开算法. 给定公共参数pp、承诺c、多项式f(·) 和打开提示s, 打开并验证承诺c的正确性, 输出接受(b=1) 或拒绝(b=0). •b ←Eval(pp,c,t,y,ℓ,d;f(·),s): 求值计算协议. PC.Eval 是一个交互式公开抛币协议, 拥有隐私输入f(·) 和s的证明者向验证者证明f(t)=y.V输出接受(b=1) 或拒绝(b=0). 如果一个PC 的求值计算协议是知识可提取的(见定义14), 则称该PC 是可提取的. 如果一个可提取PC 的求值计算协议是零知识知识论证, 且具有统计意义的证据扩展可仿真性, 则称该PC 是零知识的,记为zk-PC. 在本章中, PC 的主要作用是实现传输多项式的简洁性, 与PC 相同作用的另一个概念是可验证多项式委托(verifiable polynomial delegation, VPD)[124], 其允许用户将多项式f(·) 在若干点的求值计算外包给服务者, 同时服务者提供一个证明用以证明求值计算的正确性. 定义28(可验证多项式委托[28,51,125]) 一个针对多变量多项式f(·) 的可验证多项式委托VPD =(Setup,Com,Eval,Verify) 由以下4 个算法组成. • (pp,vp)←Setup(1λ,ℓ,d): 参数生成算法. 以多项式变量参数λ的一元表示、多项式变量参数ℓ和度参数d为输入, 输出公共参数pp 和验证陷门vp. •c ←Com(pp,f(·)): 多项式承诺算法. 以公共参数pp 和多项式f(·) 为输入, 输出承诺c. • (y,π)←Eval(pp,f(·),t,r): 求值计算算法. 以公共参数pp、多项式f(·)、多项式上的点t和随机挑战r为输入, 计算y=f(t), 输出求值y及证明π. •b ←Verify(vp,c,y,t,π,r): 验证算法. 以验证陷门vp、承诺c、求值y、多项式上的点t、求值证明π和随机挑战r为输入, 验证求值计算的正确性, 并输出接受(b=1) 或拒绝(b=0). 如果一个VPD 的求值计算算法不直接输出y而是输出对y的承诺comy(其能够“零知识地” 隐藏y且π可支持验证comy确实是对f(·) 的承诺), 则称该VPD 是零知识的, 记为zk-VPD. 定义28中的VPD 需要验证陷门vp, 因此启动阶段系统参数的生成须保持私密, 具体方案见文献[26,51]; 也有不需验证陷门的VPD, 其系统参数可公开生成, 具体方案见文献[28,29]. r1,r2,··· ,ri−1由V在前i −1 轮分别随机选取, 且可最终归约为对g(r) =g(r1,r2,··· ,rℓ) 的声明, 其中r ∈Fℓ. 当V拥有g(·) 时, 可自行计算g(r); 当g(·) 是秘密时,V可通过对谕示g(·) 的访问请求得到g(r). 该证明共有ℓ轮, 可靠性误差为O(mℓ/|F|) (由Schwartz-Zippel 引理保障), 通信量为O(mℓ) 个域元素, 验证者计算开销为O(mℓ) 级别的域上运算, 证明者计算开销为O(2ℓ) 级别的域上运算[126]. 相比于平凡计算求和函数的复杂度O(2ℓ), sum-check 协议的验证复杂度有显著降低. 6.2.1 背景 针对分层算术电路求值问题的双向高效交互式证明. Goldwasser 等人[61]利用sum-check 协议为核心组件, 提出了一个针对分层算术电路求值问题的的交互式证明. 由于证明和验证复杂度均较低, 该类协议又被称为双向高效的交互式证明(DEIP). 之后, Cormode 等人[60]利用多变量线性扩展代替了上述协议中的低度扩展(low-degree extension), 将上述协议的证明复杂度从O(poly|C|) 降低为O(|C|log|C|).后续对证明复杂度的一系列改进大多是在具有特殊结构的分层电路基础上实现的. 对于常规电路(regular circuit)[60], 即电路谓词(wiring predicates, 见第6.2.2 小节) 在任意点的取值都可在O(poly log|C|) 级别时间、O(log|C|) 级别空间内可计算的电路(对数空间均匀电路就是一种常规电路), Thaler[126]指出证明复杂度可以降低到O(|C|); 对于有着许多规模为|C′| 的相同子电路的数据并行电路(data parallel circuit), Thaler 同时指出证明复杂度可以降低到O(|C|log|C′|), 在此基础上, Wahby 等人[127]将证明复杂度继续降低到了O(|C|+|C′|log|C′|); 对于有着许多不直接连接且互不相同的子电路的电路, Zhang等人[125]提出了一种证明复杂度为O(|C|log|C′|) 的DEIP. 对于任意的分层算术电路, Xie 等人[26]提出了一种证明复杂度为O(|C|) 的变种DEIP. 需要注意的是, 上述协议所基于的电路均是分层算术电路. 交互式证明与零知识证明的转换. Cramer 等人[102]及Ben-Or 等人[128]给出了利用同态承诺将交互式证明转换为计算零知识证明或完美零知识论证的通用方法. 其核心思路是将交互式证明中证明者发送的信息用同态承诺掩藏. 该方案的安全性支撑有三: (1) 由于承诺的隐藏性, 验证者无法推知与被承诺信息相关的其他信息, 进而保障零知识性. (2) 由于承诺的绑定性, 证明者无法欺骗, 进而保障可靠性. (3) 由于承诺的同态性, 协议可以在保障零知识性的同时完成正确性验证. 6.2.2 主要思路 本小节首先介绍DEIP, 其次介绍基于Pedersen 承诺的零知识sum-check 协议, 最后介绍利用DEIP和零知识sum-check 协议如何构造基于DEIP 的平凡零知识证明. DEIP. 一种DEIP 的主要流程如协议3 所示. 令C是域F 上深度为d的分层算术电路, 记第0 层是电路输出线所在层, 第d层是电路输入线所在层. DEIP 逐层按轮运行. 在协议第1 轮, 当验证者V收到证明者P发送的输出y后,P和V调用sum-check 协议将对电路第0 层的声明转换为对电路第1 层的声明; 在协议第i轮,P和V调用sum-check 协议将对电路第i −1 层的声明转换为对电路第i层的声明; 最终,P和V将电路求值转换为对电路第d层(即输入层) 的声明, 由于V拥有电路输入x, 故可直接自行计算验证. 协议3 一种DEIP [26]公共输入: 域F, 深度为d 的分层算术电路C : F|x| →F|y|.1. P 向V 发送电路输出y.2. V 计算多项式~V0(·) 并返回随机挑战r0 ∈Fs0.3. P 和V 调用对~V0(r0) 的sum-check 协议. 在sum-check 协议的最后一轮, V 会收到~V1(u(1)) 和~V1(v(1)).4. for i = 1,2,··· ,d −1 V 选择随机挑战α(i),β(i)$←−F 并发送给P;P 和V 调用对α(i)~Vi(u(i))+β(i)~Vi(v(i)) 的sum-check 协议;在sum-check 协议的最后一轮, P 发送给~Vi+1(u(i+1)) 和~Vi+1(v(i+1)) 给V;V 利用~Vi+1(u(i+1)) 和~Vi+1(v(i+1)) 参与到第i+1 轮循环.end for 5. V 根据第d 层的输入x 自行计算~Vd(u(d)) 和~Vd(v(d)), 进而检查第d −1 轮的sum-check 协议的正确性.输出: 比特b, b = 1 表示V 检查通过, b = 0 表示拒绝. 具体的, 记电路C第i层的电路门数为Si且si=「log2Si⏋(假设Si是2 的某次幂, 若不是则可对电路作必要填充). 记Vi(·):{0,1}si →F 是以第i层的某个任意电路门的二进制顺序表示字符串{0,1}si为输入、该门的门值为输出的函数. 记addi(·),multi(·) :{0,1}2si+si−1→{0,1}为电路谓词, 其以第i −1 层某个电路门(记为αc) 的二进制顺序表示字符串{0,1}si−1、第i层的某两个电路门(记作αa,αb)的二进制顺序表示字符串{0,1}si为输入, 当且仅当电路中存在以αa、αb为输入,αc为输出的加法门(乘法门) 时输出为1. 基于以上定义, 对于任意的c ∈{0,1}si,a、b ∈{0,1}si+1,Vi(c) 可写为 这样就可将对第i层的声明归约为对第i+1 层的声明. 由于Vi(·) 是求和形式, 故可调用sum-check 协议进行验证. 然而,Vi(·) 的定义域大小为2, 基于Schwartz-Zippel 引理难以保障可靠性. 因此, 为调用sum-check 协议, 需将Vi(·) 转换为对应的多变量线性扩展多项式~Vi(·). 基于文献[26,60,61,126,127], 可以证明针对分层算术电路的系列DEIP 的可靠性误差根据协议的不同从O(dlogg/|F|) 到O(dlog|C|/|F|) 不等, 证明者计算开销为O(|C|) 到O(|C|log|C|) 级别的域上运算, 实际通信量为O(dlogg) 到O(dlog|C|) 级别的域元素. 对于常规电路, 验证者计算开销为O(|x|+|y|+dlogg) 到O(|x|+|y|+dlog|C|) 级别的域上运算. 当电路深度d=poly(log|C|) 时, DEIP系列协议的通信复杂度和验证复杂度均与电路规模成亚线性关系. 基于 Pedersen 承诺的零知识 sum-check 协议. 在sum-check 协议中, 验证者会获得多项式gi(Xi), 当g(·) 是秘密时, 会泄露g(·) 的相关信息, 故不是零知识的. 事实上, 基于Cramer 和Damgård[102]的方法, 利用Pedersen 承诺容易构造零知识的sum-check 协议. 在介绍零知识sum-check 协议之前, 首先给出利用Pedersen 承诺可实现的两个模块. 给定形如定义8的Pedersen 承诺方案, 则存在以下两个零知识论证. (1) 给定公共承诺c1←Com(x1;r1),c2←Com(x2;r2) 且x1=x2, 证明者可向验证者证明c1和c2是对相同消息的承诺, 即x1=x2, 记该论证为ZKeq(c1,c2). 具体协议及安全性证明见文献[130]. (2) 给定公共承诺c1←Com(x1;r1),c2←Com(x2;r2),c3←Com(x3;r3) 且x3=x1x2, 证明者可向验证者证明c1和c2的承诺消息乘积与c3的承诺消息乘积相等, 即x3=x1x2, 记该论证为ZKprod(c1,c2,c3). 具体协议及安全性证明见文献[32,131]. 基于上述两个模块, 容易将图6 中的协议修改为零知识的, 主要思路见协议4. 需要指出的是, 协议4是不考虑Pedersen 承诺中随机数的简化版本, 详细版本见文献[51]. 协议4 与图6 的主要不同在于: 图6 sum-check 协议流程[63]Figure 6 Process of sum-check protocol 相比于sum-check 协议, 零知识sum-check 协议的证明和验证复杂度虽然不变, 但实际证明和验证开销却因引入了大量群上运算尤其是群幂运算而显著增加. 协议4 基于Pedersen 承诺的零知识sum-check 协议的主要思路[51]公共输入: 域F,Com(T),m,ℓ. 证明者秘密输入: g(x), 且有T = ∑x∈{0,1}ℓ g(x).1. i = 1 时, 证明者P 构造函数g1(X1) 并将对其系数(a1,0,a1,1,··· ,a1,m) 的承诺Com(a1,0),Com(a1,1),··· ,Com(a1,m) (省略了Com 中的随机数) 发给验证者V.2. V 计算Com∗1 ←Com(a1,0)∏m j=0 Com(a1,j) 并调用ZKeq(Com∗1,Com(T)). 若ZKeq 验证失败, 输出b = 0;若验证通过, V 选取r1$←−F 发送给P.3. P 和V 共同计算Com2 ←∏m j=0 Comr1j(a1,j).4. for i = 2,3,··· ,ℓ −1 P 构造函数gi(Xi) 并将对其系数(ai,0,ai,1,··· ,ai,m) 的承诺Com(ai,0),Com(ai,1),··· ,Com(ai,m) 发给验证者V;V 计算Com∗i ←Com(ai,0)∏m j=0 Com(ai,j) 并调用ZKeq(Com∗i,Comi). 若ZKeq 验证失败, 输出b = 0; 若$←−F 发送给P;P 和V 共同计算Comi+1 ←∏m j=0 Comrij(ai,j).验证通过, V 选取ri end for 5. P 构造函数gℓ(Xℓ) 并将对其系数(aℓ,0,aℓ,1,··· ,aℓ,m) 的承诺Com(aℓ,0),Com(aℓ,1),··· ,Com(aℓ,m) 发给验证者V.6. V 计算Com∗ℓ ←Com(aℓ,0)∏m j=0 Com(aℓ,j) 并调用ZKeq(Com∗ℓ,Comℓ). 若ZKeq 验证失败, 输出b = 0;若验证通过, V 选取rℓ$←−F.7. V 计算Comℓ+1 ←∏m j=0 Comrℓj(aℓ,j). V 获知Com(g(r)) (可通过谕示) 并调用ZKeq(Comℓ+1,Com(g(r)).若ZKeq 验证失败, 输出b = 0.输出: 比特b, 若上述验证均通过, 输出b = 1; 否则输出b = 0. 基于DEIP 的平凡零知识证明利用基于Pedersen 承诺的零知识的sum-check 协议可构造基于DEIP 的平凡零知识证明(简要流程见图7), 其与协议3 主要不同在于: 图7 基于DEIP 的平凡零知识证明[32]Figure 7 Trivial zero-knowledge proof based on DEIP 基于DEIP 的平凡零知识证明可分为2 部分: (1) 在协议第一步, 证明者需对证据(α1,α2,··· ,α|w|) 及{αjαk}作承诺, 其中{αjαk}指所有存在乘法门关系的门值乘积集合; 在协议最后一步, 验证者需根据收到的承诺计算对(u(d)) 和(v(d)) 的承诺并验证sum-check 协议的正确性. (2) 调用d次零知识的sum-check 协议. 对于(2), 由于其只是将域上操作替换为承诺操作及同态运算, 且在普通DEIP 中不需要第(1) 步, 故其渐近复杂度与普通DEIP 是一致的, 但实际证明和验证开销有显著增加. 改进上述零知识证明基于DEIP 的平凡零知识证明主要存在如下三点问题: (1) 不是简洁的. 通信复杂度为(Θ(|w|)+O(dlogg)) 级别的群元素, 其中Θ(|w|) 来自于直接传输证据,O(dlogg) 来自于d次零知识sum-check 协议. (2) 实际计算开销大. 由于加性同态承诺中加法运算会转换为乘法运算, 乘法运算会转换成幂运算,利用加性同态承诺保障零知识性会显著增加实际证明和验证开销. (3) 待证明陈述表示形式(分层算术电路) 不够通用且需要预处理. 虽然通过增加电路深度级别的电路门, 任意算术电路都可转换为分层算术电路[32], 但是仍需对具体计算问题进行预处理. 近年来的研究在不同程度上解决了上述三点问题, 构造了若干基于DEIP 的简洁NIZKAoK, 其总结列于表5. 表5 中实现简洁性所采取方案指零知识多项式承诺(zk-PC) 及零知识可验证多项式委托(zk-VPD), 其用于解决问题(1). 根据多项式承诺或可验证多项式委托方案(列于表6)的不同, 各协议的底层难题假设和可信初始化情况也各不相同. 随机掩藏多项式用于解决问题(2), 由于基于的DEIP 不同, 各协议支持的电路问题形式也不尽相同. Spartan (针对R1CS 可满足问题) 和Virgo++ (针对任意算术电路) 用于解决问题(3). 本章第6.3 节分别介绍解决上述问题的零知识证明. 表5 基于DEIP 的简洁NIZKAoK 总结Table 5 Succinct non-interactive zero-knowledge arguments of knowledge based on DEIP 本节介绍基于DEIP 的零知识证明典型协议(见图8), 分析各协议的主要思路、协议流程、复杂度及安全性. 根据对基于DEIP 的平凡零知识证明的改进思路及方法的不同, 第6.3.1 小节介绍ZKvSQL 和Hyrax, 其主要改进是利用zk-PC 和zk-VPD 传输证据多项式, 从而实现简洁性. 第6.3.2 小节介绍Libra和Virgo, 其主要改进是在ZKvSQL 和Hyrax 的基础上改用掩藏多项式而不是加性同态承诺实现零知识sum-check 协议, 这减少了大量的群幂运算从而降低了实际证明与验证开销. 第6.3.3 小节介绍Spartan,其待证明陈述形式是R1CS 可满足问题, 需注意的是严格而言Spartan 并不是基于DEIP 构造的, 但其与基于DEIP 的零知识证明思路极为类似, 故在本章介绍. 第6.3.4 小节介绍Virgo++, 其在Libra 和Virgo的基础上改进了DEIP, 从而将待证明陈述形式扩展为任意算术电路. 图8 基于DEIP 的零知识证明典型协议优化思路Figure 8 Optimization of typical zero-knowledge proof based on DEIP 6.3.1 ZKvSQL/Hyrax 主要思路. ZKvSQL 由Zhang 等人[51]提出, Hyrax 由Wahby 等人[32]提出, 它们的主要思路是利用zk-VPD 和zk-PC 改进图7 证明者的第一步操作, 从而实现简洁性, 其使用的zk-VPD 及zk-PC 方案列于表6. 考虑到表6 中的方案承诺大小|c| 和通信复杂度均为亚线性, 且d次零知识sum-check 协议的通信复杂度为O(dlogg), 因此当d=O(poly log|C|) 时, 可实现通信复杂度为亚线性的零知识证明. 表6 针对多变量线性多项式的零知识可提取多项式承诺方案对比Table 6 Comparison of several zero-knowledge extractable polynomial commitment schemes for multilinear polynomials 讨论总结. 现从复杂度和安全性两个方面对ZKvSQL 和Hyrax 进行讨论总结. (1) 现给出利用zk-PC 实现简洁NIZKAoK 的复杂度分析, 其开销主要分为d次零知识sum-check协议的开销和参与多项式承诺的开销, 各项开销具体如下. • 证明复杂度. 证明者需要: 参与d次零知识sum-check 协议, 其与普通DEIP 的证明复杂度是同级别的, 记该部分计算复杂度为PDEIP; 对多项式~w(·) 作承诺及参与求值计算协议, 记该部分计算复杂度为PPC. • 通信复杂度. 通信开销包括:d次零知识sum-check 协议所需传输的信息, 其与DEIP 本身的通信复杂度相同, 记该部分通信复杂度为πDEIP; 传输对~w(·) 的承诺带来的通信开销和求值计算的通信开销, 记该部分通信复杂度为πPC. • 验证复杂度. 验证者需要: 参与d次零知识sum-check 协议, 其与普通DEIP 的验证复杂度是同级别的, 记该部分计算复杂度为VDEIP; 参与对多项式~w(·) 的求值计算, 记该部分计算复杂度为VPC. 根据不同零知识证明所采取的不同DEIP 和zk-PC, 基于各参数的关系, 协议的证明、通信和验证复杂度详见表7. 表7 利用不同DEIP 和zk-PC 实现零知识知识论证的复杂度分析Table 7 Complexity analysis of zero-knowledge argument of knowledge based on different DEIPs and zk-PC schemes (2)安全性分析. ZKvSQL 和Hyrax 的底层难题假设主要来自于其调用的zk-PC,也就是说,ZKvSQL基于的假设是q-SDH 假设和(d,ℓ)-EPKE 假设, Hyrax 基于的假设是DLOG 假设. 协议的可靠性来自于zk-PC 的绑定性、DEIP 本身的可靠性和sum-check 协议中加性同态承诺的绑定性. 协议的知识可靠性来自于zk-PC 的可提取性. 协议的零知识性来自于zk-PC 的隐藏性、zk-PC 中求值计算协议的零知识性和加性同态承诺的隐藏性. 6.3.2 Libra/Virgo 主要思路. Libra 由Xie 等人[26]提出, 相比于第6.2.2 小节中的平凡DEIP, 在利用zk-PC 实现简洁性的基础上, Libra 利用随机掩藏多项式降低了零知识sum-check 协议的证明和验证计算开销. 在此基础上, Zhang 等人[28]提出了一种新的多项式承诺(表6 中的Virgo-VPD) 并将其应用于Libra 中, 实现了一种启动阶段参数可公开生成的NIZKAoK, 即Virgo. 本小节主要介绍Libra 的主要思路和协议流程. 在sum-check 协议中, 证明者发送给验证者的消息是与电路相关的多项式gi(Xi), 这有可能会破坏零知识性. 基于Pedersen 承诺的零知识sum-check 协议虽可解决这一问题, 但大量的群幂运算会显著增加证明和验证计算开销. 在此背景下, Chiesa、Forbes 和Spooner[129]指出为sum-check 协议中的多项式g(·) 增加随机多项式ρf(·) 即可实现零知识性, 其中ρ是由验证者选择的随机挑战. 此时证明者和验证者是对多项式g(·)+ρf(·) 调用sum-check 协议. 假设形如定义27的zk-PC 存在, 零知识sum-check 协议具体见协议5, 其省略了公共参数pp、验证陷门vp 和随机数. 然而, 利用上述零知识sum-check 协议难以直接构造基于DEIP 的零知识证明, 这是因为在DEIP 中第i轮sum-check 协议的最后一轮,V会获得~Vi(u(i)) 和~Vi(v(i))(对应于协议5 中的g(r)), 这会泄露一定的隐私信息. 为了解决这一问题, Chiesa、Forbes 和Spooner 进一步指出为~Vi(·) 增加一个随机掩藏低度多项式Ri(·) 可实现零知识性. 具体来说, 定义多项式 其中当且仅当x=y时I(x,y)=1, 否则I(x,y)=0. 协议5 Libra 中的零知识sum-check 协议[26]公共输入: 域F,T,m,ℓ.证明者秘密输入: g(x), 且有T = ∑x∈{0,1}ℓ g(x).1. 证明者P 随机选取多项式f(x), 其中每个变量的度也为m. P 将F = ∑x∈{0,1}ℓ f(x) 和对f(·) 的承诺comf = Com(f(·)) 发给验证者V.2. 验证者V 选取ρ$←−F 发送给P 并计算T +ρF.3. P 和V 调用对T +ρF 的sum-check 协议.4. 在sum-check 协议的最后一轮, V 收到hℓ(r) = g(r)+ρf(r), 然后打开多项式承诺comf 获取f(·) 在点r = (r1,r2,··· ,rℓ) 处的值.5. V 计算hℓ(r)−ρf(r) 并验证其与从谕示获得的g(r) 是否相等.输出: 比特b, 若上述验证均通过, 输出b = 1; 否则输出b = 0. 协议流程. Libra 与Virgo 的协议流程与ZKvSQL 和Hyrax 基本一致. 不同的是, Libra 和Virgo不再需要使用加性同态承诺, 而是采用随机掩藏多项式ρf(·) 和R(·) 实现零知识性, 其中ρf(·) 用于保障sum-check 协议中证明者发送给验证者的信息是不泄露隐私的,R(·) 用于保障sum-check 协议最后的谕示也是不泄露隐私的. 不过, 为了防止恶意证明者利用R(·), 证明者需在协议开始时发送对R(·) 的多项式承诺. 讨论总结. 现分别从复杂度和安全性两个方面对Libra 和Virgo 进行讨论总结. (1) Libra 的复杂度. 与第6.3.1 小节类似, Libra 的复杂度开销也可分为两部分, 即d次零知识sumcheck 协议的开销和多项式承诺的开销. Libra 中的零知识sum-check 协议不再需要使用加性同态承诺, 而是调用zk-PC 对电路每一层的掩藏多项式进行承诺, 因此不再需要大量的群幂运算. 然而为实现整个协议的零知识性, 需额外对d个变量数为2 且每个变量度为2 的多项式调用zk-PC. 因此Libra 中的PPC和VPC需分别对应增加O(d), 其具体复杂度列于表7. (2) Virgo 的复杂度. Zhang 等人指出在分析Virgo 的复杂度时, 可将调用zk-PC 的开销分为对电路输入层(变量数为log|in|=log(|x|+|w|)) 调用承诺的开销和对电路中间层调用承诺的开销,他们分别优化了这两者的渐近性质, 并指出相比于d次sum-check 协议的开销, 对电路中间层调用承诺的开销在渐近复杂度上可以忽略. 因此Virgo 的复杂度开销包括d次sum-check 协议的开销和对电路输入层调用zk-PC 的开销两部分, 其具体复杂度列于表7. (3) 安全性分析. 同ZKvSQL 和Hyrax 类似, Libra 和Virgo 的底层难题假设主要来自于其调用的zk-PC, 也就是说, Libra 基于的假设是q-SDH 假设和(d,ℓ)-EPKE 假设, Vrigo 基于的假设是CRHF 存在性. 协议的可靠性来自于zk-PC 的绑定性、DEIP 本身的可靠性. 协议的知识可靠性来自于zk-PC 的可提取性. 协议的零知识性来自于zk-PC 的隐藏性、zk-PC 中求值计算协议的零知识性和sum-check 协议的零知识性. 6.3.3 Spartan 上述协议所针对的待证明陈述表示形式均是分层算术电路, 同时为实现简洁性和亚线性的验证复杂度, 需要对电路有更多的要求, 比如电路深度d不能太大, 电路是常规电路、数据并行电路等. 一个改进方向就是设计待证明陈述表示形式更为通用的零知识证明. 其中, Setty[27]提出了Spartan, 一种针对R1CS 可满足问题的简洁NIZKAoK, 由于R1CS 可满足问题是高级语言编译器的常见目标程序[62,65]且任意C-SAT 问题都可用R1CS 可满足问题表示[27], 因此相比于针对分层算术电路可满足问题的零知识证明, Spartan 的待证明陈述更为通用. 事实上, 严格而言Spartan 并不是基于DEIP 构造的, 但其与基于DEIP 的零知识证明思路极为类似, 故在本章介绍. 此外, Zhang 等人[29]提出了Virgo++, 其是直接针对任意算术电路可满足问题的简洁NIZKAoK. 本小节介绍Spartan, 第6.3.4 小节介绍Virgo++. 主要思路. Spartan 的设计思路如图9 所示. 图9 Spartan 的主要思路[27]Figure 9 Main idea of Spartan 首先介绍编码R1CS 可满足问题的思路. 为借鉴之前利用sum-check 协议构造零知识证明的思路, 需将R1CS 可满足问题编码为低度多项式. 考虑形如定义3的R1CS 组, 令s=「log2m⏋, 则矩阵A,B,C可视为函数A(·,·),B(·,·),C(·,·) :{0,1}s×{0,1}s →F. 类似的, 令zT= (io,1,w), 则zT也可以视为函数Z(·):{0,1}s →F. 定义函数F(x):{0,1}s →F 由于对于任意的t ∈{0,1}s, 有Q(t) = ~F(t), 因此上述R1CS 组是可满足的当且仅当对于任意的t ∈Fs, 有Q(t)=0, 即Q(·)是零多项式. 由Schwartz-Zippel 引理, 对于随机挑战τ$←−Fs, 若Q(τ)=0,则有较大的概率说明Q(·) 是零多项式, 且有s=O(logm) =O(logn). 又Q(τ) 为求和形式, 故可调用sum-check 协议验证Q(τ)?=0. P将vA,vB,vC发送给V, 随后P和V还需再次调用sum-check 协议验证等式(29) 是否成立, 并将验证这三个等式归约为验证 6.3.4 Virgo++ Virgo++ 由Zhang 等人[29]提出, 他们的主要贡献是提出了一种针对任意算术电路的DEIP 并将其应用于Virgo 中, 进而得到了一种针对任意算术电路可满足问题的简洁NIZKAoK. Virgo++ 的协议流程和安全性分析均与Virgo 类似, 本小节仅简要介绍Virgo++ 中的DEIP, 并给出简单的复杂度分析. 主要思路. Zhang 等人指出制约系列DEIP 效率的最主要因素之一就是DEIP 只能应用于分层算术电路. 在渐近级别上, 将任意电路转化为分层算术电路会将电路规模从O(|C|) 增加到O(d|C|); 在实际工程应用中, 将任意电路转化为分层算术电路会增加证明者1–2 个数量级的计算开销[29]. 此外, 将任意电路转换为R1CS 也不够高效. 基于以上背景, Zhang 等人提出了一种针对通用算术电路且不额外增加证明者计算开销的DEIP, 并采用Virgo 中的方法将DEIP 转换为简洁NIZKAoK. Virgo++ 中DEIP 构造的主要思路如下. 虽然通用电路没有严格的分层结构, 但仍可以进行逻辑意义上的分层, 即一个电路门的输入门的层级一定比该电路门高. 考虑到第i层的任意电路门α一定至少有一条输入导线位于i+1 层(否则该门就不可能位于第i层), 而另一条输入导线可能位于(i+1)∼d的任意一层,因此电路层i的多项式规模为O((d−i)g). 基于此思想可构造证明复杂度为O(d|C|)的DEIP,这是因为证明者调用sum-check 协议的复杂度为O(dg+(d −1)g+···+g)=O(d2g)=O(d|C|). 此外, 在电路层i,P还需在调用sum-check 协议完毕后将对O((d −i)g) 级别多项式取值的声明转换为1 个声明,该阶段的复杂度也起码为O(d|C|). 上述平凡方法与将任意电路转换为分层算术电路的渐近复杂度是至少一样的, 也就没有实际意义. 针对上述两个问题, Zhang 等人分别提出了两个解决方案. 对于前一个问题,他们指出由于每层电路门的输入门最多为为2g, 因此调用sum-check 协议的复杂度可降低至O(dg). 对于后一个问题, 他们指出可将转换声明的计算归约为运行一个针对特定分层算术电路的普通DEIP, 由于归约后协议轮数为O(|C|), 因此该阶段的证明复杂度也为O(|C). 基于以上两点改进, Zhang 等人实现了针对通用算术电路且证明复杂度为O(|C|) 的DEIP, 并最终将其转换为了简洁NIZKAoK. 协议流程. Virgo++ 的协议流程与Virgo 的协议流程基本一致, 即在DEIP 的基础上, 利用多项式承诺实现简洁性, 利用随机掩藏多项式和zk-PC 保障零知识性. 不同的是, Virgo++ 中DEIP 所针对的电路可以是任意的算术电路. 讨论总结. Zhang 等人提出的DEIP 的性能表现分析如下. 对于规模为|C|、输入长度为|x|、深度为d的通用电路,该协议可靠性误差为O(dlog|C|/F),证明复杂度为O(|C|),通信复杂度为min{O(dlog|C|+d2),O(|C|)}. 当电路为常规电路时, 验证复杂度为min{O(|x|+|y|+dlog|C|+d2), O(|C|)}. 基于该DEIP, 结合Virgo 的复杂度分析方法, 可以得出Virgo++ 的各项复杂度, 其列于表5. 基于DEIP 的零知识证明是本文涉及的唯一一种可实现证明复杂度与电路规模成线性关系、通信和验证复杂度与电路规模成亚线性关系的系统参数可公开生成的零知识证明, 但也存在若干限制. 第一, 由于DEIP 按层计算的特性, 只有针对深度较低的电路该类零知识证明的通信复杂度才与电路规模成亚线性. 因此, 能否及如何削弱电路深度的线性因子影响是未来的一个研究方向. 第二, 由于DEIP 对于特殊结构的电路, 比如对数空间均匀电路或者数据并行电路才能快速验证的特性, 只有针对特殊结构的电路,验证复杂度才与电路规模成亚线性. 本章介绍基于内积论证(IPA) 的零知识证明. 该类零知识证明的底层难题假设均基于离散对数假设(见定义32), 故也被称为基于离散对数假设的零知识证明. 然而为便于与其他基于离散对数假设的零知识证明加以区分(如Hyrax, 见第6.3.1 小节), 且由于内积论证是实现该类协议对数级别通信复杂度的关键技术, 故本文将该类协议称为基于IPA 的零知识证明. 该类协议的核心思路是将电路中的所有约束归约转化为内积形式的陈述, 然后调用内积论证实现对数级别通信复杂度的简洁NIZKAoK. 本章第7.1 节介绍相关定义及概念, 第7.2 节介绍该类协议的背景及主要思路, 第7.3 节介绍典型协议. 其中,Un-Find-Rep 假设可归约为DLOG 假设, 离散对数关系假设[30]与Un-Find-Rep 假设等价. 此外, 可以证明ML2v-Find-Rep 假设可归约为A-DLOG 假设[54]. 基于Linear-PCP 的零知识证明虽然实现了较低的通信和验证复杂度, 但具有若干缺点, 其中之一就是底层难题假设均为不可证伪假设. Groth 和Seo 提出的协议虽然仅基于离散对数假设并具有更高的安全性, 但通信复杂度仍较高. 在此基础上, Bootle 等人[30]提出了内积论证并利用其构造了对数级别通信复杂度的NIZKAoK (记为BCCGP16). 证明者通过内积论证可利用循环递归的方式证明他拥有两个公开向量承诺的消息, 且这两个消息的内积等于某个公开值. 对于长度为n的消息向量, 内积论证的通信复杂度为O(logn). 本小节接下来介绍内积论证的主要思路及其优化. 内积论证. 在BCCGP16 的内积论证中,证明者P可向验证者V证明对于公共输入A,B ∈G,g,h ∈Gn和公开标量z ∈Zq,P拥有向量a、b, 满足A=ga、B=hb和a·b=z. 该陈述可记为 其中分号前后分别表示公共输入和证据. 若g,h的生成方式为g ←[r],h ←[s], 则陈述(33)可改记为 协议6 BCCGP16 中的内积论证[30]公共输入: (G,q,g,[r],[s],A,B,z).证明者秘密输入: a,b.1. P 向V 发送A−1,B−1,z−1,,A1,B1,z1, 具体有A−1 ←[a 1 2 ·r 2 2],B−1 ←[b 1 2 ·s 2 2],z−1 ←a 2 2 ·b 1 2,A1 ←[a 2 2 ·r 1 2],B1 ←[b 2 2 ·s 1 2],z1 ←a 1 2 ·b 2 2.2. V 向P 发送随机挑战c$←−Z∗q.3. P 和V 共同计算新的承诺密钥[r′],[s′] 和新承诺A′,B′ 及z′[r′] ←[c−1r 1 2 +c−2r 22],A′ ←AAc−1−1 Ac1,[s′] ←[cs 1 2 +c2s 2 2],B′ ←Bc−1BBc−1 1 ,z′ ←z−1c+z +z1c−1.4. P 计算下一轮的新证据a′ ←ca 1 2 +c2a 2 2 和b′ ←c−1b 1 2 +c−2b 22 并参与到下一轮循环中, 此时待证明陈述被归约为{([r′],[s′],A′,B′,z′;a′,b′) : A′ = [a′ ·r′]∧B′ = [b′ ·s′]∧a′ ·b′ = z′}.5. 上述循环归约过程共重复t = log2 n 次, 直至a 和b 缩减为标量, 此时P 只需直接将a 和b 发给V 然后V 自行验证如下等式是否成立即可At?= [a·rt],Bt?= [b·st],zt?= a·b,其中At,Bt 表示第t 轮中的承诺, [rt] 和[st] 表示第t 轮的承诺密钥. 为证明陈述(37), Bulletproofs 首先证明了如下形式的陈述 然后证明了陈述(37). 证明陈述(38)的主要思路也是在每一轮将对n长向量的陈述递归为对n/2 长向量的陈述, 具体见协议7. 在该内积论证中, 每轮需要传输的群元素仅为2 个(L和R), 且最后一轮需额外发送a和b共2 个域元素, 故总通信量为(2 log2n+2) 个元素. 证明者计算开销与BCCGP16 类似, 为O(n) 次群上运算; 但验证者每轮不再需要计算[r′]、[s′] 而只需计算A′、B′, 但需额外验证2 个配对等式, 故为O(logn) 次群上运算和配对运算. 对于安全性, 与BCCGP16 类似, Bulletproofs 中的内积论证也具有完美完备性和统计意义的证据扩展可仿真性. 协议7 Bulletproofs 中的内积论证[31]公共输入: (G,q,[r],[s],P,u), 其中P,u ∈G.证明者秘密输入: a,b, 其满足P = [a·r][b·s]ua·b.1. P 计算L,R ∈G 并向V 发送L,R, 其中L ←[a 1 2 ·r 2 2][b 2 2 ·s 1 2]ua 1·b 2 2 2,R ←[a 2 2 ·r 1 2][b 1 2 ·s 2 2]ua 2·b 1 2 2.2. V 向P 发送随机挑战c$←−Z∗q.3. P 和V 共同计算新的承诺密钥[r′],[s′] 和新承诺P′, 其中[r′] ←[c−1r 1 2 +cr 2 2],[s′] ←[cs 1 2 +c−1s 2 2],P′ ←Lc2 ·P ·Rc−2.4. P 计算下一轮的证据a′ ←ca 1 2 +c−1a 2 2 和b′ ←c−1b 1 2 +cb 2 2 并参与到下一轮循环中. 此时新承诺密钥为[r′]和[s′], 归约后的陈述为{(G,q,[r′],[s′],P′,u;a′,b′) : P′ = [a′ ·r′][b′ ·s′]ua′·b′}.5. 协议共重复t = log2 n 轮直至a 和b 缩减为标量, 此时P 只需直接将a 和b 发给V 然后V 自行验证本轮的Pt 是否满足Pt = [a·rt][b·st]uab 即可. Zhang 等人[134]指出相比于BCCGP16 中的内积论证, 虽然Bulletproofs 中的内积论证具有较低的总通信量, 但修改陈述会使得其应用条件相对苛刻. 针对此, Zhang 等人在不修改陈述的前提下将BCCGP16 中内积论证的通信复杂度降低了约2/3. 相比于Bulletproofs, Zhang 等人的内积论证虽然总通信量较高, 但其应用条件和BCCGP16 一样宽松. DRZ20[54]指出在承诺密钥g和h结构化, 即r和s具有特殊分布的情况下, 可将协议6 的验证复杂度降低到对数级别. 然而为保障协议的可靠性, 密钥需由可信第三方生成, 也就是说该内积论证需要CRS. 其他轮类似. 此时验证者在每轮只需进行常数级别的配对运算, 故验证复杂度是对数级别的. 此外, 每轮验证形如等式(40) 的等式也意味着相比于BCCGP16 每轮P需额外发送[r′1]1,[s′1]1共2 个元素, 故通信复杂度为(8 log2n+2) 个元素. 与BCCGP16 类似, 证明者计算开销也为O(n) 级别的群上和域上运算,DRZ20 中的内积论证也具有完美完备性和统计意义的证据扩展可仿真性. 基于内积论证的零知识证明的主要构造思路为: 首先将电路中的乘法门约束和乘法门之间的线性约束利用Schwartz-Zippel 引理归约为一个多项式的某一特定项系数为零的问题, 然后将该问题转化为内积论证的陈述表示形式, 最后调用内积论证实现零知识证明. 事实上, 由于上述过程中前两个步骤是较为简单的, 对该类零知识证明的改进大都与内积论证的改进紧密相关, 相关协议总结列于表8, 各协议优化思路见图10. 基于第7.2 节中涉及到的三种内积论证, 本章第7.3.1 小节介绍BCCGP16, 第7.3.2 小节介绍Bulletproofs 和HKR19, 第7.3.3 小节介绍DRZ20. 图10 基于IPA 的零知识证明典型协议优化思路Figure 10 Optimization of typical zero-knowledge proof based on inner product argument 表8 基于IPA 的简洁NIZKAoK 总结Table 8 Succinct non-interactive zero-knowledge arguments of knowledge based on IPA 7.3.1 BCCGP16 主要思路与协议流程BCCGP16 中交互式简洁零知识知识论证的主要思路与协议流程如图11 所示,说明如下. 图11 BCCGP16 的主要思路与协议流程[30]Figure 11 Main idea and process of BCCGP16 (1) 在协议交互之前, 证明者P将算术电路所有的门约束分为乘法门约束和不同乘法门之间的线性约束. 对于乘法门约束,P将电路中所有乘法门的左输入a、右输入b和输出c排布为m×n的矩阵A,B,C,其中左输入矩阵A的每一行分别记为(a1=(a1,1,a1,2,··· ,a1,n),··· ,am=(am,1,am,2,··· ,am,n)), 矩阵B,C同理. 这样, 电路中的乘法门约束就可记为A ⊙B=C, 共有mn=|CM| 个等式. 对于不同乘法门之间的线性约束, 其可记为对于q ∈[Q], 有 其中wq,a,i,wq,b,i,wq,c,i为常向量,Kq为常标量. 例如,假设电路中仅有一个加法门且门的左输入、右输入、输出分别为2a1,1、a1,2、b1,1,则此时Q=1,m=1,w1,a,1=(2,1,0,··· ,0),w1,b,1=(−1,0,··· ,0),K1=0, 等式(41)等价于2a1,1+a1,2−b1,1=0. 由于每个乘法门最多有两个输入, 因此线性约束等式最多有Q ≤2mn个. 为同时验证mn+Q个等式,P将这些等式归约为一个多项式p(Y), 其思路是为每个等式逐个乘Y的j次幂,j ∈[mn+Q]. 具体的, 构造 用于验证乘法门约束, 构造 用于验证线性约束. 此时C-SAT 问题被归约为p(Y) =pM(Y) +pL(Y) 是否为零多项式的问题. 由Schwartz-Zippel 引理, 验证p(Y) =pM(Y)+pL(Y) 是否为零多项式可通过选取随机挑战y$←−Zp然后验证p(y)?=0 实现, 其可靠性误差约为(mn+Q)/|F|. (2) 在协议交互阶段, 首先P发送对证据向量{ai,bi,ci}i∈[m]的承诺. 其次, 在收到第一次随机挑战y后,P构造洛朗多项式t(X) 使得t(X) 的常数项为p(y), 并构造对去除t(X) 常数项的多项式t′(X) 的多项式承诺. 其中t(X) =r(X)· r′(X)−2K(y) 为内积形式. 一个t(X) 的例子见本小节BCCGP16 的平凡改进部分. 具体而言,r(X) 可由{ai,bi,ci}i∈[m]计算得出, Com(r(X)) 也可由Com(ai),Com(bi),Com(ci) 计算得出;r′(X)=r(X)⊙(ym,y2m,··· ,ynm)+2s(X)、s(X) 和K(y) 均由电路结构和随机挑战决定. 也就是说, 只需给出r(x) 验证者就可自己构造r′(x)、K(y). 最后, 在V发送第二次随机挑战x后,P将r(x) 发送给V并利用多项式承诺揭示t′(x) 的值. 由于直接发送r(x) 可能泄露隐私信息, 为保障零知识性, 需引入盲化向量d对r(X) 进行盲化, 故第一轮还需发送对盲化向量d的承诺. (3) 在检查阶段,V首先利用承诺的同态属性, 验证r(x) 与利用第一轮收到承诺构造的r(x) 是一致的; 然后根据电路结构和y自行计算s(x),K(y), 并计算t(x)←r(x)· r′(x)−2K(y), 最后验证t′(x)?=t(x). 若验证通过, 则由Schwarz-Zippel 引理可知左式以极高的概率等于右式, 又右式与左式之差即为t(X) 的常数项p(y), 故可说明p(y) 有极高的概率为0, 因此协议的可靠性得以保障. 上述协议最后需直接发送向量r(x). BCCGP16 指出可不直接发送r(x) 而发送对r(x),r′(x) 的承诺并调用内积论证验证t′(x)?=r(x)·r′(x)−2K(y), 进而降低通信复杂度. 事实上, 对r(x),r′(x) 的承诺也可由V根据对{ai,bi,ci}i∈[m],d的承诺、电路结构及随机挑战自行算出. 故此时的通信开销仅包含利用多项式承诺揭示t′(x) 及内积论证所需要的通信量, 分析如下. 如果调用内积论证, 协议会增加log2n轮. 此时P的计算开销会因为内积论证增加O(|CM|) 级别的群上运算.V的计算开销主要分为打开对多项式t′(x) 的承诺, 基于承诺的同态属性计算对r(x)、r′(x) 和s(x) 的承诺和参与内积论证, 而这均需要O(|CM|) 级别的群上运算. 而对于通信复杂度, 在满足mn=|CM| 的条件下, 将m设置为2、n设置为|CM|/2 时通信量可达到最低, 为(6 log|CM|+13) 个元素(包括群元素和域元素). 其次分析安全性. 基于DLOG 假设, BCCGP16 是具有完美完备性、完美特殊诚实验证者零知识性和统计意义的证据扩展可仿真性的零知识论证. 对于完美完备性, 若算术电路所有的门约束都是可满足的,则多项式p(Y) 是零多项式, 进而可得洛朗多项式t(X) 没有常数项, 故最终验证者会接受证明. 对于完美特殊诚实验证者零知识性, 可构造一个模拟器S, 其输入公开陈述和验证者的挑战, 随机生成证明中的部分群或域元素, 并利用验证方程计算证明中的其余元素, 输出模拟证明, 使得该证明与诚实证明者生成的证明具有完美不可区分的分布. 该属性由承诺的隐藏性和盲化向量d保障. 对于统计意义的证据扩展可仿真性, 可构造一个提取器X, 其根据数量多项式于安全参数的可接受副本提取出有效的证据. 该属性由承诺的绑定性和内积论证的证据扩展可仿真性保障. BCCGP16 的平凡改进. 事实上, BCCGP16 中将证据向量a、b和c排布为矩阵是非必要的, 后续研究[31,53,54]等也均是直接对a ⊙b=c进行约束转化的. 在这种设置下, 等式(41)–(43)可相应消除与m相关的子式. 此时, 等式(42)可改记为 等式(41)可改记为 等式(43)可改记为 对于t(X), 有 容易验证,t(X) 的常数项为2p(y)=2(p′M(Y)+p′L(Y)). 此外,t(X) 的度为6, 故对其承诺不再需要使用多项式承诺而只需分别对每一项系数进行承诺, 这有助于降低证明者的计算开销. 7.3.2 Bulletproofs/HKR19 主要思路. Bulletproofs 的主要思路如图12 所示. 与BCCGP16 类似, Bulletproofs 的主要思路也是先将n=|CM| 个乘法门约束和Q个线性约束归约为一个多项式约束, 即p(Y,Z) 是否为零多项式; 然后将该多项式约束转换为内积形式陈述, 即t(X)=∑tiXi=L(X)·R(X) 中t2=p(y,z) 是否为0; 随后就可构造Com(t(x)) 和缺失t2项的Com(t′(x)) 并验证上述两个承诺相等从而说明p(Y,Z) 是零多项式, 而内积论证可保障承诺是正确构造的. 与BCCGP16 不同的是, Bulletproofs 中向量多项式t(X) 的度为常数, 这与对BCCGP16 的平凡改进思路一致. 图12 Bulletproofs 的主要思路与协议流程[31]Figure 12 Main idea and process of Bulletproofs 此外, 上述过程并不是零知识的, 这是因为在调用内积论证时V可能会获得部分秘密信息(V起码会在内积论证的最后一轮获得秘密的组合). 为实现零知识性, 可引入随机向量sL、sR并在L(X)、R(X)分别增加sLX3项和(yn ⊙sR)X3项, 考虑到引入随机向量不会改变t2, 因此其可在不影响完备性的同时保障零知识性. 协议流程基于以上主要思路, Bulletproofs 协议流程(见图12 所示) 简要描述如下, 其中Com(a,b)表示形如gahbhr的承诺, 其中r$←−F. 讨论总结. 首先分析复杂度.P的计算开销包括构造多项式p(Y,Z) 和t(X), 具体为O(|C|) 级别的域上运算; 承诺向量aL、aR等, 具体为O(|CM|) 级别的群上运算.V的计算开销包括利用承诺构造P和构造承诺Com(t′(x))、Com(t(x)), 具体为O(|CM|) 级别的群上运算. 相比于BCCGP16, Bulletproofs的总通信量可降低到(2 log2|CM|+13) 个元素4其中, 调用内积论证需传输的(2 log|CM|+5) 个元素(确定陈述需3 个, 内积论证过程需(2 log|CM|+2) 个), 协议流程的第(1) 步需传输3 个承诺值, 第(2) 步需传输5 个承诺值.. 然后分析安全性. 与BCCGP16 类似, Bulletproofs 具有完美完备性、完美特殊诚实验证者零知识性和计算意义的证据扩展可仿真性. 对于完美完备性, 若算术电路所有的门约束都是可满足的, 则多项式p(Y,Z) 是零多项式, 进而可得多项式t(X) 的二次项系数t2为0, 故最终验证者会接受证明. 对于完美特殊诚实验证者零知识性, 可构造一个模拟器S, 其输入公开陈述和验证者的挑战, 随机生成证明中的部分群或域元素, 并利用验证方程计算证明中的其余元素, 输出模拟证明, 使得该证明与诚实证明者生成的证明具有完美不可区分的分布. 该属性由承诺的隐藏性和盲化向量sL、sR保障. 对于计算意义的证据扩展可仿真性, 可构造一个提取器X, 其根据数量多项式于安全参数的可接受副本, 以不可忽略的概率提取出有效的证据. 该属性由承诺的绑定性和内积论证的证据扩展可仿真性保障. HKR19 指出R1CS 是二次等式约束的一种特例, 并且相比于用二次等式表达电路, 利用R1CS 表达电路需要更多的中间变量和等式, 因此在一定程度上会增加证明者的计算开销[53]. 基于以上发现, HKR19 首先借鉴BCCGP16 和Bulletproofs 中的内积论证构造了零知识的内积论证, 然后利用零知识内积论证构造了零知识的二次等式集合论证, 并沿用Bulletproofs 的主要思路构造了针对C-SAT 问题的简洁NIZKAoK. 实验仿真表明, HKR19 中的零知识论证的实际通信量和实际验证计算开销与Bulletproofs 基本相同, 实际证明计算开销比Bulleptroofs 少约1/4. 7.3.3 DRZ20 主要思路. DRZ20[54]实现了CRS 可更新的证明复杂度为线性、通信和验证复杂度均为对数级别的简洁NIZKAoK, 其验证复杂度在渐近级别上的突破主要依赖于结构化承诺密钥, 而CRS 用于保障结构化承诺密钥的私密性. 对于验证复杂度, DRZ20 指出BCCGP16 中验证者V的复杂度成线性的原因有三: 协议流程. DRZ20 的协议流程与BCCGP16 的协议流程是类似的, 简要描述如下. (1) 将C-SAT 问题归约为p(Y) =pM(Y)+pL(Y) 为是否为零多项式的问题. 其形式如第7.3.1 小节的等式(44) 和等式(45). (2) 证明者P将对证据a、b、c和盲化向量d的承诺发送给验证者V. 与BCCGP16 不用的是, 此时的承诺为可更新的Pedersen 向量承诺, 为实现可更新性, 需在CRS 中相应引入验证密钥. (3) 在V发送随机挑战y后,P构造多项式t(X)使得t(X)的常数项为p(y),t(X)形式如等式(49).P构造缺失常数项的多项式t′(X) 并发送对其的多项式承诺. (4) 在V发送随机挑战x后,P通过多项式承诺揭示t′(x) 的值, 然后P和V调用对t(x) 的内积论证. 与BCCGP16 不同的是, 此时的内积论证为基于结构化承诺密钥的对数级别验证复杂度的内积论证. 为保障可靠性, 需在CRS 中相应引入验证密钥. 此外, 为实现对数级别的验证复杂度,需将计算s(x) 的任务委托给证明者, 故证明者在该步还需给出对s(x) 的承诺并附带一个零知识证明, 其用于证明s(x) 是正确构造的. 讨论总结. 基于A-DLOG 和q-A-DLOG 假设,DRZ20 具有完美完备性、完美特殊诚实验证者零知识性和统计意义的证据扩展可仿真性. 相比于其他可更新的零知识证明方案[23,40,42,120], DRZ20 不再需要系列知识假设和代数群模型(algebraic group model), 但在CRS 长度、通信和验证复杂度上有所牺牲(特别的, 通信复杂度从常数群元素级别提升至对数级别). 具体的, DRZ20 中可更新的简洁NIZKAoK 的证明开销为(22+10M)n′E1,通信量为(12 logn′E1+8 logn′P),验证开销为(12 logn′G1+4 logn′F),其中m指电路中的导线数目,M是描述预处理电路输入输出导线数目上限的参数(预处理电路由P构造用于委托计算s(X)),n′是预处理电路的规模, 其满足n′≤n+(2m/M −1). 在Sonic[40]中,n′=3|CM|,M=3. 此外,E、P分别指群幂运算和配对运算,E1指非对称群中群G1上的群幂运算, G、F 分别指对应群和域中的元素. 对于实际性能,由于引入了双线性群,相比于其他不需配对的同类零知识证明,DRZ20会带来一定的性能损失. 基于IPA 的零知识证明具有以下优点: (1) 底层难题假设更为通用. 均基于DLOG 假设及其变种, 属于标准假设. (2) 应用场景多元. 除实现对C-SAT 问题的证明外, 基于IPA 还可构造低实际通信量的范围证明[31](range proof)、洗牌正确性证明(proof of correctness of a shuffle)[53,135]、向量置换证明[54](vector permutation proof) 等, 在区块链密码货币场景下应用广泛. 然而, 该类零知识证明的验证复杂度为线性, 验证时由于引入了大量的群幂运算也会导致实际验证开销较大. 值得注意的是, DRZ20 虽然实现了验证复杂度在渐近级别上的突破, 但需要承诺密钥结构化并引入CRS 用于保障密钥分布的正确性. 本章介绍基于MPC-in-the-Head 的零知识证明. 该类协议的构造思路是证明者在脑海中模拟运行一个针对零知识函数的安全多方计算协议, 然后将协议运行过程中的视图发送给验证者, 验证者验证视图正确性, 而协议的零知识性由MPC 协议的隐私性保障. 本章第8.1 节介绍相关定义及概念, 第8.2 节介绍该类协议的背景及主要思路, 第8.3 节介绍典型协议. 定义33(安全多方计算[136]) 安全多方计算(secure multiparty computation, MPC) 可使独立参与方在不信任彼此及第三方的情况下, 基于各自的秘密输入共同计算某个目标联合函数, 且计算期间不泄露除计算结果外的其他额外信息. 记安全多方计算协议为Πf, 目标联合函数为f(x,w1,r1,··· ,wn,rn),其中公共输入为x, 参与方P1,P2,··· ,Pn的秘密输入分别为w1,w2,··· ,wn、随机输入分别为r1,r2,··· ,rn. 参与方Pi在协议运行第j+1 轮时发送的消息可由消息确定函数Π(i,x,wi,ri,(m1,m2,··· ,mj)) 决定, (m1,m2,··· ,mj) 分别代表参与方Pi前j轮收到的消息向量. 若消息向量包含k个不同参与方的消息(包括Pi), 就称消息确定函数Π 为k元. 记参与方Pi的视图为Vi, 其包含wi,ri及Pi在协议运行过程中收到的所有消息. 参与方Pi的本地输出可由其视图Vi确定, 记为fi(x,Vi). 在本章中,只考虑各参与方的本地输出与目标联合函数相等的情况, 即 安全多方计算的敌手模型分为半诚实敌手模型和恶意敌手模型. 半诚实敌手会诚实地运行协议, 但会通过分析其他参与方的消息试图获得与诚实参与方秘密输入相关的信息; 而恶意敌手可以在协议运行过程中实现任意高效攻击, 如控制参与方发送消息、拒绝其他参与方的消息、篡改消息等. 本章中出现的MPC协议均处于半诚实敌手模型下. 一个安全多方计算协议Πf的完美正确性(perfect correctness) 是指随机数r1,r2,··· ,rn的选取不会影响目标函数计算结果的正确性, 即 一个安全多方计算协议Πf的t-隐私性(t-privacy) 是指t个半诚实敌手无法获得与诚实参与方秘密输入相关的其他信息. 具体的, 称安全多方计算协议Πf具有t-隐私性. 如果对于任意输入(x,w1,r1,··· ,wn,rn) 及任意腐化参与方集合T(满足|T|≤t), 都存在一个PPT 模拟器S, 使得腐化参与方的联合视图分布与模拟器生成的分布相同, 即 一个安全多方计算协议的r-鲁棒性(r-robustness) 是指如果R(x,w)̸= 1, 那么即使r个恶意敌手也无法使诚实参与方输出接受. 一个安全多方计算协议的视图一致性[98](consistency of view) 是指对于任意的视图对(Vi,Vj),x和Vi所确定的由参与方Pi发给Pj的消息与视图Vj所表明的此消息是一致的. 反之亦然. 定义34(交织里德-所罗门码[35]) 对正整数n和k, 域F 及向量ξ= (ξ1,ξ2,··· ,ξn)∈Fn, RS 码L= RSF,n,k,ξ是[n,k,d] 线性码, 其形式为(p(ξ1),p(ξ2),··· ,p(ξn)), 其中p(·) 是度小于k的多项式, 记为码多项式. 由于任意两个度小于k的域上多项式最多有k −1 个交点, 因此码距d最小为n −k+1. 若L ⊂Fn是[n,k,d] 线性码, 则交织码(interleaved code)Lm是定义在Fm×n上的[n,mk,d] 线性码. 具体的, 该码可排列成m×n的码矩阵U, 该码矩阵的每一行ui满足ui ∈L, 即第i行的表示形式为(pi(ξ1),pi(ξ2),··· ,pi(ξn)), 其中pi(·) 是度小于k的多项式. 基于交织码, 交织里德-所罗码的定义自然可得, 简记为IRS 码. 在本章中, 由于Ligero 系列协议[35,36,48]中码矩阵U可被视为信息论安全证明中的谕示, 因此也被称为谕示矩阵. 定义35(利用IRS 码加密消息[35]) 给定η=(η1,η2,··· ,ηℓ) (ℓ ≤k) 及RS 码L=RSF,n,k,ξ, 对长为ℓ的消息向量x= (x1,x2,··· ,xℓ) 的加密即为码(pu(ξ1),pu(ξ2),··· ,pu(ξn)), 其中pu(·) 是码u对应的码多项式, 且满足对于任意的i ∈[ℓ],pu(ηi) =xi. 给定码矩阵U的每一行u1,u2,··· ,um, 对消息向量x= (x11,x12,··· ,x1ℓ,··· ,xm1,xm2,··· ,xmℓ) 的加密即为码(pu1(ξ1),pu1(ξ2),··· ,pu1(ξn),···,pum(ξ1),pum(ξ2),··· ,pum(ξn)). 8.2.1 背景 零知识证明与MPC 在多个层面存在紧密联系. 在协议内涵层面, 零知识证明可以视为恶意敌手模型下的一种两方特殊MPC 协议[136]. 在该协议中, 证明者和验证者共同拥有问题的陈述x, 证明者还拥有证据w, 证明者试图在不泄露证据的同时证明R(x,w) = 1. 该协议中目标联合函数f(x,w,r1,r2) =R(x,w), 验证者是敌手, 其目标是获取与证据w相关的其他隐私信息. 在协议构造层面, 零知识证明可用于构造MPC 协议, MPC 也可用于构造零知识证明. 针对前者,Goldreich、Micali 和Wigderson[137]利用零知识证明给出了一种在不更改目标联合函数的同时将半诚实敌手模型下的MPC 协议转换为恶意敌手模型下的MPC 协议的通用方法. 针对后者, 又分为基于混淆电路(garbled circuits) 的零知识证明和基于MPC-in-the-Head 的零知识证明. Jawurek、Kerschbaum 和Orlandi[138]于2013 年提出了一种基于混淆电路的零知识证明, 该类证明不需要底层的混淆电路具有隐私性而只需其具有可认证性(authenticity) 和可验证性(verifiability), 因此Frederiksen、Nielsen 和Orlandi[139]将该类协议称为免隐私的混淆方案(privacy-free garbling scheme).后续工作如文献[140,141] 从通信复杂度、底层难题假设等方面优化了上述零知识证明. 由于该类证明的通信复杂度均与陈述规模和证据大小成线性, 故不是简洁的, 本章不再详述. Ishai 等人[98]于2007 年提出了一种基于MPC-in-the-Head 的零知识证明, 后续工作具体实现了该协议[33], 并从通信复杂度、可靠性等角度进行了改进[34–36,47]. 该类零知识证明只需对称密钥操作、不需要可信初始化、通信复杂度可达到亚线性级别、实际证明速率较快, 具有较高的理论价值和较为广泛的应用前景. 8.2.2 主要思路 Ishai 等人提出的零知识证明主要思路如协议8 所示. 证明者首先在脑海中模拟一个MPC 协议的运行, 得到每个参与方的视图, 证明者随后对每个视图作承诺, 并将这些承诺发给验证者; 然后验证者挑选2个随机挑战; 其次证明者打开这2 个承诺; 最后验证者验证一致性和正确性. 该协议具有完美完备性, 其源于Πf的完美正确性; 具有可靠性, 其源于Πf的完美正确性和敌手模型的半诚实; 具有零知识性, 其源于2-隐私性. 对于零知识性, 由于验证者V拥有2 个参与方的视图, 其本质上相当于一个腐化了2 个参与方并试图获取其他隐私信息的半诚实敌手, 这与2-隐私性的内涵是一致的. 事实上, 该证明的模拟器就是调用2-隐私性的模拟器构造的. 协议8 IKOS07 协议[98]公共输入: 陈述x 和MPC 协议Πf, 其中Πf 具有完美正确性和2-隐私性. 给定一个多项式时间内可判定的二元关系R 及其对应的NP 语言L(R), 目标联合函数f 与L(R) 满足条件: 对于任意的x、任意的w = w1 ⊕w2 ⊕···⊕wn 和r1,r2,··· ,rn, 有f(x,w1,r1,··· ,wn,rn) = R(x,w1 ⊕w2 ⊕···⊕wn).证明者输入: w, 满足R(x,w) = 1.1. P 将证据w 随机分为n 份w1,w2,··· ,wn, 随后在脑海中模拟以x 为公共输入、以w1,w2,··· ,wn 为各参与方隐私输入、以r1,r2,··· ,rn 为各参与方随机输入的MPC 协议Πf. 协议运行完毕后, P 会得到n 个参与方的视图V1,V2,··· ,Vn, 他分别承诺这n 个视图, 即生成随机数s1,s2,··· ,sn, 然后计算Com(V1;s1),Com(V2;s2),··· ,Com(Vn;sn), 并将这n 个承诺发送给V.2. V 随机挑选两个参与方i,j$←−[n], 并将i,j 发送给P.3. P 将Vi,si,Vj,sj 发送给验证者.4. V 验证如下三项并输出比特b: (1) 第3 步收到的消息与第1 步收到的承诺是一致的. (2) 参与方Pi 和Pj 的本地输出fi(x,Vi) 与fj(x,Vj) 皆为1. (3) 参与方Pi 和Pj 的视图Vi 和Vj 是一致的. 如果上述三项未均通过, 则选择拒绝输出: 比特b, b = 1 代表V 接受, b = 0 代表V 拒绝. 基于MPC-in-the-Head 的零知识证明运行MPC 协议的效率与运行普通MPC 协议的效率存在一定的差别. 在MPC-in-the-Head 环境下, 证明者可以免费利用OT 信道[98](bblivious transfer channel) 及任意的二元确定函数[33](特定条件下的n元确定函数也可以[47]), 这是因为证明者只需脑海中模拟, 而无需真正运行MPC 协议, 这也就省去了部分计算和通信开销. 因此, 虽然该类零知识证明的证明复杂度为线性或准线性级别, 但实际证明开销通常并不大. 对于证明复杂度以外的性能表现,针对实现非交互的方式,该类零知识证明是Σ 协议,故可通过ROM下的Fiat-Shamir 启发式转换为非交互零知识证明; 针对是否抗量子及需要公钥加密, 该类零知识证明是基于PCP、IPCP 或IOP 构造的, 调用合适的MPC 协议[137,142,143]即可实现只依赖对称密钥操作且抗量子的零知识证明. 事实上对该类零知识证明的优化主要集中在降低通信复杂度, 且根据通信复杂度渐近级别的不同, 该类零知识证明可分为两类, 协议总结如表9 所示, 具体描述如下. 第一种是通信复杂度为O(|C|) 的零知识证明, 包括表9 中的ZKBoo[33]、ZKB++[34]、KKW18[47]和Limbo[49]. 协议8 的通信量为(n·|Com|+t(|F|+|V|+|s|)), 其中|Com| 指承诺的大小,t为打开视图数目,|F| 指域元素的大小,|V| 指视图规模,|s| 指随机数的大小, 因此通信复杂度主要由参与方数目和视图规模决定. 考虑视图规模, 对于一个目标联合函数为电路求值且基于加性秘密分享的MPC 协议, 各参与方分别持有每条电路输入导线的秘密分享份额. 为了保障MPC 协议的正确性和安全性, 每个参与方视图在每个电路门处都需要存储一个秘密分享份额, 否则要么无法正确得到电路计算结果, 要么最多n−1个半诚实敌手就可破坏隐私性, 这就意味着每个参与方的视图规模至少为O(|C|). 表9 基于MPC-in-the-Head 的(简洁) NIZKAoK 总结Table 9 (Succinct) non-interactive zero-knowledge arguments of knowledge based on MPC-in-the-Head 事实上, 第一个可实现的基于MPC-in-the-Head 的零知识证明ZKBoo[33]的通信复杂度为O((n −1)2|C|). 这是因为ZKBoo 的底层MPC 协议是GMW 协议[137], 其需要参与方两两交互, 每个视图规模为O((n −1)|C|), 且协议共需打开n −1 个视图. 记目标可靠性误差为2−σ, 则ZKBoo 的通信复杂度约为σ·|C|(n −1)2/(log2n −1), 其中n ≥3. 由于该函数是递增函数, 因此n= 3 时通信复杂度最低,此时可靠性误差为2/3, 故协议在实际运行过程中需要重复较多轮数. ZKB++[34]虽然将ZKBoo 的实际通信量降低了约一半, 然而其仍与n有关, 可靠性误差也为2/3. 一个改进方向就是设计通信复杂度与n无关的MPC 底层协议, 这样就可以通过增加参与方个数n来降低可靠性误差进而降低总通信量. 基于此, KKW18[47]设计了一个针对布尔电路、消息确定函数为n元、视图打开个数为n −1 的MPC 协议. 在KKW18 中, 对于打开的n −1 个视图, 每个视图的规模与n无关, 此时可靠性误差为1/n. 当然, 为了验证协议的正确性与一致性, 第n个参与方的广播消息仍需要由证明者发给验证者, 此消息级别为O(|C|), 故协议的通信复杂度仍为O(|C|). 与上述思路不同的是, Limbo[49]基于Client-Server 模型构造了一种较为适合MPC-in-the-Head 的MPC 协议, 实现了通信复杂度虽为O(|C|)、但实际性能良好的NIZKAoK. 通信复杂度为O(|C|) 的工作有两个共同特征, 第一是均调用了基于加性秘密分享的MPC 协议, 每个参与方的视图规模与电路规模成线性关系; 第二是除加性秘密分享带来的约束之外, 参与方的视图之间仅有电路约束关系. 本节介绍基于MPC-in-the-Head 的零知识证明典型协议, 分析各协议的构造思路、协议流程、复杂度及安全性, 各典型协议优化思路如图13 所示. 本节第8.3.1 小节介绍ZKBoo 和ZKB++, 第8.3.2 小节介绍KKW18, 第8.3.3 小节介绍Ligero 和Ligero++, 第8.3.4 小节介绍BooLigero, 第8.3.5 小节介绍Limbo. 图13 基于MPC-in-the-Head 的零知识证明典型协议优化思路Figure 13 Optimization of typical zero-knowledge proof based on MPC-in-the-Head 8.3.1 ZKBoo/ZKB++ ZKBoo 由Giacomelli、Madsen 和Orlandi[33]提出, 是第一个可实现的基于MPC-in-the-Head 的NIZKAoK. ZKBoo 的底层MPC 协议是GMW 协议[137], 其消息确定函数为2 元、消息传播方式点对点、视图打开个数为n −1. 可以证明参与方数目n=3 时ZKBoo 的实际通信量最低. 主要思路. ZKBoo 设计了一个(2,3)-函数拆解方案((2,3)-function decomposition), 即对于计算电路的某个目标函数f:F|w|→F, 可将其拆解为3 个计算分支, 并且任意揭示2 个计算分支不会泄露与秘密输入w相关的其他信息. 此函数拆解方案本质上是GMW 协议[137]在算术电路下的变种, 即一种基于加性秘密分享的2-隐私性MPC 协议. ZKBoo 的拆解方案如图14 所示, 在该方案中证明者P的步骤主要包括: (1) 将证据w利用加性秘密分享(图14 中的Share) 随机分为w1,w2,w3共3 份, 并分发给相应参与方. (3) 在脑海中模拟各参与方将本地电路输出份额值广播, 并在获取其他方的份额后恢复电路最终输出值的过程(图14 中的Recover). 图14 ZKBoo [33](2,3)-函数拆解方案5Figure 14 (2,3)-function decomposition of ZKBoo 由于wi是随机生成的, 且消息确定函数是二元函数, 故获取其中2 个计算分支既能检查正确性和一致性, 又不会泄露第3 个参与方的秘密输入信息. 具体的, 对于输入为第x个门、第y个门、输出为第z个门的加法门, 任意的i ∈[3], 下式成立 对于输入为x、y, 输出为z的乘法门, 任意的i ∈[3], 下式成立 其中si表示第i个参与方的伪随机种子,R(·,·) 表示以对应种子和对应电路门为输入生成的随机数,i和i+1 均为模3 剩余. 协议流程ZKBoo 的协议流程如图15 所示, 其分为证明者生成承诺、验证者挑战、证明者响应、验证者检查四个阶段, 具体过程如下. 图15 ZKBoo 流程图[33]Figure 15 Process of ZKBoo 讨论总结. 现分别从可靠性、零知识性、复杂度和改进方向对ZKBoo 和ZKB++ 进行讨论总结. (1) 可靠性. 在ZKBoo 中, 一个恶意的证明者可以通过伪造参与方视图或者破坏视图一致性来欺骗验证者. 考虑伪造证据w′且R(x,w′) = 0, 若恶意证明者不破坏视图一致性, 则由MPC 协议的完美正确性, 验证者一定会发现错误. 若恶意证明者破坏视图一致性, 考虑最有利于欺骗成功的情况, 即恶意证明者仅破坏一对视图的一致性, 此时可靠性为1/3, 可靠性误差为2/3. 因此ZKBoo 的可靠性误差为2/3. (2) 零知识性. 考虑ZKBoo 逐门更新视图和计算电路的过程, 参与方的隐私信息就是每个电路门值的秘密分享份额, 只要不泄露该份额即可满足零知识性. 对于加法门, 各参与方可以本地更新视图, 故零知识性可自然保障. 对于乘法门, 计算参与方e的视图Ve时需要参与方e+1 的视图Ve+1, 而Ve+1又与Ve+2相关, 因此验证者获取视图Ve和Ve+1时可能会获取与Ve+2相关的隐私信息, 这违背了隐私性, 从而破坏了零知识性. ZKBoo 解决该问题的方法是为消息确定函数增加随机输入(等式(59)中的R(·)), 该随机输入能够在保障正确性的同时实现视图的均匀分布, 进而实现特殊诚实验证者零知识性. (3) 知识可靠性. ZKBoo 是一个3 轮Σ 协议, 并且具有3-特殊可靠性. 给定3 个接受副本(a,1,z1),(a,2,z2),(a,3,z3), 由于承诺的绑定性,z1和z3中包含的视图V1是一致的. 同理,z1和z2中包含的视图V2,z2和z3中包含的视图V3也是一致的. 在拥有V1,V2,V3后,可分别计算w1←V1[0],w2←V2[0],w2←V3[0], 然后恢复w ←w1+w2+w2, 从而提取出证据w. (4) 复杂度. 对于证明复杂度, 证明者需在脑海中模拟电路的计算过程并调用O(|C|) 次消息确定函数, 故证明复杂度为O(|C|); 对于验证复杂度, 验证者需在验证过程中重新计算电路, 故验证复杂度也为O(|C|); 对于通信复杂度, 当n确定时, 通信量主要由视图Ve和Ve+1决定, 而视图规模均为O(|C|), 故通信复杂度也为O(|C|). (5) 改进方向. 对于通信复杂度, ZKBoo 和ZKB++ 在采用加性秘密分享计算电路时会生成n个大小为O(|C|) 副本, 若视图打开数目为n −1, 则通信复杂度为O((n −1)|C|), 其与参与方数目n和电路规模|C| 有关, 而n又与可靠性误差有关. 在ZKBoo 和ZKB++ 中, 为实现最低的通信复杂度, 需取n= 3, 而这会使得可靠性误差为2/3. 因此, 相比于其他零知识证明, 为达到同样的目标可靠性误差, ZKBoo 和ZKB++ 需重复运行较多的轮数, 导致较高的实际通信量. 一个优化方向是采用合适的MPC 协议将生成视图的过程交与验证者, 使通信复杂度中的|C| 项与n无关, 从而通过降低可靠性误差来降低运行轮数进而优化通信复杂度, 而这恰好就是KKW18 的主要思想. 8.3.2 KKW18 KKW18 由Katz、Kolesnikov 和Wang[47]提出, 其底层MPC 协议出自文献[143], 该协议消息确定函数为n元、视图打开个数为n −1. 主要思路. KKW18 虽然也是逐门计算电路, 但是在该协议中各参与方的份额本质上是均匀分布的随机数, 可由伪随机生成器生成, 故对于打开的n −1 个视图, 可以仅发送对应的随机种子(长度仅与安全参数有关) 即可检查正确性和一致性. 该思想与ZKB++ 内涵是一致的, 即可由验证者计算出的视图不需要发送. 需要注意的是, 采用n元消息确定函数并不是自然的, 因为检查正确性时需要第n个参与方的相关信息, 而获取该相关信息又可能违背n-隐私性进而破坏零知识性. 针对这一问题, KKW18 采用了预处理模型下的MPC 协议(MPC protocol in the preprocessing model), 使份额的生成与电路的计算相互独立,进而保障了零知识性. 底层MPC 协议KKW18 中的MPC 模型为预处理模型, 可分为预处理阶段和在线阶段, 其具体流程如图16 所示. 在给定具体描述前, 首先介绍加性秘密分享的参数记法. 记[·] 表示加性秘密分享的份额,[·]i特指参与方Pi的份额. 对于电路中每条导线,n个参与方拥有一个(n,n) 的随机秘密分享掩藏份额和一个公开的掩藏值. 记zα为布尔电路C在导线α处的值, ˆzα为公开掩藏值, [λα] 为秘密分享掩藏份额,其恢复值为λα, 则zα满足zα= ˆzα ⊕λα. 图16 KKW18 底层MPC 协议流程图[47]Figure 16 Process of MPC protocol in KKW18 (1) 预处理阶段. 预处理阶段各参与方以伪随机种子和辅助输入为输入, 生成各输入导线值及电路门值的秘密分享掩藏份额. 对于输入导线α, 各参与方获得份额[λα]. 对于输入导线为a、b, 输出导线为c的异或门, 各参与方获得秘密掩藏份额[λa],[λb] 并自行计算生成[λc]←[λa]⊕[λb]. 对于输入导线分别为a和b、输出导线为c的与门, 各参与方获得份额[λa,b], 其满足λa,b=λa·λb.在预处理阶段, 份额[λ] 是均匀随机的, 因此可由伪随机种子s ∈{0,1}κs生成. 需要注意的是,前n −1 个参与方的秘密掩藏份额[λa,b] 虽然也可由该法生成, 但第n个参与方Pn的λa,b需要长为|C| 的辅助输入aux 才能保证[λa,b]=λa·λb成立. (2) 在线阶段. 在线阶段各参与方以输入导线的公开掩藏值ˆz为输入, 结合输入导线和各自持有的秘密分享掩藏份额, 计算电路中所有导线的公开掩藏值. 对于异或门, 参与方可本地计算公开掩藏值对于与门, 参与方需本地计算[y] 并将其广播, 之后每个参与方才能得到该与门的公开掩藏值. 各参与方逐门更新, 在计算得到输出导线的公开掩藏值ˆz之后, 他们就广播各自输出导线的秘密分享掩藏份额[λ] 并最终恢复输出导线值. 现对上述MPC 协议进行总结. 首先, 若证明者诚实运行协议, 由于秘密分享掩藏份额是在公开掩藏值之前生成的, 因此它们是互相独立的. 其次, 上述MPC 协议仅需在计算与门和恢复电路最终输出导线值时广播本地计算值[y], 且各参与方计算广播值时不需要交互, 故在整个协议中一个参与方最多需要传输|CA|+1 个比特, 其中|CA| 表示电路中与门的个数. 最后, 在拥有参与方Pi的伪随机种子si及可能需要的辅助输入(仅针对Pn) 后, 该参与方的广播值可自行算出. 协议流程在零知识证明中调用上述MPC 协议时, 每条输入导线值和每个电路值的秘密分享掩藏份额[λ]就是各参与方持有的隐私信息, 其在预处理阶段生成, 本质上是均匀分布的随机数; 公开掩藏值ˆz于在线阶段生成, 是每个参与方的公共输入. 若协议诚实运行, 由于[λ] 在ˆz之前生成, [λ] 与ˆz是独立的. 与一般3 轮Σ 协议不同的是, KKW18 协议为5 轮. 事实上, 前3 轮和后3 轮可分别视为2 个Σ 协议, 且第3 轮为重用轮. 在前3 轮, 证明者生成m份预处理信息, 验证者只选取其中1 份用以完成后续证明; 在后3 轮, 验证者打开n个参与方中的n −1 份视图以验证正确性和一致性. 具体流程如图17 所示(省略了承诺中的随机数), 简述如下. 图17 KKW18 协议流程图[47]Figure 17 Process of KKW18 (1)P生成m份对预处理状态的承诺, 并计算对该m份承诺的哈希. (2)V发送第一次挑战, 即对预处理状态承诺的随机挑战. (3)P响应第一次挑战, 打开m −1 份承诺.P在脑海中模拟与未打开的预处理阶段适配的在线阶段, 生成n份对广播信息的承诺, 并计算对该n份承诺的哈希. (4)V发送第二次挑战, 即对在线阶段广播信息承诺的随机挑战. (5)P响应第二次挑战, 将随机挑战值对应的预处理状态承诺和广播信息及剩余n −1 组的预处理信息发送给V. 验证者进行如下三项检查, 当且仅当检查全部通过后接受.利用步骤(5) 中n −1 组预处理状态生成承诺, 结合步骤(5) 中收到的预处理状态承诺构造hc, 验证与步骤(1) 中哈希h的一致性.利用步骤(5) 中{statec,i}i̸=p计算{msgi,i̸=p}, 结合msgp和{ˆz}重新计算电路输出并验证正确性.利用广播信息{msgi}i∈[n]计算哈希, 验证广播信息与步骤(3) 中哈希h′的一致性. 讨论总结. 现分别从知识可靠性、零知识性和复杂度对KKW18 进行讨论总结. (1) 知识可靠性. 假定抗碰撞哈希函数存在和承诺具有绑定性, 给定对于挑战对(c,p)、(c′,∗) 和(c,p′) 的接受副本, 其中∗为任意值, 且c ̸=c′,p ̸=p′, 则可提取出有效证据w, 其可靠性误差为max{1/m,1/n}[47]. (2) 零知识性. 与ZKBoo 及ZKB++ 类似, KKW18 的零知识性也是由秘密分享掩藏份额的随机性保障的. 不同的是, KKW18 中的消息确定函数为n元, 打开n −1 个视图是无法验证协议正确性的, 为验证正确性还需要第n个参与方的广播信息msgn, 而该信息可能泄露隐私. 解决该问题的方法是在预处理模型下分阶段运行MPC 协议, 从而保证秘密分享掩藏份额分布均匀且与公开掩藏值保持独立. 具体的, 对于某个输入导线为a、b, 输出导线为c的与门, 由于公共掩藏值ˆza、ˆzb与秘密分享掩藏份额[λ]a、[λ]b是独立的, 因此即使获取参与方Pp的广播信息[y]p(见图16)也难以推知导线a、b的秘密分享掩藏份额. 而参与方Pp的广播信息msgp恰好就是其在所有与门处的广播信息{[y]p}, 因此KKW18 的零知识性得以保障. 为确保证明者生成的秘密分享掩藏份额是均匀随机且与公开掩藏值是独立的, 需要在原有Σ 协议的基础上增加两轮对预处理阶段的检查(图17 中的前两步), 故协议共为5 轮. (3) 复杂度. 该协议的证明和验证复杂度与ZKBoo 及ZKB++ 类似, 均为O(|C|). 对于通信复杂度, 该协议的通信开销主要集中于协议流程的步骤(5), 其中处理与门信息的通信量期望大小为(n −1)·(|C|/n+κs) 比特, 广播通信规模至多为|CA|+1 比特,|CA| 为电路中与门的个数. 因此, 协议的单轮通信复杂度为O(|C|+nκs). 相比于ZKB++ 和Ligero (见第8.3.3 小节), 针对与门数为300-100 000 的布尔电路可满足问题, KKW18 实现了证明的最低实际通信量. 8.3.3 Ligero/Ligero++ 主要思路. Ligero 的主要思路如图18 所示. 证明者P首先将秘密输入(x,y,z,we) 排列为矩阵, 然后利用RS 码编码矩阵的每一行得到谕示矩阵, 接着利用默克尔树对谕示矩阵的每一列进行承诺, 最后P与V参与交互式协议用以证明电路是可满足的. 其中, RS 码保证了V在获取谕示矩阵每行的部分值后也不能恢复整个多项式所以也无法得到电路其他位置的导线值, 而RS 码的线性纠错性质保障了不符合电路约束的导线值会以较高的概率被V发现. 图18 Ligero 主要思路及协议流程图[35]Figure 18 Main idea and process of Ligero 协议流程在交互式协议中, 证明者和验证者需调用若干测试模块. 测试模块分为: (1) 对IRS 码的检查, 该模块可用于检查谕示矩阵U与其对应的IRS 码Lm的距离是否小于e, 其中e与IRS 码的码距d有关, 在Ligero 中, 有e (2) 对IRS 码中线性约束的检查. 在模块(1) 成立的情况下, 该模块可验证某IRS 码U加密的消息向量x ∈Fmℓ×1是否满足某线性关系Ax=b, 其中A ∈Fmℓ×mℓ,b ∈Fmℓ×1. (3) 对IRS 码中二次约束的检查. 在模块(1) 成立的情况下, 该模块可验证IRS 码Ux,Uy,Uz加密的消息向量x,y,z是否满足二次关系x ⊙y+a ⊙z=b, 其中a,b ∈Fmℓ×1. 上述三个测试模块的主要思路也列于图18. 首先证明者P发送对谕示矩阵的承诺(用默克尔树实现,图18 中的Root), 其次验证者V发送随机挑战r1,r2,··· ,rm, 接着P返回谕示矩阵行多项式与挑战值的线性组合多项式p(·), 然后V发送第二次随机挑战ξ1,ξ2,··· ,ξt, 最后P将谕示矩阵的这t列及其对应的默克尔树路径发送给V. 此时V验证以下三项: (1) 结合默克尔树路径, 验证打开的t列与承诺Root 是一致的. (2) 验证组合多项式p(·) 在点ηi,i∈[ℓ]处是否满足电路约束, 即验证IRS 码的对应消息向量满足电路约束. (3) 验证组合多项式p(·) 与谕示矩阵中随机选取的t列是一致的. 需要指出的是, 上述测试模块的可靠性均是由RS 码的线性纠错性质保障的. 同时, 这些测试模块的检查过程本质上是一种IPCP. 其中, 谕示矩阵是谕示, 随机挑战是访问请求. 借助上述测试模块, Ligero 的交互式论证简要流程如下. (1) 输入阶段. 记算术电路为C: F|w|→F, 证明者P拥有秘密输入w= (α1,α2,··· ,α|w|) 使得C(w)=1. 记电路中门数为|C|, 其门值分别记为β1,β2,··· ,β|C|. (2) 码矩阵生成阶段. 记m,ℓ满足m·ℓ ≥|w|+|C|,P首先生成扩展证据we ∈Fmℓ×1,we满足前|w|+|C| 个值为(α1,α2,··· ,α|w|,β1,β2,··· ,β|C|). 其次P构造向量x,y,z ∈Fmℓ×1且其满足第j个值分别对应第j个乘法门的左输入、右输入及输出. 再次P构造二次约束检查矩阵Px,Py和Pz ∈Fmℓ×mℓ, 其满足 然后P构造线性约束检查矩阵Padd, 其满足Paddwe的第j位置与第j个加法门的左输入、右输入及输出分别对应相等. 最后P对消息向量we,x,y和z进行加密得到4 个码矩阵Uwe,Ux,Uy,Uz ∈Lm, 记码矩阵U ∈L4m为4 个码矩阵纵向排列后的码矩阵. 需要注意的是, 上述检查矩阵中元素全为常数, 且由于电路结构是公开的, 故检查矩阵可由验证者自行计算得出. (3) 交互阶段.P和V运行如下3 个模块协议:调用模块(1) 检查U与L4m的码距是否小于e.调用模块(2)检查线性约束的正确性,即利用码矩阵Uwe检查w是否满足Paddwe=0.调用模块(2) 和模块(3) 检查二次约束的正确性, 即先调用模块(2) 利用码矩阵Uw,Ux,Uy,Uz检查对于任意的a ∈x,y,z, 有 其用于验证x,y,z是正确构造的, 再调用模块(3) 利用码矩阵Ux,Uy,Uz检查x ⊙y −z?=0,其用于验证x,y,z满足乘法门约束. 可以证明, 协议的可靠性误差为(e+6)/|F|+(1−e/n)t+5((e+2k)/n)t. Ligero++ 指出, 由于在Ligero 中检查码矩阵与谕示多项式一致性的过程相当于验证一个内积关系,即验证对于任意的ξi,i∈[t],p(ξi)?=r·p(ξi),其中r=(r1,r2,··· ,rm),p(ξi)=(p1(ξi),p2(ξi),··· ,pm(ξi)).因此, 可以调用内积论证(出自Virgo[28]) 实现上述检查. 若内积论证中的向量规模为n, 则其通信复杂度为O(logn). 也就是说, 可通过调节m,ℓ进一步降低通信复杂度, 具体描述见讨论总结. 讨论总结. 现分别从底层MPC 协议、零知识性、复杂度和布尔电路版本对上述协议进行讨论分析. (1) 底层MPC 协议. 与ZKBoo、ZKB++ 和KKW18 不同的是, Ligero 系列协议的底层MPC 协议较为简单. 在Ligero 中, 参与者的数目与谕示矩阵的列相等, 且谕示矩阵的每一列即是每个参与方的隐私信息. 由于该MPC 协议的目标联合函数是计算谕示矩阵每一行与某个随机向量的线性组合, 每个参与方的计算任务就是在获取该随机向量后计算持有列与随机向量的线性组合并广播. 该MPC 协议本质上属于客户-服务器模型(client-server model, 见第8.3.5 小节), 基于该MPC 模型, Ligero、Ligero++ 和BooLigero 结合IRS 码实现了通信复杂度亚线性级别的突破;Limbo[49]实现了通信复杂度虽为O(|C|)、但中等规模电路下(少于500 000 个乘法门) 实际通信量最低的NIZKAoK. (2) 零知识性. 上述协议并不是零知识的, 这是因为验证者获取的两种信息可能破坏零知识性, 第一是秘密输入与挑战值的线性组合, 第二是谕示中的t列. 针对第一点, 一个有效的方法是为各谕示矩阵增加一行随机编码且令其不影响原线性组合在ℓ个点的取值, 这保障了线性组合也不会泄露隐私信息. 针对第二点, 基于IRS 码加密消息的随机性, 只需满足验证者可接触的多项式点值数目(获取ℓ个点值以验证电路约束关系、t个点值以验证谕示的一致性) 小于多项式的度大小即可保障零知识性, 即满足k>ℓ+t. 8.3.4 BooLigero BooLigero 由Gvili、Scheffler 和Varia[48]提出, 其优化了Ligero 布尔电路版本的通信复杂度.BooLigero 的协议流程与Ligero 是类似的, 本小节只讨论BooLigero 优化通信复杂度的方法. 主要思路. BooLigero 的主要思路分为四部分, 分别是增加布尔约束、用伽罗瓦域存储比特、利用伽罗瓦域乘法实现按位与和高效比特约束检查协议, 简要描述如下. (1) 增加布尔约束. Ligero 本身虽然是针对算术电路的, 但也可适用于布尔电路. 对于布尔电路, 首先需要为每个电路门值增加布尔约束限制其为0 或1, 即增加约束α2−α=0. 此外还要增加对异或门和与门约束的算术版本. 给定布尔值α1,α2, 考虑约束α1+α2=r0+2·r1, 若规定上述约束中值均为0 或1, 则r0是α1和α2的异或, 则r1是α1和α2的与, 因此可通过增加辅助输入比特d独立验证异或门或与门约束. 例如, 对于与门约束α1·α2=α3, 可增加辅助输入比特d验证线性约束α1+α2?=d+2·α3. 验证异或门的线性约束方法同理可得. 值得注意的是, 为保障可靠性误差足够小, Ligero 中的域往往需取足够大. 但是BooLigero 只需利用域中0 和1 共两个元素, 这会造成约(log2|F|−1) 比特的存储浪费, 并增加通信开销. 一个自然的想法是引入能用一个域元素存储多个布尔值的域, 比如伽罗瓦域, 从而充分利用存储空间. (2) 用伽罗瓦域存储比特. 为解决存储浪费问题, BooLigero 指出可利用伽罗瓦域存储比特值, 从而实现一个域元素存储多个比特. 考虑伽罗瓦域F2γ, 若每一位代表一个比特值, 则一个域元素一次性可以存储γ个比特. 基于此, Ligero 中谕示矩阵的元素数目会降低为原来的1/O(log|F|), 通信复杂度会降低为原来的1/O(log|F|1/2). 然而, 运行Ligero 中的电路约束检查模块不仅需要布尔域到伽罗瓦域的存储转化, 还需要布尔域到伽罗瓦域的电路计算转化, 而这直观上是难以实现的. (4) 高效比特约束检查协议. 在BooLigero 中, 对新变量的约束具有高度规律性, 其形式都是一组向量的“某位置是0” 或者一组向量的“某个位置等于目标向量的某个位置”. 为了验证某变量满足某约束关系, BooLigero 提出了一种零知识的高效比特约束检查协议来实现批量化比特关系验证.该协议基于cut-and-choose 思想, 可以在不揭露秘密输入信息x的同时证明其满足关系T x=0(其中T为某个公开矩阵). 同时, 该协议的通信复杂度仅与安全参数有关, 与隐私信息的长度无关. 讨论总结. 根据电路结构的不同, 相比于Ligero 的布尔电路版本, BooLigero 可将通信复杂度降低为原来的1/O(log|F|1/2)∼1/O(log|F|1/4). 具体的, 若电路全是异或门, 谕示矩阵元素数目会减少至原来的1/O(log|F|), 通信复杂度会降低到原来的1/O(log|F|1/2); 若电路全是与门, 谕示矩阵会因实现伽罗瓦域按位与运算增加至原来变量数的O(log|F|1/2) 倍, 故矩阵元素数目会减少至原来的1/O(log|F|1/2), 通信复杂度会降低至原来的1/O(log|F|1/4). 8.3.5 Limbo Limbo 由Guilhem、Orsini 和Tanguy[49]提出, 其拓展了Ligero 的MPC 协议模型并基于IOP 实现了通信复杂度虽然为O(|C|)、但实际性能良好的NIZKAoK. Limbo 适用于算术电路和布尔电路, 对于布尔电路, Limbo 的实际通信量相比于KKW18 有显著降低; 对于算术电路, 相比于其他基于MPC-inthe-Head 的零知识证明, Limbo 实现了针对中等规模电路(乘法门少于500 000 个) 可满足性问题的当前最优实际性能. 主要思路. 构造基于MPC-in-the-Head 的高效零知识证明的一个自然思路是利用高效的MPC 协议,而这也恰好是KKW18 的主要思路. 与之不同的是, Limbo 的主要思路是利用最适合MPC-in-the-Head的MPC 模型可能会使零知识证明更高效. 具体的, Limbo 中的ρ轮通用MPC 模型如图19 所示, 其是客户-服务器模型(client-server model), 即参与者可分为1 个客户(发送方)PS、n个计算服务器P1,P2,··· ,Pn和1 个接收方PR. 在该模型中,PS拥有整个计算的输入, 且在每一轮的开始阶段PS最多发送1 次消息. 在第j轮(j ∈[2,ρ −1]), 计算服务器调取公共抛币函数获得随机串Rj并根据本轮及之前收到的信息进行本地计算. 在第ρ轮, 计算服务器获得随机串Rρ经过本地计算后向PR发送消息.在上述模型中, 计算服务器之间不需进行交互. 图19 Limbo 的MPC 模型[49](client-server 模型)Figure 19 MPC model of Limbo (client-server model) 上述模型略加修改即可构造基于MPC-in-the-Head 的零知识证明. 此时, 证明者P在脑海中模拟上述MPC 协议的运行, 此时随机串来源于验证者V的随机挑战, 且在每轮结束后P利用本轮发送的信息构造一个谕示. 相比于调用其他MPC 模型, 该证明中计算服务器之间不需交互, 考虑到交互会带来视图规模的增大和运行MPC 协议开销的提升, 因此基于该模型构造的零知识证明的实际通信量和计算开销均较低. 事实上, Ligero 就是ρ= 1 时的特例, 并且该模型本质上属于IOP. 可以证明, 若MPC 协议具有(PR,n −1)-隐私性和(PS,0)-鲁棒性时, 基于该模型的交互式零知识论证可靠性误差为ϵ= 1/n+δ(1−1/n), 其中, (PR,n −1)-隐私性指半诚实模型下敌手腐蚀PR和n −1 个计算服务器仍可保障隐私; (PS,0)-鲁棒性指在恶意模型下敌手腐蚀PS仍可保障鲁棒性,δ为鲁棒性误差并取决于具体MPC 协议. 此外, 将上述MPC 模型中的发送方数目增加为τ个并调用相同的公共抛币函数可将可靠性误差降低为ϵ=1/nτ+δ(1−1/nτ). 底层MPC 协议. 基于上述思路, Limbo 采用一个简单的MPC 协议(见文献[144–146]) 构造了交互式零知识知识论证, 并利用Fiat-Shamir 启发式转换为了NIZKAoK. 对于基于加性秘密分享的MPC协议, 加法门的结果可根据自身的秘密掩藏份额自行计算和更新, 因此只需考虑乘法门. 具体的, 该MPC协议用于证明m个乘法门约束成立, 即证明给定m个三元组{xℓ,yℓ,zℓ}ℓ∈[m], 对于任意的ℓ ∈[m], 都有xℓ·yℓ=zℓ, 该协议的主要思路如协议9 所示. 协议9 Limbo 的底层MPC 协议主要思路[49]公共输入: 域F,ℓ,n, 电路C.证明者秘密输入: {[xℓ]i,[yℓ]i,[zℓ]i}, 其中ℓ ∈[m],i ∈[n], [xℓ]i 表示第i 个计算服务器在第ℓ 个乘法门处左输入的份额, [yℓ]i、[zℓ]i 分别表示在第ℓ 个乘法门处右输入、输出的份额.1. 对于所有的ℓ ∈[m],i ∈[n], 发送方Ps 将份额[xℓ]i,[yℓ]i,[zℓ]i 发送给Pi. 此外, 发送方Ps 随机选取满足关系a·b = c 的向量份额[a]i,[b]i,[c]i 也发送给Pi.2. 各计算服务器调取公共抛币函数获取随机数R,s.3. 对于所有的i ∈[n], 计算服务器Pi 计算[x]i ←([x1]i,R·[x2]i,··· ,Rm−1 ·[xm]i), [y]i ←([y1]i,[y2]i,··· ,[ym]i), [z]i ←∑Rℓ−1 ·[zℓ]i.ℓ∈[m]然后计算服务器Pi 计算[σ]i ←s·[x]i −[a]i 和[ρ]i ←[y]i −[b]i, 随后广播[σ]i 和[ρ]i.4. 各计算服务器恢复σ 和ρ.5. 对于所有的i ∈[n], 计算服务器Pi 计算[v]i ←s·[z]i −[c]i −[b]i ·σ −[a]i ·ρ −ρ·σ.然后Pi 将[v]i 发送给接收方PR.6. PR 恢复v.输出: 比特b, 若v = 0, 输出b = 1; 否则输出b = 0. 现分析该MPC 协议的可靠性. 若至少一个乘法门三元组是错误的, 则由Schwartz-Zippel 引理和R的随机性可知, 若[x]i·[y]i −[z]i ̸=0, 则验证者通过的概率为(m −1)/|F|. 基于此, 如果[x]i·[y]i −[z]i和[a]·[b]−[c] 至少有一个不为0, 由s的随机性可知, 验证者通过的概率为2/|F|. 因此, 该协议的可靠性为(m −1)/|F|+(1−(m −1)/|F|)·2/|F|. 利用上述MPC 协议可自然构造对应的零知识证明, 此时协议轮数为3. 然而在上述MPC 协议中, 广播的消息规模为2mn, 因此对应零知识证明的通信复杂度至少为O(n|CM|). 为进一步降低通信复杂度,Guilhem、Orsini 和Tanguy 提出了一种通过压缩内积规模降低通信复杂度的方法, 不过其会增加logk m轮交互. 利用该方法, 对于每个乘法门, 只需传输1 个域元素即可完成证明, 此时协议的通信复杂度可降低为O(|C|). 讨论总结. 基于client-server 模型和IOP,Limbo 实现了针对中等规模算术电路(乘法门少于500 000个) 可满足性问题的良好实际性能. 除此之外, 与Ligero 类似, Limbo 也具有一定的灵活性(flexibility).例如, 在相同的目标可靠性误差下, 增加n的数目可有效降低轮数从而降低实际通信量, 然而这会增加证明者的计算开销, 因此可通过调节n,τ等参数的大小从而调节证明者计算开销和通信量之间的关系. 基于MPC-in-the-Head 的零知识证明具有以下优点: (1) 底层难题假设更为通用. 该类证明只需假设CRHF 存在, 且仅有对称密钥操作, 故是抗量子的,并可用于构造高效抗量子数字签名(如Picnic[34,47,49]6https://microsoft.github.io/Picnic). (2) 具有一定的灵活性. 可通过调整参数控制证明者的计算开销和通信量之间的关系. (3) 可堆叠性(stackable). Goel 等人[148]指出Ligero 和KKW18 具有可堆叠性, 即给定某个针对NP 语言L(R) 的Σ 协议, 证明陈述(x1∈L(R))∨x2∈L(R))∨···∨(xℓ ∈L(R)) 的通信复杂度可为O(CC(Σ)+λlogℓ), 其中CC(Σ) 为Σ 协议的通信复杂度,λ为安全参数, 而证明上述陈述的平凡通信复杂度为O(ℓ·CC(Σ)+λ). 然而, 该类协议的通信复杂度虽已达到对数级别, 但是实际通信量通常较高[27, §9.2], 如何进一步降低该类零知识证明的实际通信量是存在的一个问题. 此外, 目前在理论研究和实际性能层面均未找到最适合MPC-in-the-Head 的MPC 协议, 因此, 如何选取高效的MPC 协议是可能是未来的一个研究方向. 近年来, 虽然针对简洁非交互零知识证明的研究取得了较大进展, 并且简洁非交互零知识证明逐渐在区块链、隐私计算等领域得到了较为广泛的应用, 但是仍然存在很多尚未解决的理论和技术问题. 以下列出未来的主要发展趋势. (1) 通用构造方法层面. 进一步总结完善构造简洁非交互零知识证明的通用构造方法, 如拓宽IPCP、IOP, 探讨是否存在可用于更高效构造简洁非交互零知识证明的信息论安全证明, 讨论基于IPA的零知识证明能否也存在底层信息论安全证明等; 基于某一特定信息论安全证明, 优化改进密码编译器的具体技术, 实现更好的性能. (2) 性能层面. 从复杂度角度, 进一步降低简洁非交互零知识的证明、通信和验证复杂度, 如削弱基于DEIP 的零知识证明中电路深度d的影响; 从实际性能角度, 优化算法性能, 如利用批量验证的方式降低基于IPA 的零知识证明的实际验证开销、通过证明者在脑海中一次性模拟多个MPC 运行的方式降低基于MPC-in-the-Head 的零知识证明的实际证明开销、选取或设计更适合MPC-in-the-Head 的MPC 协议等. (3) 初始化层面. 虽然基于QAP 的零知识证明(zk-SNARK) 可实现常数级别群元素的通信复杂度和仅与公共输入输出长度成线性关系的验证复杂度, 但在区块链应用中, 如何保障可信初始化的安全、优化可信初始化的性能仍是目前的一个难点. 因此, 探讨高效可更新CRS 的构造方式, 研究CRS 长度更短、生成更快的zk-SNARK 是未来一个可能的发展方向. (4) 安全层面. 研究基于标准假设如何构造简洁非交互零知识证明, 提高协议的安全性; 基于更为通用的难题假设构造zk-SNARK 及系列可更新零知识证明; 探讨在系统参数可公开生成的零知识证明中利用基于ROM 的Fiat-Shamir 启发式实现非交互是否及会如何降低协议性能.





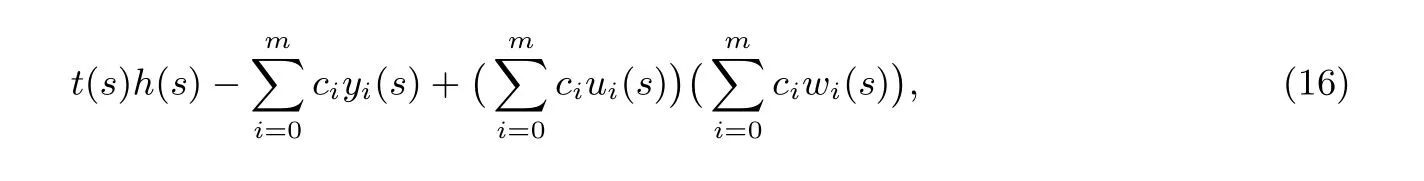

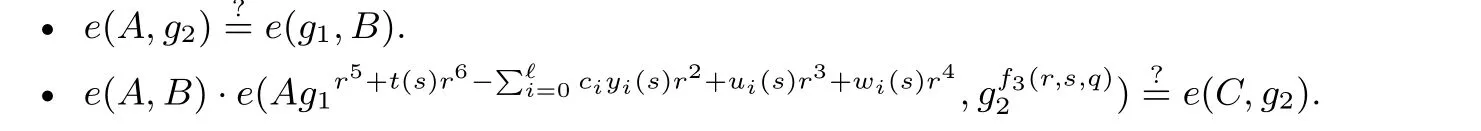
5.4 总结
6 基于DEIP 的零知识证明
6.1 定义及概念

6.2 背景及主要思路

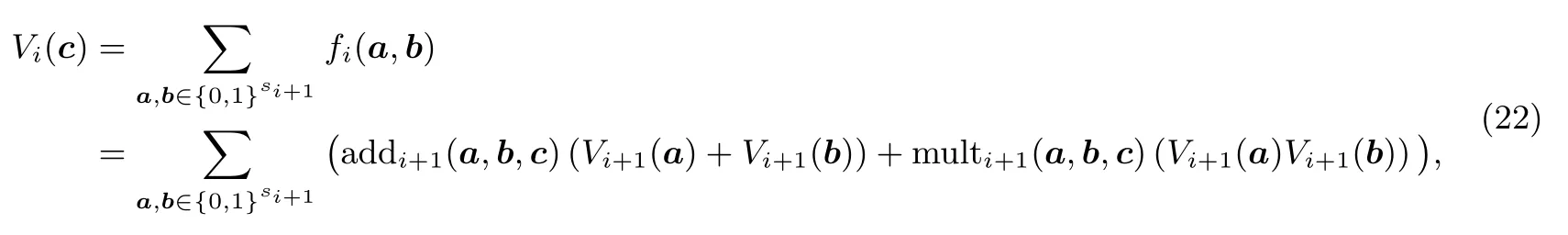







6.3 典型协议分析
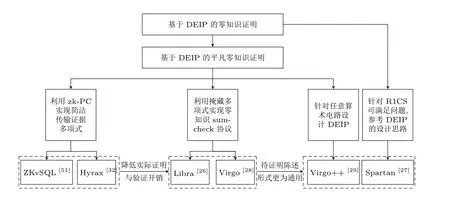





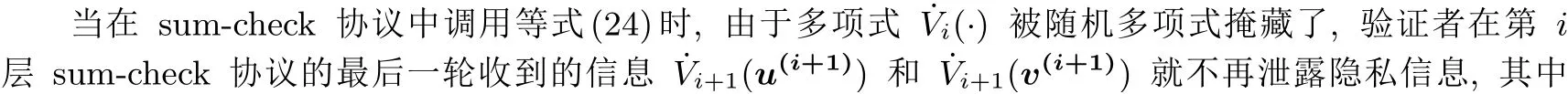






6.4 总结
7 基于IPA 的零知识证明
7.1 定义及概念

7.2 背景及主要思路
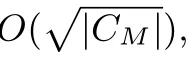






7.3 典型协议分析








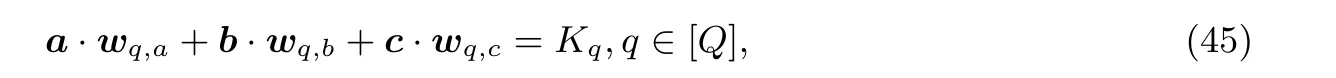
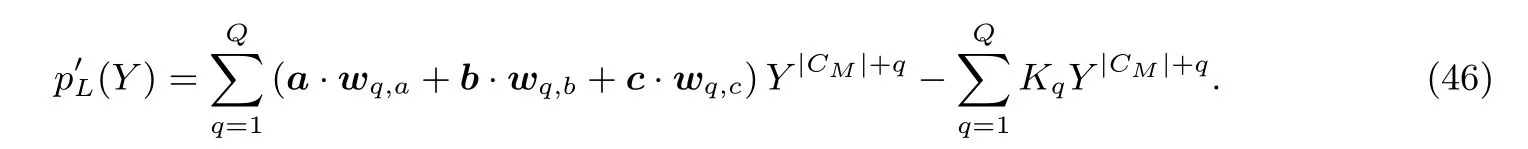



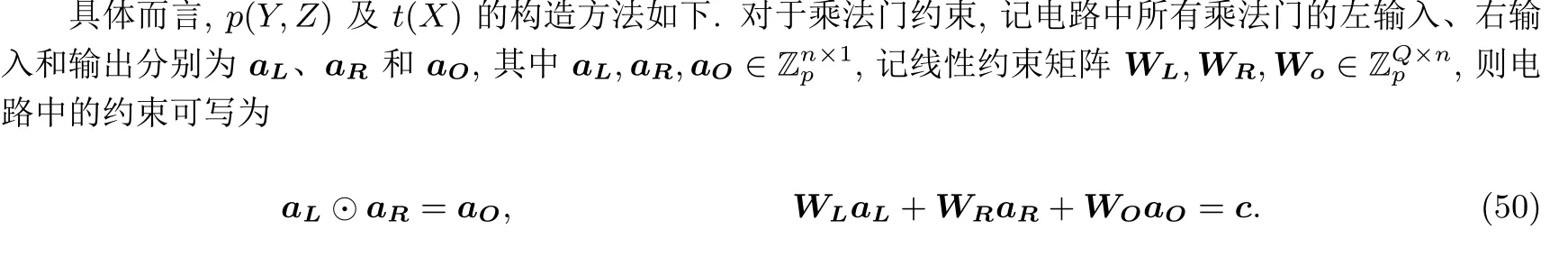




7.4 总结
8 基于MPC-in-the-Head 的零知识证明
8.1 定义及概念

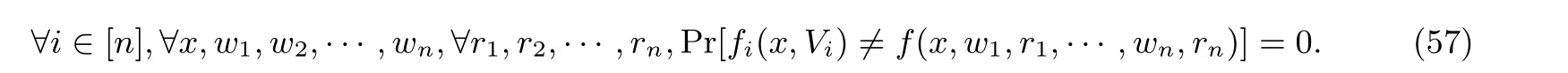

8.2 背景及主要思路




8.3 典型协议分析


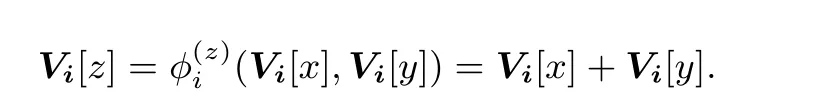
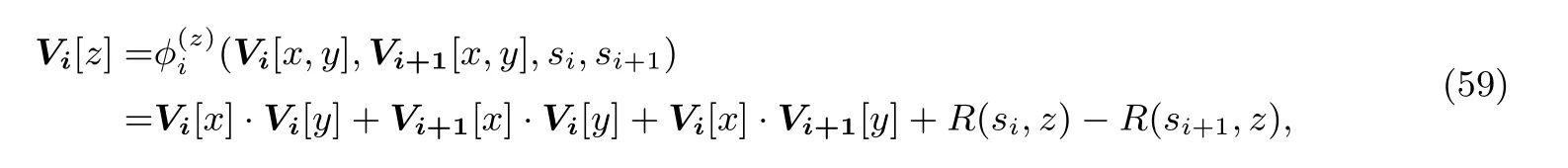


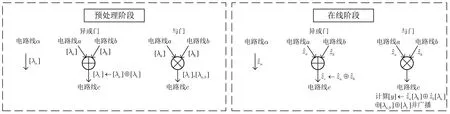


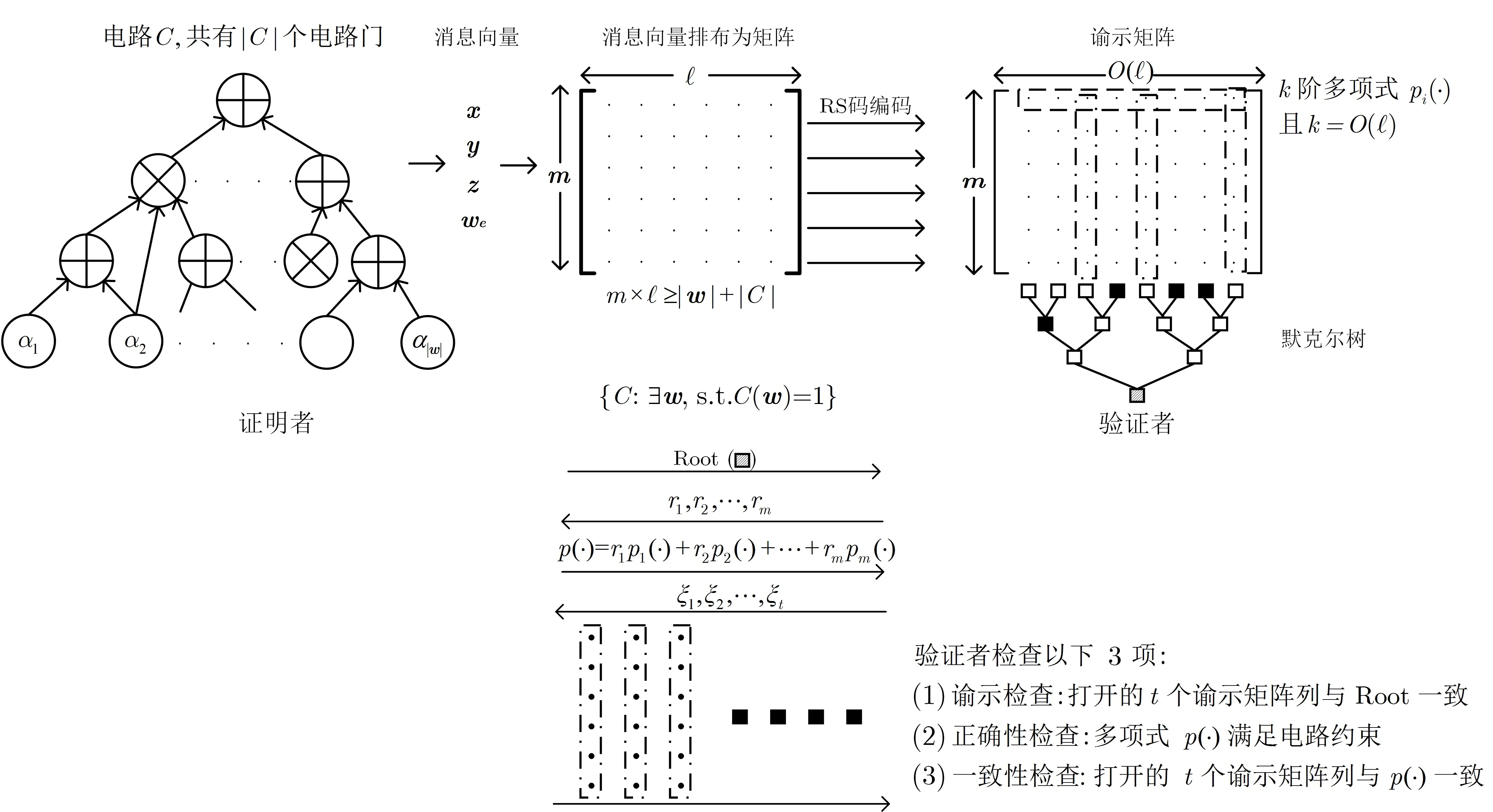
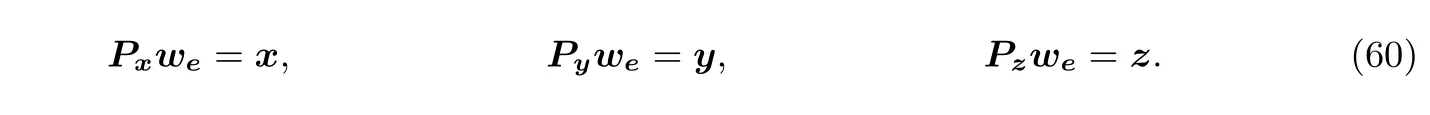





8.4 总结
9 未来研究方向

