多自由度系统对简谐激振力响应的仿真分析

景帅 罗宇杰 曹宇博 赵梓旭 施佳晨

摘 要：实际工程结构中大多数均为多自由度体系，尽管其分析与二自由度系统振动分析并没有本质区别，但随着自由度数量的增多，分析步骤也越来越繁琐。计算机技术和有限元技术的快速发展，使许多大规模复杂结构在任意激励下的动态响应求解也更加可行。本篇首先阐述了解决多自由度系统响应问题的多种方式，介绍其优缺点与适用性，最后对振型叠加法展开了重点研究并展示运算流程。考虑到矩阵法形式简单运算统一，故采用这一数学工具进行求解，具体过程包括建立多自由度系统振动微分方程、确定固有频率与主振型、引入主坐标及正则坐标以及确定系统响应。MATLAB软件的变量对象皆为矩阵且具有强大的算力并可直接输出响应曲线，因此使用该软件进行计算。

关键词：简谐激振力;振型叠加法;仿真

1 引言

一般来说工程中的实际问题所处理的机械系统均为多自由度振动系统，因为其复杂性通常需要采用连续模型才能加以进行描述，其所涉及的振动分析理论与偏微分方程理论也是十分复杂。很多情况下可经过一定的抽象过程将其简化为有限多个自由度系统来进行研究。目前主流求解方法分为两类即直接积分法与间接积分法，这两类方法都有各自的优势以及局限性。因此对待以上问题需要采用有效的求解方法，兼顾效率与成本。下面介绍求解系统振动响应的几种方法及其各自的优缺点和适用范围。

1.1 直接积分法求解

直接积分法其基本原理是在一定时间范围内对系统所响应的时间历程进行离散，将系统运动微分方程分解为各离散时间的运动微分方程，并确定在某个时间的运动位置、速度和加速度的近似表达式，再将表达式代入系统运动方程中，对相互耦合的系统振动方程进行逐步积分求解。直接积分法原理简单概念清晰，不需要对振动方程进行简化处理，只需输入阻尼矩阵、质量矩阵、刚度矩阵等参数即可进行求解。该方法虽然操作简单且精确度高，但是计算时间过长、效率过低且相比其他方法会占用大量的计算机资源，因此使用频率并不高。

1.2 缩聚法求解

对复杂结构的系统进行动响应分析时，离散构造的自由度数目多、运算量过大。因此在确保一定计算精度的条件下，可以运用缩减技术对模型进行缩聚处理。该方法旨在通过适当的变换处理消除对系统整体振动响应影响微弱的自由度，以此来达到降低自由度、简化计算量、提高效率的目的。缩聚法求解的局限在于如何寻找对系统影响微弱的自由度，自由度选择错误则会大大地影响分析求解的精度。

1.3 振型叠加法求解

振型叠加法采用模态变换对原自由度系统的运动方程解耦得到非耦合的n个单自由度系统的运动方程。模态变换以求解广义特征值问题为代价，对系统固有特性没有影响，通过对n个单自由度系统运动方程积分，对比联立方程组的直接积分更加节省时间。振型叠加法只适用于线性、时不变系统。对于激励的高频成分很微弱或者系统的高频振动没有激发出来等情况，系统的响应中只有较低的几阶振型分量，因此使用振型叠加法可以大幅度简化计算量。

2 多自由度振动系统仿真模型的建立

多自由度振动系统的动力学模型如图一所示。

4 仿真分析

如果给定多自由度系统（如图1所示且不记阻尼）的参数以及简谐激振力函数表达式，就可以利用下列程序得出系统的响应。设 ， ，振动位移为 、 和 ，并在质量 上作用激振力 ，其中 。

程序代码如下：

clc;clear;

n=3;m1=1;m2=1;m3=1;k1=10000;k2=10000;k3=10000;k4=10000;

t=0：0.001：0.049;F1=0;F2=0;F3=10;F=[F1;F2;F3];p=125; f=F.*sin（p*t）;

M=[m1 0 0;0 m2 0;0 0 m3];

K=[k1+k2 -k2 0;-k2 k2+k3 -k3; 0 -k3 k3];D=inv（M）*K;[A lam]=eig（D）;

for i=1：n w（i）=sqrt（lam（i，i））; end w;

AF=[0 0 0;A;0 0 0];z=[0 0 0 0 0];plot（AF） hold on

ylabel（{'主振型振幅'}）;xlabel（{'距固定点距离'}）;plot（z）

for i=1：n Mzhu（i）=A（：，（i））'*M*A（：，（i））; end Mzhu;

for i=1：n Azhu（：，i）=A（：，（i））.*（Mzhu（i））^（-1/2）; end Azhu; Fzhu=Azhu'*F

for i=1：n Xzhu（i）=Fzhu（i）/（（w（i））^2-125^2） end

Xzhu; X0=Azhu*Xzhu'; X=X0.*sin（p*t）;

subplot（411），plot（t（1：50），f） ，grid;subplot（412），plot（t（1：50），X（1，：）） ，grid

subplot（413），plot（t（1：50），X（2，：）） ，grid;subplot（414），plot（t（1：50），X（3，：）） ，grid

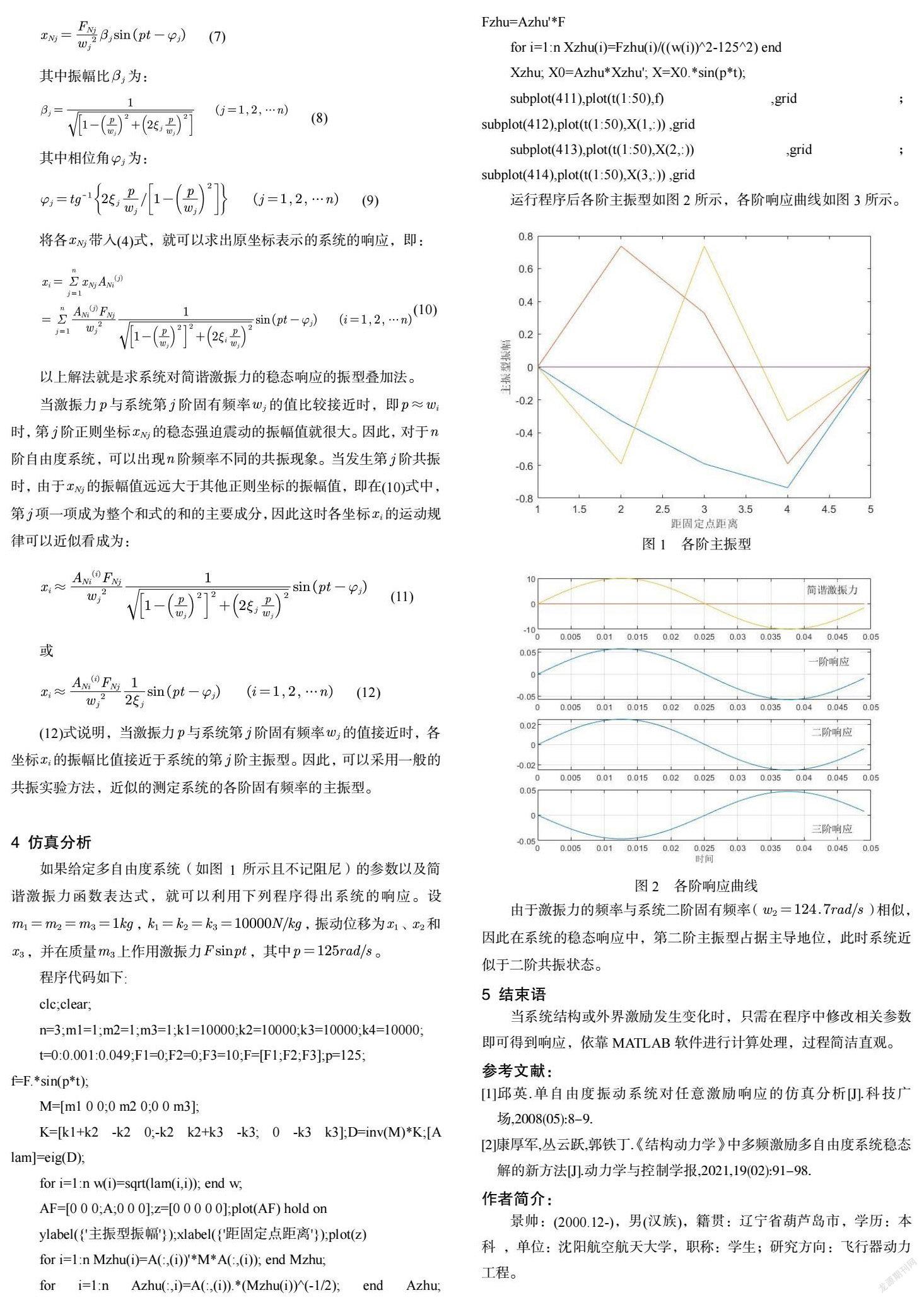
运行程序后各阶主振型如图2所示，各阶响应曲线如图3所示。

由于激振力的频率与系统二阶固有频率（ ）相似，因此在系统的稳态响应中，第二阶主振型占据主导地位，此时系统近似于二阶共振状态。

5 结束语

当系统结构或外界激励发生变化时，只需在程序中修改相关参数即可得到响应，依靠MATLAB軟件进行计算处理，过程简洁直观。

参考文献：

[1]邱英.单自由度振动系统对任意激励响应的仿真分析[J].科技广场，2008（05）：8-9.

[2]康厚军，丛云跃，郭铁丁.《结构动力学》中多频激励多自由度系统稳态解的新方法[J].动力学与控制学报，2021，19（02）：91-98.

作者简介：

景帅：（2000.12-），男（汉族），籍贯：辽宁省葫芦岛市，学历：本科 ，单位：沈阳航空航天大学，职称：学生;研究方向：飞行器动力工程。