基于仿生优化算法的聚类改进算法
覃承友, 谢晓兰, 王悦悦, 郭 杨
(桂林理工大学 a.广西嵌入式技术与智能系统重点实验室; b.信息科学与工程学院, 广西 桂林 541006)
聚类, 是数据挖掘中一个重要的组成部分, 其目的为按照设定的特定标准把物理或抽象的对象集合分割成不同类或簇的小集合, 这些小集合中的对象彼此相似, 并与其他类或簇的对象有所差异, 即聚类产生的同一类数据对象尽可能聚合在一起, 不同的数据对象尽可能分离[1]。k均值聚类算法(k-means clustering algorithm, 简称k-means)在聚类算法中有着举足轻重的地位, 虽然其逻辑理论简单、可高效实现, 应用十分广泛, 在故障检测[2]、无人机应急[3]、隐私保护[4]等方面都有着广泛的应用,但是k-means算法本身也存在着一定缺陷, 如对初始聚类中心非常敏感, 且在迭代过程中容易陷入局部最优等问题。针对这些问题, 对于k-means算法的改进方法有很多, 其中仿生优化算法作为当今研究的热门领域, 和k-means进行结合使用是一个可行的方法, 其模拟了昆虫、兽群、鸟群和鱼群等群体的行为, 群体中每个成员通过学习自身和其他成员的经验不断优化搜索, 可以有效地找出全局最优解。如在文献[5]中提出了基于改进人工蜂群算法的k均值聚类算法, 使用最大最小距离初始化蜂群, 构造出一种基于全局引导的位置更新策略, 提高了迭代寻优的效率; 文献[6]提出了基于改进粒子群算法的k均值聚类算法, 使用加入混沌搜索过程的粒子群算法增加粒子的多样性, 为k-means有效地找到了较好的初始中心; 文献[7]提出了基于云计算平台的仿生优化聚类数据挖掘算法, 通过利用相似聚类和狼群优化算法, 以头狼的位置确定聚类中心, 在不断的狼群优化以及相似聚类中实现了在云计算平台对数据样本大且高维的数据聚类, 并提升了收敛速度。上述算法在改进k-means中侧重点各有不同, 对于k-means对初始聚类中心的敏感和易陷入局部最优的问题并没有得到很好的解决或达到很好的聚类效果。
本文在研究k-means聚类算法及仿生优化算法上, 将属于仿生优化算法中的果蝇优化算法(fruit fly optimization algorithm, FOA)与k-means进行结合以达到更好的聚类效果。用改进的果蝇优化算法改良k-means的聚类中心, 解决k-means易陷入局部最优及其初始聚类中心敏感的问题。考虑到不同算法模型在不同数据集上的效果有所差异, 为了实验的严谨以及准确性, 本方法选择不同UCI的标准数据集进行实验对比分析。
1 相关算法
1.1 k-means聚类算法
对于给定数据集X=(X1,X2,…,Xn)其中包含n个成员对象,k-means的任务就是将这n个对象根据某种距离或某种相似性划分到k个簇中(C1,C2, …,Ck, 2≤k≤n), 簇的聚类中心称为质心, 并使得这k个簇的聚类均值达到总体误差最小, 即损失函数达到最小,k-means的损失函数为
(1)
其中:x表示数据样本点;Ci表示第i个簇;k表示划分的簇数;φi为簇Ci的质心, 表示为
(2)
算法的具体步骤为:
步骤1: 给定需要聚类产生的簇数k, 在数据集中随机抽取k个点作为初始质心, 给定迭代次数和聚类效果阈值。
步骤2: 按照式(3)计算给定数据集中所有对象与各个质心的欧氏距离
(3)
其中:dist(x,y)表示每个对象的欧氏距离;xi、yi表示对象的坐标;n表示每个簇中的对象总数。
步骤3: 根据簇中所有的对象, 根据式(2)重新计算质心。
步骤 4: 判断是否达到迭代次数或满足聚类效果阈值, 若是, 停止算法, 保存质心与各个聚类的对象; 若否, 重复步骤2、3和4。
1.2 果蝇优化算法
果蝇优化算法[8]的核心在于果蝇个体利用自身的嗅觉获取食物源的浓度值, 并向周围的其他果蝇个体发送气味信息, 再利用视觉飞向浓度值最高的果蝇位置, 飞行的半径取决于食物源的浓度值大小。标准的果蝇优化算法流程如下[9-10]。
步骤1:初始种群规模sizepop, 最大迭代次数maxgen, 维度dim和果蝇个体的飞行半径L, 并初始化果蝇种群的位置, 其对应的初始位置信息定义为
(4)
步骤2:每一个果蝇个体根据赋予的飞行半径和方向, 开始更新自身的位置, 更新公式如下
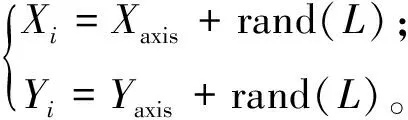
(5)
步骤3:由于初始食物源的方向和距离是未知的, 因此每一个果蝇个体根据式(6)计算距离原点的距离dist, 并根据式(7)作为其对于食物源的浓度值判定Si, 同时利用式(8)计算每一个果蝇个体的味道浓度值Smelli
(6)
Si=1/disti;
(7)
Smelli=fitness(Si)。
(8)
式中:Xaxis、Yaxis表示初始种群坐标; rand()表示随机分布数;Xi、Yi为更新坐标;i表示第i个果蝇个体; fitness()表示味道浓度值的判断函数, 即适应度函数。
步骤4:记录当前群体中最优味道浓度值的果蝇位置信息, 并将其具体信息存入最优群体Smellbest。
步骤5: 根据最优味道浓度值和记录的位置信息bestSmell,果蝇群体的所有个体都往这个方向飞去。
步骤6:判断是否达到迭代次数maxgen, 否, 则重复步骤2~6;是, 则输出最优值, 结束循环。
通过以上迭代步骤可知, FOA的搜索策略是基于全局搜索的, 并根据每次迭代的最优解指导下一次迭代的方向与位置, 能够使种群以当前最优解继续开展随机搜索, 从而朝着更优的方向搜索前进。
2 基于果蝇优化算法的k-means算法
2.1 基于F分布的果蝇飞行半径更新策略
F分布式是一种非对称分布[11], 其有两个自由度, 且位置不可置换, 设X服从自由度为n1的卡方分布,Y服从自由度为n2的卡方分布, 且X、Y独立, 则称随机变量F=(X/n1)/(Y/n2)服从自由度为(n1,n2)的F分布记为F~F(n1,n2), 其概率密度表达式为
(9)

(10)
其中:n1为第一自由度;n2为第二自由度。对于自由度不同的F分布如图1所示。

图1 不同自由度的F分布曲线对比
使用基于F分布的果蝇飞行半径更新策略能有效优化果蝇优化算法中的飞行机制。在原始的果蝇优化算法中, 每次的飞行半径是固定的, 这就影响了算法在迭代中的寻优能力:如设置过大的飞行半径,虽然在算法迭代前期能很好地扩大搜索范围, 并有效避免陷入局部最优, 但是在算法迭代后期却容易在最优解附近产生震荡, 难以有效接近最优解; 若设置过小的飞行半径,则容易在算法迭代前期过早的陷入局部最优, 难以搜索最优解。因此,选择一个合适的飞行半径对于果蝇优化算法十分重要, 使用本文基于F分布的飞行半径, 能有效规避以上两个问题。由图1可知, 在F分布的曲线中, 概率密度的变化曲线是非对称的, 算法设置每迭代一次,F分布的自变量x增加0.05, 其对应的概率密度即为算法变化步长。以基于F分布的变化飞行半径, 算法能在开始迭代的时候能很好地扩大搜索范围, 迭代到最后能避免震荡并找到全局最优解, 有效提升果蝇优化算法的寻优效率。
2.2 基于精英保留机制的果蝇种群优化
精英保留机制, 是一种高效的全局搜索机制, 近年来在仿生优化算法的改进中运用十分广泛, 其主要思想是针对一个问题求出所有可行解, 通过可行解求出反向解, 并对原解和反向解进行评估比较, 从而选择较优的解作为精英解保留为下一代。
反向解的求解取决于反向点, 设有n个二维空间点的集合S=(S1,S2, …,Sn),Sa和Sb为集合的最大值和最小值, 则对于点Si的反向点定义为Si′, 其表达式为
Si′=Sa+Sb-Si。
(11)
通过比较原始解和反向解, 选择其中的最优解作为精英解。设点Si为果蝇的原始解, 则Si′为反向解, 设f(S)为目标函数, 当f(Si)≥f(Si′)时, 称为Si精英解; 当f(Si) 由于精英解是比较原始解和反向解得来的, 因此能及时避免对劣质果蝇个体的继续搜索, 让种群向着更优的区域搜索。使用精英解对果蝇种群的改进, 能有效扩大种群的搜索范围, 避免陷入局部最优。 本文基于以上两点改进策略提出了基于改进果蝇优化算法的k-means聚类算法BFOA-K。该算法的基本思想是:通过改进的果蝇优化算法进行一次迭代搜索最优值, 将得到的最优值的位置信息作为k-means聚类的初始质心并开始一次聚类分析, 再利用聚类得到新的质心, 将新的质心的位置信息返回更新果蝇种群, 反复交替迭代执行FOA和k-means直到满足最大迭代次数结束算法。改进的BFOA-K算法的流程如下: 步骤 1:初始果蝇种群规模sizepop, 维度dim最大迭代次数maxgen, 利用F分布定义果蝇飞行半径L和初始化果蝇种群的位置, 并给定聚类的簇数k。 步骤2: 利用式(11)重新定义果蝇个体的位置信息, 比较它们的最优值来定义精英群体, 同时每一个果蝇个体根据赋予的飞行半径和方向, 开始更新自身的位置。 步骤3: 由于初始食物源的方向和距离是未知的, 因此先计算每一个果蝇个体距离原点的距离dist, 并根据式(7)作为其对于食物源的浓度值判定Si, 根据式(8)计算每一个果蝇个体的味道浓度值Smelli。 步骤 4: 记录当前群体中最优味道浓度值的果蝇位置信息, 并将其具体信息存入最优群体Smellbest。 步骤5:根据记录的最优个体的位置信息bestSmell, 将其作为聚类的初始质心, 并执行如下操作: a.根据欧氏距离利用式(3)计算数据集中每个对象所隶属的质心; b.根据分配的簇中的对象, 根据式(2)重新计算每个簇的质心; 记录每个质心的位置信息和聚类结果, 并将质心位置重新作为果蝇种群的个体, 根据最优味道浓度值和记录的位置信息, 果蝇群体的每一个个体都往这个方向飞去。 步骤6: 判断是否达到迭代次数maxgen。否, 重复步骤2~6;是, 则输出最优值, 结束循环。 本文的算法流程如图2所示。 图2 本文算法流程图 为了验证本文算法的有效性, 使用4组算法实验作为对比, 分别为传统k-means聚类算法[12]、IABC算法[5]、基于自适应参数改进的密度聚类算法KANN-DBSCAN[13]、无改进果蝇优化k-means聚类算法FOA-K和本文提出的基于改进果蝇优化算法的k-means聚类算法BFOA-K。为了验证算法的多样性, 将采用多组数据集进行实验, 数据集采用UCI上的Iris、Wine、WDBC和Yeast 4个标准数据集。本文实验环境为Windows 10 操作系统, CPU参数为Xeon(R)E-2124G@3.40 GHz, 16 GB内存, Matlab R2018b, Python 3.7。各个数据集的详细信息见表1。 表1 各数据集详细信息 聚类的目的是将特征属性相近的划分成同一个簇, 在聚类划分簇中有很多的评价指标, 本文评价指标采用调整兰德指数(ARI)衡量数据分布的吻合程度 (12) 其中:RI表示兰德指数; E(RI)表示兰德指数的期望; max(RI)表示最大兰德指数。 采用聚类精确度(ACC)比较获得标签和数据提供的真实标签 ACC=NAC/N, (13) 其中:N表示样本总数;NAC表示聚类正确的数量。 采用标准化互信息(NMI)度量聚类结果的相近程度 (14) 其中:U表示真实标签向量;V表示预测标签向量;MI(U,V)表示互信息;H(U)和H(V)表示信息熵。 由于4个数据集的属性各不相同, 因此在选择F分布的自由度时也不同, Iris、Wine、WDBC和Yeast选择的F分布的自由度依次是(5, 5)、(10, 5)、(5, 50)和(10, 50), 算法对比将在每个数据集上重复运行100次, 计算每个评价指标的平均值。上述评价指标设置为值越大表示效果越好。实验结果如表2~表5所示。 表2 5种算法在Iris数据集上的比较 表3 5种算法在Wine数据集上的比较 表4 5种算法在WDBC数据集上的比较 表5 5种算法在Yeast数据集上的比较 在4个数据集的测试中, 加入改进果蝇优化算法的k-means聚类算法在各方面都能达到更好的聚类效果。BFOA-K相较于传统k-means算法,ARI平均提升了20.81%,ACC平均提升了23.56%,NMI平均提升了29.75%, 较于其他对比算法平均也有12.67%的提升。在样本数量及属性数不大的情况下, 5种算法在各种评价指标下都有很好的聚类效果, 但总体还是本文提出的算法要优于其他对比算法; 而当样本数量及属性数增加时, 5种算法的性能都有所下降, 但本文算法还是稍微优于其他对比算法, 其主要原因是BFOA-K算法不仅在果蝇飞行半径上使用了可变的F分布, 动态调整果蝇搜索半径, 而且在果蝇的种群优化上使用了精英策略, 使得果蝇扩大了搜索范围, 增加了果蝇的多样性。但是在高维度和高样本量的数据集中, 尤其是在Yeast数据集下每个算法表现都不好, 这主要是因为涉及高维高样本的数据集中需要进行一定的降维或特征提取, 所以会丢失一定的信息量, 导致聚类效果不明显, 改进数据集降维方法将是以后的研究重点。 为了验证本文算法的收敛速度及收敛程度, 选取了样本属性都有一定差异的Iris和Yeast两个数据集进行比较, 两个数据集随迭代次数的目标函数适应值变化曲线如图3、图4所示。 图3 5种算法在Iris数据集迭代图 图4 5种算法在Yeast数据集迭代图 可以看出,本文提出的BFOA-K算法在两个数据集的测试中, 收敛速度和程度都优于传统k-means聚类算法;尽管IABC算法在Iris数据集的迭代过程有更好的适应度, 因BFOA-K在聚类过程中注重的是聚类效果和收敛速度的平衡, 所以BFOA-K的聚类效果与IABC差距并不大, 且BFOA-K的收敛速度明显快于IABC。在样本数量和属性数均不多的Iris数据集中, 5个算法的性能都极为相近, 但是加入F分布变化步长的BFOA-K在改变飞行半径的情况下, 收敛速度和收敛程度都略优于其他算法。而在样本数量和属性数与Iris数据集差异明显的Yeast数据集的测试中, 无论是收敛速度还是收敛程度, BFOA-K的目标函数适应值都要优于其他算法, 这主要得益于精英策略对果蝇种群搜索范围的优化和F分布的飞行半径的双重影响。在样本数量不高和维度较低的数据集中,F分布能发挥大部分的作用, 在高维高数据样本的数据集中, 两个改进策略则能共同发挥作用, 改善聚类效果。通过Iris和Yeast两个数据集的对比实验, 证明了本文算法能在不同数据集上在更短的时间内拥有更好的聚类效果, 证明了算法性能的有效性。 本文针对k-means聚类算法对于初始质心的敏感和容易陷入局部最优的问题, 提出了基于改进果蝇优化算法的k-means算法(BFOA-K)。通过分析k-means算法和FOA算法的特点, 在融合算法的同时改进了FOA, 通过加入F分布, 利用其特性作为动态调整果蝇的飞行半径; 利用精英果蝇, 拓展了果蝇的搜索范围;利用种群的多样性提升了算法的稳定性。采用4个UCI的标准数据集进行仿真实验, 将本文算法与多种算法进行比较, 结果显示, 在各个评价指标中本文提出的算法都有良好的聚类效果, 证明了算法的有效性,并用两个对比数据集进行测试, 结果表明无论在收敛速度还是收敛程度本文的BFOA-K算法都有着优异的表现, 有效证明了算法的稳定性。 本文算法在针对高维和高数据样本的数据集中聚类效果没有体现出明显的优异性, 今后需要结合其他改进策略, 对算法进行更进一步的研究, 得到更加完善的结果。2.3 改进的k-means算法

3 仿真结果及分析
3.1 实验分析

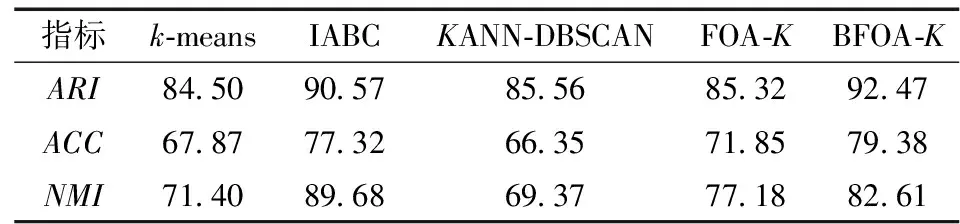
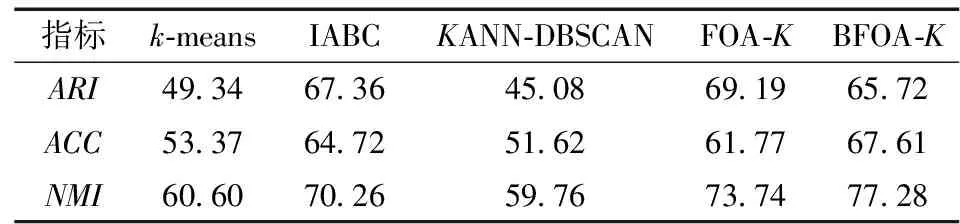
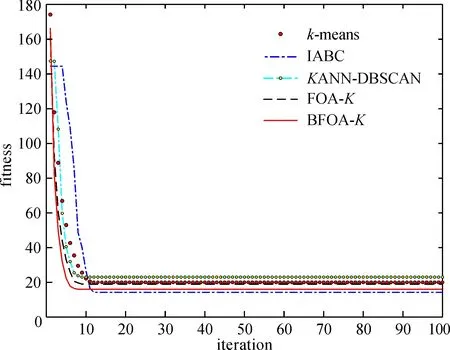
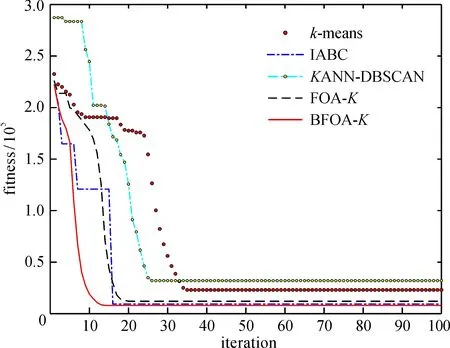
3.2 结果与分析


4 结束语

